基于BP神经网络EPS系统控制策略研究

商显赫，林幕义，2，陈 勇，2，马 彬

（1.北京信息科技大学机电工程学院，北京100192；2.北京电动车辆协同创新中心，北京100192）

1 引言

电动助力转向（Electric Power Steering）系统具有能耗低、可靠性高、维修方便等优点，因此在汽车上得到迅速的普及和应用，由于人们不断追求更高舒适性的驾驶体验，所以希望EPS系统能够满足转向驾驶要求，比如驾驶员在转向时希望省力还要有路感，针对这个问题，许多研究者对助力特性深入探究，但是大多集中在驾驶员操纵方向盘的力矩与电机助力上，很少有人研究车速与助力的关系，文献[1]借助ADAMS∕CAR软件进行建模和仿真，找到了车速与EPS系统助力矩之间的关系，确定了微型客车的车速感应系数，但是却忽略了悬架、轮胎等汽车部件的影响。

因此，利用Carsim软件接近实车的模型的优点，然后结合中国驾驶员所偏好的转向力矩，确定了目标车型的车速感应系数，然后通过曲线拟合的方式，设计了曲线型助力特性曲线；接着利用神经网络可以无限接近任意非线性函数的能力，于是采用基于BP神经网络的PID自适应控制，完成k p、k i、k d三个参数的自整定，避免了调整参数的繁琐和工作性能不佳的缺点，最后通过Matlab∕Simulink和Carsim的联合仿真试验，验证了车速感应系数获得的合理性，基于BP神经网络控制策略比传统的PID控制策略具有更高的鲁棒性，为转向控制器的设计提供了参考。

2 电动助力特性曲线的设计

助力特性的目标电流值，在转向回正时是不起作用的，只有在常规的转向助力模式下有效，助力特性曲线的类型，也会影响驾驶性能，不能按照简单的计算方法去选择，而是要根据符合中国驾驶员的驾驶习惯，按照对转向系统的要求进行设计，其中曲线型助力特性曲线可以平衡要求转向轻便性与具备驾驶路感的问题，故采用并进行拟合设计。

等式（1）给出了曲线辅助特性曲线的工作范围，变量是方向盘扭矩，当绝对值小于1N·m时，助力电机无扭矩输出，当绝对值大于6N·m时，电机的工作状态是提供最大输出，当在区间(1∼6)N·m时，助力扭矩值由K(v)×f(T d)的值确定。

式中：T dmax、T h0—电机工作时的门限值；K(v)—车速感应系数；f(T d)—方向盘力矩函数[2-3]。

2.1 车速感应系数的设计

由于汽车在不同车速行驶时的阻力矩是非线性变化的，为了克服转向过程中的阻力矩，故用车速感应系数来表征车速与助力矩之间的关系，由式（1）可知，电机理想助力矩T a_exp是决定车速感应系数的主要因素，因此，要确定某一车速下的感应系数，需要首先确定该车速下的理想助力矩，式（2）给出了汽车未装有EPS时的方向盘最大转矩T hmax、电机理想助力矩T a_exp和汽车装有EPS时的方向盘理想转矩T d_exp之间相互影响的关系。

为了在速度差异不同的情况下探索方向盘的理想转矩，文献[4]指出了中国驾驶员首选的转向力矩，跟欧洲、日本等地驾驶者钟爱的理想转矩相同，在线性区域内，随车速的增大逐渐增大，因此为路感模拟提供了理论依据，为助力特性曲线的设计提供参考，另外，文献[5]指出一定转向盘转角或者侧向加速度下，理想转向盘转矩与速度近似成线性正比关系，并且在特定情况下，与汽车的类型无关。

基于学者的研究成果，得到方向盘理想转矩的大小；对于汽车未装有EPS时的方向盘最大转矩T hmax，通过Carsim软件进行仿真获得，首先在Carsim中建立目标车型，并设置前轮转向系统类型为手动循环球式，标定往左转方向盘为正，在某一车速下，给方向盘（0～360）°的角输入，取该车速下的最大方向盘力矩T hmax，根据车速感应系数计算的公式，确定了车速感应系数[6]，如表1所示。

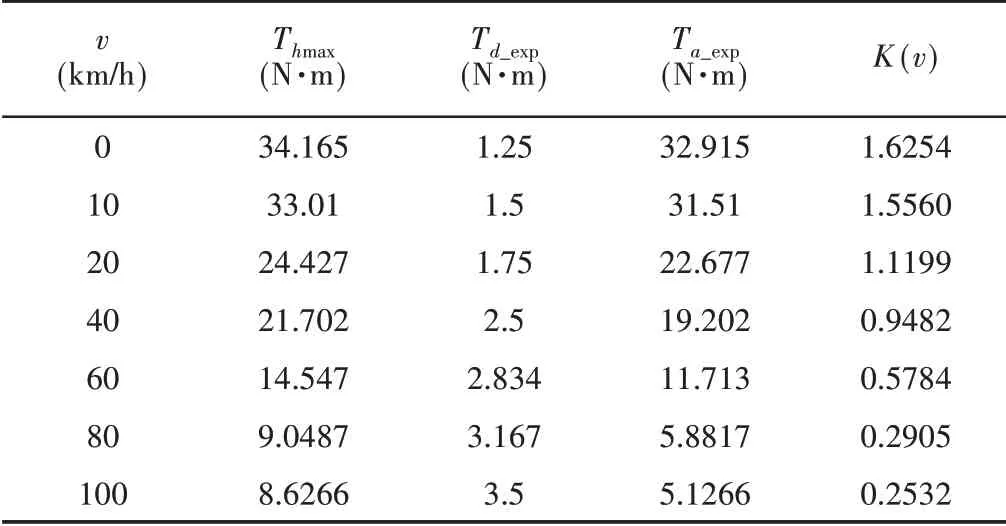
表1 不同车速下的数据值Tab.1 Data Values at Different Speeds

车速感应系数随着车速的增加曾现减小的趋势，在确定了个别车速下的K(v)，利用Matlab多项式拟合工具箱根据获得的散点，完成全车速下车速感应系数的拟合，经过调试，当拟合多项式为3次多项式，如式（4），稳健拟合选用LAR的方式时，得到符合K(v)特征的拟合曲线，如图1所示。

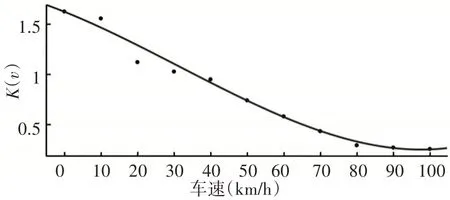
图1 车速感应系数曲线Fig.1 Vehicle Speed Induction Coefficient Curve

2.2 助力特性曲线的设计

汽车在转向助力时，助力电机要随着驾驶员操纵方向盘力矩的大小相互接应，这种对应关系可以用函数f(T d)来表征，操纵力矩增大时，助力电机的输出扭矩要随之增大，要求f(T d)单调递增并保证始终大于零，即f(T d)>0，f'(T d)>0，除此之外，电机输出扭矩还要对操纵力矩的梯度函数单调递增，即f''(T d)>0，因此函数f(T d)可以用式（3）来表征。

式中：a、b、c为待定系数，其中a=0.6。

根据式（1）来确定待定系数的值。

根据表1获得的数据，按照式（7）进行计算，得到助力电机最大助力电流约为Imax≈20A，基于此，建立Simulink模型后，仿真获得目标车型的特性曲线，从图2可以看出，目标电流值随着车速的增加而减小，不同速度之间目标电流值差异并不是等值变化的，是由于K(v)决定的，形状类似开口向上的抛物线。

图2 电动助力特性曲线图Fig.2 Chart of Electric Power Characteristic

3 EPS系统控制策略研究

3.1 助力模式下的传统PID控制策略

PID控制策略通过调节的k p、k i、k d参数值，来控制电机电流输出特性，抵消电机负载，进而实现助力控制，PID控制器的数学描述为[7-8]：

式中：u(k)—PID控制器的输出信号；k p、k i、k d—比例、积分及微分系数；e(t)—测量值与给定值之间的偏差；ė(t)—测量值与给定值偏差的导数。

3.2 助力模式下的BP神经网络控制策略

传统的PID控制策略直接对电机进行闭环控制，依靠调整k p、k i、k d三个参数来得到理想的效果，但是参数的调节存在一定的难度，由于神经网络可以无限接近非线性函数，并且神经网络可以用Matlab的S-Function模块进行搭建，所以可以通过对系统性能的学习来寻找PID控制策略的最优解，采用基于BP神经网络的PID自适应控制，这种控制算法在航天、机械、汽车等其他控制领域得到了广泛的应用，而且控制效果特别好，它是根据增量式PID控制策略的控制原理，对参数k p、k i、k d自学习的神经PID控制，通过反馈型学习和权值调整，使参数能够不断地改变，以使输出的目标电流值能够和目标值达到吻合，也就是参数自整定。BP神经网络的结构，如图3所示。包括输入层、隐藏层和输出层三层。对于电动助力转向系统来说，输入层M个输入节点可以表示为不同时刻的实际电流值、反馈电流值、偏差值和1，Q表示隐层的个数，隐层的神经元个数不宜太多，显然，输出层则为PID控制器的k p、k i、k d三个参数，由于整个控制系统采用的是负反馈，所以k p、k i、k d值要非负，否则会导致系统不稳定，因此将输出层神经元活化函数取非负的Sigmoid函数［9-10］。

图3 BP神经网络结构图Fig.3 Structure of BP Neural Network

由图3可见，BP神经网络的输入层输出为：

网络的隐含层输入为：

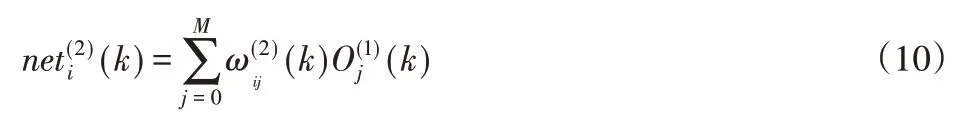
隐层神经元活化函数为：

网络的隐层输出为：

网络的输出层输入为：

式中：—隐层权系数—输出层权系数；带有圆括号的数字1、2和3分别代表输入层、隐含层和输出层。

输出层神经元活化函数为：

网络的输出层输出为：

即可以表示为：

取性能指标函数为：

E(k)根据权重系数的负梯度方向，即根据最陡下降法校正网络的权重系数来搜索调整，并附加惯性项，有：

其中，η—学习速率；α—惯性系数，且

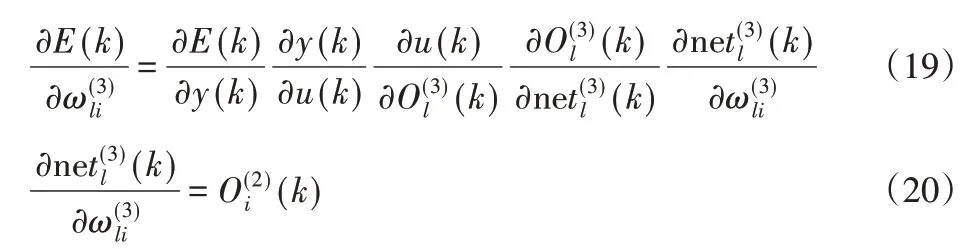
由于∂y(k)∕∂u(k)求不出来，所以用函数sgn[∂y(k)∕∂u(k)]替换，经过替换导致的计算误差，调整学习速率η来补偿。

PID控制器的输出根据经典增量数字PID的控制算法计算，即：

可得：

于是BP神经网络输出层权值系数的公式为：

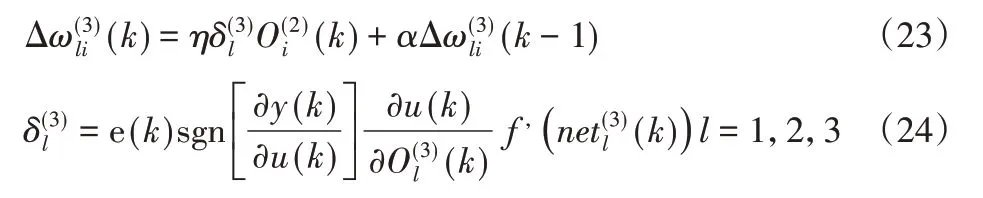
用同样的方法，隐层的权系数学习算法概括如下：

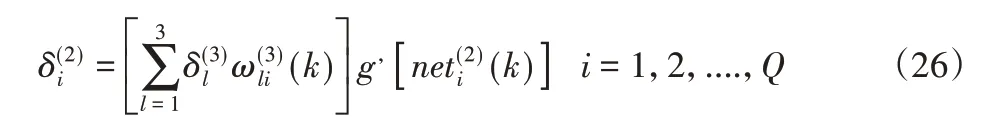
4 电动助力转向系统仿真与分析

4.1 仿真模型的建立与调试

根据BP神经网络的理论基础，BP神经网络模型的功能由Simulink的S-Function模块编写，函数调用通过.m文件。并把转向系统的模型进行结合，同时设置如图3所示的5个隐含层神经元，然后选择学习速率η=0.25和惯性系数α=0.01，得到BP神经网络模型，如图4所示。电动助力转向系统的仿真模型，同样通过Matlab∕Simulink设定，如图5所示。图中目标汽车模型由Carsim软件进行设定，把转向系统的转向类型可调节为手动循环球型，由于方向盘的转矩和电机辅助力矩通过循环球式转向器传递给摇臂轴，进而控制车轮转向，为了使系统闭环，将方向盘转矩和电机辅助扭矩之和作为Carsim的输入，并且把汽车行驶时的车速和转向器转向摇臂转角作为输出，对建立好的联合仿真模型，通过软件仿真的方式，进行相关分析和验证[11-14]。

图4 BP神经网络控制策略图Fig.4 Control Strategy Chart of BP Neural Network

图5 系统仿真模型Fig.5 System Simulation Model

4.2 仿真结果与分析

电动助力转向系统在助力模式下工作时要能够保证转向的轻便性，为了减少驾驶员的转向负担，转向模拟试验用于验证BP神经网络控制策略在助力模式下的控制效果，在车速为10km∕h时，方向盘逐渐施加从中间位置到左侧5N·m的力，持续4s，然后逐渐减小至0N·m，持续一秒，然后同样向右转动方向盘，由于没有回正控制，所以需要继续往左施加力才能回到中间位置，以这样的方式，可以获得有电机辅助和无电机辅助两种情况下方向盘转角和转矩的关系结果，如图6所示。从结果可以分析出，达到相同的方向盘转角，有助力会比无助力需要更小的方向盘转矩，能够实现转向轻便性的要求，由于仿真只验证助力模式下的控制策略，所以，用同样的力向左和向右操纵方向盘时，方向盘角度是不对称的，需要通过回正模式进行调整。

图6 方向盘角度和扭矩图Fig.6 Steering Wheel Angle and Torque Diagram

根据Carsim软件辅助设计的曲线型助力特性曲线，可以实现转向过程中要求省力和追求“路感”的矛盾，对于BP神经网络控制策略的控制效果，还可以通过汽车在不同工况下，驾驶员转向时电机输出的实际电流值进行评价，当设定为不同的速度时，给出方向盘(-10～10)N·m的转矩输入，并获得不同工况下的实际电流曲线，如图7所示。通过图7可以看出，采用的BP神经网络实际控制效果通过和图2对比，能够非常接近目标值，因此具有较好的鲁棒性。

图7 不同工况下的实际电流曲线Fig.7 Actual Current Curve Under Different Conditions

由于基于BP神经网络的PID自适应控制策略实现了参数的自动调整，所以提高了工程领域调参的繁琐，对于控制的效果，需要通过试验来验证，EPS系统的控制目标就是实现对目标电流的跟随，因此，在车速分别为30km∕h和60km∕h时，给转向盘6N·m的阶跃输入，仿真步长设定为0.001s，得到两种控制策略的实际电流值与目标电流值的差异情况，如图8所示。

图8 两种控制策略控制效果图Fig.8 Control Effect Charts of Two Control Strategies

从图8的结果可以看出，汽车在低速和高速时，经验法调试的传统PID控制策略控制的实际电流值低于目标值，有可能造成转向不足的问题，而基于BP神经网络的PID自整定控制策略在车速30km∕h时，经过0.125s趋于稳定，虽然略小于传统PID，但是能够和所期望的理想目标值达到较高的吻合，在车速60km∕h时，比传统PID有着较小的波动，经过一个超调后就趋于稳定，整体性能优于传统PID控制策略。

5 结论

（1）以循环球式转向器作为转向机构的轻型货车作为研究对象，对助力模式下的控制策略进行了探究，利用Carsim软件具有接近实车模型的优势，确定了车速感应系数，设计出了兼顾轻便和“路感”的曲线型助力特性曲线。（2）通过BP神经网络自学习和权值调整的优势结合PID控制算法，实现了PID算法参数的自整定，然后通过仿真试验验证了BP神经网络控制策略不仅能到实现助力模式下转向轻便的效果，而且对目标电流具有较好的跟随性，比传统的PID控制策略具有较高的鲁棒性。