一种基于指数趋近律的非线性系统变结构轨迹跟踪控制新方法

田 霖, 孙 亮, 刘冀伟

(1.北京科技大学 自动化学院，北京 100083； 2.民政部一零一研究所，北京 100070)

在许多控制系统设计过程中，常常面临实际对象和所建立的面向控制的数学模型之间存在差异的问题，这些差异主要源于系统中存在的参数不确定性、外部未知干扰、未建模动态及参数等。因此设计能克服这些差异的鲁棒控制算法成为一个挑战。强大的鲁棒性滑模变结构控制成为一种能有效克服这些模型差异的控制算法[1-3]。

多年来，滑模变结构控制的研究成果不断涌现。为了减少到达滑模面的时间，文献[2]和文献[3]通过等价控制输入提出了指数趋近律方法并得到了大量推广和应用。进一步，文献[4]采用指数函数设计了一种非线性趋近律，动态调整受控系统的变化过程，并将其应用到多输入多输出非线性系统。文献[5]基于指数趋近律设计了一种分层滑模变结构控制器。在许多实际应用中需要采用观测器估计系统的不可测干扰以保证系统状态在模型存在不确定性的情况下也能收敛。文献[6]针对一类含有不匹配干扰的非线性系统设计了一种非线性干扰观测器。文献[7]针对一类非线性拉格朗日系统的定点调节和轨迹跟踪问题，借助低通滤波器估计未知干扰并设计出一种不连续的鲁棒干扰观测器。文献[8]采用一种不确定性和干扰估计器技术设计了一种新的能抑制控制输入抖振的边界层滑模变结构控制器。文献[9]针对滑模变结构控制中出现的抖振问题，提出一种基于分段函数的幂次趋近律方法，加快了系统跟踪误差的收敛速度。文献[10]以一类非线性模型作为研究对象分析了滑模变结构控制趋近运动边界特性，给出状态变量范数的约束关系式。目前，滑模变结构控制方法已经推广到大量实际系统中，包括单相全桥逆变器[11]、永磁同步电机[12-13]、开关电源[13]、火箭发射系统[14]、汽车转向系统[15-16]、机器人系统[17]等。近年来，对经典滑模控制的改进和扩展仍在继续，但很多结果由于控制器结构复杂或计算量大等因素难以确保优良动静态性能。

笔者针对不确定二阶非线性机械系统轨迹跟踪过程中，当模型参数具有不确定性和未知外部干扰时，基于新的指数趋近律提出一种非线性机械系统的滑模变结构轨迹跟踪控制器。所设计的指数趋近律可以确保滑模控制器动态适应跟踪误差的变化过程以减少状态到达滑模面的时间，进而提高系统状态的收敛速度。基于李雅普诺夫稳定性理论证明所设计的变结构控制器可以保证系统轨迹跟踪误差的渐近收敛性。以质量-弹簧-阻尼器系统和两自由度刚性机械臂作为仿真算例，验证了所提出控制器的有效性。

1 问题描述

考虑一类由Eluer-Lagrange方程描述的二阶非线性全驱动机械系统动力学模型[17]：

(1)

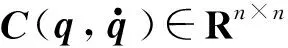
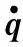
2 基于指数趋近律的变结构控制器设计

2.1 基于计算力矩法的控制器设计

当不精确知道系统惯性参数且干扰未知时，可取控制律为

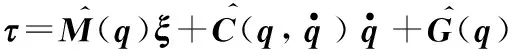
(2)

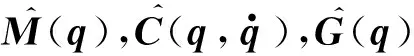
(3)

即

(4)

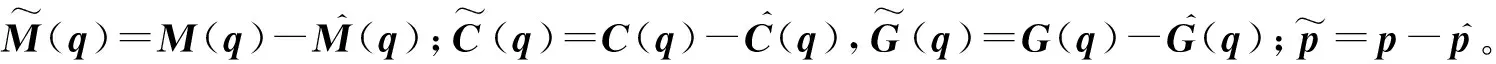
(5)

(6)

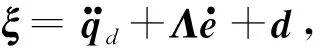
(7)

(8)

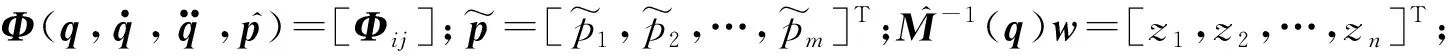
(9)

因此，基于新的指数趋近律设计滑模变结构控制器为

(10)

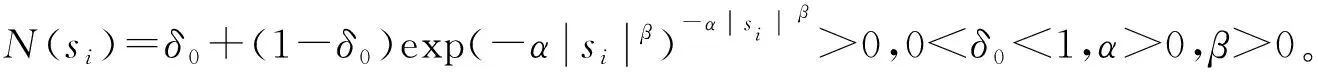
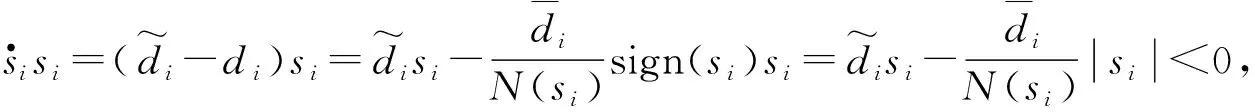
(11)

其中：

再代入式(2)最终可得到基于计算力矩法的指数趋近变结构控制律为

(12)

注意到采用式(12)所示的控制律可以得到系统的指数趋近律为

(13)

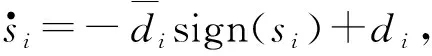
2.2 基于输入输出稳定性理论的控制器设计

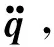
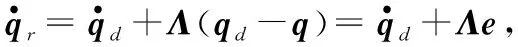
(14)

则取控制律为

(15)

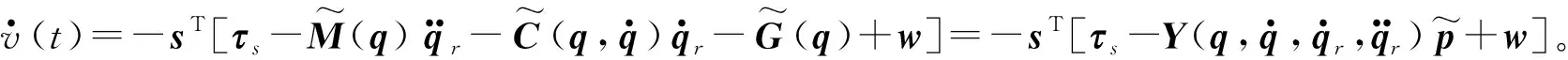
(16)

(17)

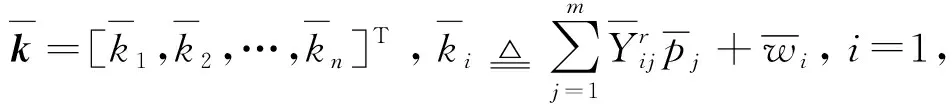
下面对所提出的闭环控制系统给出稳定性结论。

定理针对式(1)所示的系统，参数不确定性有界及外部干扰有界的假设条件下，若两类不同的滑模变结构轨迹跟踪控制律(式(12)和式(15))的参数都满足0<δ0<1，α>0，β>0，κ>0时，则可以保证闭环系统是渐近稳定的且基于计算力矩法的变结构控制器的滑模面到达时间相对经典滑模面更短。

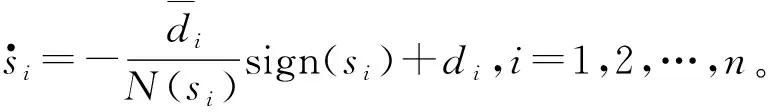
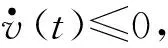
接下来证明所设计的变结构控制律(式(15))也可以保证闭环系统渐近稳定。若采用该控制律则闭环系统方程为

(18)

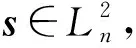
2.3 抖振的消除

变结构控制的一个明显缺点是切换时由于惯性和时滞的影响，使得滑动运动叠加上一个高频抖动，称为抖振。常用的消除抖振方法是在滑模面两侧增加一个边界层，并在边界层中用饱和函数替代符号函数，即将变结构控制律中符号函数sign(si)替换为饱和函数[19]：

式中：ε>0为边界层厚度。需要注意的是，此时变结构控制只能保证所有轨迹都进入边界层，而不能保证都进入滑模面，故若边界层厚度过大，会产生较大的稳态误差。

3 仿真算例

如图1所示，笔者分别针对单输入单输出的质量-弹簧-阻尼器机械系统[8]和多输入多输出的平面刚性机械臂关节运动系统[17]两个典型算例，应用MATLAB仿真软件对所提出的式(15)所示的控制算法进行验证。类似地，对式(12)所示的控制算法也可进行仿真验证，在此不再赘述。

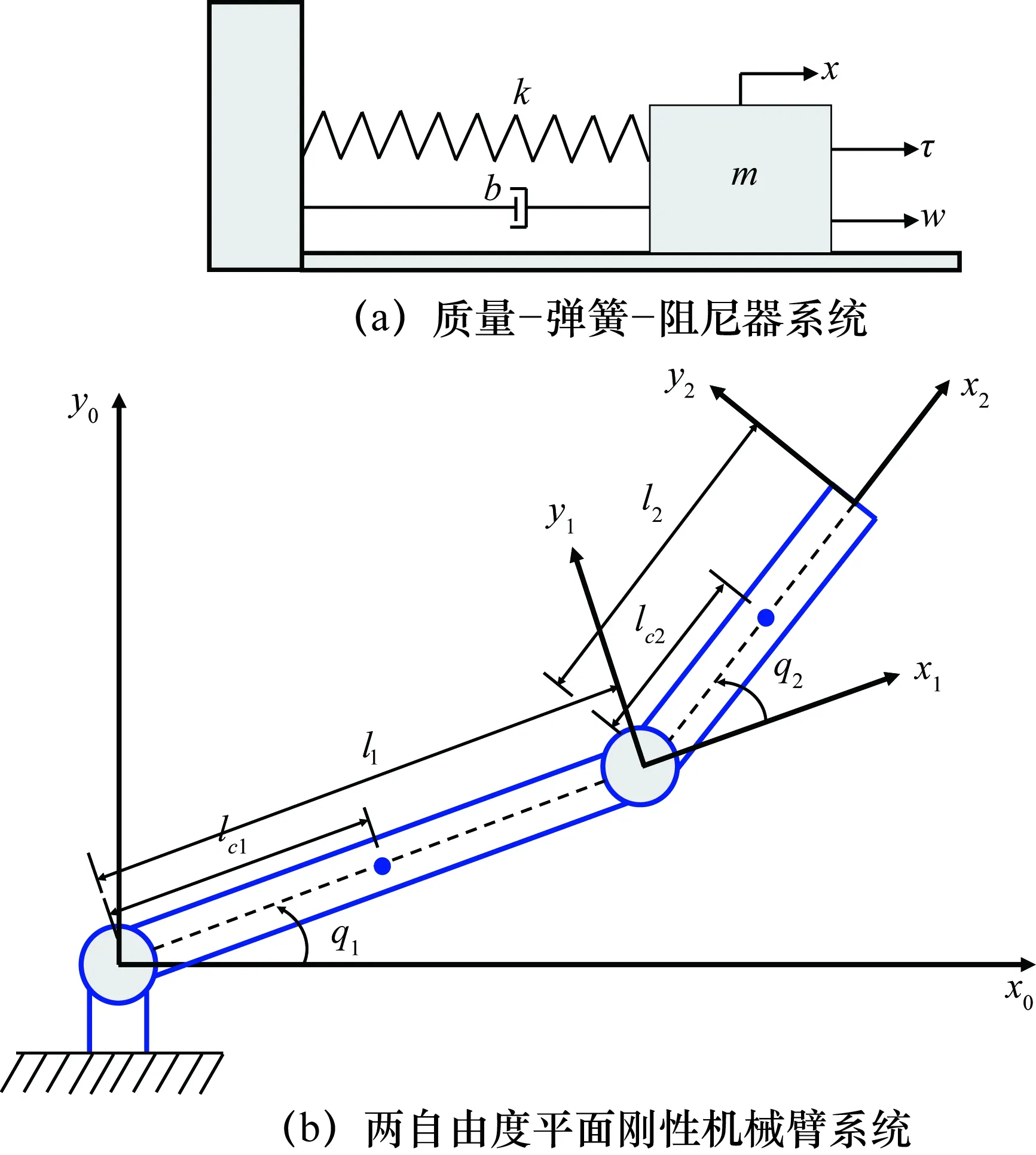
图1 两类典型机械系统

其次，建立两自由度平面刚性机械臂关节动力学模型(如式(1)所描述)，其中机械臂关节角位置向量为

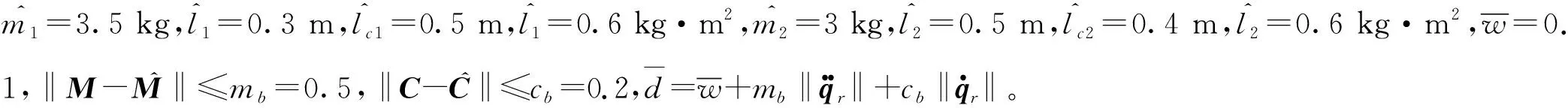
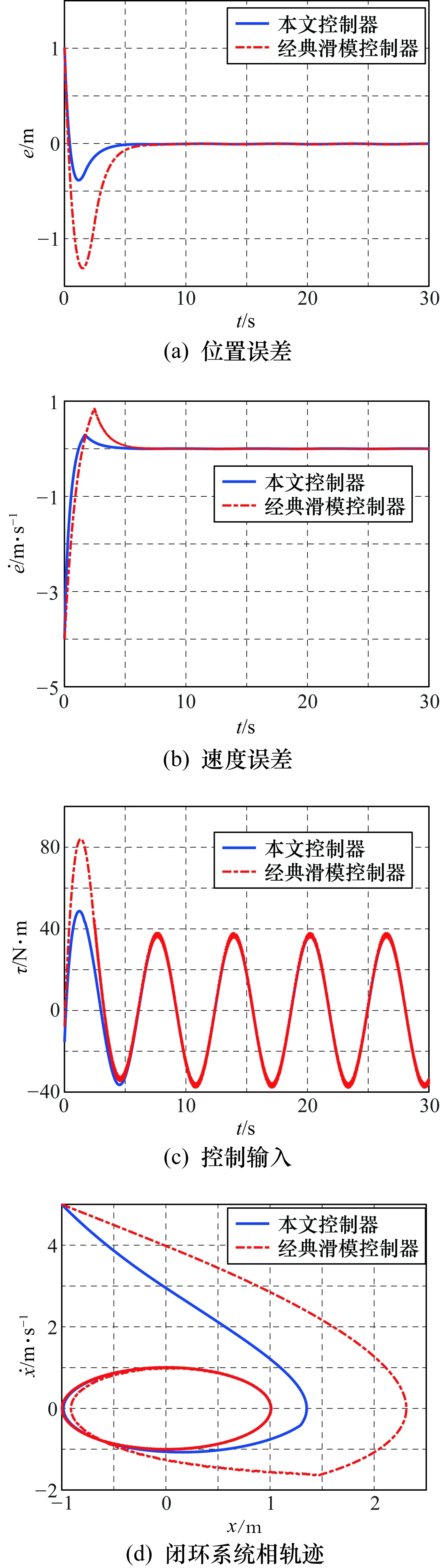
图2 质量-弹簧-阻尼器系统轨迹跟踪效果

图3 两自由度平面刚性机械臂关节轨迹跟踪效果

4 结束语

针对不确定二阶非线性机械系统提出了基于一种新的指数趋近律的滑模变结构控制方法。所提出的变结构控制器通过采用一种良好特性的非线性函数对经典滑模控制的滑模面趋近阶段收敛性能进行改进，减小了系统过渡过程时间，提升了系统的动态品质。并且设计了变结构控制器对系统参数不确定性和未知外部干扰进行抑制，并采用边界层法有效消除抖振对系统控制性能的影响。设计的滑模变结构控制方法可实现多输入多输出不确定非线性机械系统的高精度轨迹跟踪控制。最后在仿真算例中通过对控制器进行参数整定，使闭环系统满足动静态性能要求。理论分析和仿真结果证明了所设计的变结构控制方法的有效性。未来将开展在质量-弹簧-阻尼器系统和两关节机械臂系统等实验平台中的控制算法仿真验证。