基于CEEMDAN的MEMS加速度计输出信号降噪方法

周 涛

(平煤股份煤炭开采利用研究院，河南 平顶山 467099)

输电线路杆塔对导线、避雷线起重要支撑作用，它的结构稳定性是整个电力网络系统运行安全的重要保障[1]。但是由于受采空区特殊地质条件的影响，使得采空区的高压输电杆塔会因为天气、地质及本体因素而发生摆动倾斜，容易引起停电并导致出现安全事故。输电线路杆塔倾斜监测技术研究使采空区高压输电系统位移监测变被动防御为主动预防，通常采用加速度计采集杆塔的倾角监测数据，但是由于严酷的现场环境，加速计会存在精度误差,主要有随机游走误差和对准误差。其中，对准误差可以通过标定和对准进行消除[2]；随机误差通常包括零偏不稳定误差和角度随机游走误差，角度随机游走误差是由速率白噪声积分引起的具有游走特性的误差增量，可用白噪声表征，而零偏不稳定误差为加速度计内部产生的低频分量(1/f噪声)，因此加速度计输出的信号夹杂白噪声和1/f噪声，直接影响杆塔倾斜角计算的精确度。所以对采集的加速度计信号进行降噪处理是准确获取杆塔运动参数至关重要的一步。

1/f噪声为非平稳性、自相似性的信号，经研究发现，其在多尺度分解下呈现自相似性和相关性，因此多用多尺度分析算法处理。在工程实践中，很多学者对加速度计输出信号处理精度问题进行了研究。文献[3]采用卡尔曼滤波法对数据进行降噪处理，但存在滤波发散的问题；文献[4]采用小波分析方法，但其降噪效果直接受基函数与分解尺度的选择影响；文献[5]采用BP神经网络，但提高精度需训练大量的数据，存在计算量大的弊端；文献[6]采用FIR滤波,但数字滤波器不能有效消除与有效信号频带相近的噪声影响，适应性较差；文献[7]采用经验模态分解(Empirical Mode Decomposition,EMD)表现出有效性，但存在过分解、模态混叠、端点效应的问题。

自适应噪声完备集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,CEEMDAN)方法弥补了EMD过程中的缺点，同时提高了计算效率，增加了重构精度，更适合非线性信号的分析[8]。文献[9]采用CEEMDAN和排列熵(Permutation Entropy，PE)对冲击振动信号降噪，克服了模态混叠问题，达到了滤除信号中高频噪声和基线漂移的效果，但是有效信号中依旧存在伪分量和低频噪声分量，针对这个问题，采用在滤除信号随机噪声方面有显著效果的奇异值分解算法进行二次滤波来提高信号的信噪比，并运用K-means聚类算法确定奇异值有效阶次，将特征分量和二次滤波后的特征分量进行重构，最终得到有效且完整的倾斜加速度信号。

1 算法原理及步骤

1.1 CEEMDAN算法原理

CEEMDAN为EMD、EEMD的改进算法。EMD将原始信号划分为从高到低的几个频率阶的模态分量，但是EMD方法存在模态混叠、末端效应等弊端[10]。常用的EEMD和CEEMD方法运用添加均值为0的高斯白噪声辅助分析，虽在一定程度改善了EMD算法存在的模态混叠问题，但未完全消除，同时为了消除添加白噪声的影响，提高重构信号精度，需要多次集成平均，迭代次数增加导致计算效率下降，而CEEMDAN计算效率高、重构误差低[11]。CEEMDAN算法具体实现步骤如下。

① 将满足N(0，1)分布的白噪声wi(t)添加到原始信号y(t)中，则第i次的信号可表示为

yi(t) =y(t) +wi(t)

(1)

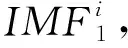
(2)

残余分量为

r1(t) =y(t) -IMF1

(3)

② 将白噪声添加到残余分量r1(t)可得

(4)

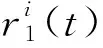
(5)

③ 重复以上过程步骤m次，直到残差余量不适合被分解便结束运算，则信号y(t)可表示为

(6)

1.2 奇异值分解原理

奇异值分解(Singular Value Decomposition,SVD)利用正交矩阵分解技术将含噪信号矢量空间分解为“信号子空间”和“干扰子空间”,是一种有效的非线性信号处理方法，在信号去噪方面效果显著。SVD降噪的步骤如下。

① 首先将原始带噪一维信号Y=[y(1),y(2),…,y(n),…,y(N)]构造成p×q阶Hankel矩阵H。

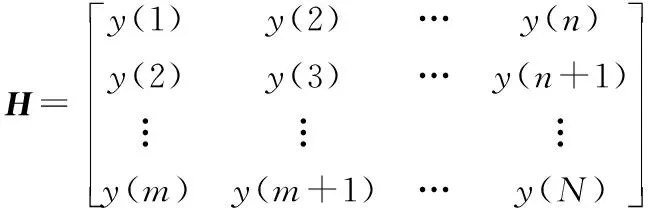
(7)

② 对构造的Hankel矩阵进行SVD,一个m×n的矩阵H会存在m×m的正交矩阵U和n×n的正交矩阵V，使得

H=USVT

(8)

式中:S为m×n的非负对角阵，即

S=diag(σ1,σ2,…,σr)

(9)

式中：σ1,σ2,…,σr为矩阵H的奇异值，并按从大到小的顺序排列。

③ 有效阶次的确定。SVD降噪效果取决于如何选取有效信号对应的奇异值序列，一旦有效阶次选择过高，经SVD降噪的分量中依旧存在高频噪声信号，反之则易出现有效信号保留不完整。由于前几个数值较大且排列离散的奇异值贡献了重构有效信号，后面的数值较小且排列紧密的奇异值贡献了重构噪声信号，因此采用奇异值序列子集的离散程度来确定SVD的有效阶次，将奇异值子集的标准差和奇异值作为奇异值序列的特征量。通过K-means聚类算法将奇异值分为两类，一类对应加速度信号，另一类对应噪声信号。保留信号子空间，抑制噪声子空间声[12]，即得到降噪信号。

SVD得到的奇异值数值作为奇异值序列的特征量F1=σ1,σ2,…,σr，定义奇异值序列子集群为

(10)

计算各个奇异值序列子集标准差stdn，作为奇异值序列的另一个特征量F2=SD(std1)，SD(std2)，…，SD(stdn)，通过K-means聚类算法对基于F1和F2特征量的奇异值序列进行二分类，计算有效特征信号对应的奇异值子集的个数，即可得出重构奇异值的有效阶次。

④ 利用奇异值逆分解得到重构后的矩阵A，矩阵A的反对角线求平均即可得到真实信号y(i)，i=1,2,…，N。

1.3 CEEMDAN-SVD联合降噪算法

CEEMDAN对非平稳非线性随机信号有很强的适应性，但为了防止CEEMDAN算法在抑制高频噪声分量的同时丢失相应分量中的特征信号所导致的重构信号误差大的问题，本文利用PE作为确定需要进一步降噪处理信号分量的阈值，并选择SVD作为二次滤波方法，从而有效地保留了有效本征模态函数(Intrinsic Mode Function,IMF)分量。

CEEMDAN-SVD联合降噪算法具体步骤如下。

① 首先将原始加速度信号利用CEEMDAN分解为从高到低排列的几个频率阶的模态分量。

② 用PE作为筛选出高噪频率分量及确定需要进一步滤波的IMF分量的阈值，计算各个模态分量的PE值，当PE>0.707时为高频噪声分量，考虑低频噪声的影响，PE>0.6 时则认定为含噪 IMF分量[13]，PE在0.15左右时为正弦信号分量直接保留。

③ 筛选出的信号成分和噪声成分混叠的IMF分量利用SVD进行二次滤波。

④ 最后将SVD降噪后的IMF分量和有效特征信号的IMF分量、残余分量进行重构，可得到降噪后的MEMS(Micro Electro Mechanical System，微机电系统)加速度计输出信号。CEEMDAN-SVD降噪流程图如图1所示。

图1 CEEMDAN-SVD降噪流程图

2 仿真实验

杆塔倾斜加速度计信号仿真信号的表达式为

Z(t)=βsin(2πft)

(11)

1/f噪声由分式布朗运动(Fractional Brownian motion，FBM)模型仿真[14]可得

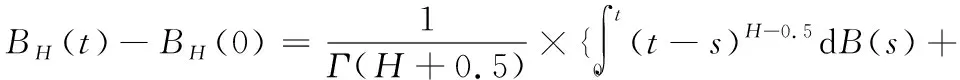
(12)

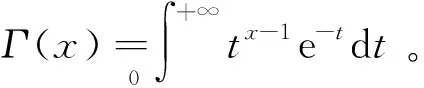
仿真含噪加速度计信号为

y(t)=w(t)+s(t)

(13)

X(t)=A1sin(20t+φ)+A2sin(40t+φ)+y(t)

(14)

式中：A1=10 mm,A2=3 mm·s-2，φ=30°;y(t)为噪声信号;w(t)为-1 dB白噪声；s(t)为1/f噪声，其中H=0.3，采样点数N为2000；采样频率fc为1000 Hz。振动加速度信号如图2所示，加入噪声后的加速度信号如图3所示。

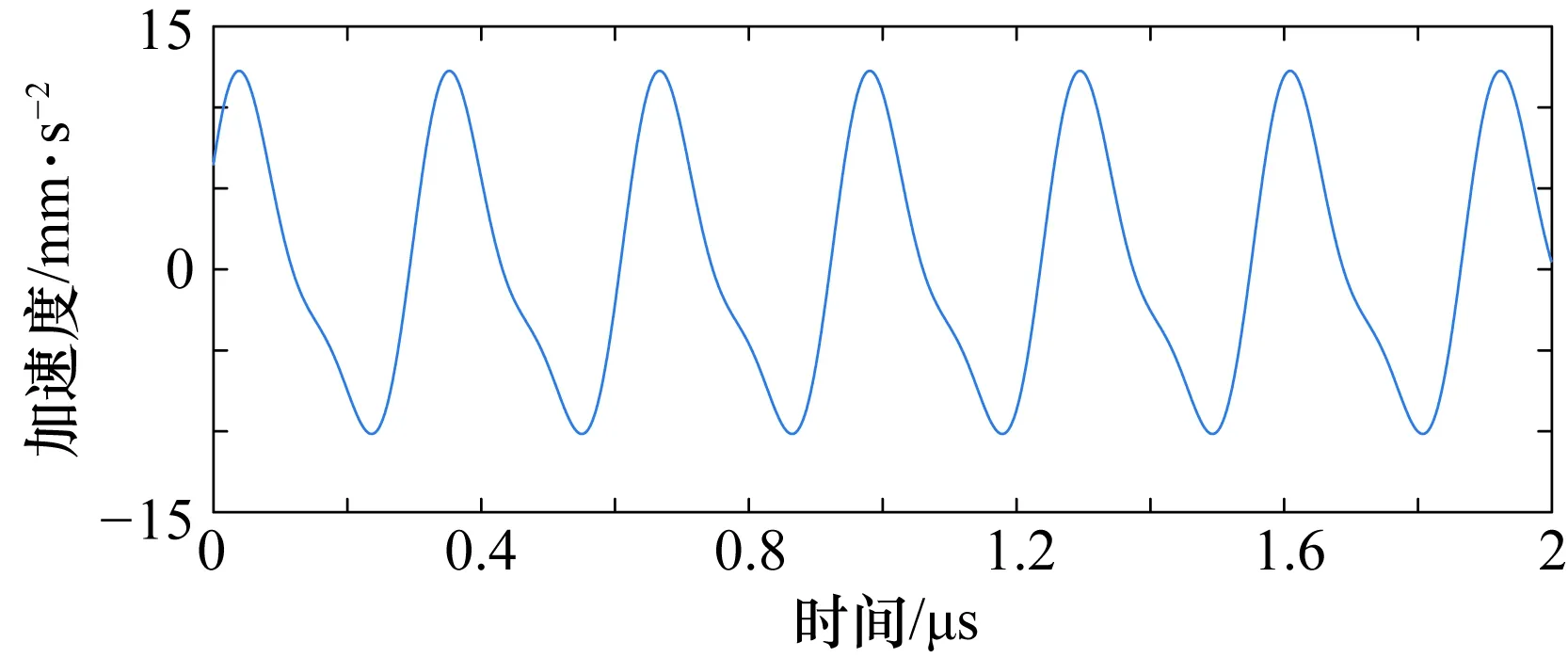
图2 加速度信号

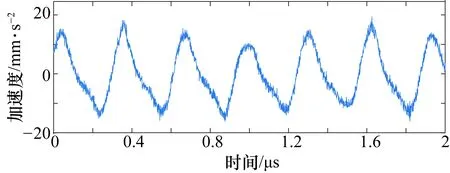
图3 加噪后的加速度信号

对原信号进行CEEMDAN得到的9个IMF分量如图4所示。

图4 含噪加速度信号经CEEMDAN得到的各IMF分量

从图4可以看出，随着分解层数的增加，IMF分量的频率越来越低，信号的变化趋势被突显出来。计算PE值时，选择嵌入维度m=6 和时间延迟T=1，对各IMF分量进行PE值计算，各PE值如表1所示。

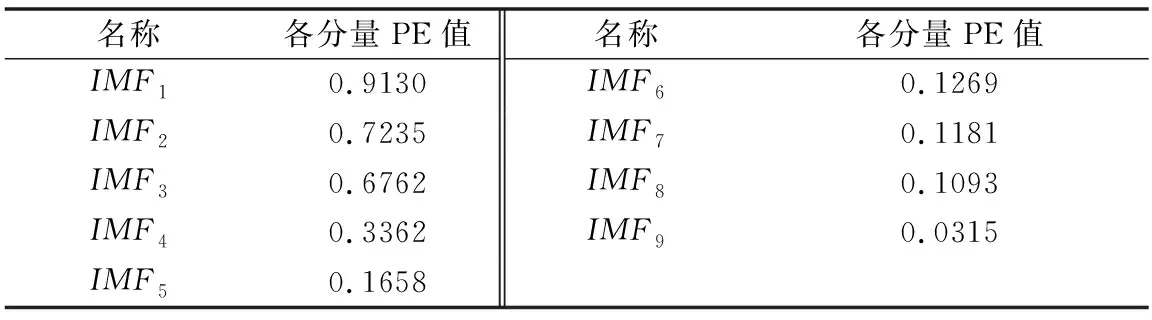
表1 各IMF分量的PE值

PE(IMF1)、PE(IMF2)均大于0.707，因此IMF1、IMF2为高频噪声分量舍弃。PE(IMF3)、PE(IMF4)均在0.6～0.707范围内，因此IMF3、IMF4为含噪特征信号，剩余分量为特征信号和残余分量。

将IMF3、IMF4分量构建1000×1000的Hankel矩阵，然后进行SVD得到奇异值矩阵，绘制奇异值序列图5所示，奇异值K-means聚类效果图如图6所示。由图6可以看出IMF3重构奇异值有效阶次为4，IMF4重构奇异值有效阶次为7。

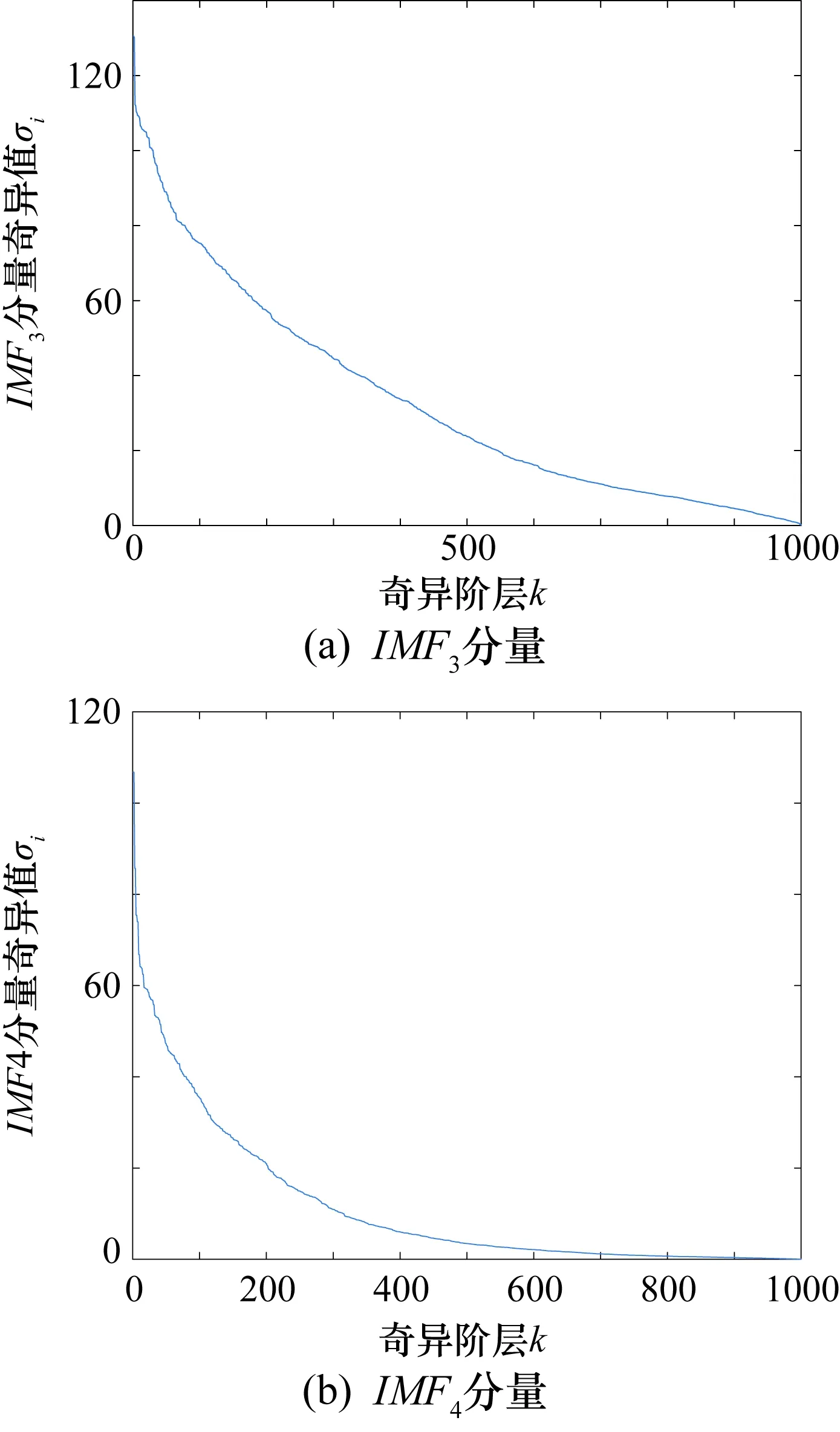
图5 奇异值序列图

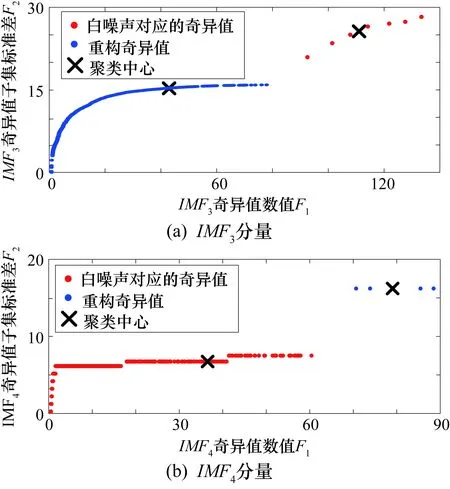
图6 奇异值K-means聚类效果图

保留有效奇异值阶次后，通过SVD重构得到降噪后的IMF3分量和IMF4分量与IMF5～IMF8特征分量及IMF9残余分量重构得到的降噪加速度计输出信号，通过本文方法处理后如图7所示。

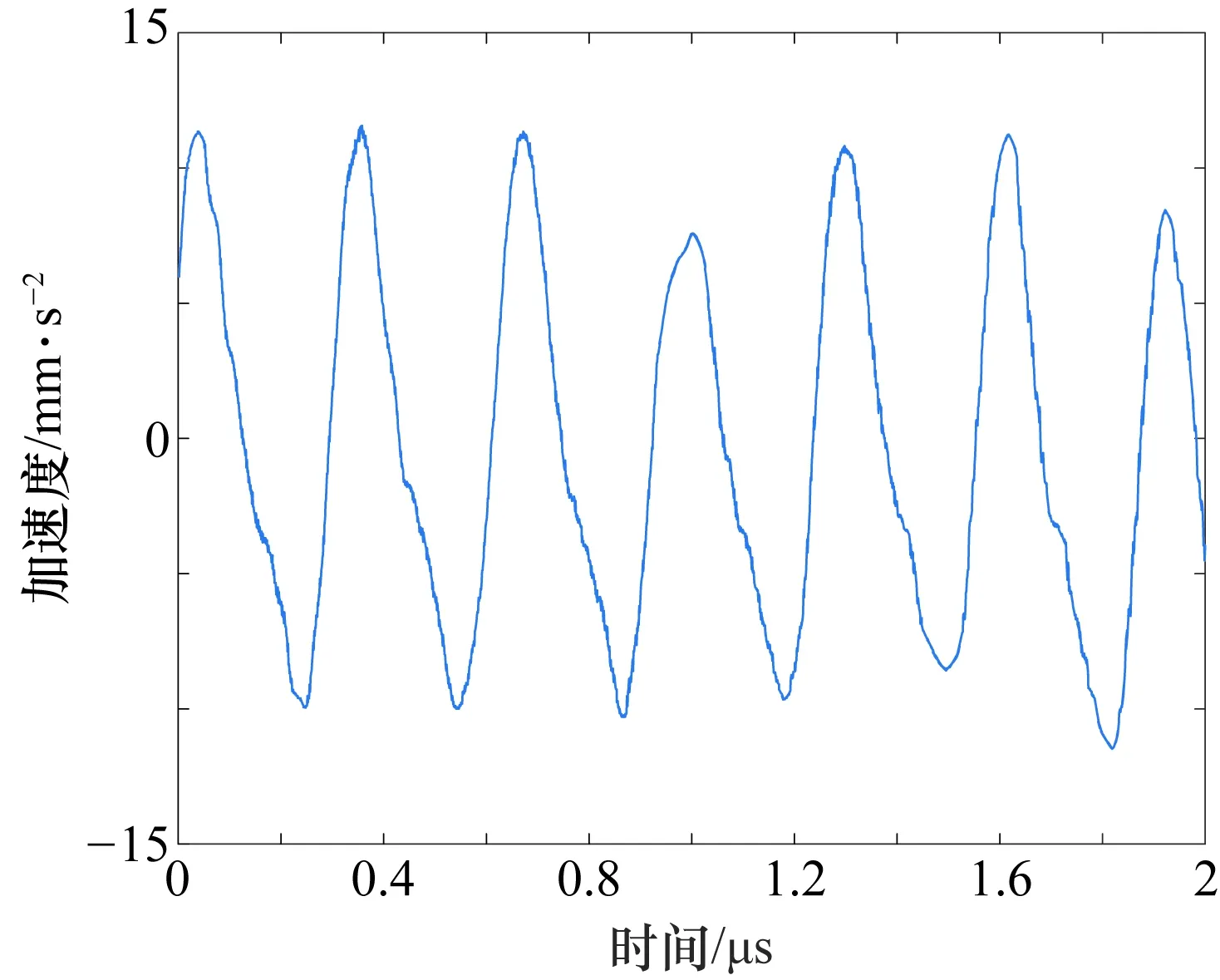
图7 CEEMDAN-SVD降噪处理后的加速度计输出信号

为了验证方法在不同噪声环境下的加速度信号的降噪效果，加入3 dB、1 dB高斯白噪声，经过处理，引入信噪比(Signal to Noise Ratio，SNR)、均方误差(Mean Square Error,MSE)来评价经本文算法处理信号的降噪效果，降噪效果如表2所示。

(15)

(16)

表2 不同信号噪声强度下的去噪效果

为了对比降噪效果，利用扩展卡尔曼算法[15]和CEEMDAN-PE两种方法对仿真信号进行处理，滤波结果如图8、图9所示。经过不同方法处理后的去噪效果如表3所示。

图8 扩展卡尔曼滤波处理后的加速度信号

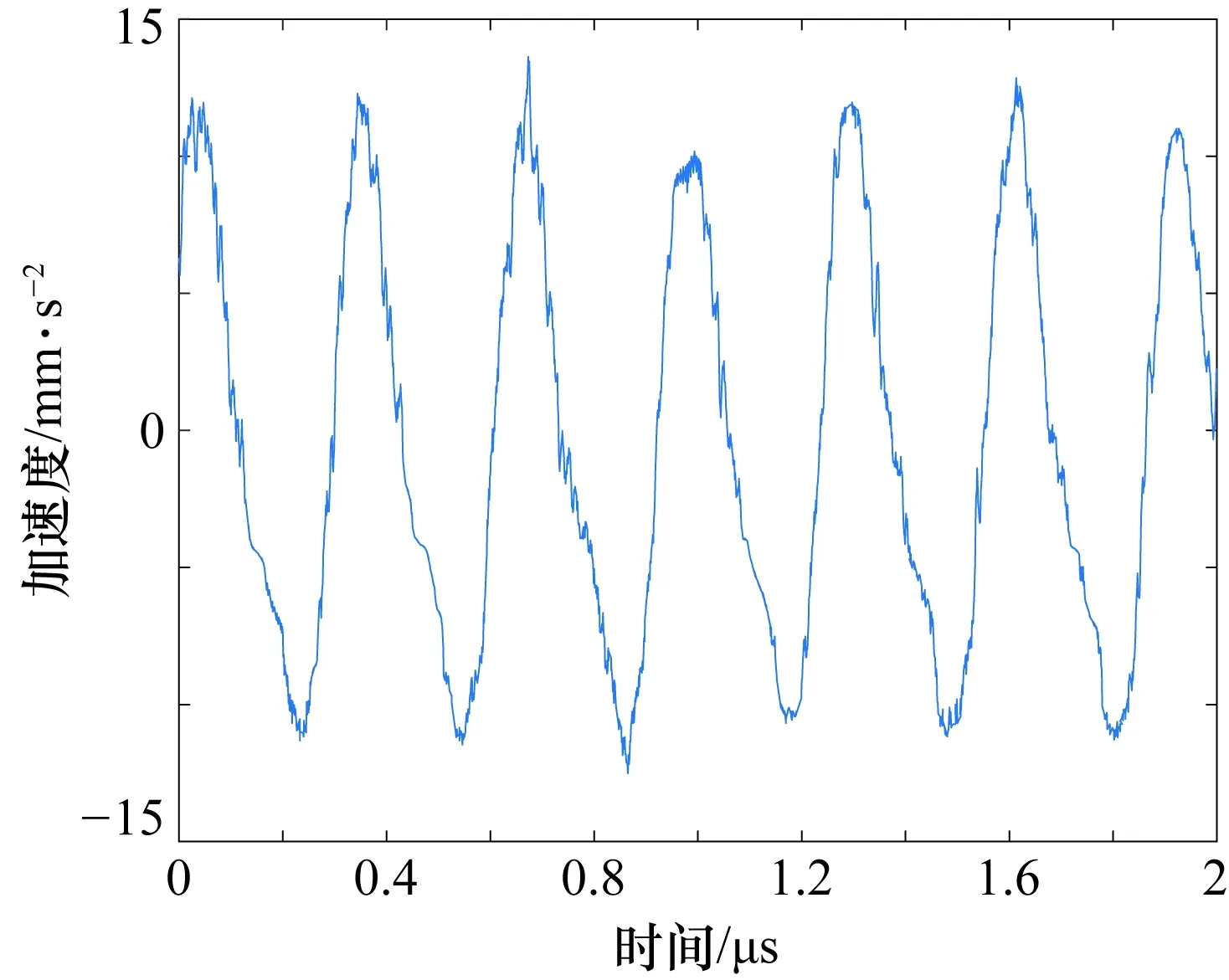
图9 CEEMDAN-PE滤波处理后的加速度信号

表3 不同方法下同一信号的去噪效果

由图7～图9降噪效果对比可知，笔者提出的CEEMDAN和SVD联合降噪效果最好，不仅能滤除高频噪声，而且能滤除低频闪烁噪声，较高程度保留了信号的有效特征。

3 实验

为验证所提出的降噪算法对杆塔倾斜信号的测量准确性的影响，实验数据利用MEMS陀螺仪和MEMS加速度计、MPU6050磁传感器等集成的MIMU(Miniature Inertial Measurement Unit)完成采集。当模拟杆塔发生倾斜，由MIMU的加速度传感器采集到的数据作为原始数据，并即时计算角度值，对其进行CEEMDAN-SVD滤波降噪处理后，获得杆塔有效的三轴姿态角，并利用高速摄像机成像测量的方法测量杆塔倾斜情况并做对比，选取200个数据进行分析，MIMU采集并经滤波后数据与高速摄像机采集的数据对比如图10所示。

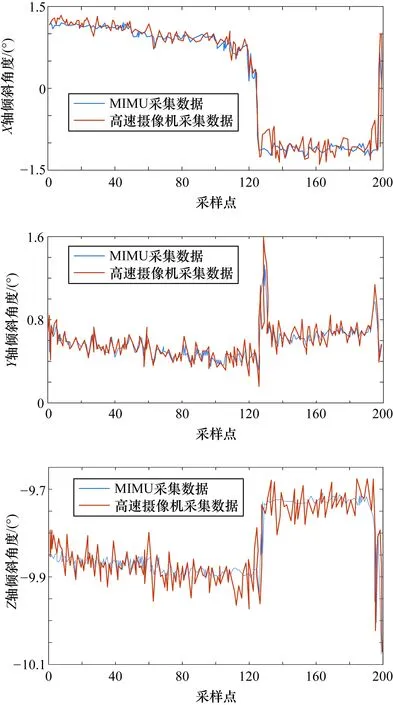
图10 MIMU采集并经滤波后的数据与高速摄像机采集的数据对比图

由图10可以看出，在前120个采样点中，模拟杆塔处于不受力的状态，三轴倾斜角没有明显变化；120个采样点左右3个轴的倾斜角度发生瞬时变化，变化幅度大于1°，说明模拟杆塔受到应力发生了倾斜。两组数据近似偏差在0.2°以内，可以看出经过本文算法处理后的三轴加速度数据经运算得出的倾斜角度与高速摄像机采集实际数据运算得出的倾斜角度偏差很小，即证明该算法起到了良好的降噪效果，提取滤波处理后的加速度计输出信号保留完整且特征明显，提高了倾斜角度测量精度。

4 结论

① CEEMDAN可以将原始加速度信号分解成从高到低排列的几个频率阶的模态分量，有效解决了EMD中存在的模态混叠问题，且较大程度地保留了加速度计输出信号的波形特征。

② 通过K-means聚类算法来确定SVD的有效阶次，来滤除含噪特征分量中的噪声，实现信号的二次滤波。

③ 通过仿真和实验分析，对比不同信号噪声强度下和相同信号下扩展卡尔曼滤波、CEEMDAN-PE降噪效果，结果表明本文方法能更准确地保留信号的特征形态，信噪比和均方根误差均有所改善。

④ 证明通过对加速度计输出信号的滤波处理，可降低误差，并提高了杆塔倾斜监测系统运动参数精度。