认知雷达参数化波形设计
乔 凯 蔡兴雨 董 国 王 旭
(西安电子工程研究所 西安 710100)
0 引言
传统体制雷达通常以相对固定的工作模式来发射固定的波束、电磁波形式,同时以相对固定的模式来接收处理回波信号[1]。然而,随着雷达作战环境越来越复杂,雷达所需探测的地面和空中目标愈加多样,同时随着电子战技术的飞速发展,雷达所面临的电磁环境也更加复杂,传统雷达很难满足现代战争对雷达系统的需求[2]。而认知雷达可利用目标和环境的先验信息,通过算法优化设计发射波形,合理分配雷达发射资源,同时可自适应优化接收处理,实现雷达接收到发射的闭环,能够很好地提升雷达的探测性能和阵地适应能力。
目前,对于认知雷达的研究主要体现在对认知雷达架构及参数化模型的建立、对认知雷达资源管理调度、对认知雷达关于对环境及目标先验信息的处理算法这几个方面[3]。本文则从认知雷达架构入手,对认知雷达架构进行进一步优化,阐述认知雷达参数化理念和参数化的必要性;从雷达方程入手,结合认知雷达一般调度需求,确定参数化波形的结构及具体参数,建立起一个完整的参数化波形,并进行仿真验证。通过对认知雷达的参数化波形进行建模研究,可有效解决认知雷达在工作时资源调度不全、参数化波形不能很好地表征雷达整体控制的问题;可为雷达资源管理提供支撑,解决雷达资源调度时应该怎样调度雷达参数的问题;也可为雷达波形库的建立提供支撑。
1 认知雷达参数化概述
1.1 认知雷达概述
与传统雷达相比,认知雷达不仅仅是简单的发射与接收,而是实现了“发射机-综合电磁环境-接收机-发射机”的自适应闭环处理流程[4]。其不仅接收回波信息来获取目标信息,还可获取干扰、噪声、杂波等综合环境信息,自适应处理可通过环境信息和回波信息并结合先验信息来进行运算,决定下一次的发射最优波形和雷达控制参数,形成“发射波形-接收回波-发射波形”的闭环[5]。
1.2 认知雷达架构
认知雷达架构最早由Haykin S教授在2006年提出;之后Haykin在2012年对认知雷达架构进行改进,加入模型库与波形库的概念[6];文献[7]给出了认知雷达的详细体系架构;综合文章中的论述,对认知雷达智能调度系统进行详细设计改进,认知雷达的架构及工作模式如图1所示。

图1 认知雷达结构及工作模式
图1中对认知雷达架构进行了详细的表述,并对认知雷达工作中的信息流进行了简要表示。雷达根据任务类型初步选择一系列参数化波形并通过高性能射频前端发射;接收后根据回波信息进行自适应处理,智能调度系统通过处理后的信息获取到雷达的周围环境信息和目标信息,自适应选择其下一组发射参数和处理参数,并将下一组控制信息发送于信息处理机与前端,进行下一轮发射。雷达操控者也可通过人机交互系统自行选择雷达的控制参数。
1.3 认知雷达参数化波形概念
参数化即用参数来表征模型[8]。对于雷达来说,雷达参数化即用参数来表征雷达各部分模型,参数化波形即用一系列参数表示雷达所需要控制的各种资源,是对雷达一系列控制参数的描述。雷达通过计算,选择最优的参数化波形,再通过对参数化波形的实时调度,即可实现不同功能。
参数化波形在雷达资源调度系统中使用,而雷达可调度的资源可分为软件资源和硬件资源,参数化波形则需要做到在硬件条件满足的情况下,对雷达所有的参数资源都能描述到,这样才可最大限度地满足雷达的灵活性要求。从雷达模块的角度来说,对雷达资源的描述也可以从前端参数、处理参数、检测参数这三个方面来描述。从雷达参数类型角度来说,雷达控制参数可从时域参数、频域参数和空域参数这三个类型来进行描述。

图2 雷达参数化资源分类
认知雷达中对雷达进行参数控制是十分重要且必要的一环,通过从时域、频域、空域这三个方面对雷达资源进行描述、对雷达进行控制,可有效实现认知雷达闭环结构中通过判断回波对雷达的再控制过程,本文之后将从这三个方面对雷达参数产生进行具体分析。
2 雷达参数化波形建模
2.1 雷达基本参数
雷达方程的一种基本形式为
(1)
式(1)表明了雷达最大作用距离与雷达各个参数以及目标特性之间的关系。其中,Rmax为雷达的最大作用距离,Pt为雷达发射功率,G为雷达天线增益设定,λ为波长,σ为目标的雷达截面积,Smin为最小可检测信号的功率。式(1)中给出了雷达各参数与作用距离的定量关系,但并没有考虑雷达在正常工作状态下因环境因素带来的损耗和误差。
对于雷达而言,σ和Smin在实际中不可准确估量,但对于参数化波形建模来说,并不需要考虑雷达的实际损耗和不可估量的因素,只需对雷达可控制的参数进行分析建模。而一般情况下雷达发射最大功率一定,发射增益则与雷达天线设置有关,接收机增益一般可控,雷达工作波长则在雷达前期论证时已经确定。则
s(t)={NStc;}
(2)
式(2)中,NStc为雷达的接收增益曲线编号,可对雷达的不同距离段的接收增益进行控制。
2.2 雷达波形分析
雷达发射信号通常为窄带信号,用复信号可表示为
st(t)=u(t)ej2πf0t
(3)
其中,u(t)为信号的复包络,f0为载频。
u(t)=a(t)ejψ(t)
(4)
a(t)为信号的幅度调制,ψ(t)为信号的相位调制项。
对于线性调频矩形脉冲信号,其信号的表达式为
(5)
其中,T为脉冲时宽,μ=B/T为调频斜率,B为调频带宽。
对于信号接收后的处理过程来说,还需要考虑采样率、频域脉冲压缩时FFT的点数、加窗方式等参数,才可完整地表述一个信号的接收处理过程。
因此,对于一般信号,可对其参数化为
s(t)={T;B;f0;fshift;fs;P;W;}
(6)
其中,fshift为频偏,采用频偏则是为了提高雷达抗干扰能力,fs为采样率,P为脉压方式,其中可包含脉压方式、脉压点数等参数;W为加窗方式。雷达通过DDC、数字采样等技术,对以上参数进行集成控制,可表示雷达的波形发射与处理的过程,通过改变其中的参数,可改变雷达的不同发射与接收配置。
2.3 时域参数分析
普通脉冲多普勒雷达是通过测量发射信号传播到目标并返回来的时间来测定目标距离的。雷达对于时域的控制参数可影响到雷达的探测距离、脉冲发射盲区、距离分辨率。一般情况下,在发射信号的PRF确定时的最大不模糊距离为
(7)
其中,fr为雷达的脉冲重复频率。因此,雷达的脉冲重复周期决定着雷达的最大不模糊距离,在进行雷达设计时,应使其满足雷达的工作需求。在对其进行控制时,可实时改变雷达的最大不模糊距离,适应其工作模式需求。同时,雷达一般采用多脉冲的发射方式,可控制其脉冲重复数,用Np表示。
对于雷达接收来说,为充分利用雷达前端和处理资源,可设置AD采样起始时间、AD采样波门宽度这两个参数,分别用TADS和TADG表示,控制雷达前端AD采样的开始与结束时间;设置接收起始时刻和接收波门宽度,分别用TST和TGW表示,可控制雷达后端处理的起止时间。在对参数进行设置时,应充分考虑雷达信号脉宽、雷达作用距离、雷达最大不模糊距离等因素,结合雷达具体需求,对参数进行控制。综上,雷达时域参数可描述为
f(t)={TPRI;NP;TST;TGW;TADS;TADG}
(8)

图3 雷达发射接收时序图
2.4 空域参数分析
方向图用于描述天线阵列产生的电磁场及其空间内能量分布的情况。其具有指向性,可理解为对相控阵雷达天线辐射的方向性描述[9]。对于平面相控阵天线来说,其水平放置的阵元如图4所示。各个天线单元排列在平面内的矩形栅格内,整个阵面在XY平面上,共有M×N个天线阵元,单元间距分别为d1和d2,方位角为φ,俯仰角为θ,当天线均匀照射时,其方向图函数为
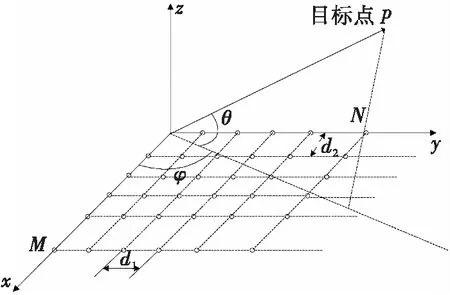
图4 雷达阵元分布图
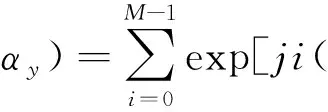
(9)
其中:κ=2π/λ,为波数。
cosαx=cosθcosφ
cosαy=cosθsinφ
(10)
当波束指向为阵列法线方向,即ΔφBα=ΔφBβ=0时,平面阵列的幅值方向图函数可表示为式(11)。

(11)
通常情况下,雷达为了更好地实现两位相扫,平面相控阵将天线的各个阵元垂直排列在yoz平面内,如图5所示。

图5 雷达阵列垂直排列
与式(11)相同,可得到其方向图函数为

(12)
其中ΔφBα与ΔφBβ分别表示z轴和y轴方向内的阵内相位差。
一般雷达中阵元数与阵元间距固定,波数与波长相关,则方向图与俯仰角θ和方位角φ相关。通过控制这两个参数,可控制波束指向与雷达方向图参数。
雷达在进行波束扫描时,可赋予雷达初始的方位俯仰指向和期望的方位俯仰指向,则可描述雷达波束扫描过程,即雷达空域扫描参数可表示为
f(s)={SIA;SIE;SEA;SEE}
(13)
其中,SIA、SIE为雷达初始方位与俯仰指向,SEA、SEE为雷达的期望方位与俯仰指向。
对于数字阵列雷达,雷达整个阵面的波束结构、波束赋形又可由用户自由定义,因此,对雷达波束的具体描述可表示为
f(b)={BBS;BFX}
(14)
其中,BBS为雷达的波束结构参数,BFX为雷达的赋形参数,可由用户自行定义,从雷达参数库中调用。
综上,认知雷达的参数化波形可描述为
s(t)={T;B;f0;fs;P;W;TPRI;
NP;TST;TGW;TADS;TADG;
SIA;SIE;SEA;SEE;BBS;BFX}
(15)
其中,脉压方式、波束结构、赋形参数可预先设置雷达参数库,当系统需要根据环境配置新的参数化波形时,可仅仅配置其在库中的编号即可,雷达则根据编号从库中读取具体参数。
3 仿真验证
3.1 信号频域仿真
对于雷达发射信号,信号形式取线性调频信号,参数取T=100μs,认知雷达采用DDS,雷达进入前端之前信号通常采用零中频,取B=2MHz,f0=-B/2,fshift=5MHz,fs=10MHz,发射信号仿真如图6所示。
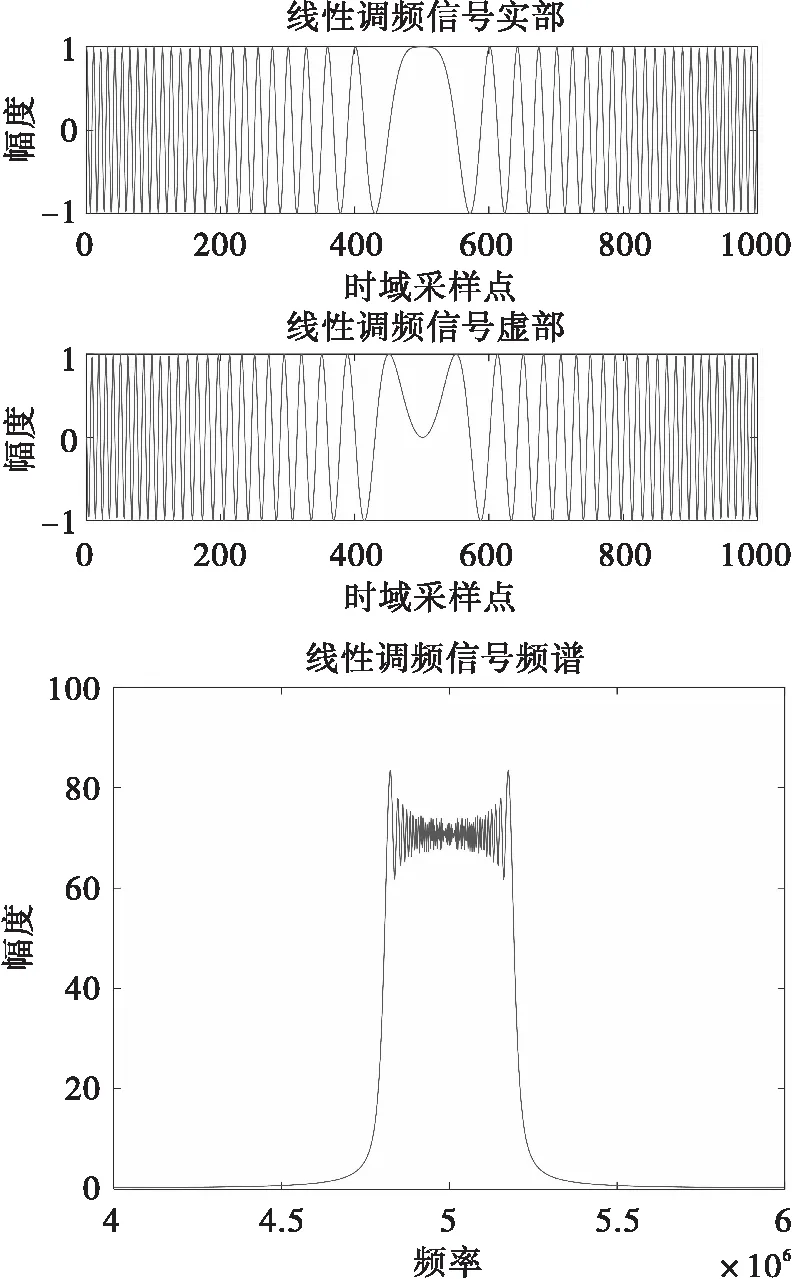
图6 信号1仿真结果
对于认知雷达来说,发射一种波形很难满足雷达对于不同距离段、不同任务的探测需求,则可再配置一种波形参数,满足雷达近区探测需求和抗干扰需求,其参数可设置为:T=50μs,B=2MHz,f0=B/2,fshift=-5MHz,fs=10MHz。
对于接收处理,脉压方式P=1,脉压方式为雷达系统自行定义,可包含脉压方式和脉压点数等参数。本文仿真中,当脉压方式为“1”时,脉压方式为频域脉压,脉压点数为2048点,目标距离R=20km,RCS=1,信号1的回波信号及脉压结果仿真如图7和图8所示。

图7 回波信号仿真图

图8 回波信号脉压结果
根据接收回波的结果分析,目标在20km处,可根据目标距离对雷达下次发射的波形进行自适应选择。其参数可设置为:
信号1:T=20μs,B=2MHz,f0=B/2,fshift=5MHz,fs=10MHz,仿真图如图9所示。

图9 信号1 仿真结果
信号2:T=20μs,B=2MHz,f0=B/2,fshift=-5MHz,fs=10MHz。
同时也应根据回波信号对雷达的发射时域参数和空域参数进行自适应选择。本文着重于对认知雷达参数化波形的参数类型进行设计,不再对认知雷达的认知算法及调度后的参数选择进行深入研究。
3.2 时域仿真
时域上,取TPRI=1000μs,NP=10,根据处理时间,取TST=152μs,TGW=750μs,TADS= 150μs,TADG=850μs,一个脉冲内发射两个码片,其时序图如图10所示。

图10 雷达时序图
3.3 空域仿真
在空域上,方位俯仰维阵元数都为8,取SIA=0,SIE=0,SEA=30,SEE=30,方向图扫描范围为-30°~30°,方向图仿真结果如图11所示。

图11 雷达方向图
4 结束语
认知雷达是雷达向更加智能化发展的必要阶段,对其参数化波形进行研究设计,可有效推动认知雷达的发展。参数化波形可有效对雷达资源进行表征描述,本文对参数化波形进行设计,有效建立起一种全面的参数化波形,对雷达各部分资源进行表征描述,可供雷达进行调度,对雷达资源调度和波形库的建立有帮助意义,提升雷达的灵活性和可重构性。

