一种六旋翼无人机的多模型容错控制方法*

徐雪松，倪 赟，吴仪政

（华东交通大学电气与自动化工程学院，南昌 330013）

0 引言

多旋翼无人机具有体积小、运行维护成本低、机械结构简单等诸多优点，近年来被广泛应用于军事及民用领域。无人机在军事领域主要用于远距离侦察；在民用领域主要用于航拍、森林火情监测、替代人力进行电力线路巡检、携带设备进行科研工作等等。随着无人机运用范围的扩展，其工作环境也变得更为复杂多样，尤其是在一些环境恶劣的地区，发生故障的概率大大增加，严重时可能会造成无人机及其携带设备的坠毁，造成不必要的经济损失。因此，在无人机发生故障时如何保持稳定飞行和安全降落成为国内外专家学者重点研究方向。

相比四旋翼无人机，六旋翼无人机存在结构冗余，为单个电机故障下的容错控制提供了机械基础。文献［6］针对电机故障采取将故障电机及对角电机关闭的极端处理方式，这种处理方式将无人机的负载能力降低了三分之一。文献［7］针对执行器故障设计了参考模型与加权伪逆分配相结合的控制器，能实现多个电机同时故障下的容错控制，但是没有考虑到伪逆法处理故障下电机转速分配，存在超出电机约束上限问题。

以上提出的容错控制方案都是针对标准旋翼转向布局的无人机，但近年来有研究表明，该类无人机在容错可行性方面存在一定的缺陷。文献［8］通过构造可达控制集，提出评估多旋翼无人机在电机故障下的静态可控性方法，表明了旋翼转向布局对容错性能有很大的影响，标准旋翼布局的无人机在单个电机故障情况下会丧失对偏航的控制。文献［9］提出了可用控制权限索引（ACAI）来量化无人机的可控性，通过计算和理论分析得出无人机在电机故障下的可控性，结果表明，一种新型旋翼转向布局（PPNNPN）的无人机在其中4 个电机分别发生故障时依然能保持良好的可控性。

基于上述分析，本文以PPNNPN 型六旋翼无人机为研究对象，解决电机转速存在上下限约束时，单个执行器发生完全失效故障下的稳定控制问题。

本文利用迭代修正算法克服伪逆算法无法解决电机转速限制的缺陷，并利用交互多模型算法实现对应控制效率矩阵的调用，通过在线调整剩余电机的输出，实现容错飞行。

1 建立数学模型

1.1 无人机模型

图1 为PPNNPN 型六旋翼无人机简化结构示意图，1 号和2 号电机顺时针旋转，3 号和4 号电机逆时针旋转，5 号和6 号电机分别为顺时针旋转和逆时针旋转。

图1 六旋翼无人机简化结构示意图

根据牛顿欧拉方程建立无人机的数学模型：

式中，B 为控制效率矩阵，与无人机的结构有关；ω表示第i 号电机转速，其上下限为ω和ω。

本文的研究对象为“十字型”PPNNPN 六旋翼无人机在单个电机完全卡死或螺旋桨完全断裂等极端故障下的容错控制，表现为故障执行器的升力和力矩输出为0，为了方便研究，故障的影响通过控制效率矩阵表示。考虑引入故障系数η，控制效率矩阵可以表示为：

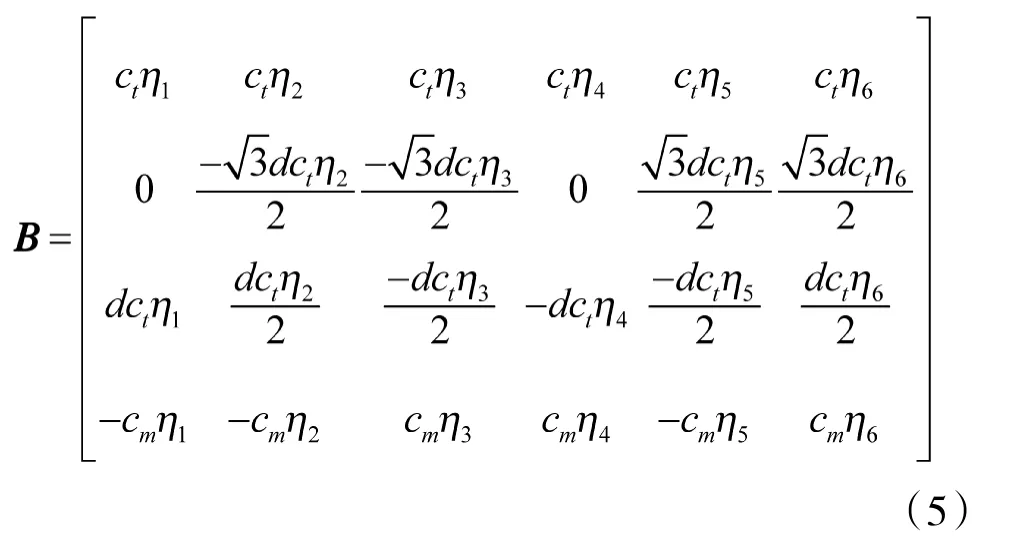
式中，c表示升力系数；c表示拖拽系数；d 为电机到无人机质心距离；η∈［0，1］（i=1，2，…，6），当η=0 表示i 号执行器发生完全失效故障，η=1 表示执行器正常工作。其控制效率矩阵包括7 种，分别为6种不同故障和1 种正常工作情况。

1.2 电机模型

无人机执行器主要由无刷直流电机、螺旋桨以及电调组成，其被控过程为无人机在收到虚拟控制指令后，通过控制分配矩阵解算出各个旋翼转速的大小，随后通过电调输出占空比为σ 的PWM 信号，无刷电机在接收到PWM 信号后输出相应的转速进而实现无人机姿态控制和垂直起降。电机的一阶惯性环节的传递函数可以表示成：

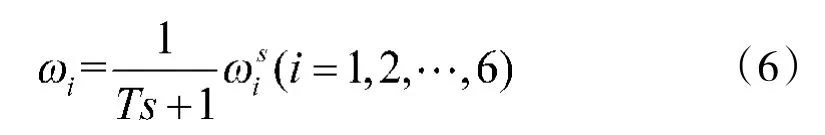
式中，ω表示第i 号电机的瞬时转速，T 表示电机的惯性时间常数，ω表示第i 号电机的稳态转速。稳态转速与电调输出的PWM 信号满足如下线性关系：

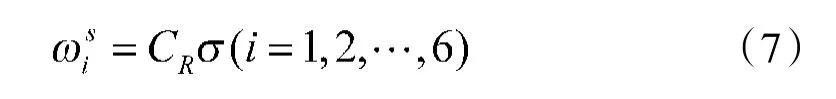
式中，C为PWM 信号与转速的比例系数。

2 迭代修正控制分配设计

针对容错控制器，采用分层设计结构，包括基本控制律和控制分配律。PID 控制器设计简单，算法成熟，被广泛应用于飞控。因此，将文献［11］中的串级PID 控制算法作为本文的基本控制律。

在无人机的转速分配问题中，主要是对式（2）进行求解，通常是运用伪逆法，这种方法能很好的解决无故障时的飞行控制，但是当发生故障时，无人机的控制分配还要受到电机转速上限的约束，此时，利用伪逆法会出现在约束范围内无解的情况。针对这一问题，本文在利用伪逆法进行初步求解的基础上，对超出电机转速约束的解进行修正，使得分配结果既满足范数最优同时又满足执行器约束。具体修正步骤如下：

Step 1：采用伪逆法对式（2）进行初步求解：

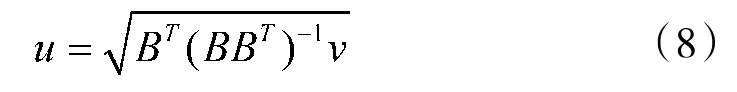
Step 2：对式（8）中的每个电机转速ω进行判断，若满足式（4），则不进行处理；若超出约束范围，则令超出约束的解为ω=ω或ω=ω，在约束范围内的解保持不变；

至此，通过最大化剩余正常电机的利用率解决了部分电机转速超出约束的问题。

3 故障诊断设计

交互多模型（Interacting Multiple Model，IMM）算法能够对多个模型同时滤波，并能对各个模型的概率进行调整，具有准确性高、速度快等优点，被广泛应用于机动目标的定位跟踪，但在故障诊断方面应用较少。考虑到故障诊断的准确性和快速性是容错控制的前提，而六旋翼无人机的故障模型较多，通过观测器进行故障诊断与定位消耗时间较长，因此，本文考虑将IMM 算法运用于故障诊断。与IMM 算法在目标跟踪问题的应用不同，本文设计了一个故障检测阈值，通过判断各模型的概率是否大于设定的故障检测阈值来确定故障的位置。图2为IMM 算法应用于故障检测的原理图：

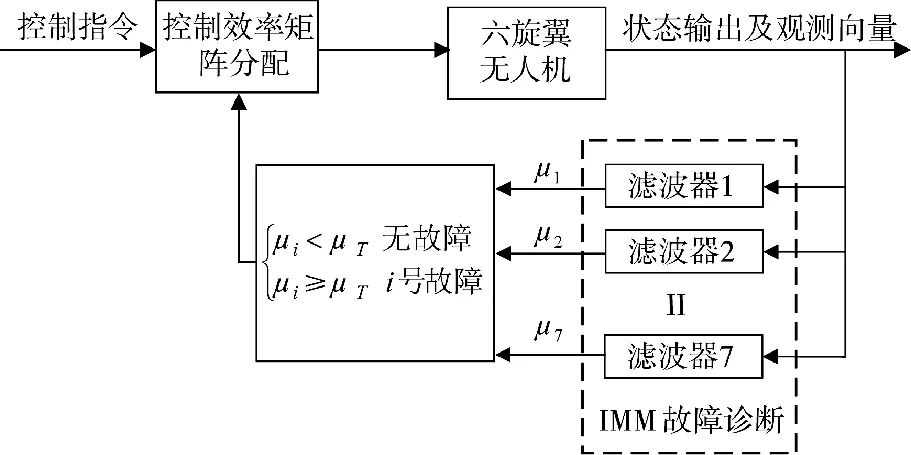
图2 IMM 故障诊断原理图

IMM 算法每次循环包含以下4 个步骤：输入交互，并行滤波，模型概率更新和融合输出。具体步骤如下：

Step 1：建立模型集

其中，U为控制输入量，w，v为过程噪声和观测噪声，均为零均值和协方差为Q 和R 的高斯白噪声。

对式（9）线性化，得到系统离散线性状态方程：

Step 2：输入交互

在进行滤波前，先设计模型概率转移矩阵P，矩阵元素P表示第i（i=1，2，…，7）个模型到第j（j=1，2，…，7）个模型的概率。输入交互设计如下：

k 至k+1 时刻的预测模型概率：

k 时刻模型i 到j 的混合概率：

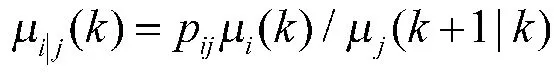
k 时刻的混合状态估计：

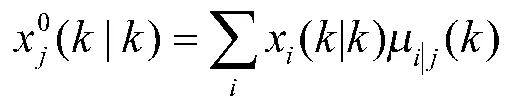
k 时刻的混合协方差：

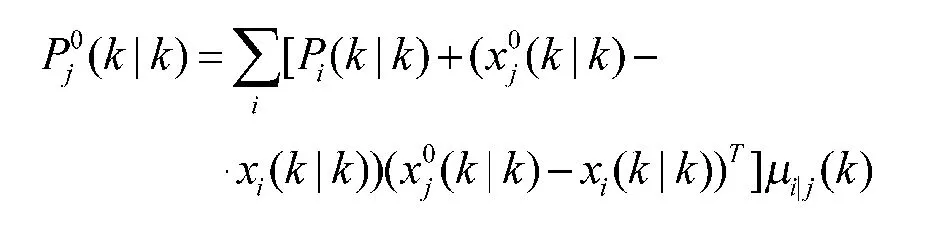
Step 3：模型并行滤波

k 至k+1 时刻的预测状态：

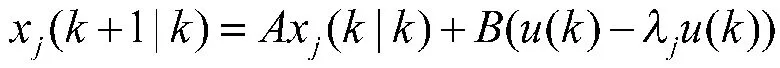
k 至k+1 时刻的预测协方差：

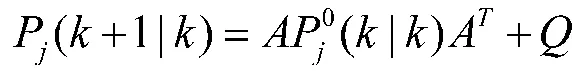
k+1 时刻的测量残差：

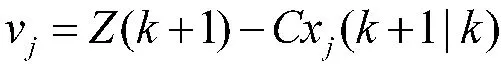
k+1 时刻的残差协方差：

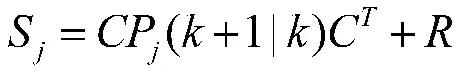
滤波增益：

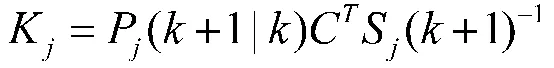
k+1 时刻的状态更新：

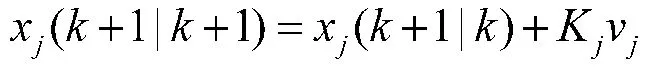
k+1 时刻的协方差更新：

Step 4：模型概率更新

似然函数：

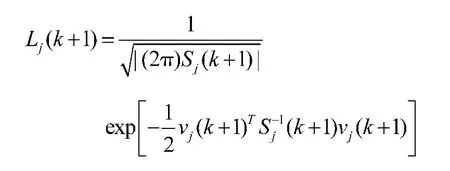
模型概率：

Step 5：交互输出

总的状态估计：

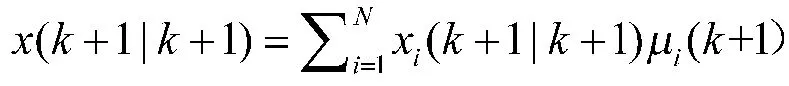
总的协方差：

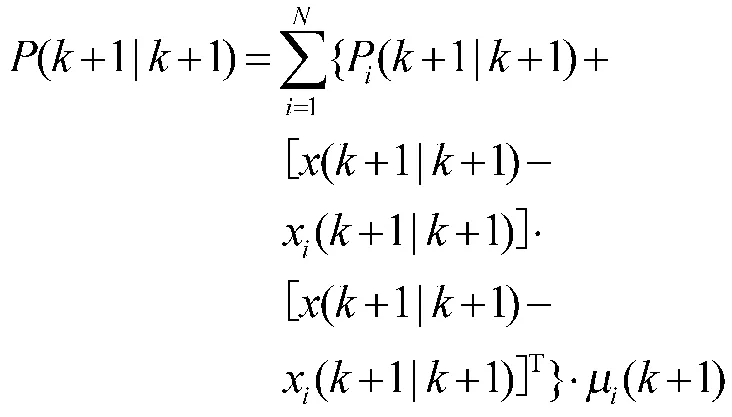
Step 6：故障诊断结果

判断模型概率向量中最大值与故障检测阈值μ的关系：

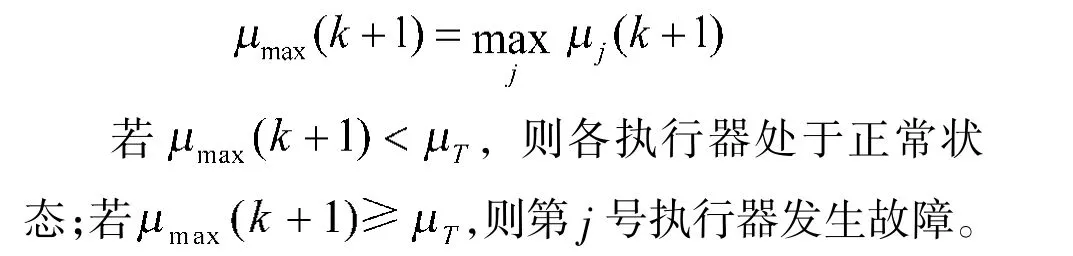
4 仿真结果

4.1 仿真参数

为了验证设计的容错控制策略的有效性，在MATLAB/Simulink 环境中建立模型并进行数值模拟仿真。无人机模型仿真参数选取如下：

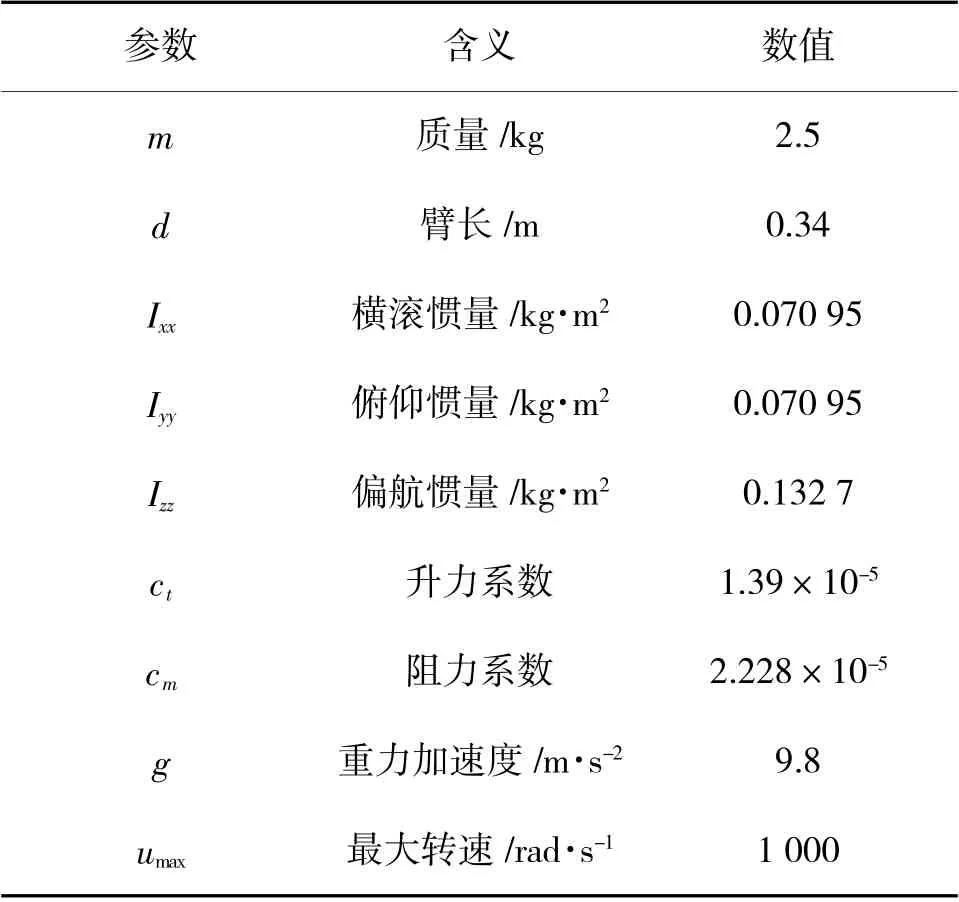
表1 六旋翼无人机参数

4.2 仿真实验及结果分析

本文研究的PPNNPN 型六旋翼无人机在1、2、3、4 号执行器分别发生故障时，能实现姿态完全可控，而对于5、6 号执行器故障，通过舍弃偏航实现容错控制，因此，本文分别对两种情况进行仿真。

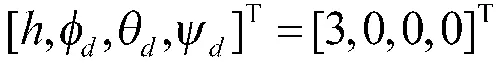
针对不完全可控情况，本文舍弃对偏航方向的控制，以牺牲部分性能为代价，通过控制滚转和偏航角使无人机能够稳定降落，以5 号电机为例，进行仿真实验。设定无人机悬停在离地面高度为3 m处，在第20 s 时，令5 号电机故障，并在第40 s 时发出降落指令。

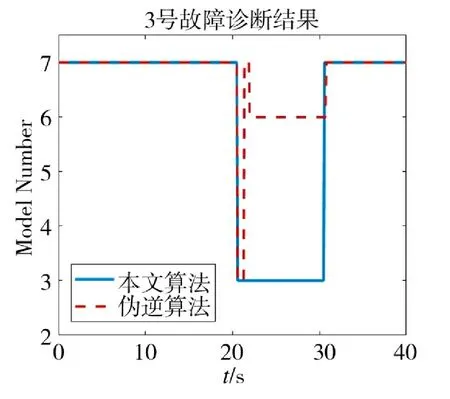
图3 3 号电机故障诊断结果

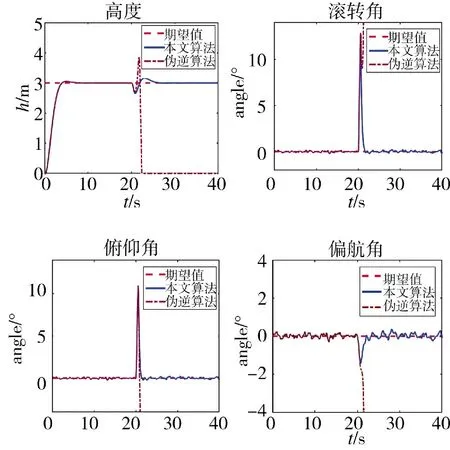
图4 3 号电机故障时的姿态控制

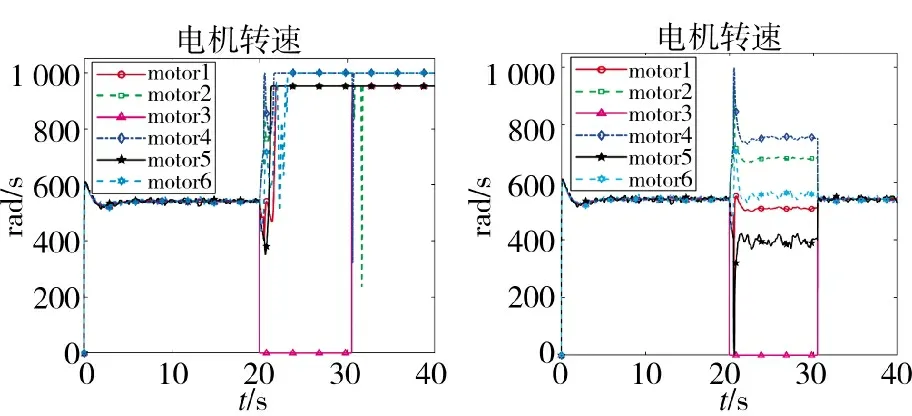
图5 3 号电机故障时的转速分配

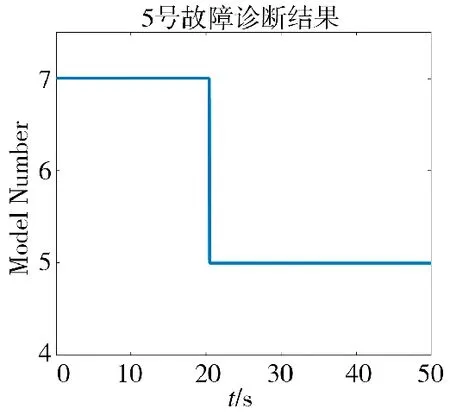
图6 5 号电机故障诊断结果

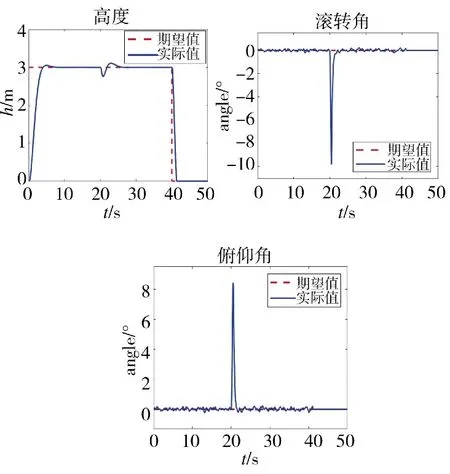
图7 5 号电机故障时的姿态控制

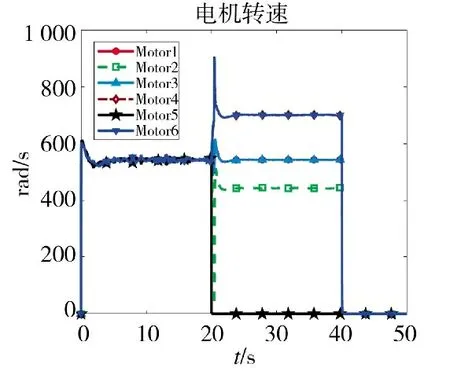
图8 5 号电机故障下的转速分配

为了充分说明本文算法的有效性，在3 号电机故障时分别运用伪逆法和本文的迭代修正法进行仿真。图3 表示3 号电机故障时，本文算法和伪逆法分别作为控制分配算法时，交互多模型故障诊断结果，数字7 表示正常运行，数字6 表示6 号电机故障，以此类推。可以看出，在前20 s 无人机处于无故障状态，伪逆法和本文算法都能很好地处理无人机控制问题，因此，运用两种算法进行控制分配时诊断出故障的时间相同，均为20.5 s，并且本文算法能在30.4 s 时准确诊断出无人机恢复正常，而伪逆分配法则出现了误诊断的情况，这是因为在故障时，伪逆法无法解决控制分配问题，无人机失控导致状态变化大影响故障诊断效果。图4 为3 号电机故障下，分别运用本文算法和伪逆法时，无人机对于期望姿态的跟踪情况，由图4 可以看出，无人机姿态跟踪过程存在一定的波动，这是由于外界干扰导致的；在前20 s，两种算法都能很好地跟踪期望姿态，但是当发生故障时，本文算法能够快速调整无人机姿态，使飞行保持稳定，而伪逆法则出现了失控现象。图5 为在两种算法下电机转速分配的情况，可以看出，在前20 s 两种算法对于转速的分配相同，而在发生故障后，由于本文限制最大转速为1 000 rad/s，运用伪逆法使转速达到最大值且无法进行改正，最终导致失控，而本文算法能够在部分电机转速达到最大值时通过增大其他电机的使用率，使无人机快速调整实现容错控制。

针对5、6 号电机故障，由于舍弃了对偏航的控制，式（2）少了一个约束，因此，解的范围更广，这就使得本文算法和伪逆法都能适用，因此，针对5 号故障，只采用本文算法进行仿真。仿真结果表明，5号电机故障下，本文算法能控制无人机实现对高度、滚转角及俯仰角的跟踪，并能控制无人机稳定降落，实现了容错控制的目的。

5 结论

本文针对PPNNPN 型六旋翼无人机电机完全失效故障问题，提出了一种迭代修正控制分配方案。在无人机飞行时，利用交互多模型滤波器对无人机的飞行状态进行实时在线监测，并将结果反馈给控制器，在基本控制器保持不变的情况下，通过调用对应的控制效率矩阵并进行控制分配解算，实现容错控制。仿真结果表明，该方法能够有效解决故障下电机转速分配问题，具有良好的容错效果。今后将对控制算法进一步优化，并考虑不同结构的多旋翼无人机，以实现所有旋翼故障情况下均可控的目标。