纽结的Alexander 多项式的微分性质

韩友发，王泓月，燕佳钰，孙思宇

纽结理论是拓扑学的重要组成部分，并且得到了广泛地应用.在纽结研究中，对纽结进行等价分类是首要任务.若要进行分类首先要找到同痕不变量，同痕不变量要满足计算方便的特点，纽结多项式发挥了重要作用，纽结多项式包括Jones 多项式[1］、Alexander 多项 式[2］、Conway 多项式[3］和Homfly 多 项 式[4］等.而多项式的微分性质也与纽结不变量的性质有着非常重要的联系，在文献[5-7］中，对n个分支的环链的Jones 多项式及Homfly 多项式一阶、二阶至k阶微分的整除性质进行了讨论，其中系统地阐述了按Hopf 环链方式将两个至n个平凡纽结进行结合形成的链环Homfly 多项式各阶微分的多样性质，除此之外，还有学者描述了对三叶结进行Hopf 链接的Jones 多项式求高阶微分会有怎样的结论，得出了Conway 多项式的微分相关结论，总结了该多项式的几种重要特性；同时对两个分支n个交叉点的环链Alexander 多项式的一阶、二阶至高阶微分在变量取得某一特定值时与环链的环绕数之间的关系进行了总结，初步探索了多项式高阶微分性质与环链本身几何性质之间存在的关系，而文献[8］则对定向链环的Alexander 多项式的高阶微分中当变量t=1 的情况进行了研究.以上研究分别从规定的某种纽结的一种或多种多项式的低阶微分出发，最后将结论推广到高阶微分，主要研究了微分的整除性质和变量特殊取值时的性质.

本文共分三部分，第一部分是预备知识，给出了纽结和链环的具体定义和相关性质.同时还对多种纽结多项式的基础知识进行了系统地介绍.第二部分计算了Twist 纽结、n个Twist 纽结做连通和的Alexander 多项式的k阶微分，从而得到其整除性质.进而对任意纽结的Alexander 多项式的各阶微分进行了计算.第三部分对文章内容进行了总结.

1 预备知识

定义1 在三维欧式空间R3中，若有一子空间K同胚于圆周S1，则称K是一个纽结.纽结是三维欧式空间R3中连通且不自交的闭曲线.若给纽结规定一个方向，则称该纽结为有向纽结.

定义2 对于空间Rn中的一个子集L，若L与多个球面的不交并Sp1⋃Sp2⋃…⋃Spr是同胚的，则称L是有r个分支的环链.

定义3 若有性质经过Reidemeister 变换和平面移动仍不变，则该性质称为纽结的同痕不变量.

引理1[8］存在一个对应Δ，给每一个有向投影图L联系上一个变量为t的多项式Δ（L，t），满足以下三个条件：

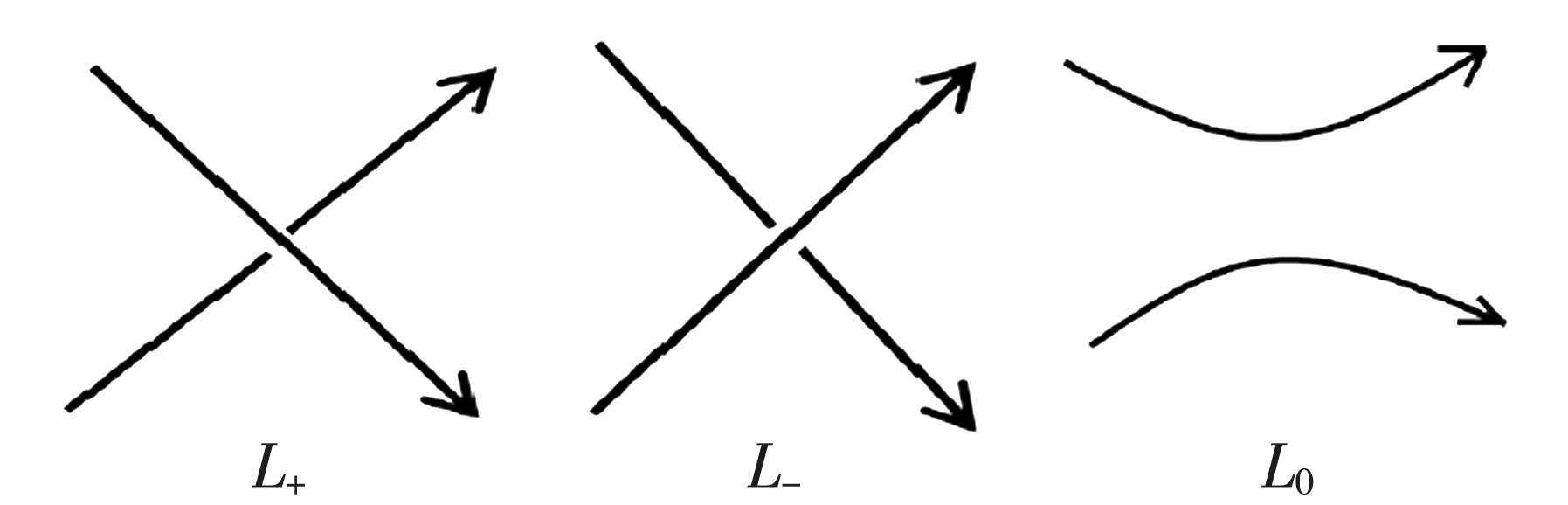
图1 三个除了该交叉点外完全相同的投影

（3）标准值.平凡纽结所对应的多项式为Δ（Ο）=1.

则称Δ(L,t)为L的Alexander 多项式.

如图2 所示的为Twist 纽结的一般形式，通常记为Tp，p是扭转部分的交叉点数，Twist纽结的特殊形式为三叶结及8 字结.

图2 Twist 纽结

如果一个纽结能被分解成都不是平凡的两个纽结，则称这个纽结是一个复合纽结.类似于乘法的因式，分解得到的两个纽结称为复合纽结的因子纽结，若一个纽结不能再分成另外两个纽结的和，则称这个纽结为素纽结[9］.根据Alexander 多项式的定 义 很容易得到如下结果.

引 理2 若纽结L1和L2的Alexander 多项式分别为Δ(L1)和Δ(L2)，则有

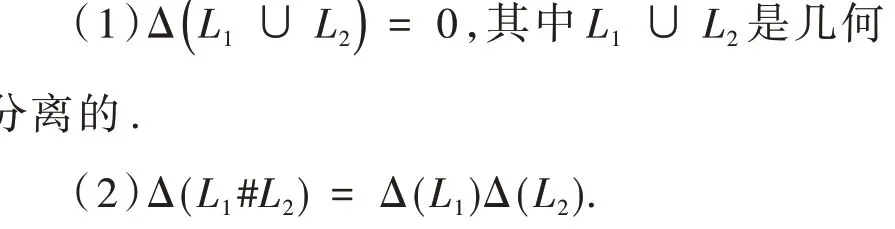
2 一些纽结和链环的Alexander 多项式的高阶微分

引理3[10］Twist 纽结的Alexander 多项式为

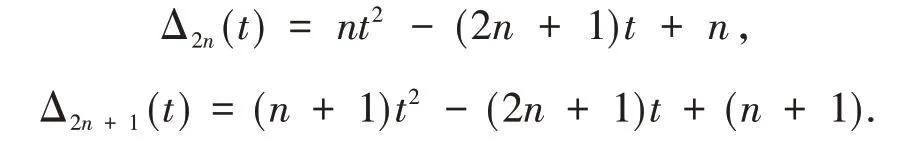
引理4 Twist 纽结的Alexander 多项式的k阶微分在t= 1 时能被k!整除.

根据引理3 直接计算可证明该结果.

引理5 若L是两个Twist 纽结的连通和，则它的Alexander 多项式的k阶微分在t= 1时能被k!整除.

证明 两个Twist 纽结进行连通和有三种类型如下：

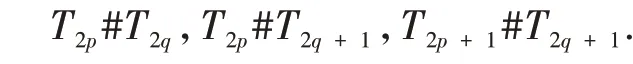
现给出第二种类型的证明，其他同理可证.

由引理2 及引理3 可知

从而结论成立.

同理当k= 3，k= 4 时，将t= 1 代入，分别是6(p-q- 1)和24(pq+p)，所以结论成立.

综上三种情况，在k≤4 时引理成立，而在k＞4 时三种情况的高阶微分均为零.

定理1n个Twist 纽结的连通和的Alexan⁃der 多项式的k阶微分在t= 1 时能被k!整除.

证明 当n= 2 时，由引理4 可知结论成立；

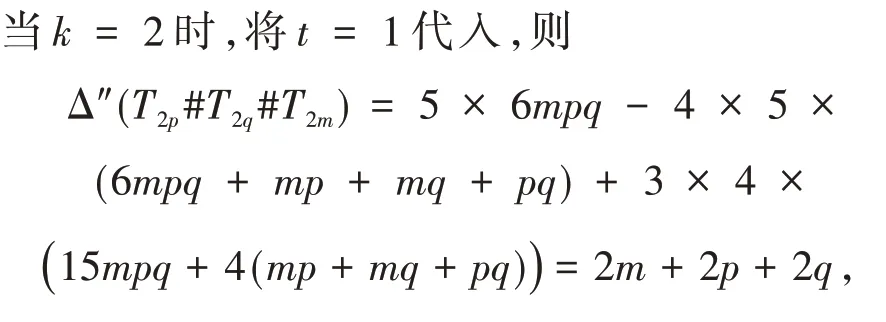
其中：m、p、q均为整数，所以该式能被2!整除.

该式能被5!整除，其他情况类似证明，并且当k＞6 时各阶微分均为零，从而当n= 3时结论成立.

当n＞3 时，若n= 2i，则可看作是i个“2个Twist 纽结的连通和”做连通和，对n= 2 时结论成立，由连通和Alexander 多项式的性质可知对n= 2i结论成立.若n= 2i+ 1，则可看作是1 个“3 个Twist 纽结的连通和”及2(i-1)个“2 个Twist 纽结的连通和”做连通和，对n= 2 及n= 3 时结论成立，从而可知对n=2i+ 1 结论成立.

综上所述，对任意n个Twist 纽结的连通和的Alexander 多项式的k阶微分在t= 1 时能被k!整除.

注：n个Twist 纽结的连通和的Alexander多项式的k阶微分在k＞2n时均为零.

定理2 任意纽结L的Alexander 多项式的高阶微分V(k)(L,t)为：

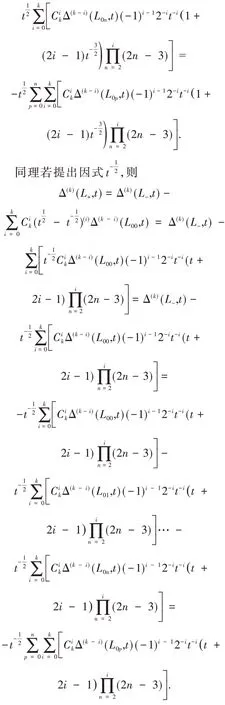
综上所述，任意纽结的Alexander 多项式的高阶微分为：

注：根据这个结果和方法可以讨论在某些点的微分性质.

3 结语

研究纽结多项式的微分性质将有利于讨论纽结不变量和三维流形不变量的性质，特别是Conway 多项式的系数和纽结不变量有着密切的关系，它揭示了很多拓扑性质.本文研究了Alexander 多项式的高阶微商性质，给出了比较深刻的刻画.同时计算了Jones 多项式的高阶导数的计算公式，为今后对这方面的研究提供了一个方法.