微小卫星交会对接位姿测量中合作目标设计方法

张 刘， 张 文， 王亚明， 吕雪莹， 王文华

(吉林大学 仪器科学与电气工程学院，吉林 长春130012)

1 引 言

由于微电子、新材料和新能源技术的发展，微小卫星已成为航天活动中的新兴方向[1-2]。与传统卫星相比，微小卫星具有研制周期短、成本低、发射灵活等特点，在星座技术、编队飞行、在轨组装中具有突出优势。交会对接技术是在轨服务活动中的核心技术，由于微小卫星自身尺寸与电源功率约束等原因，致使传统微波雷达或激光雷达等载荷因其体积大、功耗高，难以应用在微小卫星平台上。而视觉测量方式则因其结构简单、精度高、信息量大与功耗低的优势，成为微小卫星在轨服务活动中相对位姿测量的主要方式[3-4]。

视觉测量方式是指通过安装在追踪星上的光学相机来识别目标星上的合作目标或非合作目标，以完成追踪星与目标星之间的相对位姿解算[4-5]。为保证微小卫星成功交会对接，常在目标星上安装合作靶标作为合作目标[6-7]。

在远距离靶标设计方面，Bodin等人设计一种在轨实验台[8]，利用不同波长激光照射后的图像相减得到靶标标志点，实现位姿测量。由于激光的高方向与高亮度特性，当卫星摆动时，导致测量误差增大。Lecroy等人设计了一款基于激光的导航目标[9]，具有一定的离轴效应，增加了算法难度。北京航空航天大学的Pan等人设计了6个LED靶标[10]，适用距离为0.5 ～20 m,且在0.5 m处测量精度为10 mm。

在近距离靶标设计方面，温卓漫[11]研究一种立体式无源合作靶标，可在0.3～1.5 m的距离内使用，实现六自由度的高精度三维空间定位，其作用距离短，精度高。吕耀宇[12]提出一种平面式无源靶标设计方案,并对靶标的编码信息和尺寸进行了设计。王保丰等[13]设计了两种圆形编码靶标，并对靶标进行识别，其适用于太阳光下的识别。但在不同时刻，因太阳光强、光照角度不同，导致靶标识别过程复杂。杨进[14]等对根据靶标图像如何判断相对运动状态进行分析，然而需要航天员手动控制交会对接，限制了其适用场景。

现有的关于视觉测量中合作目标研究，集中于近距离或中远距离。然而，在实际应用中，视觉测量整个过程均需要对合作目标进行识别，因而现有设计具有一定的局限性，即只能在近距离或中远距离使用。本文通过对合作目标参数进行分析与设计，实现了从远至近均可被相机识别的合作目标设计。首先，本文对合作目标模型进行简化，并对靶标特征点进行个数与大小设计。之后，根据相机参数与合作目标的互相约束进行合作靶标尺寸设计。然后，对特征点位置进行确定，基于仿真图像对合作目标引起的位姿姿态测量误差进行分析。最后，通过仿真和试验进行分析与验证。

2 双星交会对接测量方案

以双星稀疏孔径成像在轨组装视觉测量为研究背景，在此背景下，实现在微小卫星大视距对接情况下的相对位姿测量。考虑到卫星交会对接在轨运算效率和目标识别稳定性，需选用远、近场两台相机来获取目标信息。利用目标的位置与空间约束等已知信息，以求解相机和目标间的相对位姿。任务过程如图1所示,目标星在轨道运行，其上有合作目标以供识别，相机安装在追踪星上，对

合作目标进行识别，以测量出双星的相对位姿，为交会对接任务提供数据。

3 合作目标简化模型建立

考虑到空间光照条件与交会对接过程中卫星之间的相对运动，实时的合作目标模型难以精准建立，因此，本文根据目标特征点的形状大小和位置分布，建立了合作目标的简化模型，主要分析合作目标特征参数对单目相机成像效果与对相对位姿测量精度的影响。

3.1 合作靶标能源选择

合作靶标根据是否消耗能量分为有源靶标和无源靶标。其中，无源靶标仅在可见光条件下才能正常使用，且会因不同光照角度、光强的不同，产生过曝或过暗情况，导致无源靶标成像效果不一，影响位姿解算的结果；有源靶标采用发光二极管或激光作为光源，在近距离时因光源散射导致特征点重合，难以进行识别，因此，适合在中远程距离使用。

本文设计靶标为大视距情况下，在无太阳窗口条件下使用，无源靶标难以应用。因此，本文采用有源发光式设计，选用发光二极管作为整个靶标的背景光源。

3.2 合作目标特征点个数确定

相对位姿解算是通过特征点在图像上的二维坐标与空间三维坐标来解算靶标与相机之间的相对位姿关系，亦称之为PnP问题。目前,常用算法包括直接线性变换法、EPnP法、P3P算法等。其中直接线性变换法解算位姿，需要6个特征点来求解出旋转矩阵和平移矩阵。EPnP算法需要4个不共面的特征点来求解位姿,考虑靶标尺寸及高度限制。本文选用P3P方法求解相对位姿。

P3P位姿测量原理如图2所示，A～E为不共线三维空间点，a～e为图像投影点，P为相机坐标系中心点，W为世界坐标系，T为合作靶标坐标系。根据余弦定理可知：

(1)

将式(1)进行消元替换可得：

(2)

其中：

图2 P3P位姿解算原理示意图Fig.2 Schematic diagram of P3P pose calculation principle

通过对式(2)进行分解，得出4种特征点相对于相机坐标系的相对位姿关系[15-16]。为得到唯一正确位姿结果，需要第4个特征点进行验证并求出唯一解。考虑在特征点形状大小相同且对称排列时，难以判断合作靶标的旋转情况，同时考虑设计的冗余性，本文选定5个非对称排列的特征点，以便于后续的识别定位。

3.3 特征点尺寸设计

在大视距对接情况下，由于测量距离变化大，致使单个相机或单组特征点难以满足整个对接过程中的测量需求。应选取远、近场两款相机，并分别设计远距离、近距离两组不同特征点。

追踪星上远距离相机焦距为35 mm，工作距离为1.5～100 m；近距离相机焦距为12 mm，工作距离为0.1～1.5 m。两款相机的图像传感器分辨率均为1 280×1 024，水平和竖直像元尺寸均为5.3 μm。根据相机视场角计算公式(式(3))，确定远距离相机水平视场角为11.07°，竖直方向视场角为8.86°。近距离相机水平视场角为31.56°，竖直方向视场角为25.48°。

FOV=2arctan[xres·u/2f]，

(3)

式中：FOV为相机视场角，xres为传感器分辨率，u为像元尺寸，f为相机焦距。

根据视场角与相机工作范围，本文设计靶标的最大尺寸为200 mm×260 mm。物体在传感器所占像素计算公式如式(4)所示：

(4)

式中：u为像元尺寸，xres为传感器分辨率，f为相机焦距,W为物体的尺寸，d为物体和相机的距离。计算出不同物距下特征点直径如表1所示。

表1 不同物距下特征点直径

由表1可知，当选用的远、近场相机焦距为35 mm和12 mm，特征点大小分别为40 mm和4 mm时，在远、近场相机最大工作距离，特征点至少占据3×3像素，且特征点成像位置不重合。在远、近场相机最小工作距离，远、近距离靶标都在相机视场内，未充满相机视场，相机具有一定的运动范围。

因此，本文设计靶标尺寸为200 mm×260 mm，近距离靶面大小为52 mm×65 mm。设计远距离特征点尺寸为40 mm，近距离特征点尺寸为4 mm，远距离靶标工作距离为1.5～100 m，近距离靶标工作距离为0.1～1.5 m。

3.4 合作目标特征点布局

整个靶标可看成远距离和近距离两块不同靶面，靶标背景光源为二极管，保证光强均匀分布在整个靶面。远程靶标和近程靶标为嵌套式独立设计，使用不同的光源，可独立控制。靶标整体布局如图3所示，其中边缘框线为示意靶面大小。靶标尺寸如图3所示。

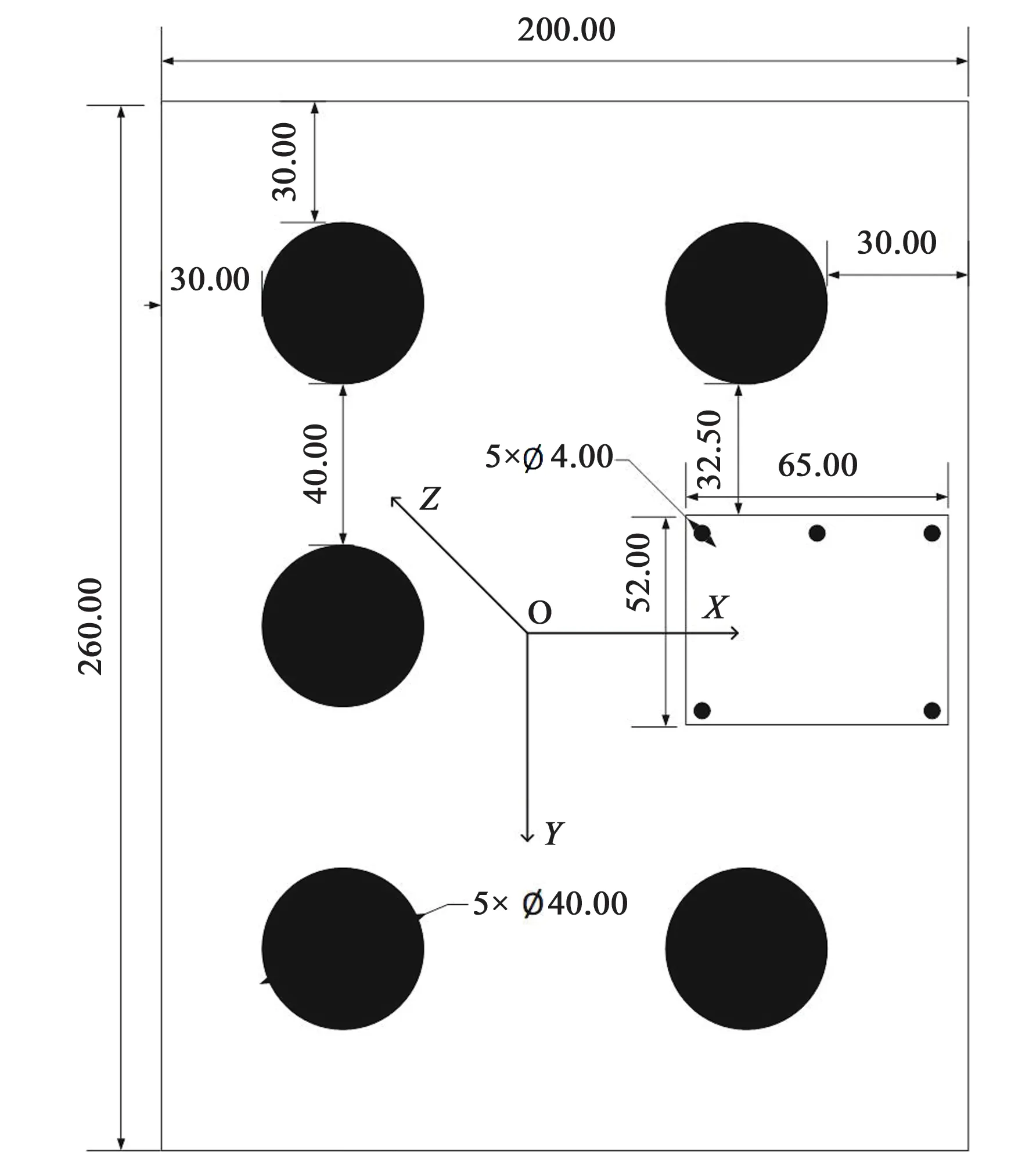
图3 靶标尺寸示意图Fig.3 Schematic diagram of cooperation target size

考虑到白色特征点相对黑色特征点边缘散射更强，在成像时影响特征点图像边缘，不利于后续的图像处理工作，因此所设计靶标背景颜色为白色，特征点颜色为黑色。而宇宙空间为冷黑环境，需要在特征点和靶标边缘有一定的距离来将特征点与环境颜色区分。远距离特征点与靶标边缘距离为30 mm，根据式(4)得出，当物距为100 m，相机焦距为35 mm时，远距离特征点与靶标边缘为2个像素，即在最远处可以将特征点与空间背景成功区分。近距离特征点与近距离靶面边缘距离为2 mm，当物距为1 500 mm，相机焦距12 mm时，近距离特征点与靶面边缘为3个像素，即在两个相机成像最远处可将靶标与背景成功区分。

4 合作目标测量精度分析

位姿解算精度与合作靶标设计、相机镜头畸变、特征点提取精度等因素有关，相机镜头畸变引起的误差可通过相机标定来消除。在不同距离下，由合作靶标引起位置姿态解算误差，对位姿测量精度影响更明显，因此需要对本文所设计合作靶标带来的位置精度和姿态精度进行分析。

4.1 位置测量精度

首先建立合作靶标坐标系，以合作靶标几何中心为原点，建立合作靶标直角坐标系，如图4所示。位置测量精度分析包括XYZ方向的位置精度。图4为Z向位置测量精度原理图。O为相机光心，A、B、C、D、E为靶标特征点。根据成像原理可得Z向位置精度计算公式为：

(5)

式中：∂d为Z向位置精度;∂n为图像质心提取精度，考虑到交会对接时位姿解算的实时性，本文假定特征点质心提取精度为0.5像素;u为传感器像元尺寸;d为物距，为靶标特征点间距;f为相机焦距。根据式(5)得出不同物距下的Z向位置测量精度结果如图5(a)所示。可知当物距最大为100 m时，Z向位置精度为12.61 m；物距最小为100 mm时，Z向精度为0.096 mm。

图4 Z向位置测量原理Fig.4 Principle of position measurement along axis Z

X向位置精度测量原理如图6所示，当特征点A、B移动到A'B'时，可得X向精度计算公式为：

图5 位姿测量误差理论分析曲线图。(a)Z向位置测量精度；(b) X/Y向位置测量精度；(c)Z向姿态测量精度；(d)X/Y向姿态测量精度。Fig.5 Theoretical analysis curve of position and attitude measurement error. (a)Z-direction measurement accuracy; (b) X/Y-direction measurement accuracy;(c) Z-direction attitude measurement accuracy;(d) X/Y-direction attitude measurement accuracy.

(6)

式中：∂l为X向位置精度，∂n为图像质心提取精度，u为传感器像元尺寸，d为物距，f为相机焦距。由式(4)可知，当相机参数一定时，靶标沿X/Y轴方向平移的测量精度只与物距d有关，又因传感器水平方向和竖直方向的像元尺寸大小相等，即Y方向的位置测量精度与X方向相同。根据式(4)得不同物距下X/Y向精度测量结果如图5(b)所示。

图6 X向位置测量精度原理Fig.6 Principle of position measurement along axis X

4.2 姿态测量精度

Z向姿态精度分析示意图如图7所示，特征点AB绕光轴旋转至A′B′，计算公式为：

(7)

式中：为当前物距时相机分辨力大小，∂θ为Z向姿态精度，δn为特征点旋转过的像素。当θ=±(π/2)时，此时Z向姿态误差最大，有δn=l0。代入不同物距得Z向姿态测量精度结果如图5(c)所示。

图7 Z向姿态测量精度原理Fig.7 Principle of attitude measurement along axis Z

X/Y向姿态测量精度示意图如图8所示，当靶标绕X/Y轴旋转时，特征点A、B两点旋转过角度θ至A′、B′,CM为光轴，OC为物距d，AB、A1B1为特征点间距l0，在此基础上可得出：

(8)

nA、nB对θ求偏导可得：

(9)

即：

∂θ=(∂δA·ΔA+∂δBΔB)/2,θ∈[-60°，60°]，

(10)

式中：ΔA、ΔB分别为AB两点的姿态测量精度。

当θ为60°时，姿态测量精度结果如图5(d)所示。

图8 X/Y向姿态测量精度原理图Fig.8 Principle of attitude measurement along axis X/Y

综上所述，在远、近场相机工作的最远、最近距离时，位姿姿态测量精度如表2所示。

表2 不同物距下相对位姿测量精度

由以上分析可知，相对位姿测量精度随靶标与相机之间相对距离减小而增大，距离越近，测量精度越高，如图5所示。当近距离相机单机开始工作时，测量精度越高。另外，当图像不离焦时，靶标成像越清晰，测量精度会有所提升。综上所述，设计的特征点位置和尺寸在最近距离0.1 m处和最远距离100 m处姿态测量误差分别为0.03°和2.89°，满足任务相对姿态指标要求。

5 地面仿真与试验

5.1 合作靶标仿真成像

借助Zemax软件，根据所设计的12 mm和35 mm焦距光学系统在不同物距下对所合作靶标进行模拟成像。其中设置像元大小参数为5.3 μm，传感器像素数为1 280×1 024，与设计保持一致，仿真结果如图9、图10所示。由图可知在物距100 m，使用35 mm相机系统时，特征点所占像素为3×3大小，特征点与合作靶标边缘有2个像素的距离，且每个特征点可被清晰区分。物距为1 m时，特征点与边缘区分清晰，且不充满视场。在物距100 mm时，靶标整体未充满相机视场，特征点易于识别定位，经计算在不同距离下所得仿真图像，合作靶标特征点尺寸大小、特征点与合作靶标边缘距离与理论分析结果一致。

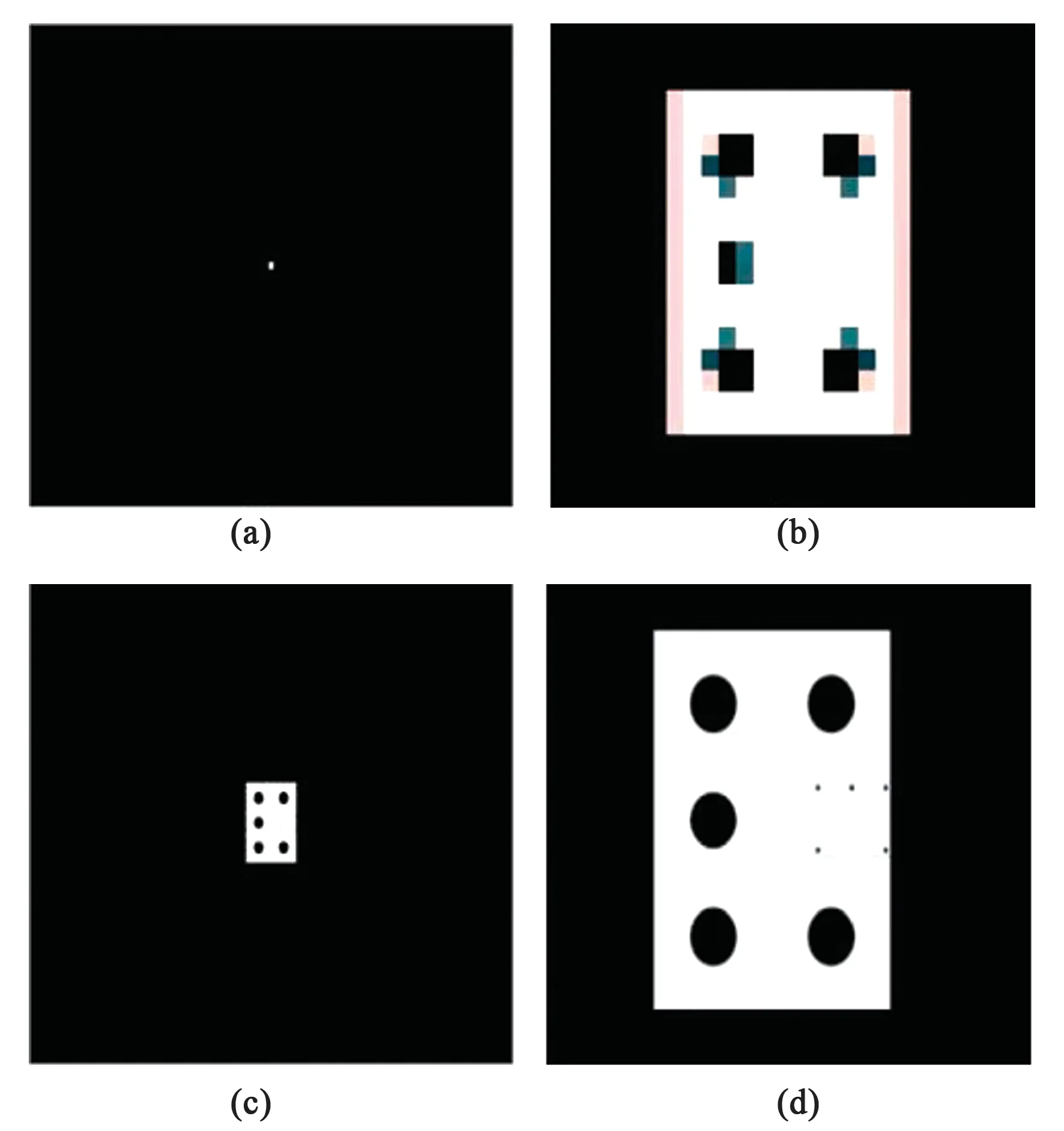
图9 合作靶标35 mm焦距成像系统仿真成像图。(a)100 m成像；(b)100 m成像放大;(c) 10 m成像；(d) 10 m成像放大。Fig.9 Cooperative target 35 mm focal length imaging system simulation imaging diagram. (a) 100 m image；(b) 100 m image magnification；(c) 10 m image；(d) 10 m image magnification.

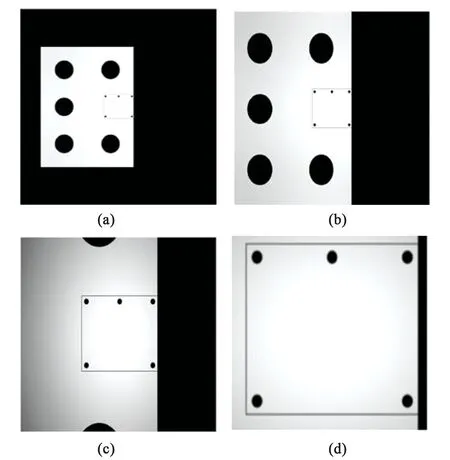
图10 合作靶标12 mm焦距成像系统仿真成像图。(a) 1 m成像；(b) 0.6 m成像；(c) 0.3 m成像；(d) 0.1 m成像。Fig.10 Cooperative target 12 mm focal length imaging system simulation imaging diagram. (a)1 m image；(b) 0.6 m image；(c) 0.3 m image；(d) 0.1 m image.

5.2 合作靶标地面试验

实验选用的相机焦距为25 mm，相机CMOS传感器分辨率为1 280×1 024，像元尺寸为5.3 μm。

图11 合作靶标成像实验。(a)靶标70 m成像；(b) 靶标70 m成像放大；(c)靶标20 m成像；(d) 靶标5 m成像。Fig.11 Target remote imaging test. (a)Cooperative target 70 m imaging；(b) Cooperative target 70 m imaging magnification; (c) Cooperative target 20 m imaging；(d) Cooperative target 5 m imaging.

图12 合作靶标成像实验。(a) 靶标300 mm成像；(b) 靶标500 mm成像；(c)靶标750 mm成像；(d) 靶标1200 mm成像。Fig.12 Target remote imaging test.(a) Cooperative target 300 mm imaging；(b) Cooperative target 500 mm imaging; (c) Cooperative target 750 mm imaging；(d) Cooperative target 1 200 mm imaging.

按文中设计结果制作靶标，模拟在轨交会对接时的无太阳光情况，分别在不同物距下进行成像，测试远距离和近距离的靶标成像情况,如图所示。图11、图12为设计靶标实际测试结果，在物距70 m时，特征点所占像素为3×3像素，代入式(4)中，经计算在不同物距下，实验结果与理论分析一致。

5.3 仿真图像位姿解算精度分析

将仿真图像中X/Y轴位置偏移量和姿态旋转角度皆规定为0°，进行不同物距下的仿真图像位置姿态解算，其中对姿态测量误差进行分析时，将模拟图像选择90°，因为此时Z向姿态误差最大。仿真结果和理论分析结果如图13和表3所示。

理论分析与仿真实验误差来源于质心提取精度误差与成像系统的像差，理论分析时假定特征点质心提取的一般精度为0.5像素。而仿真实验中，特征点质心提取精度随物距变小而增大，因此在远距离时仿真误差大于理论误差，在近距离时仿真误差小于理论误差。除去特征点质心提取精度误差，仿真结果符合理论分析结果，表明合作靶标位置姿态仿真结果与理论分析结果一致。

图13 理论分析与仿真误差曲线。(a) X向位置数据；(b) Y向位置数据；(c) Z向位置数据；(d) X向姿态数据；(e) Y向姿态数据；(f) Z向姿态数据。Fig.13 Theoretical analysis and simulation error curves. (a) X-direction position data; (b) Y-direction position data; (c) Z-direction position data;(d) X-direction attitude data; (e) Y-direction attitude data; (f) Z-direction attitude data.

表3 理论与仿真精度结果Tab.3 Theoretical and simulation accuracy results

6 结 论

针对微小卫星大视距交会对接中，因视觉测量距离变化大，导致合作目标难以被单目相机清晰识别的问题，本文开展合作目标特征点个数、结构布局以及尺寸的设计。该方法克服了由于微小卫星相对距离变化大，导致相机难以获取各阶段高质量合作目标图像，从而不能进行位姿测量的问题。考虑相机焦距和靶标的约束关系，分析并设计合作靶标的特征点尺寸以及位置布局。基于仿真图像分析合作靶标所引起的位姿测量误差，由仿真结果可知，相对物距为0.1 m和100 m时姿态测量误差分别为0.06°和4.01°，验证了所设计靶标的有效性。进一步完成实际成像实验，与仿真理论基本一致，为下一步合作目标识别和定位奠定了良好基础。