基于ST-UKF的高动态GPS载波参数估计*

王小会，李晓青，薛延刚

(兰州工业学院 电气工程学院，兰州 730050)

0 引 言

全球定位系统(Global Positioning System，GPS)是新一代卫星导航定位系统，可以为全球范围内的接收机用户提供全天候的导航信息[1-2]。当卫星和GPS接收机之间具有很高的相对运动时，GPS信号会产生多普勒效应，这将导致采用传统GPS载波跟踪环的普通GPS接收机无法正常工作[2-3]。

对于高动态GPS载波的跟踪，在无法得到多普勒频移时，主要的处理方法是采用多普勒频率估计算法。在20世纪80年代，美国喷气推进实验室(Jet Propulsion Laboratory，JPL)的KUMAR等人[4-6]提出了一系列高动态GPS信号参数估计算法，包括最大似然估计算法、扩展卡尔曼滤波算法、自动频率控制环算法及自适应最小均分算法等[7]。近年来，一些学者也做出了重要的研究：王未未[8]分析了一阶、二阶、三阶锁相环的性能；Zhou等人[9]利用时域差分方程分析了热噪声和动应力对锁相环不同阶次的相位跟踪误差；胡志明[10]采用锁频环辅助锁相环的思想完成了载波跟踪；李静芳等人[11]提出一种基于分数阶傅里叶变换(Fractional Fourier Transform，FRFT)的频率变化率估计方法，利用估计值辅助载波跟踪环路；Wang等人[12]提出了一种基于动态除法快速傅里叶变换(Fast Fourier Transform，FFT)的跟踪算法，以提高GPS接收机的灵敏度；王丽华等人[13]针对传统锁相环(Phase Locked Loop，PLL)环路和卡尔曼滤波环路，分析了其跟踪灵敏度和动态应力性能；Shavrin[14]和Hou[15]对传统跟踪环路中带鉴别器和滤波器的跟踪系统与不带鉴别器的跟踪系统的精度进行了比较分析，分别采用一种卡尔曼滤波估计全球导航卫星系统(Global Navigation Satellite System，GNSS)信号的参数和俄罗斯的格洛纳斯系统(GLONASS)频分多址(Frequency-Division Multiple-Access，FDMA)模型的数据；Liu等人[16]提出一种矢量深组合跟踪环路，采用扩展卡尔曼滤波(Extended Kalman Filter，EKF)对GNSS卫星信号进行跟踪；Zhang等人[17]设计一个双滤波跟踪环路来实现精确的载波跟踪；王睿在分析EKF、无迹卡尔曼滤波(Unscented Kalman Filter，UKF)、中心差分卡尔曼滤波(Central Differential Kalman Filter，CDKF)以及容积卡尔曼滤波(Cubature Kalman Filter，CKF)的基础上，设计了一种带自适应噪声估计器的超紧耦合自适应UKF(Ultra-tight Coupled Adaptation Unscented Kalman Filter，UTC-AUKF)算法[18]。文献[8-10]都是基于传统锁相环或锁频环技术的载波跟踪方案，所采用的都不是基于最优准则设计的相位或频率鉴别器和环路滤波器，限制了环路的性能。文献[11-12]都是利用FFT对GPS载波信号进行傅里叶分析，可能造成一定的误差，从而产生频谱混叠、频谱泄漏以及栅栏效应现象。文献[13-18]都是基于EKF、UKF算法的载波跟踪方案，但是EKF、UKF算法都是应用了线性卡尔曼滤波的递推模式来解决非线性滤波估计问题，存在自身无法克服的理论局限性。

虽然强跟踪滤波器(Strong Tracking Filtering，STF)在系统模型不确定时仍能保持对系统状态的跟踪能力，但是它不可避免要计算雅克比(Jacobian)矩阵并且近似精度只能达到一阶。而无迹变换(Unscented Transformation，UT)和中心差分变换都具有不需要计算Jacobian矩阵等特点[19]，所以本文将强跟踪无迹卡尔曼滤波(ST-UKF)算法应用到高动态GPS载波跟踪环路中，设计基于ST-UKF参数估计器的载波跟踪环路，并分别通过仿真实验与另外四种参数估计器的估计性能进行了对比。

1 基于参数估计器的高动态GPS载波跟踪方案

因传统的GPS载波跟踪环路不能满足高动态环境的要求[20]，故采用非线性滤波算法取代了传统GPS载波跟踪环路结构中的环路滤波器，搭建了如图1所示的基于参数估计器的高动态GPS载波跟踪环路。

图1 基于参数估计器的高动态GPS载波跟踪环路

图1中Zi为数字中频载波信号，该信号经混频和积分清零后得到如下观测信号[2]：

(1)

式中：θ(t)是高动态相位过程，它被定义为

(2)

式中：θ0为初始相位；ω0、ω1和ω2分别为相位各阶导数，分别对应高动态多普勒频移及其一阶、二阶导数。

将输入载波信号和本地复现信号的相位差Δθ及其各阶导数进行泰勒级数展开[2]：

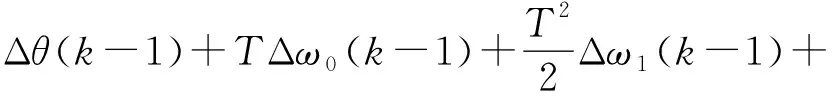
(3)

Δω0(k)=Δω0(k-1)+TΔω1(k-1)+

(4)

Δω1(k)=Δω1(k-1)+TΔω2(k-1)+η3(k),

(5)

Δω2(k)=Δω2(k-1)+η4(k)。

(6)

将式(3)～(6)写成矩阵形式：

(7)

若将系统状态向量记为

x(k)=[Δθ(k) Δω0(k) Δω1(k) Δω2(k)]T，

(8)

过程噪声向量记为

η(k)=[η1(k)η2(k)η3(k)η4(k)]T，

(9)

状态转移矩阵记为

(10)

那么，该动态系统的状态方程可表示为

x(k)=Φk|k-1x(k-1)+η(k)。

(11)

若设向量I=[1 0 0 0]T，并将系统观测噪声记为

(12)

则可将式(1)转化成如下形式：

(13)

得到系统的观测方程。

2 ST-UKF参数估计器的设计

通过在状态预测协方差阵中引入减消因子的方法，强跟踪滤波器能够在线实时调整增益，使得输出残差序列保持相互正交，这样STF在系统模型不确定时仍能保持对系统状态的跟踪能力，但是它依然有理论局限性，不可避免要计算Jacobian矩阵并且近似精度只能达到一阶[19]。而UT变换和中心差分变换对后验均值和协方差的近似精度高于EKF，且不需要计算Jacobian矩阵[19]，故强跟踪无迹卡尔曼滤波将函数Jacobian矩阵的计算用UT变换代替来计算状态的后验均值和协方差，这样既继承了强跟踪滤波器的优点，又无需计算Jacobian矩阵，提高了算法的精度。

由式(11)和式(13)可以推出高动态GPS载波跟踪环路设计的ST-UKF参数估计器的递推步骤如下：

Step1 初始化状态统计特性。

(14)

Step2 选择UT 变换中Sigma点采样策略。

取L=2n，n表示系统状态维数，故Sigma点的数量为2n+1个，则比例修正对称采样Sigma点及其权系数可以表示为

(15)

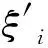
(16)

(17)

λ=α2(n+κ)-n。

(18)

式(17)和(18)中：α是比例缩放因子，取值范围为0≤α≤1；β是权系数，通常取值是β=2；κ是比例系数，通常取值是κ=0。

Step3 时间更新。

γi,k+1|k=Φk|k-1(ξi,k)，i=0,1,…,L；

(19)

(20)

(21)

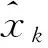
(22)

Step4 量测更新。

(23)

(24)

(25)

(26)

(27)

(28)

(29)

式中：λk+1为减消因子，tr(·)表示求矩阵的迹。

(30)

式中：0<ρ≤1为遗忘因子，通常取ρ=0.95。

于是有

χi,k+1|k=hk+1(ξi,k+1|k)，i=0,1,…,L；

(31)

(32)

(33)

(34)

Step5 滤波更新。

(35)

式中：Kk+1是滤波增益矩阵。

3 仿真分析

仿真软件选用Matlab 7.13。GPS载波跟踪环路的输入信号采用美国喷气推进实验室提出的高动态信号模型[6]。该模型定义接收机动态含有正的和负的加加速度，持续时间为0.5 s，幅度为100g/s(g为重力加速度)，被持续2 s的加速度所分割，仿真时间是8 s[6]。经计算对应的多普勒频率及其各阶导数如图2所示。

(a)多普勒频率

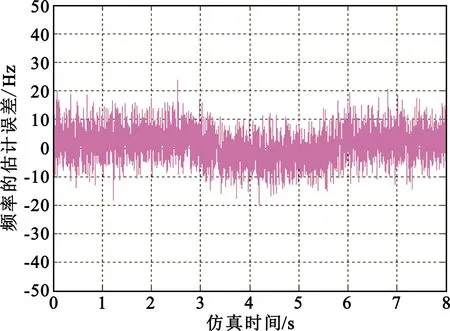
(a)对频率的估计误差

(a)对频率的估计误差

由图3和图4可知，随着环路载噪比的增大，ST-UKF参数估计器的频率估计误差减小。在环路的工作过程中，当加加速度没有发生时，环路的跟踪状态保持稳定，一旦加加速度发生，它会使加速度的方向先由负方向变为正方向，再由正方向变为负方向，频率估计误差的方向也由正方向变为负方向。ST-UKF参数估计器的估计结果证明了本仿真方案的正确性和有效性。

为了对算法进行系统的分析，将ST-UKF算法同基于扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)[20]、中心差分卡尔曼滤波(CDKF)、平方根无迹卡尔曼滤波(Square Root Unscented Kalman Filter，SR-UKF)这四种算法的高动态GPS载波跟踪环路的性能进行了对比，如表1和表2所示。从表1和表2可知，ST-UKF估计器对相位、多普勒频率及其一阶、二阶导数的估计性能呈递减趋势；在高动态正常信号(CNR=30 dB-Hz)条件下，ST-UKF估计器较高动态低载噪比(CNR=20 dB-Hz)条件下对相位、多普勒频率及其一阶、二阶导数进行估计，均方根误差分别减小1.219 2 rad、2.880 5 Hz、8.959 0 Hz/s和17.480 3 Hz/s2；在相同条件下，比如载噪比CNR=30 dB-Hz时，相较UKF估计器，ST-UKF估计器对相位、多普勒频率及其一阶、二阶导数估计的均方根误差分别减小0.157 7 rad、0.593 0 Hz、1.033 0 Hz/s和2.491 7 Hz/s2；无论是弱信号(CNR=20 dB-Hz)还是正常信号(CNR=30 dB-Hz)，ST-UKF参数估计器估计的均方根误差最小，估计精度最高，证明ST-UKF参数估计器的估计性能比其他四个参数估计器性能更优，但其运行时间较长，复杂度较高。

表1 CNR=20 dB-Hz时各参数估计器的均方根误差

表2 CNR=30 dB-Hz时各参数估计器的均方根误差

4 结束语

由于GPS接收机处于典型高动态情况时传统GPS载波跟踪环很难跟踪上信号，为此本文设计了基于ST-UKF参数估计器的高动态GPS载波跟踪环路。实验仿真结果证明了本方案在高动态高载噪比条件下的跟踪结果有了很大的改善。同时，与基于EKF、UKF、CDKF、SR-UKF这四种参数估计器的 GPS载波跟踪环路的性能相比，ST-UKF参数估计器估计的均方根误差更小，估计精度更高，从而验证了本方案的有效性。

虽然ST-UKF参数估计器的估计性能比其他四种参数估计器性能更优，但其复杂度较高，计算量较大，而且以上五种参数估计器都是在设定的高动态环境、高斯噪声的基础上进行的研究，因此不同的高动态环境、非高斯系统都将是以后的研究方向。