三元算术几何平均值不等式的另两种加细
2022-04-26 13:30:30山东省邹平双语学校姜坤崇邮编256200
中学数学教学 2022年2期
山东省邹平双语学校 姜坤崇 (邮编:256200)
安振平老师在文献[1]中给出了三元算术几何平均值不等式的一种加细:
定理设a、b、c>0,求证:
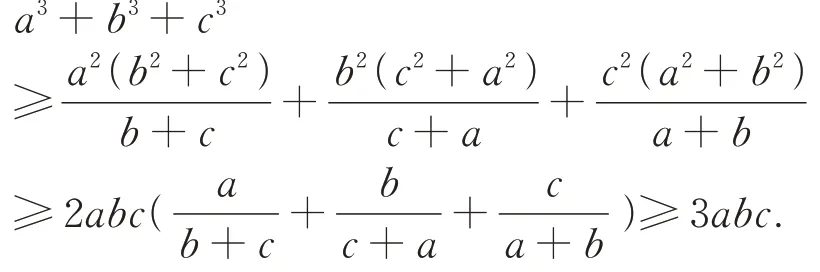
在欣赏以上不等式链之余,受其启发,又发现了三元算术几何平均值不等式的另两种加细,得到以下两个有趣的结论:
命题1设a、b、c>0,则
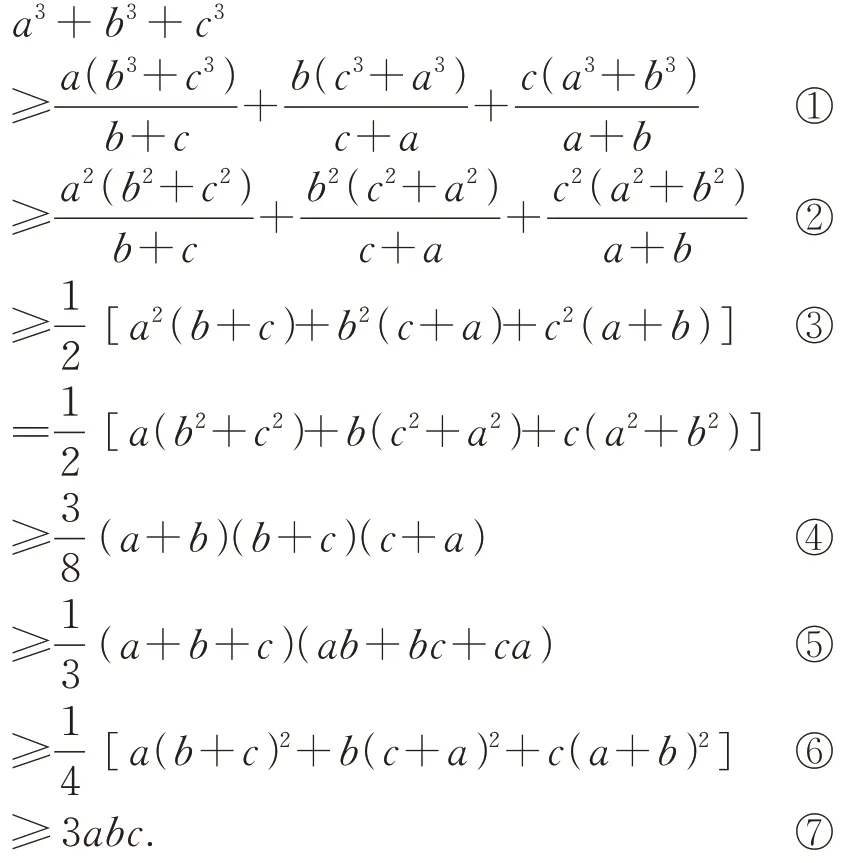
证明需证明以上不等式①~⑦均成立.
先证不等式①,这里,同文献[1]证明文首定理中第一个不等式一样,仍采用作差比较法,得
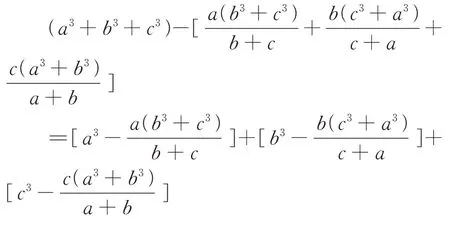
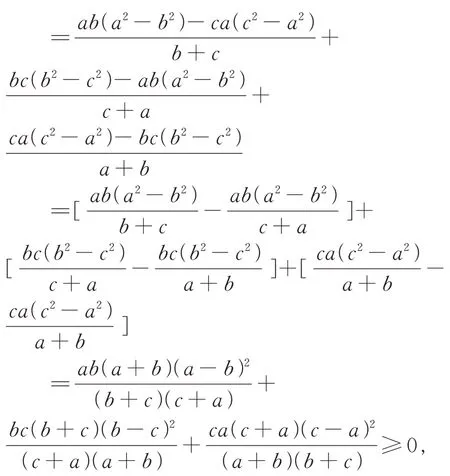
所以不等式①成立.
下证不等式②,还是采用作差比较法,有
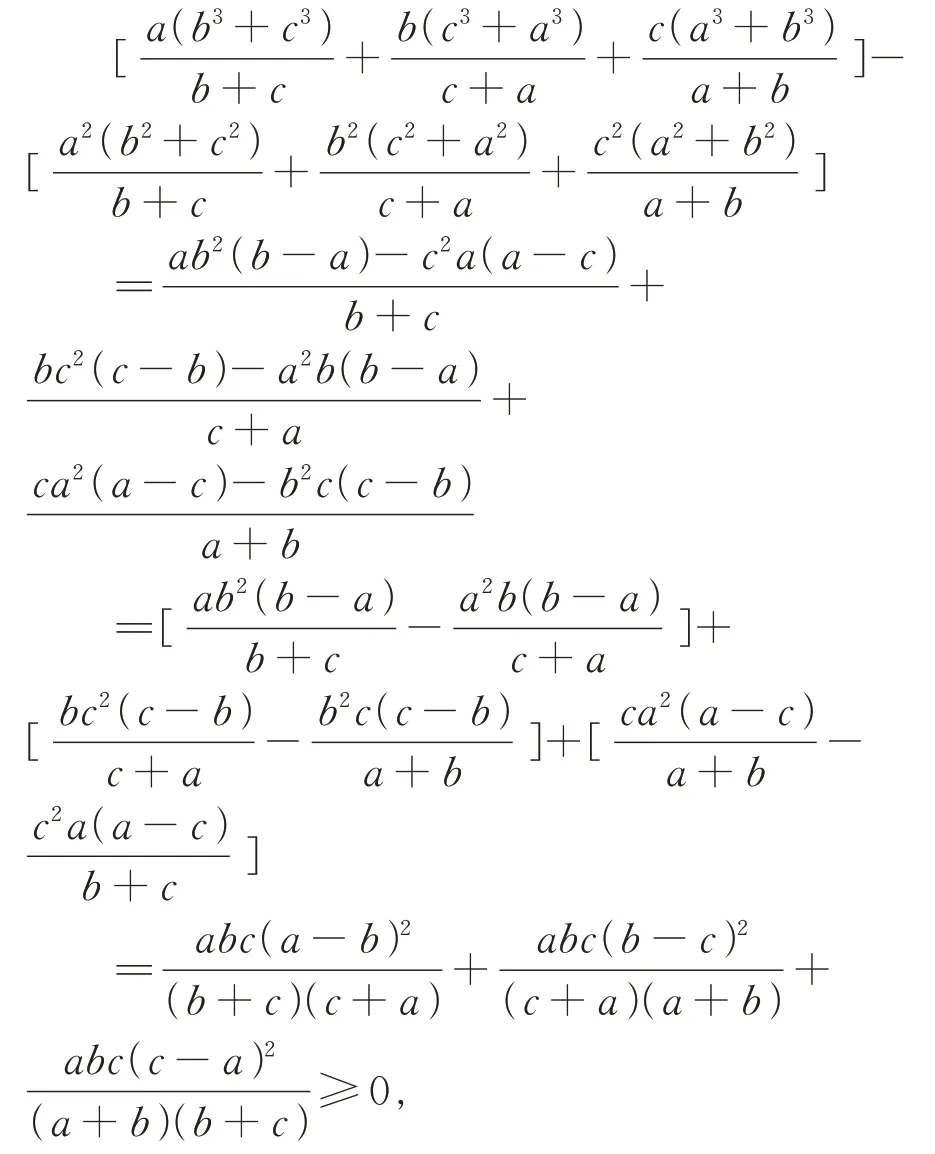
所以不等式②成立.
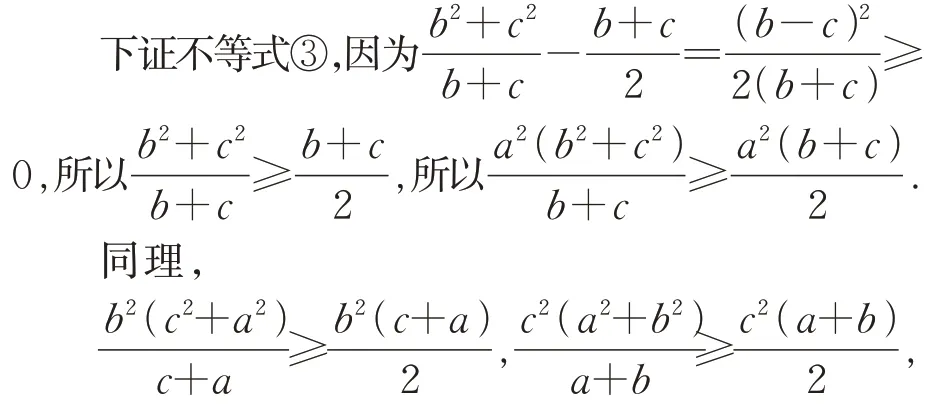
以上三个不等式相加即得③式成立.
容易证明:
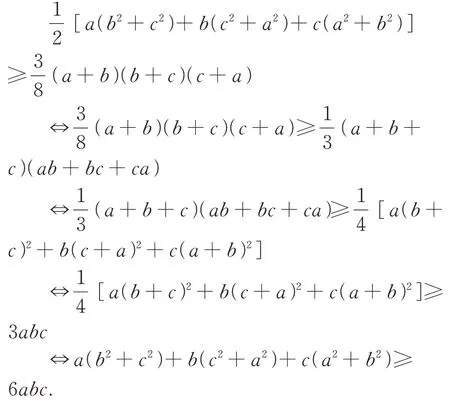
而由二元均值不等式得a(b2+c2)+b(c2+a2)+c(a2+b2)≥2abc+2abc+2abc=6abc,所以⑧式成立,从而④~⑧式成立.
综上,命题1 得证.可以看出,当且仅当a=b=c时,不等式链中的所有不等式的等号成立.
命题2设a、b、c>0,则
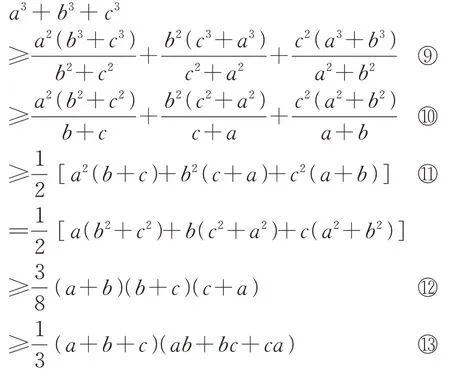
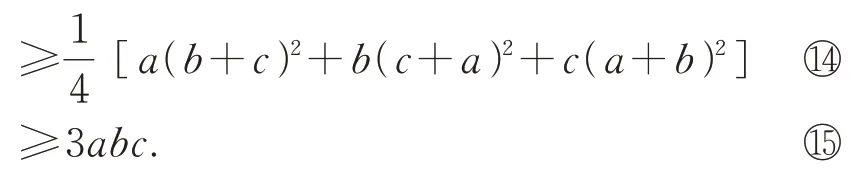
证明先证明不等式⑨,采用作差比较法,得

以下不等式的证明同命题1,从略.
猜你喜欢
初中生世界·七年级(2022年6期)2022-05-28 14:02:01
法律方法(2020年2期)2020-11-16 01:23:00
小天使·二年级语数英综合(2017年9期)2017-10-20 21:09:35
中学生数理化·中考版(2017年11期)2017-04-18 11:14:29
小雪花·小学生快乐作文(2016年12期)2017-03-08 00:50:58
高中数理化(2016年5期)2016-09-26 06:48:04
中学生数理化·高二版(2016年2期)2016-05-30 07:50:39
小天使·一年级语数英综合(2016年5期)2016-05-14 23:32:12
高中生·天天向上(2016年3期)2016-05-05 03:06:38
读写算(中)(2015年12期)2015-11-07 07:25:01

