基于GA-BP算法优化陶瓷加工参数及材料属性*

王抒怀，马廉洁,，闫坤杰，周云光

(1.东北大学机械工程与自动化学院,沈阳 110819;2.东北大学秦皇岛分校控制工程学院,秦皇岛 066004)

0 引言

表面粗糙度和切削温度作为衡量零件质量的重要特性，一直是制造领域的重点研究对象[1-3]，前者直接影响工件使用性能[4]，后者间接影响工件和刀具的使用寿命[5]。工程陶瓷由于具有高硬度、高耐磨、高耐热及优良的化学和电绝缘等特性，近年来被广泛应用于精密仪器、航空航天、医疗机械和国防等中高端制造业领域[6-8]。目前针对工程陶瓷的优化模型一般只针对某种特定陶瓷进行工艺参数优化。诸多研究证明，针对单一实验材料的模型往往不具有普适性。因此将工件材料属性纳入影响因素，并建立基于表面粗糙度和切削温度为优化目标的双目标优化模型，针对不同的陶瓷材料选择最优的工艺参数，对提升陶瓷零件表面质量，延长使用寿命具有重要意义[9-10]。

本文通过车削实验，结合GA算法优化后的BP神经网络，建立了切削温度和表面粗糙度关于工艺参数和材料属性的一元模型和多元模型。结合实际，建立双目标优化模型，通过求解该模型获得一组最优工艺参数和材料属性，并追加实验验证其可靠性。

1 实验

车削材料选择目前应用最广泛的4种工程陶瓷材料：氟金云母、二硅酸锂陶瓷、二硅酸锂玻璃、氧化锆(按照排序顺序对应表中材料Ⅰ～Ⅳ)，工件为直径22 mm圆柱形棒料。刀具选用PCD聚晶金刚石刀具，前角α=-9°，后角γ=19°，刀具圆角半径r=0.05 mm。

分别对上述4种材料进行单因素实验，如表1所示，重复实验3次。将材料作为变量加入正交实验因素水平，如表2所示，进行正交实验，如表3所示,重复实验2次。

表1 单因素实验条件

表2 正交实验因素水平

表3 正交实验条件

车削过程中，使用数字式辐射温度传感器测量工件表面温度。车削结束后，使用Micromeasurez三维表面轮廓仪测量工件加工后表面粗糙度。扫描区域选择3 mm×3 mm，在该区域上随机截取3处1 mm×1 mm测试区域计算其表面粗糙度，取均值作为实验数据。采用FM-ARS9000型全自动显微硬度(纳米压痕)测试系统等设备检测材料属性，如表4所示。

表4 实验工件材料属性

2 遗传算法优化的BP神经网络

BP神经网络是一种多层前反馈神经网络，该网络的主要特点是信号向前传递，误差反向传播。遗传算法是一种并行随机搜索优化方法，以适应度函数作为评判标准的唯一标准，通过选择、交叉、变异操作对个体进行筛选。

本文通过用遗传算法优化神经网络(GA-BP)的初始权值和阈值以达到缩减迭代历程，提升优化效率的目的。将神经网络参数设置为：输入神经元为3，隐含层神经元为5，输出层神经元为1，隐含层函数为logsig函数，输出层函数为purelin函数。遗传算法设置为：种群规模为20，进化次数为500次。算法流程如图1所示。

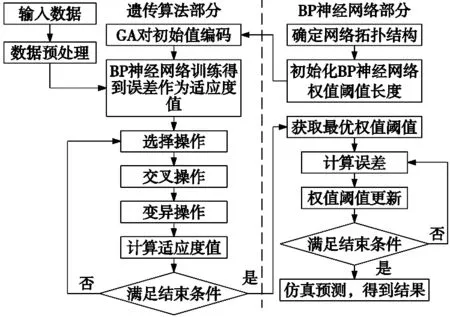
图1 遗传算法优化神经网络流程图

3 基于BP神经网络单因素建模

3.1 工艺参数对切削温度的影响

如图2所示，以切削速度和切削温度的关系为例，首先构建一个BP神经网络模型，并用GA算法对其初始权值和阈值进行优化，将实验中的切削速度及其对应的切削温度分别传递给网络的输入神经元和输出神经元，对神经网络模型进行训练，直至模拟值和真实值的误差小于设定的最大误差(10-6)。利用训练过的神经网络进行预测，以获得足够的数据样本进行拟合。

通过观察实验值和预测值的离散点可以发现切削速度和切削温度整体呈现出明显的线性关系，局部区域有斜率变动。所以提出的一元模型以一元一次函数为基础，乘以指数函数进行修正，加上常量提高拟合度，综上所述，提出切削速度和切削温度的一元模型假设如下：

T(vs)=(avs+b)ecvs+d

通过最小二乘法求解得到模型如式(1)所示：

T(vs)=(-0.011 27vs+1.21)e0.061 72vs+58.6

(1)

式中，T表示切削温度；vs表示切削速度；模型相关系数R=0.989 9,表明模型具有很高的可靠性。

依据上述方法，按照图3、图4所示的变化曲线分别建立切削温度与进给速度(vf) 、切削深度(ap)对应的一元模型，其模型如式(2)、式(3)所示:

(2)

(3)

式(2)、式(3)相关系数R分别为0.966 1、0.992 4。

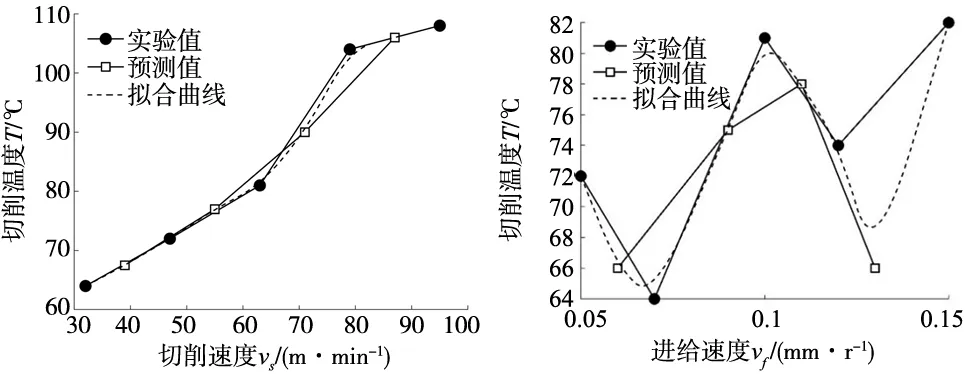
图2 切削速度对切削温度的影响图3 进给速度对切削温度的影响

图4 切削深度对切削温度的影响

3.2 工艺参数对表面粗糙度的影响

同理，参考切削温度的建模方法，建立工艺参数对表面粗糙度一元模型，其拟合曲线如图5～图7所示。经拟合得到的一元模型如式(4)～式(6)所示。

Ra=1.776e0.014 46vs

(4)

(5)

(6)

式(4)～式(6)相关系数R分别为0.978 8、0.990 9、0.968 7。

图5 切削速度对表面 粗糙度的影响 图6 进给速度对表面 粗糙度的影响

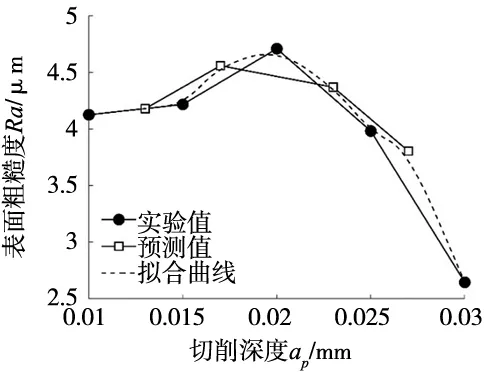
图7 切削深度对表面粗糙度的影响

3.3 材料属性影响切削温度和表面粗糙度

参考表4利用SPSS对不同材料属性进行相关性分析。选择其中影响因子最高的两种材料属性(材料硬度HV和断裂韧性K1c)作为模型变量，并建立与之对应的一元模型如式(7)～式(10)所示，其拟合曲线如图8所示。

Ra=(-0.003 054K1c2+3.061K1c-765.6)×
sin(0.191 1K1c+54.4)+3.89

(7)

T=(0.335 6K1c2-336.5K1c+8.426×104)×
sin(0.126K1c-22.74)+133.8

(8)

T=(-1.77×10-5HV2+0.121 5HV-6.181)×
sin(0.005 16HV-0.851 6)+83.05

(9)

Ra=(-5.473×10-8HV2+3.112×10-4HV+4.44)×
sin(0.149 3HV+0.547 2)+3.687

(10)

式(7)～ 式(10)中的相关系数R分别为0.958 7、0.982 8、0.983 2、0.971 0。

(a) 断裂韧性对表面粗糙度的影响(b) 断裂韧性对切削温度的影响

(c) 硬度对切削温度的影响 (d) 硬度对表面粗糙度的影响

4 多元模型的建立与求解

4.1 多元模型假设

4.1.1 基于切削温度多元模型

基于切削温度关于各工艺参数及材料属性的一元模型式(1)～式(3)、式(8)、式(9)，合并同类函数项，乘以修正系数，建立工程陶瓷切削温度多元模型如式(11)所示：

(11)

式中，m1～m8为常量，具体值由刀具角度及其材料属性共同决定。

4.1.2 基于表面粗糙度多元模型

基于表面粗糙度关于各工艺参数及材料属性的一元模型式(4)～式(6)、式(7)、式(10)，合并同类函数项，乘以修正系数，建立切削工程陶瓷表面粗糙度多元模型如式(12)所示。

(12)

式中，n1～n9为常量，具体值由刀具角度及其材料属性共同决定。

4.2 多元模型求解

基于正交实验中(1～3、5～7、8～11、13～16)组的的结果，利用遗传算法对多元模型中的待定系数进行求解。式(13)为个体适应度函数，等于多元模型的模拟值和正交实验的实验值的最小方差：

(13)

式中，Ai为多元模型模拟值;Ait为实验值。

通过遗传算法对未定参数进行优化求解，获得切削温度和表面粗糙度的多元模型如式(14)、式(15)所示。基于正交实验组(4、8、12、16)对所得模型进行验证，其相对误差如表5所示。

(14)

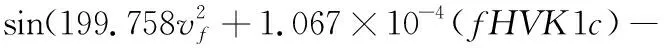
(15)

表5 相对误差 (%)

5 双目标优化模型

在实际加工的过程中，期望维持较低的切削温度，获得更小的表面粗糙度。本文基于切削温度和表面粗糙度多元模型，结合工程陶瓷材料属性和实际加工条件建立如式(16)所示的双目标模型：

F1=min(T(vs,ap,vf,HV,K1c))
F2=min(Ra(vs,ap,vf,HV,K1c))
vs=30～95 m/min
vf=0.05～0.15 mm/r
ap=0.01～0.06 mm
HV=6088～6837
K1c=482～527 J

(16)

基于遗传算法对该模型进行优化求解。以切削温度和表面粗糙度之和的最小值作为适应度评价标准。在正交实验结果中，切削温度和表面粗糙度的变化区间分别为86和3.327。考虑实际需求对二者权重按照3:7分配，得到算法适应度函数如式(17)所示。

(17)

通过算法最终求解得到优化参数如下：vs=32.97 m/min，ap=0.015 mm，vf=0.07 mm/r，HV=6091，K1c=498 J，最小适应度值Fit2=0.465 1，具体迭代过程如图9所示。以上参数带入式(14)和式(15)中，获得对应切削温度和表面粗糙度为：T=22.279°、Ra=0.133 6 μm。

图9 适应度进化过程图

对照表4，4种实验材料中与优化结果中HV和K1c的值最接近的是氟金云母。为验证优化结果，按照优化后的工艺参数对氟金云母展开两组验证实验，并追加两组对照实验：对照实验1将工艺参数重新设置为vs=40 m/min，ap=0.02 mm，vf=0.1 mm/r，不改变工件材料；对照实验2不改变工艺参数，将工件材料改为二硅酸锂陶瓷。实验结果如图10所示。

(a) 验证实验1 (b) 验证实验2

(c) 对照实验1 (d) 对照实验2

可以明显看出，验证实验工件的表面形貌相较于对照实验更规则有序。两次验证实验中的测试结果平均值为T=21.45°，Ra=0.157 3 μm，进一步证明了优化结果的合理性。

6 结论

(1)基于GA-BP神经网络的预测值和单因素实验值，利用最小二乘法，拟合出切削温度和表面粗糙度关于工艺参数及材料属性的一元模型，并通过相关系数证明了模型的可靠性。

(2)整合一元模型得到多元模型，基于正交实验数据，利用GA算法对多元模型中的未定系数进行求解。通过正交实验对模型进行验证，结果表明模型具有较高的精度。

(3)以最小切削温度和表面粗糙度为优化目标，结合实际情况，建立了双目标优化模型。利用GA算法对该模型进行求解，得到了一组最优的工艺参数和材料属性。经过实验验证，该优化结果较为合理。