基于蒙特卡洛的同轴度误差检测测点优化*

黄美发，苟国秋，唐哲敏，梁健伟

(1.桂林电子科技大学机电工程学院，桂林 541004；2.广西制造系统与先进制造技术重点实验室，桂林 541004)

0 引言

同轴度是机械加工零件检测中一种常见的定位公差[1]，对其快速、精确地测量评定具有重要实际意义。三坐标测量机(coordinate measuring machine,CMM)具有测量精度高、测量范围广的优点[2-3]，被广泛应用于机械加工零件几何误差检测。同轴度误差检测时，不仅要保证测量点数足够反映检测零件表面信息，同时也要兼顾检测效率与检测精度。因此，采用CMM进行同轴度误差检测时，制定合理的采样方法和选择合适的测点数尤为重要。

相关国家标准推荐了测点分布方法，比如鸟笼法、圆周线法、母线法及随机布点法，并未给出测量点数的选取方法，对此，QI等[4]使用轮廓信号的奈奎斯特采样定理计算几何误差的测量点数，该方法首先确定截止波长或截止波动数，再确定轴向与径向测点数。然而，该方法计算得到的测量点数偏多，虽然满足测量精度要求，但同时降低了测量效率，增加了测量成本。

近年来，国内外学者针对零件几何误差检测如何选择合适的测点数问题进行了相关研究。对于圆柱面、平面、圆锥面这类规则曲面要素的测量，主要采用Hammersley序列[5]和改进Halton序列[6]这类低差异序列的随机分布方法。对于非规则曲面的测量，主要有粒子群算法[7]、奈奎斯特采样定理[8]、Kriging模型[9]以及Greedy search算法[10]等基于数学过程的方法。现有方法研究了如何在零件测量表面分布测点，使测点分布尽可能的反映零件表面信息，很少考虑零件加工误差来源对测点分布的影响，不同加工方法下加工的零件产生的误差将会影响测点数的分布[11-13]。

针对现有研究的不足，本文将蒙特卡洛法[14]引入到同轴度误差检测测点数的优化中。针对轴类零件同轴度误差检测测点数偏多问题，分析实际加工零件误差来源预测尺寸误差；根据误差来源和同轴度工程语义构建零件表面模拟函数；利用表面模拟函数建立测点模拟函数，通过同轴度误差评定方法分析给定零件测量截面数与误差评定值的关系；进一步基于蒙特卡洛法分析批量零件的最佳测量截面数。最后，通过实例验证该方法的正确性，为工程中零件同轴度检测的测点数选择提供理论指导。

1 零件同轴度误差来源

1.1 零件加工误差分析

实际工程中，零件加工伴随着随机误差，同一批加工出来的两个零件不会完全相同。对于车削加工零件，加工误差主要体现在加工过程中车刀与工件发生相对位置偏移[11]，加工误差大致可以归为两类：一类是已知零件材料、加工刀具、切削用量等确定性条件下产生的确定性误差δC，另一类是由于加工时温度随机变化引起的随机性误差δR。本文分析在相同的装夹方式下，切削力与温度的共同作用导致加工零件形貌发生弯曲变形，从而预测尺寸误差。典型的误差模型包括锥形、凹形、凸形和香蕉形等。

图1给出了车削过程中工艺系统受力变形与尺寸误差的几何关系。基于图1中几何关系，得到加工后零件的实际直径Dw如式(1)所示。

(1)

式中，D表示零件的初始直径;dp表示切削深度;δtx、δty分别表示车刀在X、Y方向的变形量;δmy和δwy、δmx和δwx分别表示在主切削力Fc和背切削力Fp作用下引起工件、夹具变形造成的误差量。通过图1分析得到实际加工零件某z坐标对应的确定性误差δC如式(2)所示。

δC=Dw,z-D+2dp

(2)

零件加工中温度变化引起的随机误差δR如式(3)所示。

δR=ae(ΔTz)(Lz-L)

(3)

式中，ΔTz表示温度的变化量；L为零件加工长度；ae(ΔTz)表示不同温度条件下随机误差曲线斜率，反映随机误差与温度变化关系。最后，得到给定加工条件下零件实际尺寸误差如式(4)所示。

δT=δC+δR

(4)

图1 工艺系统受力变形与尺寸误差的几何关系

1.2 加工零件同轴度几何约束

如图2a所示，加工零件被测轴标注有同轴度公差，且被测轴与基准轴同时应用最大实体要求(maximum material requirement,MMR)；图2b为动态公差图，表示被测轴轴线应在公差带内。相关标准对图2标注零件具有以下要求：

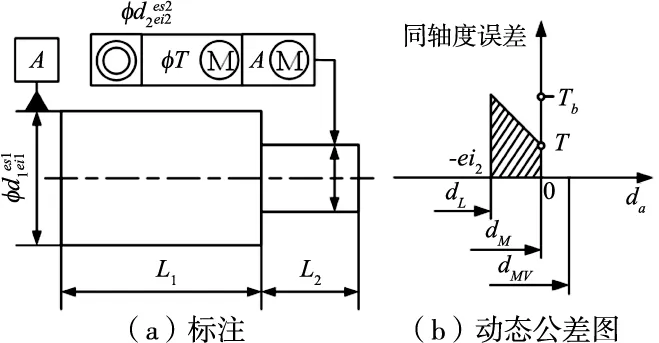
图2 同轴度公差与动态公差图

(1)被测轴与基准轴的局部尺寸da处于各自最大实体尺寸(maximum material size，MMS)和最小实体尺寸(least material size，LMS)之间，即dL≤da≤dM，dL等于公称直径d加上偏差es，dM等于公称直径d加下偏差ei。

(2)被测轴与基准轴的体外作用尺寸dfe不得超过各自最大实体实效边界(maximum material virtual boundary,MMVB)，且两者的MMVB同轴，即dfe≤dMV，dMV等于MMS加上同轴度公差值，dfe表示与实际孔体外接触的最大理想表面直径。

(3)当da=dM，对应的同轴度公差为T，当da=dL，尺寸误差补偿同轴度公差，此时对应的同轴度公差为Tb，Tb=es2-ei2+T。

2 零件表面形貌模拟

2.1 加工零件表面模拟函数

通过第一节中预测加工零件尺寸误差，模拟出标注有同轴度误差的零件表面形状，以图2检测零件为例，当满足1.2节中同轴度误差要求，误差允许值变大，模拟测点区域变宽。设已模拟零件表面一系列测点，绘出图3所示测点误差分布曲线图，可计算零件表面第i个测点实际直径Dp,i，如式(5)所示。

(5)

式中，d为零件公称直径；xi(i=1,2,...,I)为0～1内的随机变量，xi集合服从正态分布：xi～N(T/2,σ)，表示随机变量xi的均值；Dp,i表示零件上第i个测点的实际直径。

图3 测点误差分布曲线图

当一次测量随机变量xi达到下极限xi,m时，实际直径达到极小值Di,m，式(5)变为式(6)：

(6)

同理，随机变量xi达到上极限xi,M时，实际直径达到极大值Di,M，式(5)变为式(7)：

(7)

当|δ|=3σ时，一次测量不超出|δ|的概率为99.73%，由于|Tb|=6σ，可得到圆柱径向截面某测点的实际直径如式(8)所示，从而得到具有如图1所示标注信息的零件表面形状模拟函数。

(8)

式中，Tb为尺寸误差δT补偿同轴度公差后所允许的同轴度公差，如图2b所示，即Tb=δT+T。

2.2 零件表面测点模拟

本文采用周向均匀布点，径向方向非均匀布点方法，每个截面测点数N由经验公式得出，如式(9)所示。

(9)

式中，ε=(1/3～1/10)T为测量允差；ε2为三坐标测量机误差；R为圆柱体公称半径；θ为测点间角度。

如图4b所示，模拟表面误差在X、Y、Z方向分别由三个尺度的轴向误差与径向误差合成。根据2.1节给定零件的模拟函数，模拟零件截面上所有测点{qi,n=(xi,n,yi,n,zi,n)T；n=1,2,...,N(N>3)；i=1,2,...,I}作为零件表面提取要素。测点精度模拟函数如式(10)所示。

(10)

式中，i为截面序号；n为每个截面上的测点序号；R是被测轴段半径；t1是测量截面位置的不确定度；L是被测轴段长度；Zi,j分别表示截面i在z坐标方向上的误差尺度的随机误差系数，服从正态分布N(0,1)；j(j=1,2,3)表示三个误差尺度的幅值和频率系数。

图4 公差标注与模拟测点示意图

3 同轴度误差检测测点优化

3.1 测量截面数与误差评定值的关系

根据同轴度误差评定准则，调用评定算法对2.2节中得到的测点集{qi}进行误差评定，分析零件测量截面数与同轴度误差评定值的关系，如图5所示。

图5 截面数与误差评定值的关系

每个圆周截面均匀分布相同数量测点，随着截面数增加，零件同轴度误差增加，但当截面数增加到一定数目，零件误差值基本趋于稳定。继续增加测量截面会影响测量效率和增大测量成本，所以，满足零件精度要求时的测量截面数可作为最佳测量截面数。

3.2 测量截面数优化

本文引入蒙特卡洛法仿真原理思想，将被测零件测量长度L、圆周截面测点数目N、同轴度公差T、测量允差ε以及初始截面数Ic作为算法输入，输出最佳截面数I，最后得到最佳测量点集，其步骤如下所示：

步骤1：输入L、N、T、ε及Ic，其中(N≥3)；

步骤2：逐渐增加测量截面数；

步骤3：根据式(9)得到符合正态分布的测点集(j=1,2,…,M)；

步骤4：计算零件体外作用尺寸，模拟M组测点集(M≥20)，计算M组测点集体外作用尺寸平均值的变化量Δ；

步骤5：根据测点模拟基于“误差评定的结果服从正态分布”这一假设，设置判定条件：Δ≤0.001，模拟测点符合所要求样本条件，且同轴度误差服从正态分布，执行下一步；否则返回步骤3，直到符合条件；

步骤6：计算体外作用尺寸平均值与其测量指标的差值，即测量误差。当测量误差不超过测量允差时，停止增加截面数；否则返回步骤2继续增加截面数，循环迭代直到符合判断条件，最后输出测点集。

4 实例验证

4.1 实例测点数生成

如图6所示为某标有同轴度公差的实际阀芯，通过MATLAB R2018a软件模拟零件表面测点并进行测量结果不确定性分析，用于验证方法的正确性，最后再用三坐标测量机进行测量，用于验证方法的可行性。

图6 某阀芯尺寸与几何公差规范

本文研究悬臂装夹方式下加工的零件，在切削力与温度作用下，其尺寸误差与加工尺寸的关系如图7所示，其误差模型为香蕉形，加工最大尺寸误差为0.071 3 mm，符合尺寸误差要求。

图7 尺寸误差与加工长度关系图

尺寸误差补偿同轴度公差，得到综合公差Tb=0.1+δT。阀芯为阶梯轴，进行同轴度误差检测需测量基准轴与被测轴两个圆柱体，将各自轴段长度L，测量允差ε=0.01～0.066 7 mm，取ε=0.066 7 mm，三坐标测量机误差ε1=0.003 mm，带入式(8)计算得到被测轴与基准轴单个截面上测点数分别为N1=41、N2=42，输入相关参数到3.2节步骤，计算出被测轴的体外作用尺寸的平均值以及测量误差，部分结果如表1所示。

表1 被测轴体外作用尺寸平均值及测量误差

对比表1中数据，截面数越多，被测轴体外作用尺寸平均值越大，当截面数达到一定数量时，测量误差变化量逐渐减小。

如表1所示，被测轴截面数为10时，体外作用尺寸平均值为34.833 8 mm和34.833 9 mm，此时对应的测量偏差为0.066 1 mm，满足小于等于测量允差(ε)的判定条件，虽然继续增加截面数测量误差继续变小，但每增加一个截面会增加41个测点，从而减小测量效率，增加测量成本，所以被测圆柱体建议采用10个截面，每个截面41个测点进行测量。

同理，基准轴测量部分结果如表2所示，可以看出，基准轴建议采用12个截面，每个截面42个测点进行测量，轴测图实例模拟如图8所示。

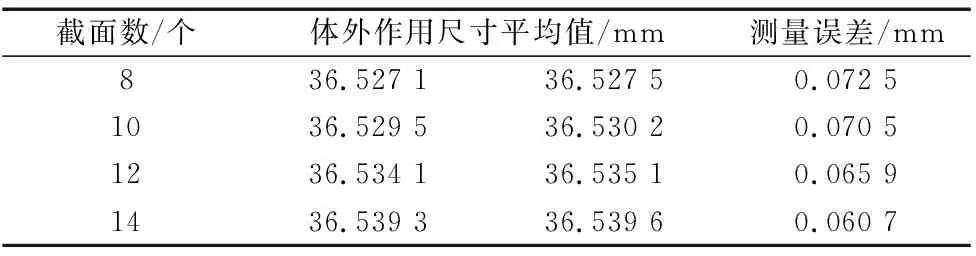
表2 基准轴体外作用尺寸平均值及测量误差

图8 零件表面模拟示意图

采用文献[4]的方法对该零件进行测点数计算，其轴向测点数，即测量截面个数如式(11)所示。

I=2a≥7L/λec

(11)

径向测点数，即每个截面测点个数如式(12)所示。

N=2b≥7πd/λec

(12)

其测点结果与本文测量结果对比如表3所示。

表3 不同测点数选取方法对比

通过表3对比，本文所提出的测点优化方法能够有效提高测量效率，降低测量成本。

4.2 测量结果不确定度分析

截面数将会影响三坐标测量机评定同轴度公差时的评定结果不确定度，同时给测点模拟和评定过程带来不确定度，通过分析该实例不同测点数下的测量结果不确定度，以验证所提出模拟方法的准确性，如图9所示。

图9 测量结果不确定度评定流程

根据蒙特卡洛法分析测量结果不确定度，将被测圆柱体推荐截面数I=10，单个截面测点数N=41带入评定流程，分析多组测点时被测圆柱体的体外作用尺寸包含区间，从而判定零件合格性。

国标规定，要计算包含概率为95%的包含区间，需要模拟计算10 000次[14]，其体外作用尺寸包含区间如图10所示。其包含概率为95%的包含区间为[34.826 5,34.844 8] mm，总耗时351 s，平均耗时0.035 1 s，测点模拟算法鲁棒性较好。

图10 体外作用尺寸

4.3 实例的CMM验证

针对4.1节中的实例采用CMM进行验证，如图11所示。

图11 CMM实例测量

使用三坐标测量机为Hexagon Metrology生产的GLOBAL CLASSIC SR 07.10.07，测量精度为0.003 mm，基准轴和被测轴单个截面分别测量41、42个点，截面数分别为10、30进行测量，其被测轴测量评定结果如表4所示。

表4 阀芯评定结果

分析表4可得，当被测轴采用10、30个截面进行零件测量，评定都符合要求，零件都合格，两者评定结果仅仅相差0.003 1 mm，但采用30个截面却多增加了820个测点数，降低了测量效率，增加了测量成本，所以实际测量中，该实例建议采用10个测量截面即可满足精度要求。

5 结论

本文重点研究了数字化测量环境下同轴度误差检测的测点优化问题。分析零件的误差来源，预测零件尺寸误差；根据误差理论规定随机测量的概率范围构建测点集模拟函数，模拟零件表面；分析测量截面数与误差评定值之间的关系，基于蒙特卡洛法优化测点数。

通过某阀芯实例验证该方法正确性与有效性。与现有理论方法相比，所提方法在满足精度要求下，轴向、径向测点数分别减少983、246个，为解决目前同轴度误差检测测点数偏多问题提供新方法。

本文仅考虑了单一加工方式下零件误差来源对零件同轴度误差测量的影响，未来可研究不同加工方式下几何误差的智能化测量。