改进状态方程的电动静液作动器稳定位置跟踪*

朱新波，刘亮龙，唐海涛

(1.广西师范大学漓江学院理工学院，桂林 541006；2.桂林航天工业学院理学院，桂林 541004)

0 引言

由于具有宽输出功率范围和紧凑的驱动系统等优点，液压作动器十分适合用于机器人系统。大多数液压作动器都是由伺服阀驱动的，因为伺服阀具有良好的控制性能。然而，使用伺服阀的液压系统有几个缺点，例如动力效率很低、系统体积大、伺服阀价格昂贵等问题[1-4]。

目前，研究人员已开始使用EHA来尝试解决上述问题[5-6]。然而，由于伺服电机和泵的转动惯量的原因，EHA具有较差的控制性能。因此，OBOE等[7]提出使用负载侧传感器来抑制谐振的控制方法，其常规控制器的状态方程用驱动侧位置/速度和负载侧位置/速度描述。虽然上述谐振抑制技术可以有效地改善EHA的性能，但由于EHA存在内部漏油现象[8-9]，导致其具体实施时存在稳定性较差的问题。这是因为漏油引起的角度漂移引起EHA的参数产生一定扰动。综上所述，当同时补偿电机侧和负载侧位置时，反馈系统会受到无界扰动，即漏油引起的角度漂移而产生失稳现象。

为解决这一问题，本文提出了一种新的基于负载侧位置/速度/加速度和相对速度的状态方程。由于该方法不需要电机侧位置，可以排除角度漂移，即使在漏油的情况下也能获得稳定的位置跟踪。然后，在此基础上，提出了一种针对EHA的全状态控制器。通过带机械臂的液压系统实验，验证了该方法的可行性和有效性。

1 EHA系统建模

EHA的工作示意图如图1所示。

图1 EHA的工作示意图

在本研究中，如图1中所示的伺服泵被称为电机侧，液压马达被称为负载侧，则负载侧的动力学方程[10]如下：

(1)

(2)

(3)

带有下标1的变量表示负载侧的变量，下标为m的变量代表电机侧的变量。电机侧的动力学方程如下：

(4)

式中，u为伺服电机产生的基准扭矩；Dm为电机侧排量。

由于存在漏油，电机侧产生的部分油流量会减少，例如：

(5)

(6)

这是一个简化的漏油模型，它实际上具有非线性特性：在高速区域泄漏量很小，而在低速区域泄漏量急剧增加，液压系统中存在较大的静摩擦。因此，EHA有两个死区:漏油和静摩擦，EHA的原理框图如图2所示。

图2 EHA的原理框图

文献[11]采用了反馈调制器来克服死区问题。因此，本文也使用反馈调制器对静摩擦引起的死区进行了补偿，以便抑制静摩擦的影响，同时提供足够高的速度来避免漏油，则图4可以线性化，因为省略了两个死区。因此，无死区的EHA动力学可以建模如下：

(7)

(8)

2 带有相对速度的状态方程设计

(9)

(10)

式中，θleak为漏油引起的角度偏移；Jm为电机侧惯量。

本例患者的临床表现、心电图特征以及病情进展都符合de Winter综合征的表现，在临床工作中及时发现并深刻认识这种特殊的心电现象，对挽救患者生命具有重要意义。该心电图表现易被误诊为前壁心肌缺血，从而导致再灌注时间明显延迟。因此，临床医生或心电图工作者如果发现有此种心电图特征，建议立即行急诊冠脉造影及再灌注治疗。

角度偏移θleak的实际值是无法测量的，而该时变角偏移量使EHA不稳定，全状态反馈控制器不能在EHA得到正常实现。

为解决这一问题，提出了一种利用相对速度的状态方程。通过定义相对位置θr=θm-nθ1-θleak，从式(9)和式(10)导出相对位置的动力学方程如下：

(11)

(12)

(13)

(14)

由式(11)和式(13)可得：

(15)

最后，由式(14)和式(15)推导出使用相对速度的状态方程。

(16)

θ1=cx

(17)

(18)

(19)

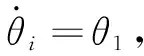
3 全状态反馈控制

目前，工业上广泛应用的控制器为比例-积分-微分(proportional derivative integral,PID)控制器[14]和比例-比例-积分(proportional proportional integral,PPI)控制器[15]。

PID控制器的控制输入如下:

(20)

PPI控制器的控制输入如下:

(21)

不同于上述两种控制器，该系统可以通过全状态反馈控制器[13]-fx来实现稳定，并通过前馈控制器Cff来改善跟踪性能。这里，f=[KiKpKvKaKr]。然后，u=-fx+Cffθcmd代入式(16)。

(22)

式中，θcmd为指令值。

指令与响应之间的关系如下：

θl=c(sI-A+bf)-1bCffθcmd

(23)

全状态反馈控制系统过程中所涉及的5个参数的定义如下：

(24)

(25)

(26)

(27)

Kr=5Jm

(28)

Cff的计算方式如下：

(29)

从上述公式可以看出，全状态反馈控制的主要目的是将控制输入u=-fx+Cffθcmd进行量化并超过最大静摩擦，并且量化误差的影响通过使用反馈调制器来抑制，也就是说，通过使用反馈调制器来抑制量化误差的影响，从而克服了漏油引起的角度漂移而产生失稳现象。所提方法的整体框图如图3所示。

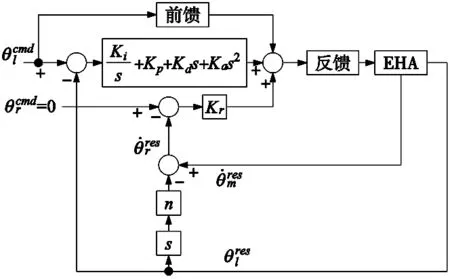
图3 所提方法的整体框图

4 实验结果与分析

4.1 实验设置

图4 实验所用液压系统

图4所示系统中电动伺服电机型号为Maxon E-60，液压马达型号为Eaton S-380 ，两者的位置响应均由17 bit分辨率的光学编码器测量得到。液压泵的型号为Eaton MA-03。液压马达与机械臂连接，机械臂如图5所示。

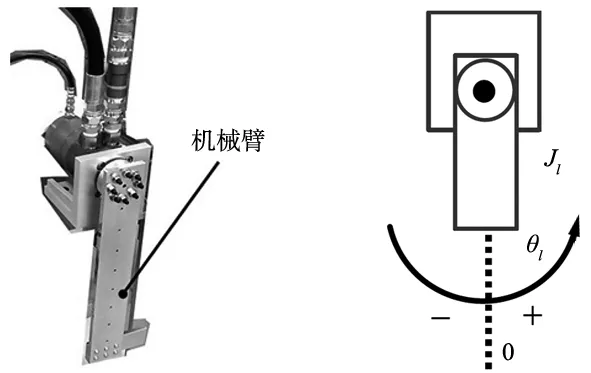
(a) 实物图 (b) 模型

实验参数如表1所示。

表1 实验参数

4.2 结果分析

使用正弦波和阶跃指令的实验结果分别如图6和图7所示。

(a) PID控制(10 rad/s) (b) P-PI控制(10 rad/s)

(c) 所提方法(10 rad/s)图6 0.3 Hz正弦波的实验结果

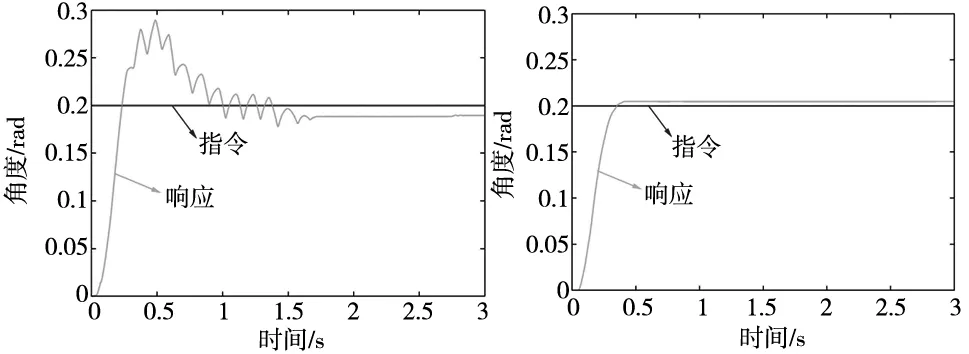
(a) PID控制(10 rad/s) (b) P-PI控制(10 rad/s)

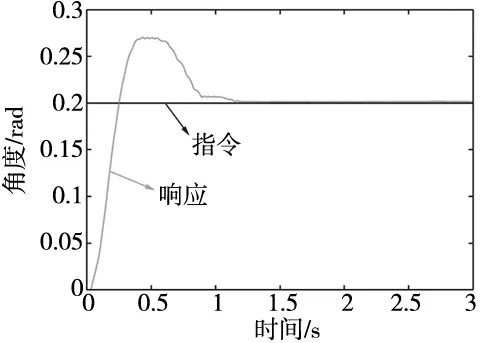
(c) 所提方法(10 rad/s)图7 阶跃指令的实验结果

从图6a可以看出，PID控制器中观察到较大的相位滞后。图7a显示了漏油引起的较大稳态误差。在P-PI控制器的情况下，虽然获得了如图6b所示的稳定响应，因为P-PI控制器利用了电机和负载侧信息。但是，P-PI控制器不能恢复相位滞后。此外，P-PI控制器不能完全补偿稳态误差，如图7b所示，因为负载侧指令和响应之间没有积分控制。

不同于PID控制器和P-PI控制器，所提方法在抑制相位滞后的同时，也抑制了稳态误差，如图6c和图7c所示，因为所提出的方法是全状态反馈控制器，并且从状态方程中排除了漏油的影响，获得了最佳的稳定位置跟踪性能。

5 结束语

本文提出了一种新的EHA状态方程，以获得控制性能更好的全状态反馈控制器。为了排除漏油引起的角度漂移的影响，选择相对速度和负载侧位置、速度、加速度作为状态变量。并通过所提出的状态方程设计了相应的全状态反馈控制器。实验结果表明，所提方法获得了具有高反馈增益的稳定位置跟踪效果，有效解决了漏油对EHA全状态反馈控制器的不良影响。后续将对所提方法的鲁棒性开展进一步验证分析。