用于城轨直流牵引系统的混合型MMC全桥子模块比例设计方法

席嫣娜，李笑彤，李子明，魏应冬，李笑倩，王方敏，李伟，李伟瑞

(1. 国网北京市电力公司，北京 100031；2. 电力系统及发电设备控制和仿真国家重点实验室（清华大学电机系），北京 100084；3. 北京电力经济技术研究院有限公司，北京市 100055)

0 引言

目前中国地铁多采用1 500 V或750 V的直流牵引供电方式[1]，牵引变电所基本上都采用二极管不控整流装置[2-3]，直流电压不可控且能量只能单向流动。当列车运行在制动模式时，列车的电机进入到发电工况，制动能量无法回馈给交流电网，还会导致牵引网直流电压显著升高，必须通过列车内部的制动电阻进行消耗，造成较大的能源浪费。

当二极管不控整流装置被替换为电压源型双向变流器后，每个牵引所的节点电压就可以根据系统级的策略进行控制。通过判别机车当前处于牵引状态还是制动状态，灵活地调节全线各节点的电压，实现直流线路上的潮流可控、调度优化。运用电力电子技术的双向变流器有着直流电压稳定可调、能量双向流动、功率解耦控制等特性[4-5]。目前用于低压直流系统的双向变流器基本上都使用两电平的三相半桥拓扑，其峰值功率不足，难以满足实际情况的需要。为提升峰值功率并联多重化时会带来动态均流和稳态均流的问题[6-7]。模块化多电平换流器(modular multilevel converter, MMC)是高压柔性直流输电领域应用最广泛的双向变流器拓扑[8-9]。相比于常规的两电平变流器，MMC有着谐波含量小、容量上限高、模块化设计方便拓展等优势[10-11]。

城市轨道交通直流牵引供电系统是一个低电压大电流的系统，交流电压等级较高而直流电压等级较低，适合选用混合型MMC拓扑[12-14]。混合型MMC的桥臂由全桥子模块和半桥子模块混合构成，有较高的电压调制比。全桥子模块输出负电平，可以降低桥臂的交流电流[15]，减少开关器件中的峰值电流。在选择同样电流等级的开关器件时，混合型MMC的峰值功率明显大于现有的两电平变流器，还具有直流故障清除能力[16-18]，可以隔离牵引网和公共电网，减少直流断路器的使用。

混合型MMC的全桥子模块比例是主回路参数中最基础的参数[19]，直接影响着拓扑方案的经济性。目前混合型MMC的全桥子模块比例设计方法基本上都是在调制比小于1的工况下[20-21]，在调制比大于1的工况下全桥子模块比例的设计方法研究比较少。文献[22-23]对混合型MMC稳态运行时桥臂电压输出范围和全桥子模块比例的关系进行了说明，主要应用在中高压输电领域。文献[24]研究在调制比小于1的工况下使用闭锁控制方式清除直流故障，全桥子模块的配置比例需要满足的条件。文献[25]研究在调制比大于1的工况下使用零直流电压控制清除直流故障，全桥子模块的配置比例需要满足的条件。在直流牵引系统中，没有对换流站快速重启的需求，而是要求线路上相邻换流站具备运行能力来保证供电持续性，所以在调制比大于1时，可以使用可靠性和经济性更好的闭锁方式清除直流故障。在低压大电流系统中设计MMC参数，电容电压波动是次要因素，而桥臂电流峰值是主要的影响因素。本文针对城市轨道交通直流牵引供电系统的特点，提出一种混合型MMC全桥子模块比例的设计方法，适用于MMC长期运行在调制比大于1的工况下。在设计参数时直接将牵引直流电压和全桥子模块数量关联起来，稳态运行时MMC的输出能力需求自然满足，暂态故障时用闭锁方式清除直流故障。

1 混合型MMC拓扑

混合型MMC的直流牵引供电系统如图1所示，MMC主回路及子模块拓扑如图2所示。一个单元由上、下两个桥臂组成，每个桥臂由N个子模块和一个桥臂电感串联而成，N个子模块包含F个全桥子模块和H个半桥子模块，满足N=F+H。全桥子模块由绝缘栅双极型晶体管（IGBT）全桥和储能电容组成。半桥子模块由IGBT半桥和储能电容组成。

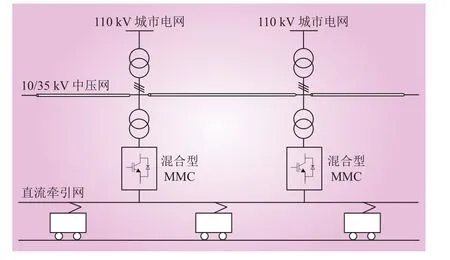
图1 使用混合型MMC的直流牵引供电系统Fig. 1 DC traction power supply system based on hybrid MMC

图2 混合型MMC拓扑Fig. 2 Hybrid MMC topology

混合一般指全桥子模块和半桥子模块混合，通常可分为2种混合方式：同一个桥臂内不同子模块混合，上桥臂和下桥臂的全桥子模块比例相同；桥臂间不同子模块混合，全桥子模块全部集中在某一个桥臂。考虑到上下桥臂电压的对称性，以及为了能够灵活设计全桥子模块的比例，本文研究的混合型MMC为同一个桥臂内不同子模块的混合方式。

2 全桥子模块比例设计原理

设变流器的容量为S，直流电压为Udc，直流电流为Idc，交流相电流峰值为Im，交流侧功率因数为cosφ。则电压调制比m为

式中：Um为交流相电压峰值。

以a相为例，上下桥臂电流为

式中：iap为a相上桥臂电流；ian为a相下桥臂电流；ω为角频率；φ为功率因数角；t为时间。

混合型MMC输出的直流电压等于牵引电压750 V或1 500 V，交流端经过三相变压器和10 kV或35 kV系统相连。在满载时，MMC中的直流电流很大，桥臂中的直流分量占据了桥臂电流容量的很大一部分。为了降低桥臂电流容量，需要降低MMC桥臂中的交流电流，那么可以提高MMC的交流电压，使得调制比m＞1，全桥子模块长期处于负电平输出状态。

2.1 稳态运行的需求

交流电压和直流电压波形如图3所示。当交流侧电压达到正向峰值时，上桥臂需要输出最大的负电压，下桥臂需要输出最大的正电压。

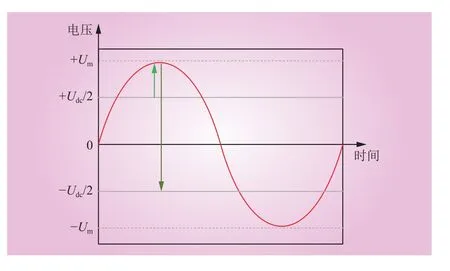
图3 交流电压和直流电压波形Fig. 3 AC voltage and DC voltage waveform

桥臂子模块数目和全桥子模块数目需要满足稳态运行时的输出能力，即

式中：Uc为子模块电容电压。

若Udc为Uc的整数倍K，则式(3)可简化为

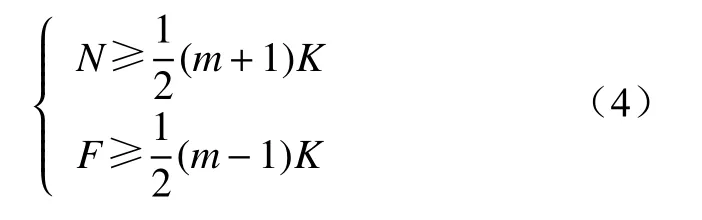
2.2 直流故障清除能力的需求

当系统的直流侧发生线间短路故障时，混合型MMC快速闭锁所有子模块，子模块电容串联在交流回路中，产生反电动势，使得所有二极管截至，从而阻断直流侧的故障电流[26]，直流故障电流通路如图4所示。

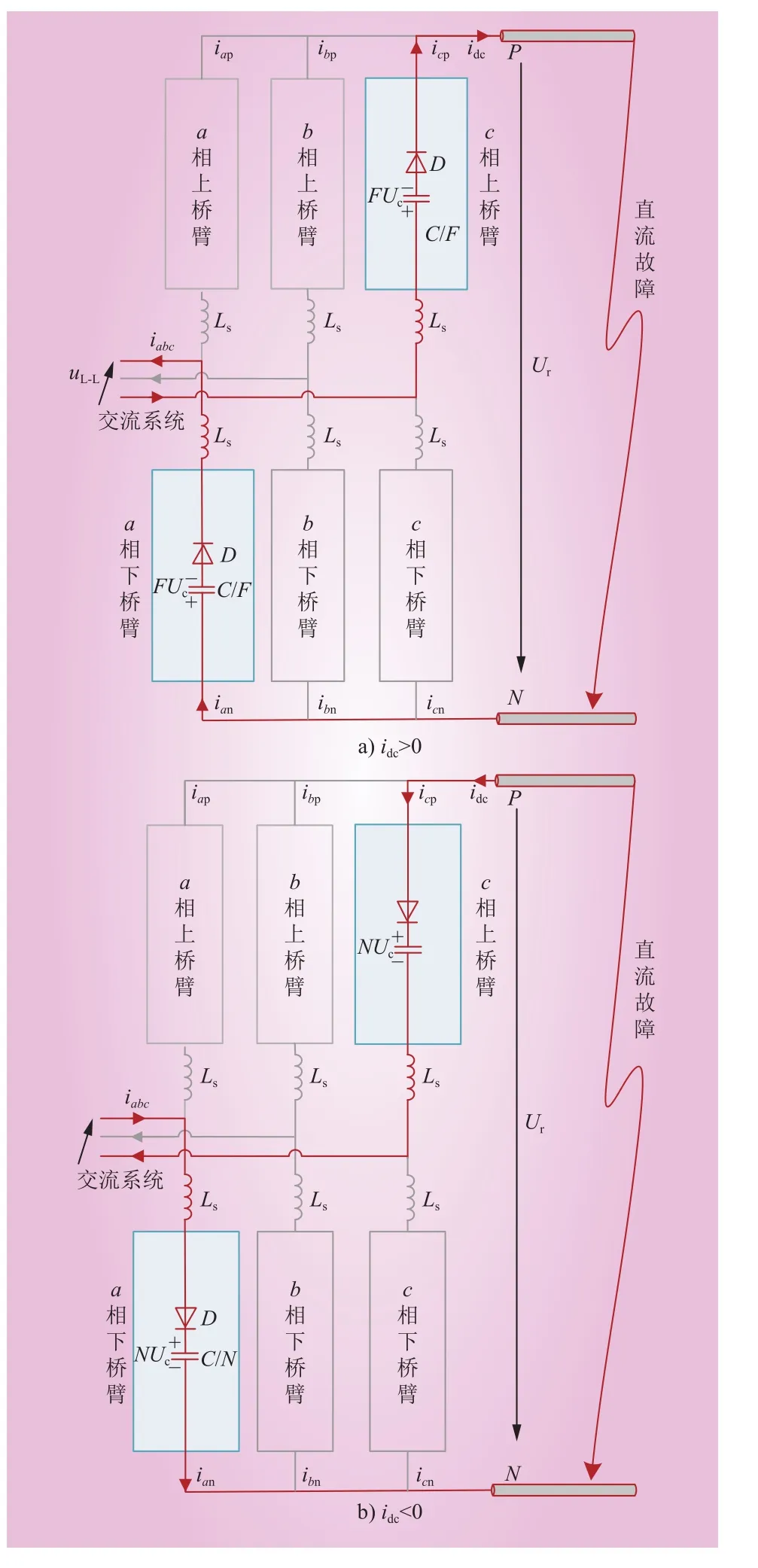
图4 直流故障电流通路Fig. 4 DC fault current path

如果桥臂电流为负方向，故障时刻电压为

式中：uL-L为系统交流侧的线电压；uD为存在故障电流时所有导通的二极管正向电压之和；Ur为系统直流侧的残压。

全桥子模块数目需要满足二极管具有反向截至电压，即

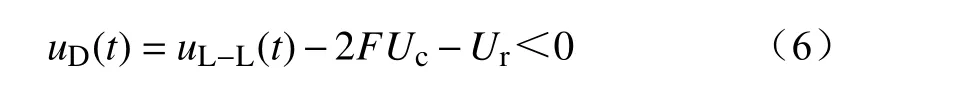
2.3 调制方式对调制比的影响

由于在运行过程中全桥子模块可以输出负电平，全桥子模块和半桥子模块的开关函数会有不同，所以混合型MMC的调制策略和传统的半桥型MMC调制方式也有不同[22-23]。无论使用哪种调制方法，半桥子模块都只有输出正电平或旁路2种情况。当调制比较大时，桥臂中的直流分量占主导，会使得桥臂电流变成单极性，桥臂电压和桥臂电流波形如图5所示。半桥子模块只有充电情况或者只有放电情况。为保持半桥子模块电容电压平衡，桥臂电流必须是双极性的，这一要求会限制混合型MMC的调制比。

图5 桥臂电压和桥臂电流波形Fig. 5 Arm voltage and arm current waveform

以a相上桥臂电流为例，直流电流是负方向，最大电流为正极性，电流关系为

MMC的输入功率和输出功率守恒，即

3 全桥子模块比例设计流程

直流牵引供电系统的全桥子模块比例设计流程如图6所示，具体步骤如下。

图6 全桥子模块比例设计流程Fig. 6 Design process of the proportion of full-bridge submodule

（1）通常桥臂电流峰值选择要小于开关器件连续直流电流的一半，本文根据常用开关器件电流等级选择桥臂电流峰值Iarm_peak，即

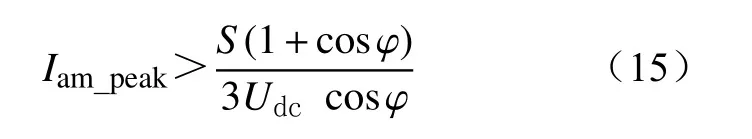
（3）根据开关器件的电流等级确定电压等级选择子模块电容电压Uc，通常子模块电容电压选择要小于开关器件额定电压的一半。本文中选择Uc时使得Udc为Uc的整数倍K。

（4）根据功率守恒计算出变流器的相电压峰值，即

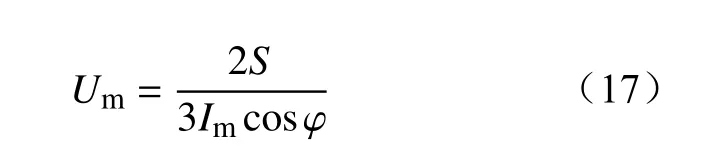
（5）计算出变流器的电压调制比，需要满足桥臂电流双极性条件m＜2。如不满足，则需要重新选取开关器件的电压和电流等级。

（6）桥臂中的模块数需满足最大负电压和最大正电压的输出能力，以及直流故障清除能力，即

根据计算出的K和m，求出变流器桥臂中子模块数量的最小值和全桥子模块数目的最小值，确定F和N。

4 算例分析

假设在城市轨道交通直流牵引供电系统中Udc为1 500 V，混合型MMC的额定容量为6 MV·A，稳态运行时负荷功率因数范围为0.9＜cosφ＜1。计算步骤如下。

（1）桥臂电流峰值需要满足Iarm_peak＞2 815 A，由于负荷电流较大，可用多只IGBT并联，Iarm_peak=3 000 A。

（2）计算Im=3 333 A。

（3）选择子模块电容电压Uc=750 V，K=2。

（4）变流器的相电压峰值Um=1 333 V。

（5）计算变流器的电压调制比为m=1.78，满足条件m＜2。

（6）根据前面所提的全桥子模块比例设计方法，N和F的关系为

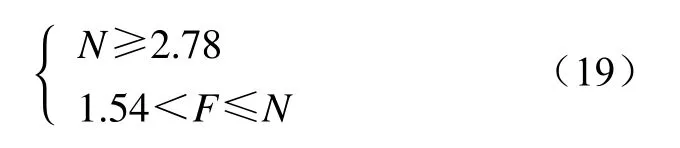
式(19)取整后为

虽然得到N和F的最小值，但是它们的取值结果依然有很多种选择。本文选择了3组参数，子模块数目如表1所示。在PSCAD中搭建仿真模型，验证稳态运行能力和直流故障清除能力，并根据仿真结果，比较桥臂子模块数量和全桥子模块数量变化时的影响。

表1 MMC桥臂子模块数目参数Table 1 Number of sub-modules in MMC arm

4.1 稳态运行和直流故障清除能力验证

混合型MMC的交流侧经过1个10 kV/1.63 kV的三相变压器与10 kV电力系统相连，在1.0 s时设置直流极间金属性故障，经过1 ms后MMC闭锁，观察故障前后的交流电压、交流电流、直流电压和直流电流波形，仿真结果如图7所示。

图7 混合型MMC稳态运行和直流故障清除仿真波形Fig. 7 Hybrid MMC steady state operation and DC fault clearing simulation waveform

当桥臂子模块数量N=4时，交流侧电流波形畸变严重，不满足10 kV系统的并网电流谐波含量要求。将全桥子模块数目从2增大到4后，即从混合型MMC变为全桥型MMC，交流侧电流波形依然没有改善。继续增加子模块数目，当桥臂内包含4个全桥子模块和2个半桥子模块时，交流电流波形得到明显改善。对交流电流进行快速傅立叶变换（FFT），具体结果如图8所示。总谐波畸变率从19%降低到2%。这说明在低电压大电流的城市轨道交通直流牵引供电系统中，根据混合型MMC全桥子模块比例的设计方法得到子模块总数的和全桥子模块数的最小值后，不能只考虑经济性，并不是子模块数越小越好。因为MMC的子模块数目很少，等效开关频率很低，谐波含量很大，并且负荷电流也很大，控制精度上稍有误差，就会引起很大的电压波动。当桥臂的子模块数目增多后，子模块电容电压波动减小，更有利于控制，电流波形质量得到改善。

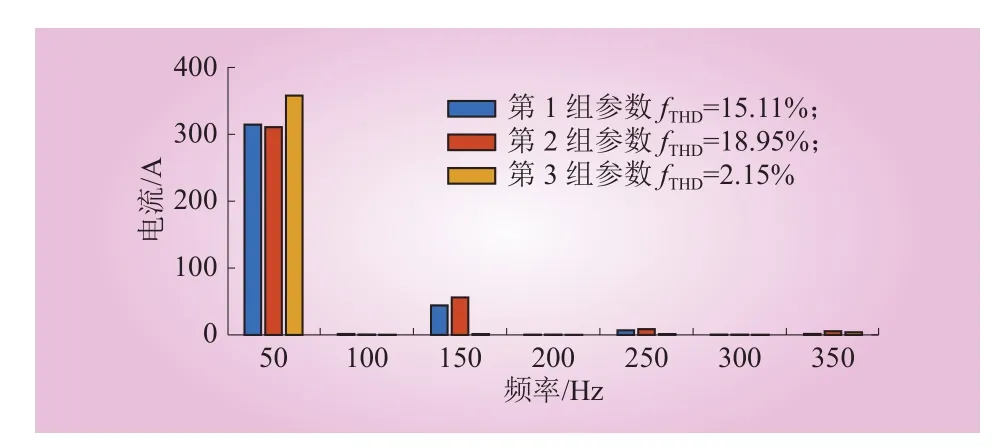
图8 交流电流FFT结果Fig. 8 FFT results of AC current

直流故障电流清除对比如图9所示。3组参数都可以清除直流故障。对比第1组参数和第2组参数，可以发现当全桥子模块数目增多，闭锁后交流回路中的反向电容电压增大，直流故障电流更快速地减小至0。对比第2组参数和第3组参数，全桥子模块数目没有增加，只有半桥子模块数目增加，仅在半个周波内反向电容电压增大，直流故障电流的衰减速度变化不明显。

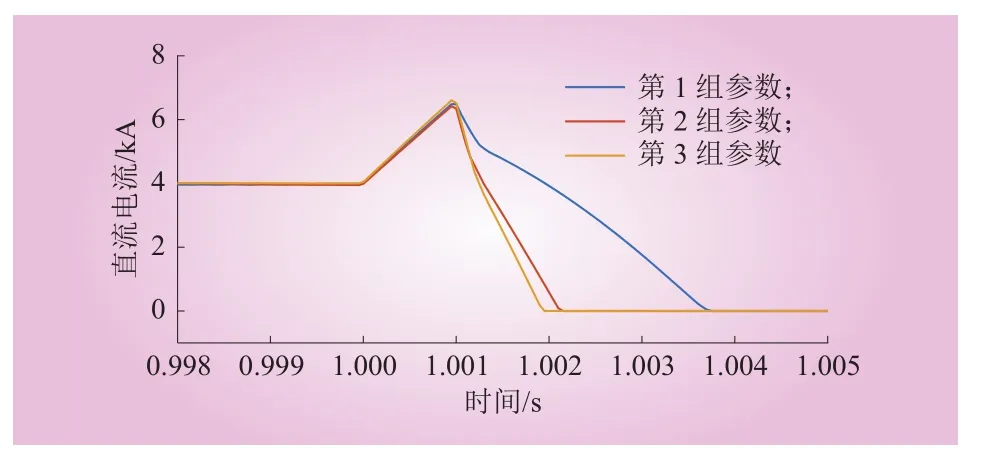
图9 直流故障电流清除对比Fig. 9 Comparison of DC fault current clearance

4.2 子模块数目对电容电压波动的影响

使用表1的3组参数，选择损耗较小的调制方式，采用电容电压排序算法，载波频率全都是15倍基频。当N=4时，子模块电容选择为30 mF；当N=6时，子模块电容选择为20 mF，以a相上桥臂为例，观察子模块电容电压、桥臂电流和桥臂电压，仿真结果如图10所示。

因为本算例中的调制比较大(m=1.78)，所以桥臂电流中直流分量较大而交流分量较小，桥臂电流大部分时候都处于负极性状态，根据电容电压排序算法，全桥子模块的电容电压波动较大，半桥子模块的电容电压波动较小且投入的时间较少。

在图10 a)中，电容电压最大值约0.87 kV，最小值约0.7 kV，波动可达到11%，全桥子模块投入时，电容电压波动较大，全桥子模块和半桥子模块都投入时，由于总电容数的增加，电容电压波动较小。在图10 b)中，桥臂中的半桥子模块全部替换成全桥子模块，电容电压波动情况一致，电容电压最大值约0.85 kV，最小值约0.7 kV，电压波动为9.7%，略有减小。当使用第3组参数时，可以进行交替充放电的电容数目增多，充放电过程减缓，电容电压最大值约0.82 kV，最小值约0.72 kV，电容电压的波动减小为6.5%。由图10可知，当桥臂子模块数目N恒定时，增加全桥子模块的比例对电容电压波动抑制的效果有限，当新增半桥子模块数目后，电容电压波动会有明显减小的趋势。

图10 子模块电容电压波动仿真波形Fig. 10 Submodule voltage fluctuation simulation waveform

5 结论

本文针对城市轨道交通直流牵引供电系统的特点，提出适用于低电压大电流系统的混合型MMC供电方案，对全桥子模块比例的设计方法进行了分析，给出设计流程。全桥子模块比例的设计既要满足稳态运行的需求，也要满足直流故障清除能力的需求。全桥子模块比例的设计还和MMC稳态运行时的调制比直接相关，MMC长期处于调制比大于1的运行工况，为满足半桥子模块电容的充放电平衡，对调制比的设计也有一定的要求。本文选择常见的1 500 V直流牵引供电系统作为算例，得到子模块总数和全桥子模块数目的取值范围，选取了3组参数，在PSCAD软件中搭建仿真模型进行分析，比较了在满足设计需求的条件下，不同参数所造成的影响，为MMC其他主回路参数的选型提供了参考。