基于MSSST和强化轻量级卷积神经网络的有载分接开关运行工况识别

魏 敏，王刘旺

（1.国网浙江省电力有限公司嘉兴供电公司，浙江 嘉兴 314033；2.国网浙江省电力有限公司电力科学研究院，杭州 310014）

0 引言

作为大型变压器中的关键部件组成，有载分接开关承担着无功调节和稳定功率的重要功能，由于实际工程现场分接开关切换十分频繁，其故障发生率一直居高不下。异常工况下的分接开关对于变压器稳定运行形成了巨大的安全隐患，若不及时甄别处理，很容易引发电网连锁事故，因此有载分接开关工况识别对于保障整个电力系统安全可靠运行具有重要意义［1-2］。

近些年，相关领域学者围绕着有载分接开关工况甄别开展了大量研究工作，相继提出了油液溶解气体分析［3］、电弧监测［4］、声学分析［5］、温度分析［6］等一系列工况识别策略。有载分接开关切换过程属于瞬态触发动作，机构各部件间的摩擦碰撞将导致非平稳非线性振动，所拾取的振动信号中包含丰富的状态信息，因此振动分析已成为分接开关状态监测的重要技术手段［7-8］。

不同运行工况下，分接开关切换过程产生的时域振动信号差异性较小、可区分性较差，相比于单一时域特征，通过合理的时频分析手段将原始时域特征转化为物理意义更为明确的二维时频特征，可放大信号特征间的差异，便于后续状态分类辨识。现有文献报道中，STFT（短时傅里叶变换）、CWT（连续小波变换）、WVD（魏格纳威尔分布）是常用的变换域特征处理手段，但存在时频聚焦性不足、分析灵活性欠佳的弊端。最近，相关学者提出一种MSSST（多重同步压缩S变换）理论［9］，其本质是在ST（S 变换）基础上进行多重同步压缩处理，从而获取能量更为集中、表达更为清晰的二维时频特征。本文从描述振动信号时频特征角度出发，将MSSST理论引入电气设备状态监测诊断领域，用于提升信号特征表达维度，充分挖掘分接开关振动信号中蕴含的特征信息。

近些年，深度学习理论在生物特征识别、大数据信息挖掘等领域迅速普及，作为深度学习理论中最具代表性的网络结构框架，CNN（卷积神经网络）在电力设备状态监测诊断领域也得以成功应用［10］。经典的CNN 运算量及模型参数数量较大，对计算机硬件水平及存储空间要求较高，而实际工程现场设备的计算能力及存储空间有限，因此CNN 的固有缺陷限制了其在工程现场的普及应用［11］。为了弥补这一缺陷，Howard［12］通过一种新颖的分离卷积操作替换标准的卷积运算，在传统CNN 模型基础上开发出MobileNetv1 轻量级CNN模型，可有效缩减模型参数数量及训练时间，但是存在输入层内核数量固定的瓶颈。最近，Sandler 等人［13］提出一种MobileNetv2 轻量级CNN模型，其最大亮点是能够在保证计算精度前提下大幅提升训练效率，因此本文尝试将其引入电气设备状态监测诊断领域，并在该模型基础上融合Adaboost 自适应提升机制，提出一种分类能力更为优良的RLCNN（强化轻量级卷积神经网络）模型。

基于以上阐述，本文利用MSSST将一维时域振动波形转换为二维时频域图像，扩充特征表达维度后，通过RLCNN 模型对图像进行层次化的解析及分类，提出一种新颖的变压器有载分接开关多工况识别方法。该方法充分发挥了MSSST算法在信号时频特征刻画上的优势以及RLCNN 模型在多状态分类方面的强大性能，有望实现变压器有载分接开关运行工况的准确判定。

1 MSSST

1.1 MSSST基本原理

对于一个给定信号x(τ)，其ST表达式为［9］：

由式（1）可知，ST 的窗函数比较灵活，其宽度可根据分析频率ω的变化而变化，在低频区域窗宽较大而在高频区域窗宽较窄，但ST的时频聚焦性仍不够理想，存在一定提升空间。为此，相关学者借鉴多重同步压缩变换的思想，在ST基础上进行多重同步压缩处理，提出了MSSST 算法，具体表达式为：

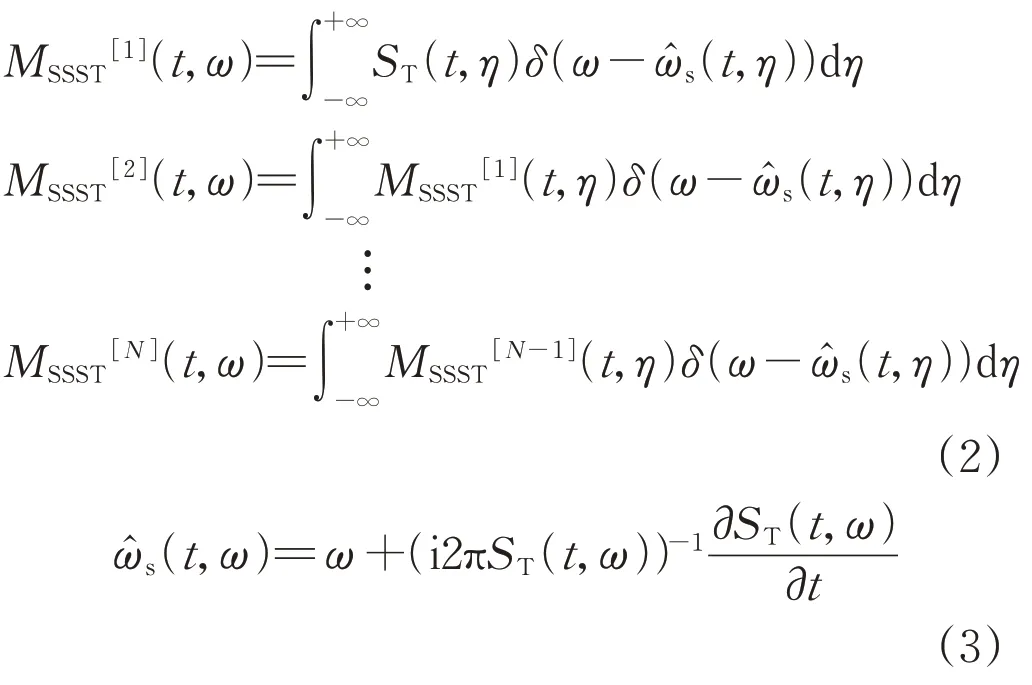
式中：δ(·)为狄拉克函数；η为表达式变换中间变量；MSSST[N](t，ω)为通过同步压缩算子迭代N次所得结果；(t，η)为瞬时频率估计值。将MSSST[1](t，η)代入MSSST[2](t，η)可得：

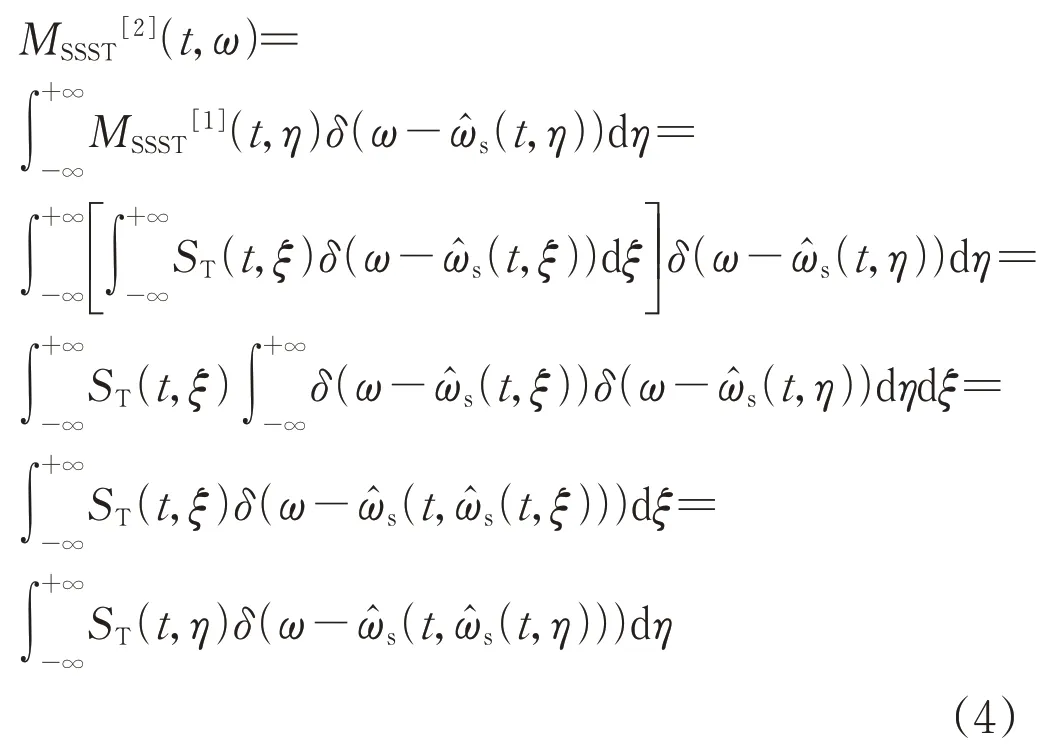
式中：ξ为表达式变换中间变量。

与上述过程相似，利用同步压缩算子迭代N次后，时频能量重分配结果可表示为：

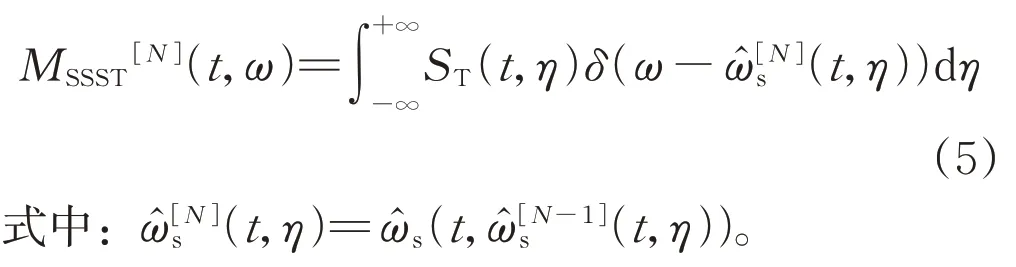
每一次迭代运算，MSSST通过构造一个新的瞬时频率估计值来实现模糊ST 能量的重排分布，经过多次迭代运算，所得瞬时频率估计值逐渐接近原始信号的真实频率，从而有效提高二维图像的时频聚焦性。与STFT、CWT、WVD 等时频分析方法类似，利用MSSST算法对一个给定信号进行分析处理，所得二维图像MSSST[N](t，ω)反映了在任意时间点t及频率点ω处信号的能量强度。

1.2 MSSST时频分析能力验证

为验证MSSST算法的时频分析能力，模拟生成一个多分量瞬态冲击响应信号m（t）：

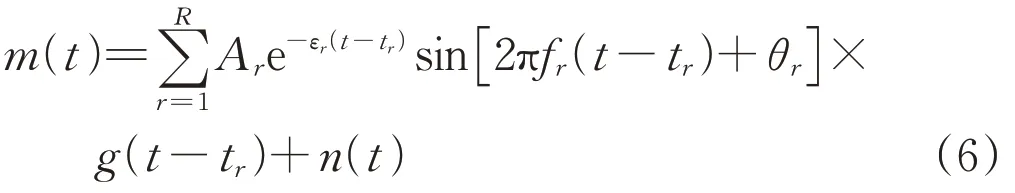
式中：R为瞬态冲击响应分量个数；g（t）为阶跃响应函数；Ar、εr、fr、tr、θr分别为第r个响应分量的振动幅值、阻尼系数、振动频率、发生时刻、初始相位；n（t）为添加的高斯白噪声。

设置m（t）的数据点数Ns=1 800，采样频率fs=6 000 Hz，信号时长为0.3 s，所添加高斯白噪声n（t）均值为0、标准差为0.05。本文利用3 个瞬态冲击响应分量来构造模拟信号m（t），即R=3，这3个分量的相关参数设置如表1所示。为了增大信号时频特征分辨刻画的难度，设置这3个瞬态冲击响应分量在时域上相互交叠，均产生于0.1 s时刻。

表1 模拟信号参数设置

模拟信号波形及频谱如图1所示：时域波形呈现为能量逐渐衰减状态，较为简单；频域分析中出现了3个明显的谱峰，分别对应模拟信号中包含的300 Hz、1 100 Hz、1 600 Hz频率成分。

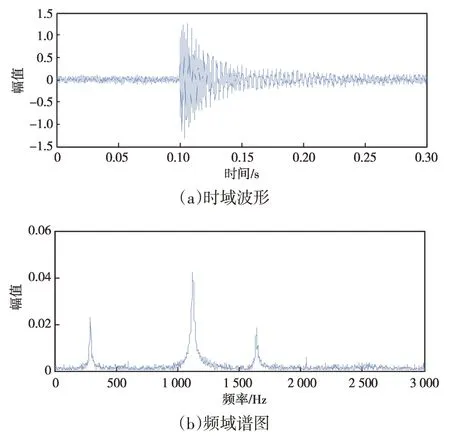
图1 模拟信号波形及频谱

分别利用MSSST、ST、MSST（多重同步压缩变换）、STFT、CWT、WVD 等时频分析方法对该模拟信号进行分析处理，用于对比验证MSSST算法在时频特征刻画方面的优势，结果如图2所示，为了更为清晰地对比分析，仅展示了时间轴0.08～0.18 s、频率轴0～2 000 Hz范围内的时频特征。通过观察可以发现：MSSST算法所得分析结果时频聚焦性最佳、分辨率最高，模拟信号中包含的3个频率成分均被清晰准确表达，并且没有多余背景干扰成分；MSST和CWT算法虽然也能够分辨出模拟信号中时域相互交叠的3个频率成分，但是分析效果与MSSST 相比存在一定差距；ST、STFT、WVD 算法所得分析结果则不够理想，聚焦性差、频率成分交叉等因素导致未能准确表达原始信号的时频特征。

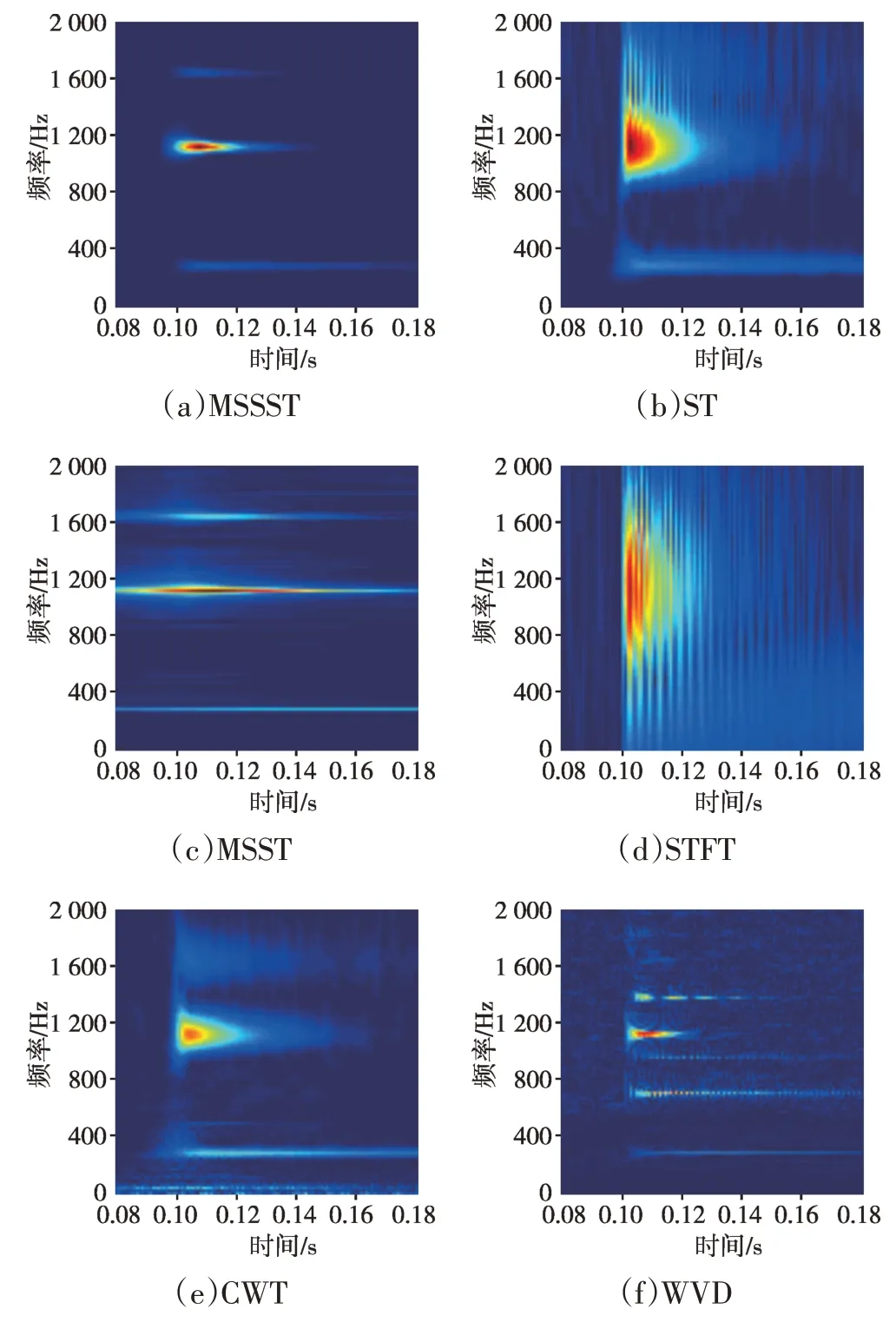
图2 模拟信号不同时频分析方法处理结果

为进一步定量评价MSSST算法的性能，本文利用Rényi熵指标对不同时频分析方法所得结果进行量化计算对比。Rényi熵指标是信息评价标准中衡量二维图像复杂度的最佳通用指标，对于任意一个二维图像，如果所得熵值越小，表明图像混乱程度越低，能量聚焦性越好；反之熵值越大，表明图像混乱程度较高，能量聚焦性较差。Rényi熵Ra的计算表达式为［14］：

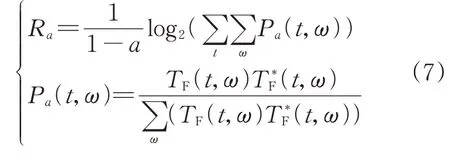
式中：a为Rényi 熵的阶次；Pa(t，ω)为单位能量信号的概率分布函数；TF(t，ω)为时频分布系数，(t，ω)为TF(t，ω)的共轭。

借助式（7）分别计算图2 中各个二维时频图像对应的Rényi 熵值，本文取Rényi 熵阶次a=3，所得结果如图3 所示。图3 中，MSSST 算法所得时频分析结果对应的熵值明显小于其他对比方法，表明通过MSSST所得时频分析结果能量聚焦特性最佳，能够更清晰、准确地表达信号时频特征。

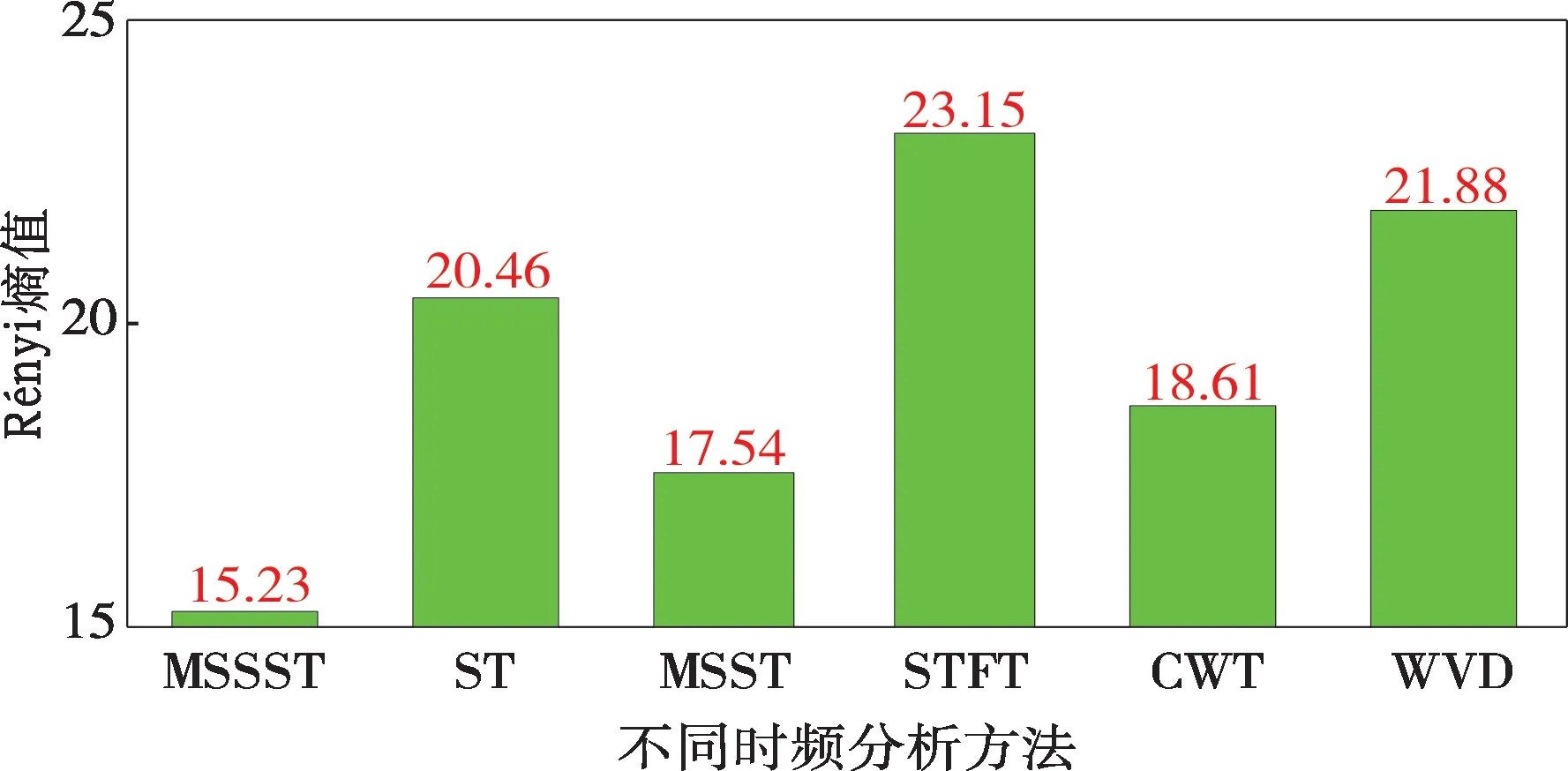
图3 不同时频分析方法Rényi熵值

2 RLCNN

2.1 MobileNetv2轻量级CNN

作为一种代表性深度学习框架，CNN 模型通过构造多个卷积核并结合稀疏连接、权重共享、时空域降采样，对输入样本进行逐层卷积运算及池化处理，从而实现样本隐含拓扑结构特征的逐级提取。CNN 模型主要由图4 所示输入层、卷积层、池化层、扁平层和全连接层构成。卷积层由多个卷积核组成，每个卷积核中元素分别对应一个权重值和一个偏差量，对输入样本进行卷积运算能够快速挖掘其隐含特征；经由卷积层所挖掘的样本特征被输送到池化层实现参量缩减，处理方式包括最大池化、平均池化等；池化层处理后的数据被进一步输送到扁平层，实现多维至一维向量的转换；最后，通过全连接层获取最终所需结果［15］。

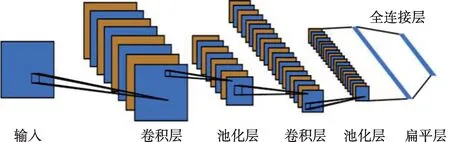
图4 CNN模型

传统CNN模型参数数量及运算量庞大，所需存储空间较大，对硬件配置要求较高，不利于工程现场普及应用。而MobileNetv2 轻量级CNN 模型在卷积运算时采用一种具有线性瓶颈单元的逆向残差结构（如图5所示），相较于分离卷积操作运算量更小、准确率更高，该模型能够在计算速度和识别准确率之间寻求最佳平衡，有利于其在工程现场计算平台中推广应用。

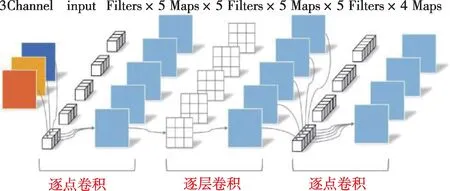
图5 MobileNetv2模型卷积运算

2.2 Adaboost自适应提升机制

Adaboost 自适应提升机制的核心思想是在训练样本集中生成一系列权重系数，在此基础上对训练样本集进行调整以生成多种假设条件，通过增大前一个网络模型错分样本的权重来提高下一个网络模型的识别准确率，因此该机制能够充分利用有限训练样本集获得更好的识别效果［16］。Adaboost 在迭代运算过程中，利用多分类指数损失函数的阶段性加法建模，并依据训练样本集加权误差最小化原则不断更新权重系数。随着迭代过程不断推进，正确识别的样本集权重逐渐减小，而被误识别的样本集则被赋予更大权重。其实现步骤概述如下：

步骤1，假设训练集样本类别k=1，2，…，K，样本数为V，初始化训练集权重ωi=1/v（v=1，2，…，V）。

步骤2，设置最大迭代次数为M，执行m=1～M的迭代运算过程。

1）利用权重为ωi的训练集训练网络模型Tm(·)。

2）计算识别误差err，m：

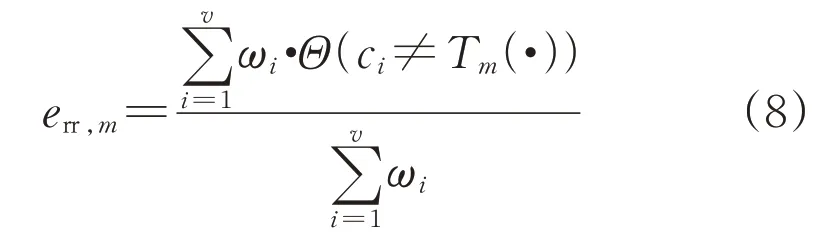
式中：ci为实际类别标签；i代表标签序号；v代表样本序号；Θ(·)为指示函数，括号中内容为真时取值为1，反之指示函数取值为0。

3）根据所得识别误差重新计算权重系数：

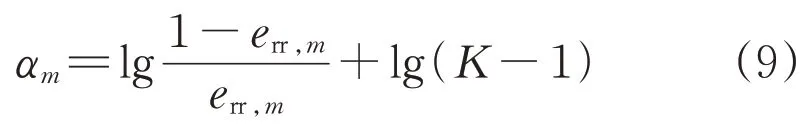
式中：αm为权重系数。

4）更新权重：

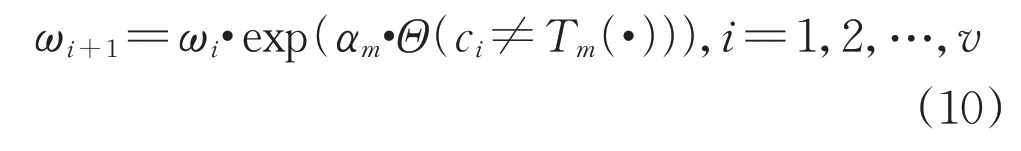
5）对权重进行归一化处理。

步骤3，获得最终识别结果C：

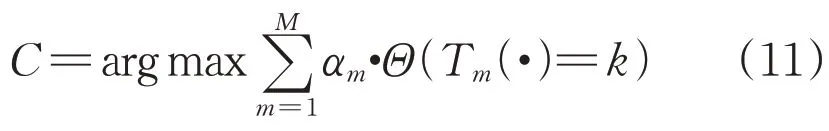
2.3 基于MobileNetv2-Adaboost 的RLCNN模型

实际工程中，神经网络模型的训练效果通常受数据集样本大小、维度及总量的影响，为了在有限训练样本集条件下获得最佳识别效果，提高变压器有载分接开关不同运行工况的辨识准确率，本文结合Adaboost 自适应提升机制在集成学习方面的能力，以及MobileNetv2 轻量级CNN 在图像识别领域的优势，提出一种基于MobileNetv2-Adaboost 的RLCNN 模型，该模型通过Adaboost自适应提升机制对多个MobileNetv2网络进行强化学习训练，并将所有网络输出结果按不同权重进行组合，从而获得更高的识别准确率，RLCNN实现流程如图6所示。

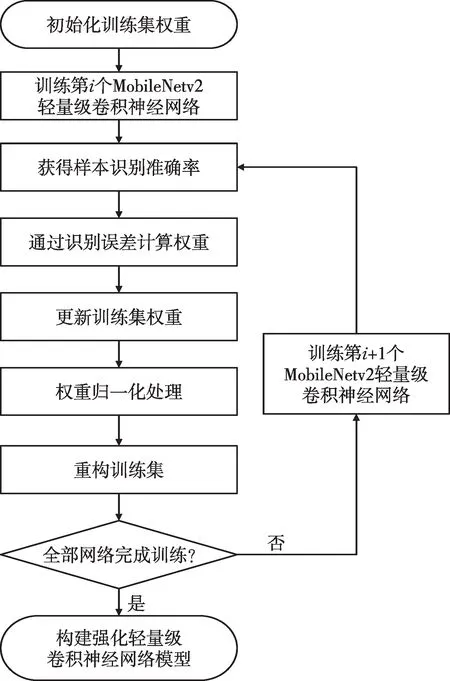
图6 RLCNN模型实现流程

3 实验验证

3.1 数据采集

为了验证本文所提识别方法的有效性，在CM型110 kV 有载分接开关工况模拟实验台上开展实验研究。实验台结构如图7（a）所示，主要包含油箱、齿轮盒、电动机构、绝缘筒、分接选择器、切换开关。分别设置分接开关正常运行、主弹簧松动、主触头磨损和传动机构卡涩4种类型的运行工况。振动传感器采用东华1A110E型压电式加速度传感器，该传感器具有分辨率高、抗干扰能力强的优点。采用粘合安装方式将压电加速度传感器布置在分接开关顶端及侧壁位置，如图7（b）所示，用于采集开关切换动作产生的振动信号，设置采样频率为20 kHz，利用NI9234 采集卡实现模/数转换后输入到计算机中进行数据存储及后续分析处理。实验过程中，将分接开关置于充满油液的油箱中，模拟分接开关在变压器油箱中的运行环境，使振动信号更接近实际工程环境。

图7 有载分接开关实验台

整个实验过程中，通过加速度传感器分别采集分接开关正常工况及3种故障工况产生的振动信号，每种工况取500组样本信号，每组样本信号包含10 000个数据点，整个数据集共包含2 000组样本。从中随机抽取80%样本作为训练集用于训练RLCNN 模型参数，剩余20%样本作为测试集用于评估本文所提方法的识别能力，因此构造的训练集样本为1 600 组，测试集样本为400 组。图8为分接开关不同工况下测取的样本信号时域波形及频域谱图，其中g为重力加速度。通过对比可以发现，分接开关传动机构卡涩样本波形与其他运行工况下的波形存在一定差异，而正常工况与主弹簧松动、主触头磨损工况下切换动作所产生的样本信号波形及谱图的差异不明显。尤其是正常工况和主触头磨损工况相比，二者的样本信号波形及谱图极为相似，究其原因主要由于触头磨损对于分接开关整体动态特性所造成的影响不明显。总体来看，仅凭借时域波形及频域谱图观察难以进行特征捕捉，无法快速有效地区分出有载分接开关的不同运行工况。

3.2 分接开关工况辨识

下面利用本文提出的方法对变压器有载分接开关运行工况进行自动辨识。首先，利用MSSST时频分析算法对样本信号进行处理，将一维时域波形转换为二维时频图像，实现特征增维，便于后续RLCNN模型的训练及测试。以图8中分接开关不同工况样本信号为例，经MSSST处理后所得结果如图9所示，为了表达更为清晰，仅展示时间轴0.05～0.3 s、频率轴0～8 000 Hz 范围内的时频特征。对比后可发现：有载分接开关正常工况下切换动作所产生的振动信号能量主要分布在0～2 000 Hz及4 000～6 000 Hz范围内；主弹簧松动状态下机构刚度有所下降，振动信号能量分布稍有偏移，主要分布在0～2 000 Hz 及4 500～7 000 Hz 范围内；分接开关主触头磨损状态对于机构整体动态特性影响较小，其时频分析结果与正常工况下所得结果十分相似；传动机构卡涩状态下，分接开关完成整个切换动作所需时间有所延迟，能量分布主要集中在3 500～6 500 Hz 范围内，不同工况样本所呈现的二维时频图差异性更大，可区分性有所提升。

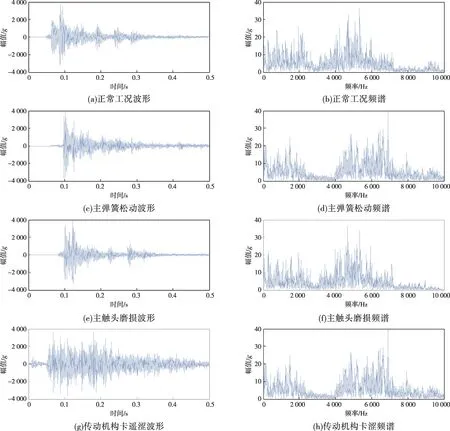
图8 不同工况样本波形及频谱

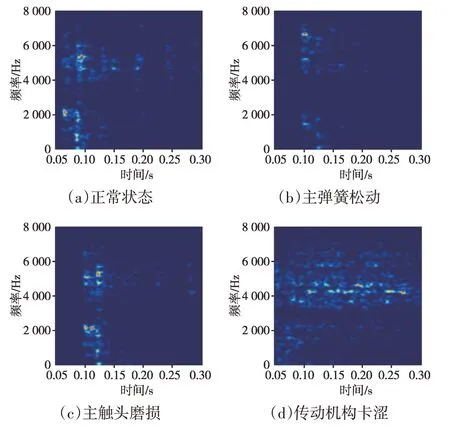
图9 不同工况样本MSSST处理结果

利用Python 编程语言在Windows 平台上搭建RLCNN 模型，相应的计算机硬件水平为Intel Core i7-8700k 处理器、32 GB 内存环境、Nvidia GTX 1080Ti GPU。参考文献［11］对单一Mobile⁃Netv2网络结构参数进行设置，具体参数设置情况如表2 所示。其中扩展因子可调整输入图像尺寸，除第一层外其他层步长均设置为1，空间卷积运算均使用3×3卷积核。

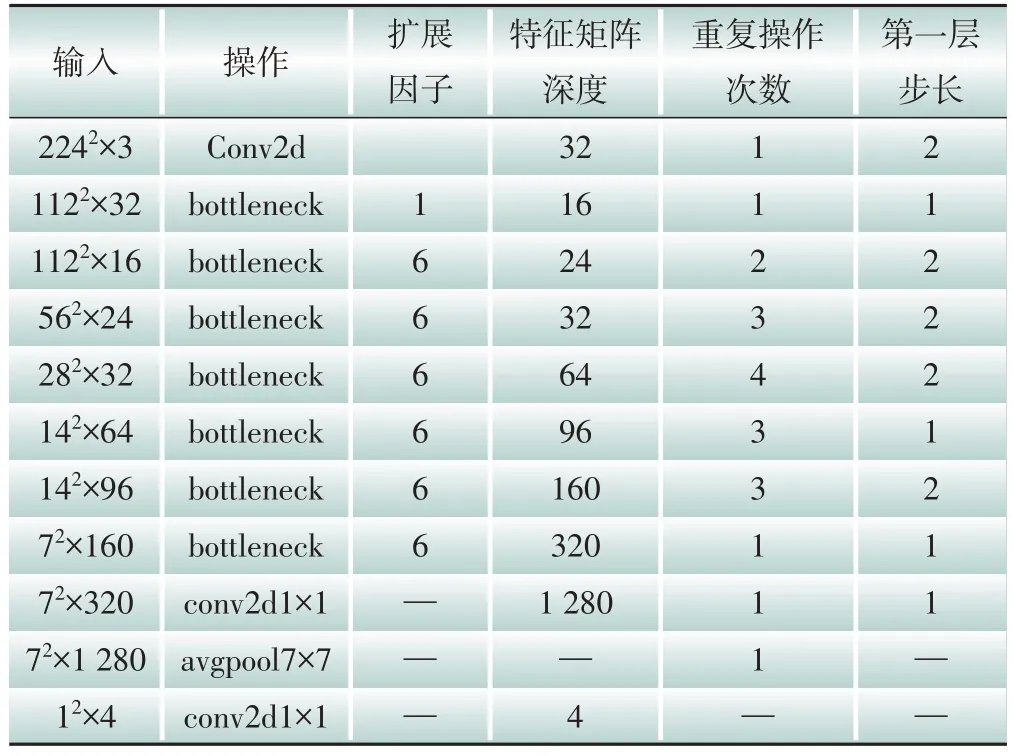
表2 MobileNetv2网络结构参数

全面考虑训练集样本数量、类别及长度、网络结构复杂度、计算机内存大小、处理器性能等诸多影响因素，本文对网络模型超参数设置情况如下：在不爆显存条件下，应该尽可能地选用较大的批数据尺寸，在此设置单一MobileNetv2网络批数据大小为32；学习率的选取则参考文献［13］，直接设置为0.000 1；在训练过程中利用Model⁃Checkpoint函数在每个迭代周期后检查模型识别准确率是否提升来保存最佳模型，最终设置迭代轮次为40，可防止因迭代次数过多而造成的过拟合现象；由于样本集包含了分接开关4种不同状态样本，因此样本类别数为4；损失函数选取为交叉熵。

构建RLCNN 模型时，需要通过Adaboost 自适应提升机制集成多个MobileNetv2网络，由于目前缺少理论借鉴及相关文献报道参考，本文通过多次实验来确定网络数量。对比发现，当MobileNetv2网络数量为5时，所构建RLCNN模型的识别准确率达到稳定状态，之后随着网络数量增大，准确率不再出现明显提升。因此，综合考虑模型的可靠性及运算负担，本文利用5 个单一MobileNetv2网络进行集成来构建RLCNN 模型。在Adaboost迭代运算过程中，通过训练样本集加权误差最小化原则来不断更新各个单一MobileNetv2网络的权重系数，训练结束后各个网络可自动获得其最佳权重配比，从而使得所构建的RLCNN 模型具有良好的整体识别性能。

利用MSSST算法处理所得样本信号获取二维时频图像后，将其输入到RLCNN 模型中进行训练及测试。为了保障识别结果的可靠性，在网络参数相同条件下识别30 次，并计算识别结果的平均值，最终测试集样本的平均识别准确率高达99.32%。为验证基于Adaboost自适应提升机制的RLCNN 模型的优势，绘制出单一MobileNetv2 网络在训练集和测试集上的识别准确率及损失值，如图10和图11所示。从图中可以看到，随着轮次的增加，训练集和测试集样本的识别准确率均逐渐增大，到第25轮时识别准确率接近95%后不再提升，而训练集和测试集样本的损失值也在第25轮时处于收敛状态，下降至0.1后不再变化。就呈现结果来看，单一MobileNetv2网络的识别效果仍存在一定提升空间，而通过Adaboost 自适应提升机制将多个轻量级CNN 进行融合，所构建的RLCNN模型则优势更加明显。

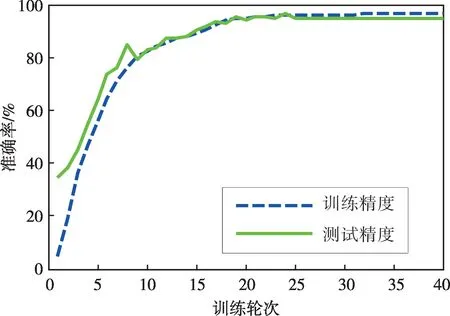
图10 单一MobileNetv2网络训练及测试准确率

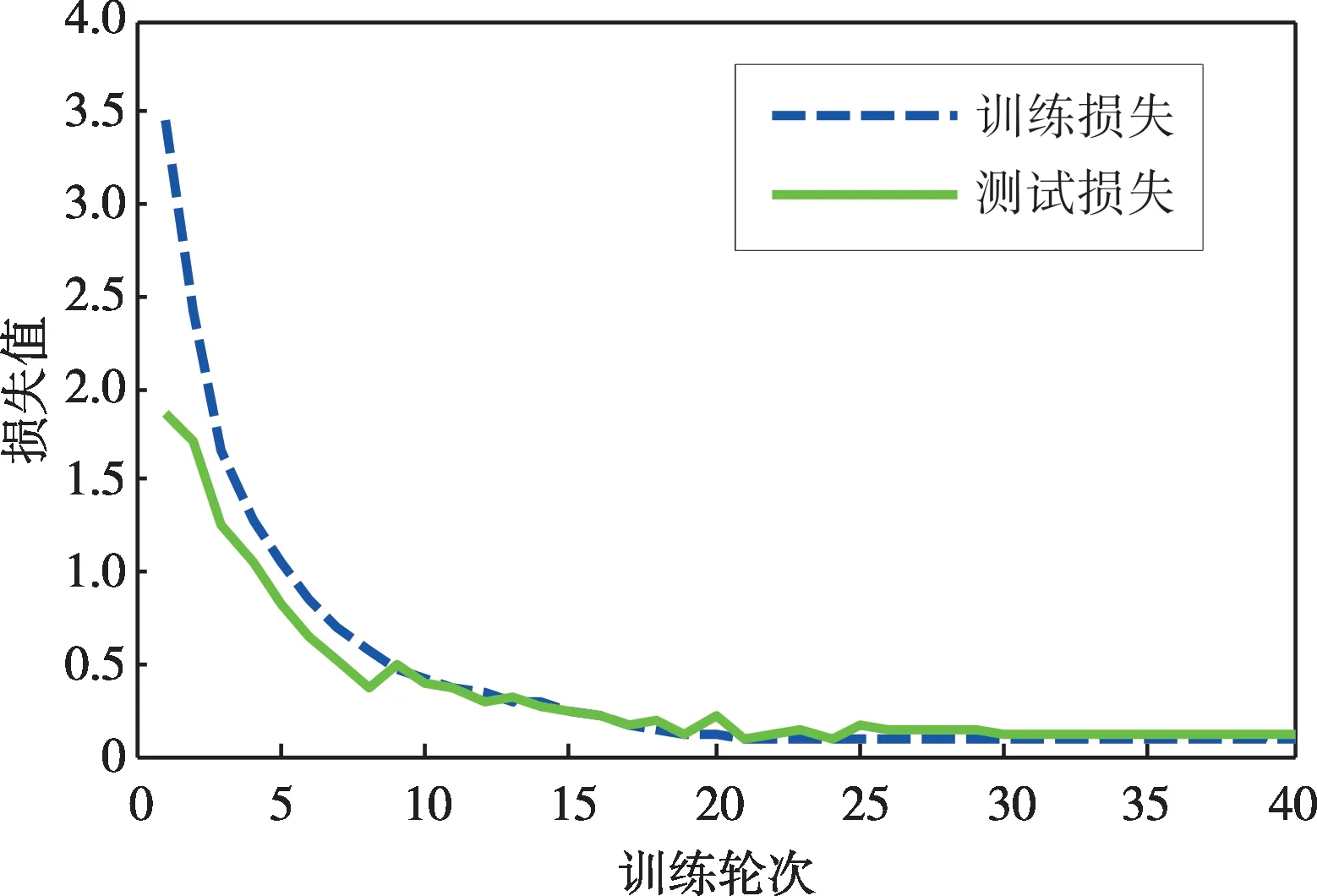
图11 单一MobileNetv2网络训练及测试损失值

3.3 方法对比研究

为了验证MSSST算法在分接开关振动信号时频特征提取方面的优势，分别利用MSSST、MSST、CWT、ST、STFT 和WVD 等时频分析方法对分接开关正常及故障运行工况下拾取的样本信号进行处理，并将所得时频图像输入到RLCNN模型中进行测试。在参数相同条件下识别30 次来保障对比结果的准确性，所得结果如图12及表3所示。其中利用MSSST算法提取样本时频特征后，RLCNN模型的平均识别准确率最高，达到99.32%，比MSST、CWT、ST、STFT、WVD算法分别高6.81%、12.18%、19.55%、22.93%、34.64%。此外，利用MSSST 算法进行时频特征提取，RLCNN 模型30 次识别结果的标准差仅为0.359，均小于其他时频分析算法识别结果的标准差，由此表明MSSST算法提取出的时频特征更加稳定、鲁棒性更佳。

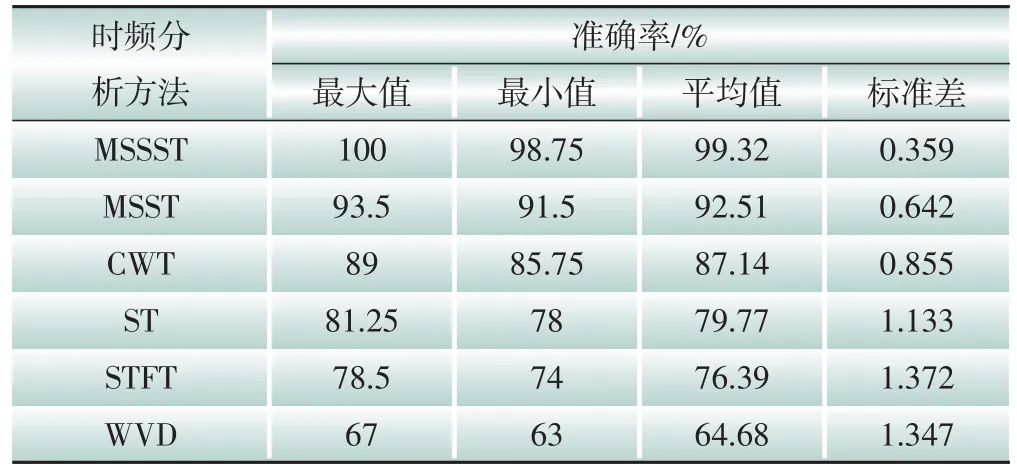
表3 不同时频分析方法准确率对比

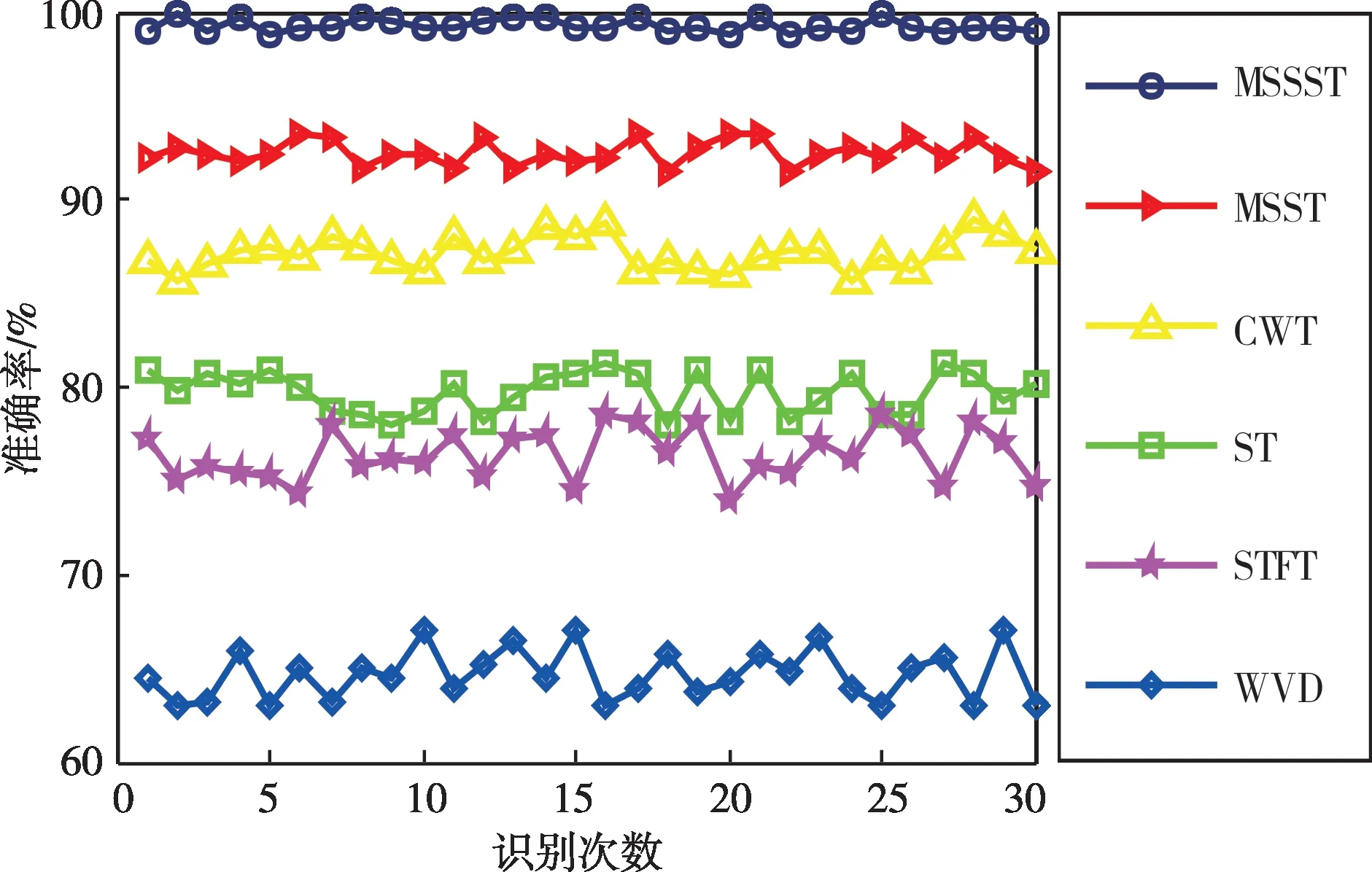
图12 不同识别次数准确率对比

为了验证本文所提有载分接开关工况识别方法的优越性，分别利用单一MobileNetv2 模型、CNN模型、ELM（极限学习机）［17］、SVM（支持向量机）［18］、BP（反向传播）神经网络［19］来识别分接开关的运行工况，设置5种对比方法与本文所提出的识别方法进行比较，见表4。与RLCNN模型相同，单一MobileNetv2 模型以及CNN 模型均可以直接从二维时频图像中自动提取特征信息，因此可将MSSST处理所得结果直接作为模型输入，而传统的ELM、SVM、BP 分类器则无法像深度学习网络模型一样自动读取并捕捉二维时频图像的特征，需要人为干预构造合理的特征向量作为输入才能够对其进行训练。在现有文献报道中，多尺度熵算法已被大量用于描述信号动态特征，在电力设备状态监测诊断领域具有诸多成功应用案例，并获得了广泛认可，因此本文计算有载分接开关不同运行工况下样本信号的MPE（多尺度排列熵值）［20］作为ELM、SVM 和BP 模型的特征向量输入。

表4 6种识别方法比较

在训练集/测试集数量比为4∶1 条件下，即训练集样本1 600 个、测试集样本400 个，分别利用6 种方法识别30 次并计算准确率均值，最终结果图14所示。从图中可以看出，本文提出的方法（方法1）识别准确率最高，达到99.35%，而方法2—6的识别准确率均值分别为94.76%、95.21%、89.34%、88.27%、84.63%，均低于本文所提方法。在训练速度方面，RLCNN、MobileNetv2、CNN 深度学习模型内部包含大量的网络参数，因此相比于传统的ELM、SVM、BP 机器学习模型所需训练时间明显增多。需要指出的是，传统CNN深度学习模型参数大小为550 MB，单一Mo⁃bileNetv2网络模型参数大小仅为13.5 MB，而由5个单一MobileNetv2网络所构造的RLCNN 模型参数大小也仅为67.5 MB，与传统CNN 深度学习模型相比，在保证识别精度的前提下网络规模明显减小。当图14 中的不同方法完成训练后，应用于测试样本识别时所需时间相差不大，以任意一个随机样本为例，分别利用方法1—6 对其工况进行识别，计算耗时分别为0.75 s、0.64 s、0.88 s、0.21 s、0.27 s、0.39 s，均能够满足实际工程现场需求，但是本文所提方法能够获得最高的识别精度。因此，综合对比分析，本文提出的方法具有明显优势。

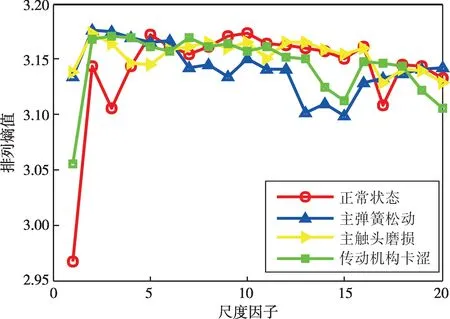
图13 不同工况样本MPE曲线

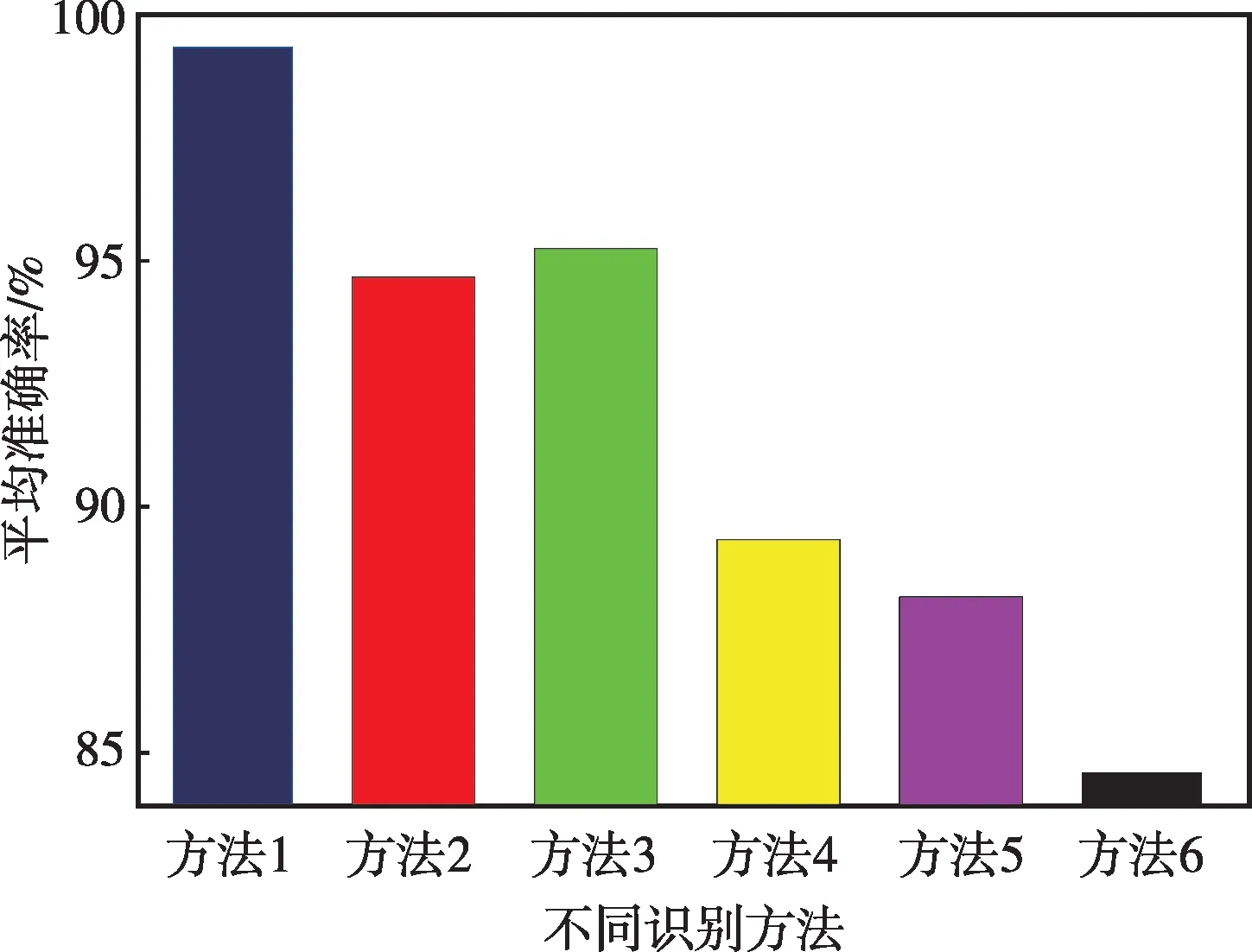
图14 不同识别方法平均准确率

为了进一步验证本文所提识别方法的稳定性，从2 000个样本集中随机抽取出不同数量的训练样本，针对分接开关4种运行工况状态，分别组成数量比为3∶1、2∶1、1∶1、1∶2 的训练集和测试集，如表5所示。利用表5中不同比例条件下的样本集对图14 中的6 种识别方法进行训练及测试，所得平均准确率统计结果如表6所示。整体来看，无论在何种比例条件下，本文方法的识别准确率均优于其他对比方法。由表6的比较结果可以进一步看出，随着训练集样本的减少，所有识别方法的平均识别准确率均有所下将，但本文方法的识别准确率并未像其他对比方法一样出现显著下降。即使在训练集样本数明显小于测试集样本数时（数量比为1∶2），本文方法的平均识别准确率仍能达到91.76%，而其他方法的平均准确率分别为82.38%、83.69%、76.51%、73.27%、61.87%，表明利用本文方法进行分接开关运行工况识别时，稳定性较好。究其主要原因在于以下两个方面：MSSST时频分析方法可以从原始振动信号中捕捉到敏感的差异性时频特征，为后续模型的工况识别奠定了良好基础；在MobileNetv2 网络中引入了Ada⁃boost 自适应提升机制，该机制通过逐步构造更为困难的学习问题，能够在少量有限数据集条件下有效实现模型的强化训练，从而获得更为强大的分类能力。

表5 不同比例的训练集、测试集组成

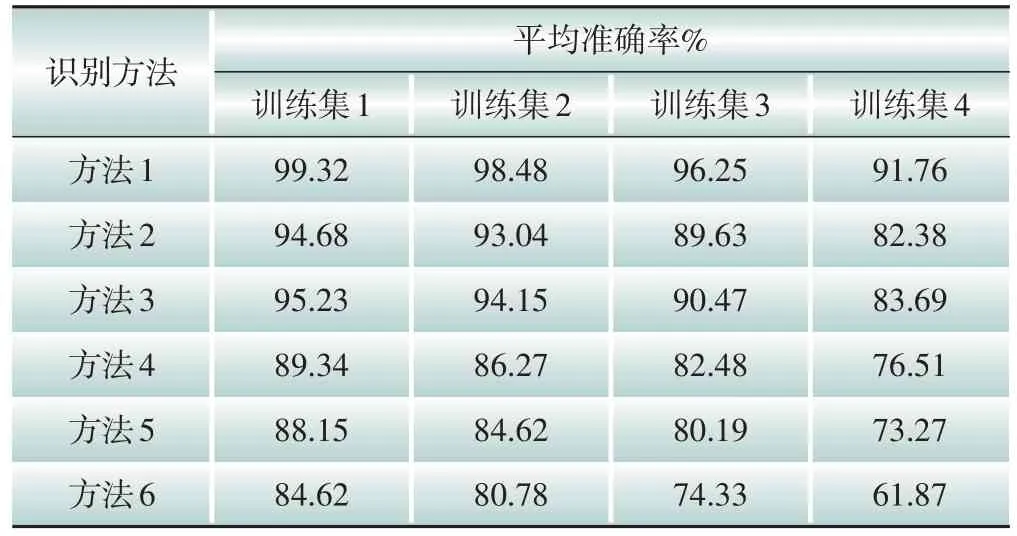
表6 不同识别方法下各训练集平均准确率

4 结语

针对有载分接开关运行工况识别问题，本文提出一种基于MSSST和RLCNN的识别方法，所得结论如下：

1）利用MSSST算法对分接开关振动信号进行处理，能够获得比传统时频分析方法更为精细的时频特征表达，有效提升样本的特征维度，有利于实现分接开关运行工况的准确判定。

2）以多个MobileNetv2 轻量级CNN 作为基分类器，通过Adaboost 自适应提升机制对其进行强化学习训练，并按不同权重进行组合，可构造出性能更为优越的RLCNN。

3）实验结果表明，本文所提方法可自动实现分接开关多工况的准确辨识，与其他方法相比，识别准确率更高，稳定性更好，优势更为明显，具有一定的实际工程应用价值。

由于有载分接开关故障类型较多，在后续研究中将不断积累构建其典型多样性故障数据库，用于强化完善本文所提方法的识别能力，提高变压器有载分接开关的运行可靠性。