基于AFSA-BP神经网络的光伏功率预测方法

陈文进，朱 峰，张童彦，张 俊，张锋明，谢 栋，茹 伟，宋美雅，范 强

（1.国网浙江省电力有限公司，杭州 310007；2.国网浙江省电力有限公司绍兴供电公司，浙江 绍兴 312362；3.武汉大学 电气与自动化学院，武汉 430072）

0 引言

气候变化和能源安全是当前人类社会发展面临的两大严峻挑战，在化石能源枯竭和环境变化的大背景下，世界各国都在努力探索转变以往依赖化石能源的生产和消费模式［1-2］。随着碳达峰、碳中和等能源战略目标的提出，建设绿色电网、推动能源转型，大力发展和使用清洁的可再生能源已势在必行［3］。在众多新能源行业发展过程中，光伏发电因其技术成熟、对环境零污染、应用范围广等特点，成为了能源转型的关键［4］。随着光伏装机容量的不断增加，对光伏输出功率进行精确预测可以有效预防光伏接入后对电力系统的冲击，为光伏的有效消纳提供保障。

目前针对光伏功率预测的方法主要分为两类［5］。一类是以气象数据和实测功率数据为基础，结合光伏场站的地理位置等参数建立预测模型与算法。文献［6］提出对天气类型进行多特征分析和提取，利用一阶差分和因子分析法提取气象数据的有效特征；文献［7］运用互信息熵等相关性衡量指标，对影响光伏输出功率的气象因素进行定性和定量分析，挖掘气象波动特性和功率数据的匹配关系；文献［8］通过天气分型，结合因果算法筛选不同天气分型下的关键气象因素，最后根据不同天气类型划分，进行分类预测。另一类是直接根据光伏出力的历史数据进行预测，通过采用人工智能算法，结合历史数据建立输入变量和输出变量之间的映射关系，预测未来的光伏功率输出。这种方法对历史数据的质量要求较高，大多具有较高的预测精度和泛化能力，主要包含BP（反向传播）神经网络法［9］、极限学习机［10-11］、支持向量机［12-13］等。其中BP 神经网络具有非线性映射能力强、模型简单等优点，在光伏功率预测方面得到了广泛应用。文献［14］提出一种将光伏发电样本进行模糊聚类，再利用BP神经网络进行分段预测的方法；文献［15］通过相似变量选取相似日，利用动量法优化BP神经网络进行预测；文献［16］利用主成分分析法，建立基于特征提取的萤火虫算法优化的BP神经网络预测方法。以上方法均实现了较优的训练效果及预测精度。

本文考虑引入AFSA（人工鱼群算法），利用AFSA 优秀的内在并行计算能力和较快的寻优速度［17-18］，通过分析气象数据与光伏功率数据的相关性，建立基于AFSA优化BP神经网络的光伏功率预测模型。采用AFSA实现对BP神经网络权值和阈值的优化，有效提高BP神经网络的全局寻优能力，从而提高光伏输出功率的预测精度。

1 数据清洗

光伏场站及气象站测得的数据中，可能存在数据缺失、突变等问题，且气象数据中包含大量、多维与光伏发电无关的气象因素。使用低质量的数据进行模型训练将对预测结果的准确度产生较大影响，因此需对数据进行清洗。

1.1 数据异常值剔除

在光伏输出功率数据中，夜晚辐照度低，光伏输出功率为零。大量零值数据将影响预测模型的性能与精度，需识别光伏输出功率的零值数据并剔除。

光伏输出功率与气象数据都是通过数据采集设备采集得到的，获得的原始数据中可能存在异常数据，需对其进行识别剔除。

本文采用3σ准则对数据进行清洗。由于光伏输出功率与气象数据大致服从于均值为μ、标准差为σ的正态分布，由正态分布的特性可知，数值A分布在(μ-3σ，μ+3σ)内的概率为：

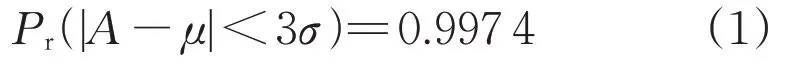
由于其概率极大，当数据值分布在(μ-3σ，μ+3σ)外时，可以将该数据视为异常值进行剔除。

1.2 气象因素相关性分析

光伏场站测得的气象数据包含气温、气压、相对湿度、辐照度等多种气象因素，且多种气象因素之间存在耦合关系，若考虑所有气象因素进行光伏功率预测，将大大降低预测精度，因此需对气象因素进行筛选，选取对光伏出力影响较大的气象因素。

对气象因素与光伏输出功率进行相关性分析，采用Pearson 相关系数r表征不同气象因素的相关性，计算公式为：

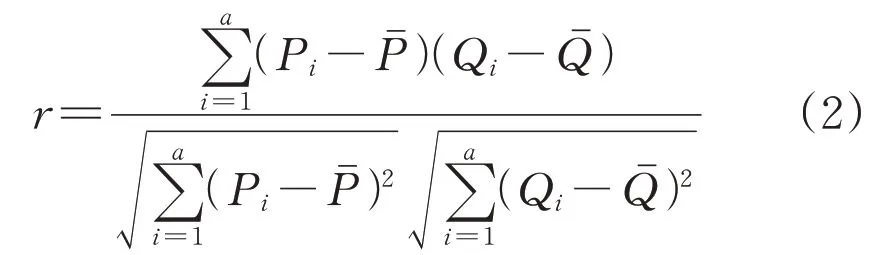
式中：a为数据样本数；Pi、Qi为数据样本；为样本平均值。

计算得到的气象因素与光伏输出功率的Pear⁃son相关系数值如表1所示。

由表1 可知，在光伏场站测得的各气象数据中，气温、总辐照度、法向直射辐照度、水平面散射辐照度与光伏输出功率呈正相关关系，气压、相对湿度与光伏输出功率呈负相关关系，且气压的相关程度最低。因此，在下文的仿真分析中，选取气温、总辐照度、法向直射辐照度、水平面散射辐照度这4个气象因素作为预测模型的输入变量，建立与光伏输出功率相关的预测模型。

表1 气象因素与光伏输出功率的Pearson相关系数

1.3 数据归一化处理

光伏输出功率与气象数据通常具有不同的数量级和单位，直接对其进行数据分析会影响预测模型的性能，需要对数据进行归一化处理。此外，不同数量级的数据将会影响神经网络的连接权值，导致神经元饱和，因此也需要对数据进行归一化处理，计算公式如式（3）所示。当预测模型训练和测试完成后，还需要对神经网络的输出值进行反归一化处理，才能得到真实预测结果，式（4）为反归一化的计算公式。

式中：pmax和pmin分别为原始序列的最大值和最小值；p为当前点的值；p*为归一化后的数值；t*为神经网络的输出值；t为反归一化后的数值。

2 基于AFSA-BP神经网络的预测模型

2.1 AFSA

AFSA 由李晓磊在2001 年提出［19］，通过描述鱼群的基本习性来模仿优化求解过程。假设人工鱼的数量为Nf，第i条人工鱼的状态向量为Xi=(xi1，xi2，…，xik，…，xiN)，其中xik为待寻优的控制变量，N为待寻优变量的个数。第i条人工鱼所在位置的食物浓度（目标函数）为Yi=f(Xi)。人工鱼之间的距离为dij=‖Xi-Xj‖，其最大感知距离为dvisual，移动的最大步长为S，鱼群拥挤度为δ。将预测模型的输出值与实际数值的RMSE（均方根误差）负值作为人工鱼的目标函数Yi，评价每次迭代中人工鱼位置的适应度值，即：

式中：eRMSE为RMSE 的值；M为预测模型输出样本数；和tb分别为预测模型输出值和真实值。

AFSA 主要包括觅食行为、聚群行为和追尾行为。

1）觅食行为。人工鱼在其感知范围内（dij≤dvisual）随机选择另一个状态Xj，如果得到的状态目标函数Yj较优，则向新状态移动一步。否则随机移动一步。用数学表达式表示为：

式中：k=1，2，…，N，xjk、xik、xi′k分别为状态向量Xj、状态向量Xi、下一步状态向量Xi′的第k个元素。

2）聚群行为。人工鱼通过探索感知范围内（dij≤dvisual）同伴的中心点状态Xc和中心点的目标函数Yc，计算公式为：

式中：nf为感知范围内的同伴数量；xck和xjk分别为中心点的状态向量Xc和第j个同伴状态向量Xj的第k个元素。

否则人工鱼执行觅食行为。

3）追尾行为。人工鱼探索感知范围内（dij≤dvisual）目标函数Y最优的同伴Xmax，若满足Ymax>δYi，表明同伴Xmax处目标函数较优且不太拥挤，则向同伴位置Xmax移动一步，即：

式中：xmaxk为状态向量Xmax的第k个元素。否则人工鱼执行觅食行为。

具体的参数设置如表2所示。

表2 AFSA参数设置

2.2 BP神经网络

BP神经网络于1986年由Rumelhart和McClel⁃land 首次提出，是一种利用梯度下降法按照误差逆向传播算法训练的多层前馈神经网络，是当前应用最为广泛的神经网络模型之一，其结构如图1所示。

图1 BP神经网络结构

BP神经网络具有非线性映射能力强、泛化能力强等优点，但同时存在学习速度慢、容易陷入局部最优等缺点，因此有待进一步研究。

本文采用的BP 神经网络仿真参数设置如表3所示。

表3 BP神经网络参数设置

2.3 AFSA-BP神经网络预测模型

本文利用AFSA 算法对BP 神经网络进行优化，以确定网络的最优权值和阈值，提高光伏输出功率的预测精度。AFSA-BP 预测模型的算法流程如图2所示，其具体步骤如下：

图2 AFSA-BP预测模型算法流程

1）对搜集数据进行清洗。首先根据3σ准则对数据进行异常值的识别与剔除；其次计算各气象因素与光伏输出功率之间的Pearson相关系数，选取影响光伏出力的主要气象因素；最后对数据进行归一化处理。

2）初始化BP 神经网络。构建BP 神经网络，确定输入层、输出层和隐含层节点个数，其中隐含层节点数s由式（10）确定，初始化BP 神经网络的权值和阈值。

式中：n和m分别为神经网络输入层和输出层的节点数；a为0～10的常数。

3）初始化人工鱼群。确立人工鱼群基本参数并初始化，将预测模型的输出值与实际数值的RMSE负值作为人工鱼的目标函数。

4）执行人工鱼群优化算法。人工鱼判断当前状态，执行觅食行为、聚群行为或追尾行为，从而更新BP神经网络权值和阈值。计算当前人工鱼目标函数值并与最优值进行对比，更新当前最优函数值。

5）判断退出迭代条件。将当前最优值与误差条件对比，若满足误差条件，则执行步骤6）；若不满足误差条件，则返回步骤4）。

6）训练BP神经网络预测模型。得到满足误差条件的最优权值和阈值，将其与训练数据集代入神经网络进行训练，得到预测模型。

7）预测结果输出。将测试集代入训练好的预测模型，对得到的预测结果进行反归一化处理，得到与原始数据量纲单位一致的数据，输出结果并计算相关评价指标。

3 仿真分析

为验证所提方法的优越性，本文采用2018 年某光伏电站10—12 月数据进行仿真分析，经清洗后的数据集包括每15 min采样的气温、总辐照度、法向直射辐照度、水平面散射辐照度数据以及对应的光伏场站输出功率数据。

图3为各气象数据与对应的光伏输出功率数据散点图。由图3可见，总辐照度与光伏输出功率相关性最大，法向直射辐照度次之，气温相关性最小，符合表1计算结果。

图3 气象与功率数据散点图

3.1 评价指标

在衡量预测模型的预测精度时，常用的评价指标包括RMSE、MAE（平均绝对误差）、MSE（均方误差）和MAPE（平均绝对百分比误差）。RMSE计算公式见式（5），其余指标计算公式如下：

式中：eMAE、eMSE、eMAPE分别为MAE、MSE、MAPE的值。

3.2 仿真结果

文献［20-22］中指出，运用GA（遗传算法）优化神经网络和PSO（粒子群优化）算法优化神经网络，相较于直接运用BP神经网络进行预测的结果更优，因此本文引入GA-BP 和PSO-BP 方法作为对照。将清洗后的数据集划分为训练集和测试集，其中前90%的数据作为训练集，剩下10%的数据作为测试集，分别利用仅BP神经网络、GABP、PSO-BP、AFSA-BP这4种方法进行建模预测，仿真软件为MATLAB R2020b。相关参数设置见表4和表5。图4为4种方法的预测结果。

表4 GA-BP参数设置

表5 PSO-BP参数设置

对4 种方法的预测结果分别计算RMSE、MAE、MSE、MAPE，见表6。

由图4、表6可知，GA-BP、PSO-BP 和AFSA-BP 方法在预测精度上相较于仅BP 神经网络均有提升，其中AFSA-BP 预测精度最高，与原始数据曲线拟合程度最优，相关误差评价指标最低。特别是在预测结果中段，可能由于云层遮挡、阵雨等天气原因，导致输出功率出现了大幅波动，AFSA-BP 方法仍有较优的预测效果。此外，PSO-BP比GA-BP具有更高的预测精度，与文献［21-22］中相关结论相符。

图4 4种方法预测结果

表6 4种方法误差对比

对4 种预测方法的训练耗时进行比较，结果见表7。可以看出，对BP 神经网络的权值和阈值进行优化明显增加了训练耗时。相较于GA 与PSO算法，利用AFSA对BP神经网络的权值和阈值进行优化，训练耗时较短。由此可见，使用AFSA优化BP神经网络的权值和阈值能有效提高光伏输出功率的预测精度，同时训练耗时较短，在光伏功率预测方面具有较高的优越性。

表7 4种方法训练耗时对比

4 结语

为提高光伏输出功率的预测精度，本文提出了一种基于AFSA-BP神经网络的功率预测方法，结果表明：

1）通过对所测数据的清洗及筛选，能有效降低气象数据的维度，提高数据质量，从而提高了计算速度，为后文模型的精度提升奠定基础。

2）与仅使用BP 神经网络、GA-BP、PSOBP 等方法相比，AFSA-BP 方法具有更高的预测精度，与原始数据曲线拟合程度更优，误差评价指标更低。

3）利用AFSA-BP 方法的模型训练耗时相对较短。

本文提出的优化模型在光伏输出功率预测方面具有一定的应用推广价值，有助于促进光伏的有效消纳，助力“双碳”目标的实现；同时，可在电力系统调度、储能等相关方面发挥作用，提高电力系统的稳定性。