非线性非平稳波浪极短期预测的复合优化模型

张茴栋， 张德康， 史宏达

(中国海洋大学 工程学院，山东 青岛 266100)

海上作业平台不仅受到风、流等多变量的影响，还主要受到波浪荷载的影响，具有非线性、非平稳性的海浪会加剧作业平台产生一种非稳态随机运动[1]。为了使平台保持稳定，许多深海平台装载了波浪补偿装置来抵消波浪作用。提升波浪补偿装置的准确性，需要对波浪运动趋势进行极短期预测，通过其预测结果提前对波浪补偿装置进行控制补偿。目前常用的波浪预测模型有自回归模型、自回归滑动平均模型等[2-3]。这些模型基本上都是线性模型，使用时需要被分析和预测的数据具有线性平稳性。为克服波浪时间序列中非线性因素对模型预测精度的不利影响，近年来多采用人工神经网络(artificial neural network，ANN)的方法对波浪有义波高进行预测[4-6]。其中，长短期记忆(long short-term memory, LSTM)神经网络能够通过深度学习充分利用时间序列中的相关性，实现对历史信息真实有效的利用[7]。此外，针对数据中非平稳因素对模型预测精度的不利影响，小波分解成为分析时间序列变化的周期性和趋势的有效技术之一[8-10]。但由于应用小波分解处理时间序列时需要预先设置固定的小波基函数，这种预设参数的方法限制了小波分解的有效应用范围。因此，有学者提出了对于非线性、非平稳时序具有较强自适应性的经验模态分解(empirical mode decomposition，EMD)的数据处理方法[11]。然而，EMD算法受到端点效应的影响，其分解质量会明显降低，进而影响模型预测的精度。极限波浪的序列具有明显的非线性和非平稳性，目前对其进行极短期预测的研究较为空缺。

根据预测模型的各自特性，本论文提出了一种组合预测模型：该模型首先采用镜像延拓(mirror symmetry extension，MSE)和LSTM算法联合消除端点效应，再运用EMD模型分解时序波浪(MLEMD)，最后依托LSTM神经网络预测时序分量并叠加重构预测结果，整个过程称为MLEMD-LSTM组合波浪预测算法。

1 EMD-LSTM组合模型

1.1 长短期记忆神经网络

LSTM是基于循环神经网络(recurrent neural networks，RNN)优化的一种算法[12]，其可以有效消除梯度消失情况的产生，并且能对时序信息进行长时间学习[13]。此外其能够将记忆单元载入循环神经网络隐含层的神经节点之中，实现对历史信息的记忆，并且通过增加3种门结构(遗忘门结构，输入门结构和输出门结构)实现对历史信息的运用[14]。

如图1所示，设定输入序列为(x1，x2，…，xi)时，隐含层的状态为(h1，h2，…，hi)，对应t时刻有：

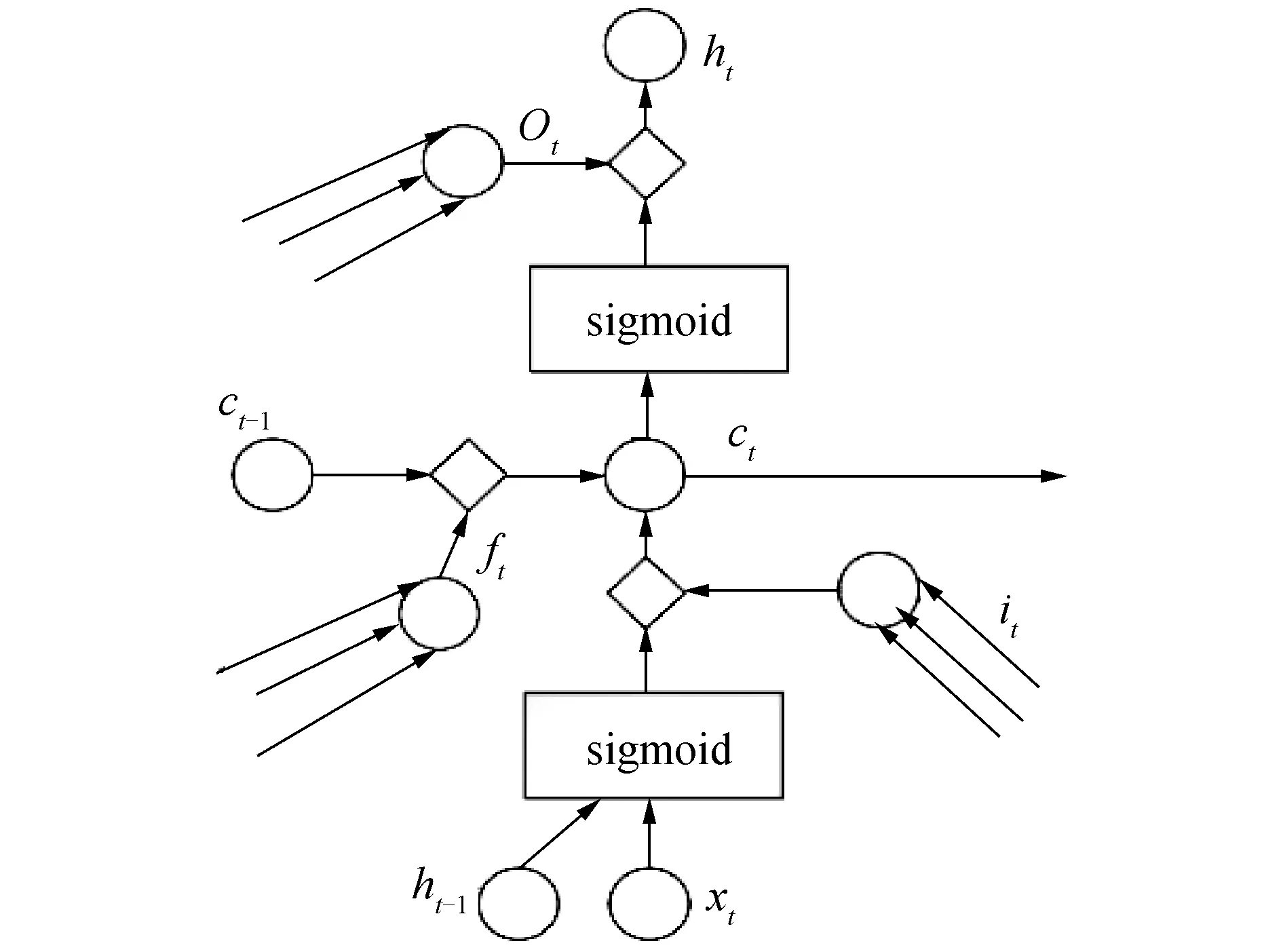
图1 长短期记忆神经网络结构示意

ft=sigmoid(whf*ht-1+wxf*xt)

(1)

it=sigmoid(whi*ht-1+wxi*xt)

(2)

ct=ft⊙ct-1+ic⊙tanh(wxc*xt+whc*ht-1)

(3)

ot=sigmoid(wxo*xt+who*ht-1+wco*ct)

(4)

ht=ot⊙tanh(ct)

(5)

式中：ft、it、ot分别代表遗忘门结构、输入门结构、输出门结构；ht-1是隐藏层单元在前一时刻的输出信息，ht代表实时LSTM单元输出；ct为LSTM记忆模块值；wh、wx、wc依次表示遗忘门、输入门和输出门位置的权重矩阵；sigmoid、tanh为2类激活函数。

1.2 EMD方法和EMD-LSTM模型

EMD是一种高效的时序分解算法，对于非线性、非平稳时序的处理具有较好的效果[11]。该算法将复杂的时间序列信号分解为有限个本征模函数IMF和一个残余项rn，其分解获得的IMF分量与分量rn具有原始时间序列在对应时间尺度上的全部波动信息[13]。

IMF具有2个特点:1)IMF函数局部最小值的包络线和局部最大值的包络线的平均值为0，即在时序的任意时刻，IMF的上下包络线都以时间轴局部对称；2)在时序的时长范围内，IMF的过零点数目和极值点数目必须相等或者至多相差为1。

具体的分解过程为：

1)设定原始时序的样本数据x(t)，运算求得该时序上的局部最大值和最小值，并分别进行3次样条插值，求得x(t)的上包络线xup(t)、下包络线xdown(t)序列，及上下包络序列的均值，从而获得包络线均值序列m1(t)：

(6)

2)将原始时间序列x(t)减去均值m1(t)，求得新序列h1(t)=x(t)-m1(t)，判断h1(t)是否满足IMF的2个特点：若满足，则h1(t)是提取出的一个IMF分量，此时用x1(t)=x(t)-h1(t) 代替第1步中的x(t)；若h1(t)不满足IMF这2个特点中的任意一个时，则用h1(t)代替第1步中的x(t)，重新分解，直到h1(t)满足IMF的特点；

3)重复以上分解步骤即可提取到下一个IMF分量，当xn(t)变成一个单调函数时分解停止，此时，已经无法再提取出新的IMF，最后一项xn(t)就是残余项rn[12]。

最终，相应的原始序列x(t)可通过n阶IMF分量和残差rn表示为：

(7)

式中：n为由x(t)决定本征模函数的个数；rn是分解的残余分量，是x(t)的主要趋势项；hi(t)为本征模函数[12]。

EMD-LSTM模型是一种非线性非平稳时间序列的组合预测模型[15]。其预测步骤为：1)将原始波高时间序列通过EMD分解为若干个IMF和rn残差；2)对分解后的每个分量分别采用LSTM模型进行预测；3)对每个预测结果进行叠加重构，得到最终的预测值。

2 复杂波浪的精准预测模型建立

在应用经验模态分解方法时，需要通过3次样条插值算法获得上、下包络线，时序的初始和末端位置由于受到端点的限制，缺少相应的极值点，导致插值点的不确定性和边界的严重失真[16]，使分解出的本征模态函数没有实际的物理意义。镜像对称延拓法是处理EMD端点效应的方法之一，如图2所示，该方法在数据边界处通过镜像对称延拓极值点，以满足EMD分解质量的需要[17]。然而，这种方法需要找到一个合适的端点进行延拓处理，在应用过程中，除了极少数端点(即图2的35 s处)的延拓结果表现较好，其余端点运用镜像对称延拓的结果并不令人满意，在延拓极值和实际极值之间总是存在显著差异，这使得该方法在预测模型中的应用存在很大弊端。

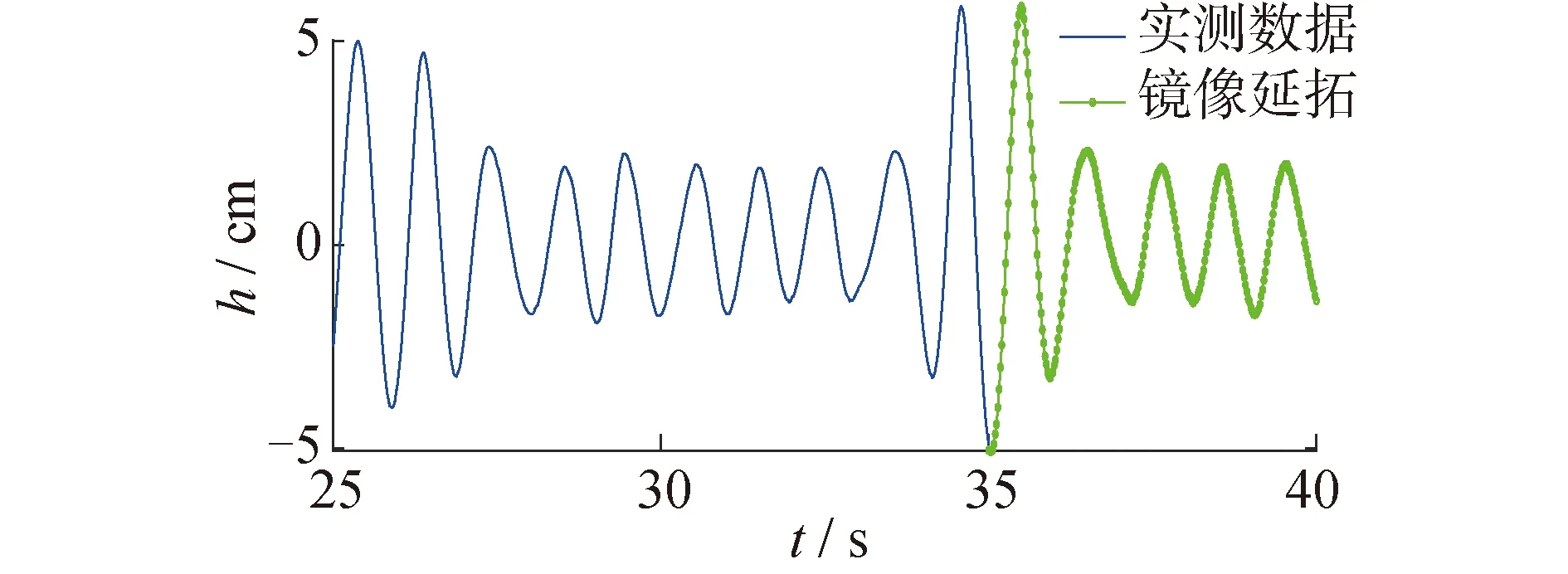
图2 镜像对称延拓

针对EMD端点效应严重影响其分解质量，以往延拓方法对端点效应改良不足，并且不能随时序变换而自适应延拓，本文提出了一种依托镜像对称延拓和LSTM算法联合处理端点效应，而后进行EMD分解的方法。如图3中步骤1所示，通过LSTM算法在原始序列的边界处拓展并识别出的第1个极值点，边界延展的长度一般不超过时序的半个平均周期，然后利用镜像对称延拓法从边界极值处延拓为一个对称且闭合的时间序列，这样既可以消除端点效应，又可以避免单独使用LSTM时导致误差增大的问题[17]。因此该MLEMD方法可以克服传统EMD的弊端，提高经验模态分解的精度。

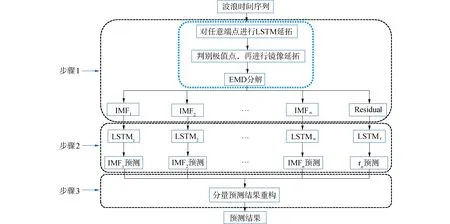
图3 MLEMD-LSTM模型预测流程

对于波浪时间序列的预测，需要通过训练数据构建时间序列内部关系，建立准确的预测模型，为后续时间序列预测提供可靠的依据。但是实际情况中波浪的绝大多数时间序列具有典型的非线性、非平稳性特征，针对这些复杂性较高的时间序列，若直接建立其预测模型，很难达到预测精度要求。本文提出的MLEMD-LSTM组合算法，首先使用镜像延拓和LSTM算法联合处理初始数据，然后采用经验模态分解处理非线性、非平稳性的波浪时间序列，降低时间序列的复杂程度，再运用LSTM算法分析复杂程度较低的IMF分量及Res残余项的变化趋势，最后通过序列叠加重构实现对复杂波浪的精准预测。

本文应用复合MLEMD-LSTM模型进行不规则波浪极短期预测的步骤为：

1)进行波浪时序分解，利用MLEMD分解算法，将波浪时序分解为n个频率由高到低分布的本征模态分量(imf1,imf2，…，imfn)和残差项rn；

2)建立全部imf分量及趋势项rn的LSTM预测模型，并对各个分量进行预测；

3)将各分量预测结果叠加重构得到最终预测值。

3 水槽试验及分析

3.1 水槽试验设置

为了验证MLEMD-LSTM组合模型对非线性、非平稳性波浪时间序列极短期预测的性能，以及进一步论证基于LSTM算法实现自适应镜像对称延拓进而消除EMD端点效应的可靠性，本文以中国海洋大学海洋动力水槽波浪试验中测得的一般不规则波、线性聚焦波以及非线性畸形波的自由液面时程曲线作为分析和预测的对象。水槽长度l=60 m，宽度b=3 m，实验时水深h=1 m。水槽内部布置15个浪高仪，采样频率为50 Hz，波高仪布置情况如图4所示。

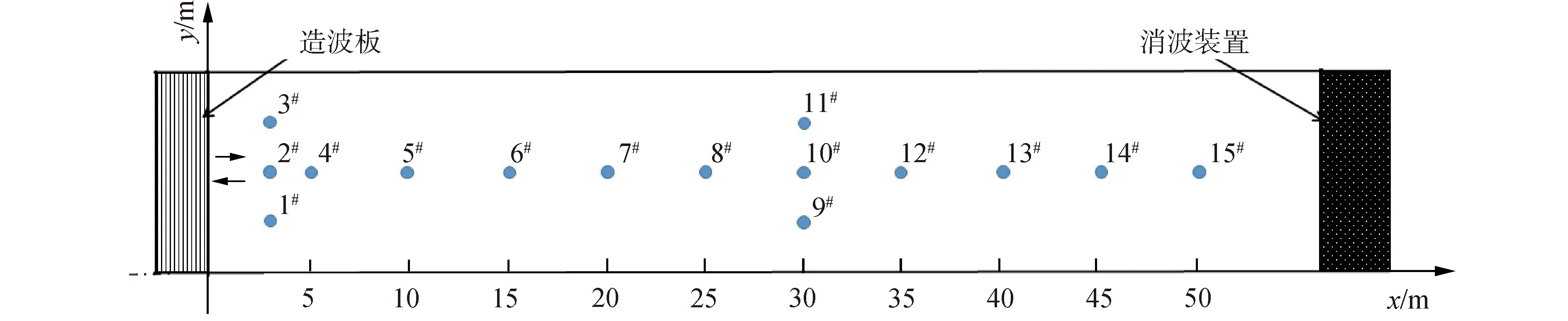
图4 水槽试验时波高仪布局示意图

由于波浪在水槽前端属于生成阶段，末端属于消波阶段，故而选取6#～13#波高仪所记录的波高历时数据进行预测分析，采样时间间隔为0.02 s，不规则波、聚焦波以及畸形波均设定有效数据点为3 000个，历时60 s。为简化展示内容，结果分析仅以10#波高仪所测数据作为典型代表。图5为10#波高仪所测得的3种波列时程曲线，其中训练样本与预测样本的时长分别设置为50 s、10 s，两者以50 s处虚线为分界线。

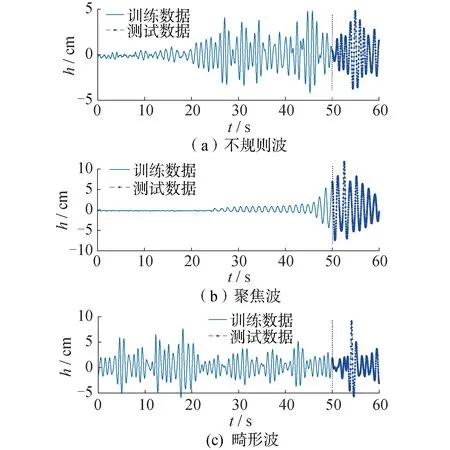
图5 波面时间序列及其数据划分

3.2 MLEMD分解及LSTM分量预测

在进行LSTM预测之前，运用MLEMD算法分解水槽试验获得的一般不规则波、线性聚焦波和非线性畸形波的训练样本序列，精准得到具有不同波动特征信息的本征模态分量。随着IMF的分解层数不断增加，对应IMF分量的波动频率不断下降，即低阶IMF分量代表时序的高频成分，Res代表时序的低频成分。其中不规则波分解所得本征模函数B1=(IMF1，IMF2，…，IMF6)和1个趋势项Res；聚焦波分解得到B2=(IMF1，IMF2，…，IMF5)以及趋势项Res；畸形波分解得到B3=(IMF1，IMF2，…，IMF7)及1个趋势项Res。图6以畸形波时序为例展示了MLEMD分解的效果(<50 s)以及LSTM预测的各分量的变化趋势(>50 s)。

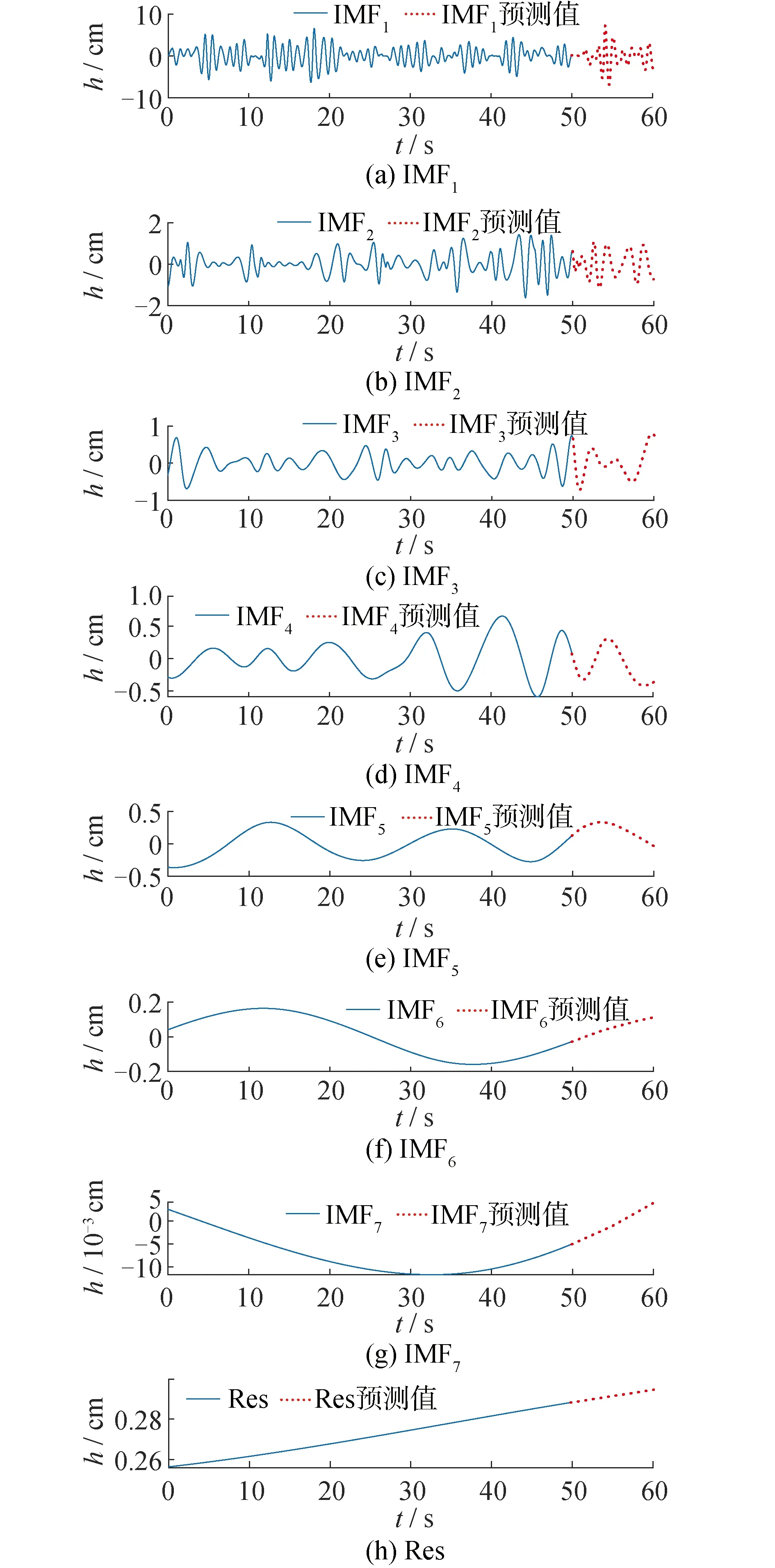
图6 畸形波时间序列的MLEMD分解及LSTM分量预测

3.3 预测结果与分析

本文采用均方根误差(root mean square error，RMSE)、平均绝对误差(mean absolute error，MAE)和纳什效率系数(nash sutcliffe efficiency，NSE)作为预测结果的评价指标：

(8)

(9)

(10)

为了清晰地表明MLEMD-LSTM组合模型对非线性、非平稳波浪时间序列的预测更具有优越性，本文同时对比了LSTM模型以及传统EMD-LSTM模型的预测效果，3个模型中LSTM的输入层层数、输出层层数、隐藏层层数均设定为1，隐藏层节点数设定为10，原始学习率设定为0.002 5，激活函数采用sigmoid和tanh函数[13]。LSTM的结构参数以及权值采用网格搜索来进行确定[13]。

图7～9为3种模型的预测结果图，表1～3为3种模型预测结果的RMSE、MAE和NSE评价指标值。

由图7～9可知，原始波浪的波面时间序列具有非线性及非平稳性，单一预测方法构建的预测模型对其预测表现较差。在对时间序列运用EMD算法进行分解之后，一定程度上可以降低时间序列的复杂程度，但由于EMD的端点效应影响，传统的EMD-LSTM相较于LSTM模型预测精度提升幅度较小，个别位置甚至不及单一LSTM模型预测的精度。同时，使用自适应镜像对称延拓算法优化处理后，MLEMD-LSTM模型预测结果更接近实际测量值，其结果比单一LSTM和传统EMD-LSTM模型均有明显提高，证明利用镜像延拓和LSTM算法联合消除EMD端点效应的方法是显著有效的。

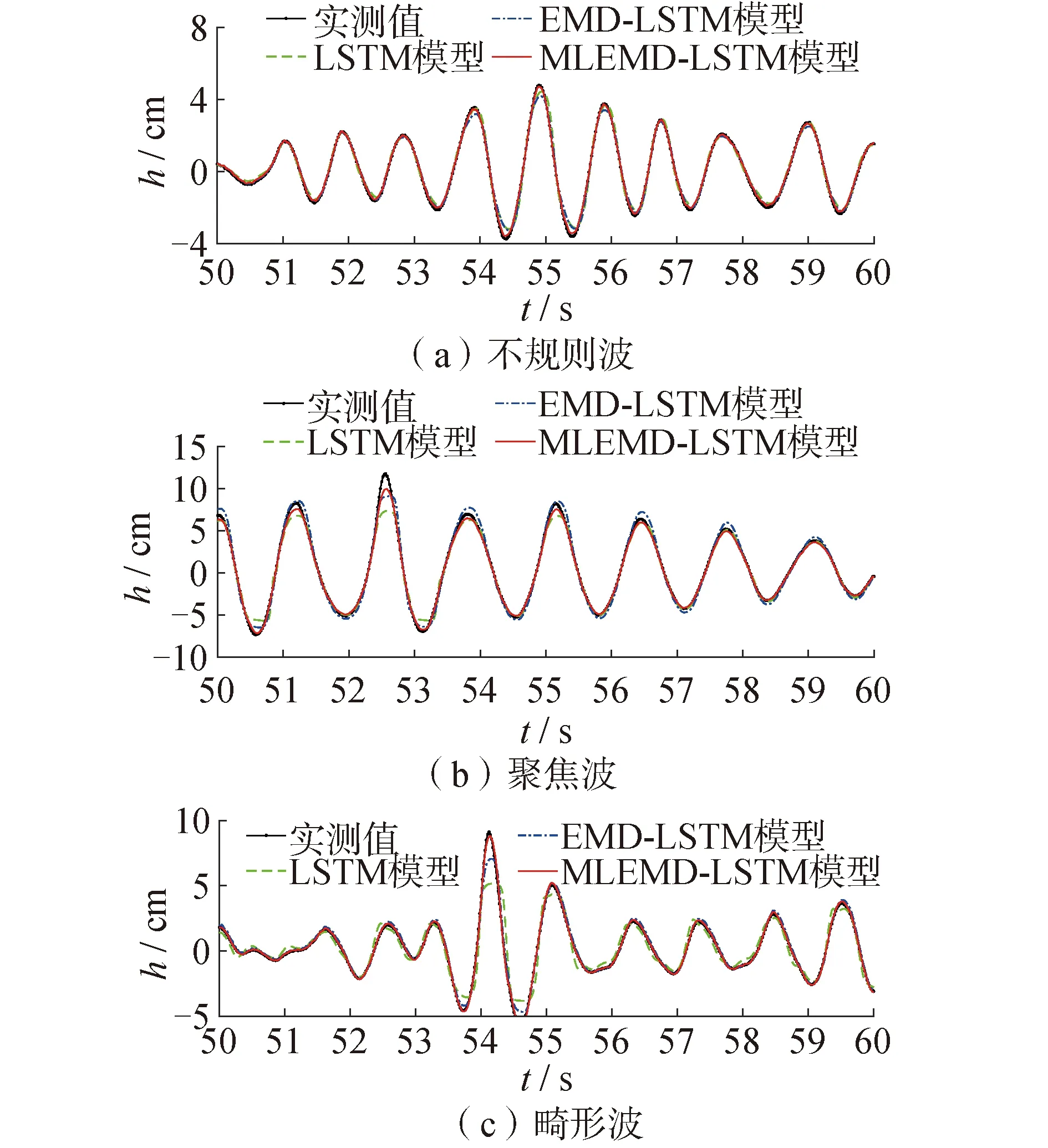
图7 预测结果对比

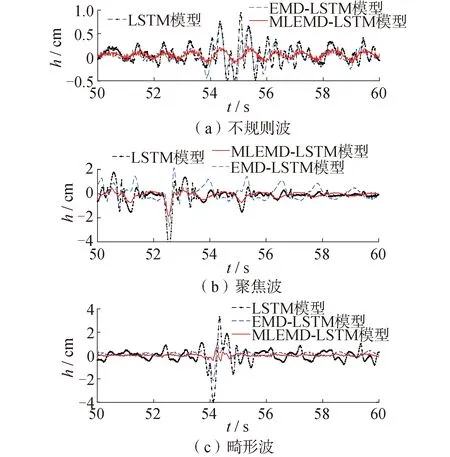
图8 预测误差对比

此外，表1～3的分析表明，MLEMD-LSTM组合模型相比于LSTM模型和传统EMD-LSTM模型：在对不规则波的预测中，预测结果的RMSE分别降低了62.4%和54.7%，MAE分别降低了57.7%和45.7%；在聚焦波的预测中，RMSE分别降低了56.4%和48.8%，MAE分别降低了50.4%和58.7%；在畸形波的预测中，RMSE分别降低了84.7%和65.7%，MAE分别降低了84.5%和64%。预测结果表明，MLEMD-LSTM模型对于不规则波浪的极短期预测是一种更加有效的方法。

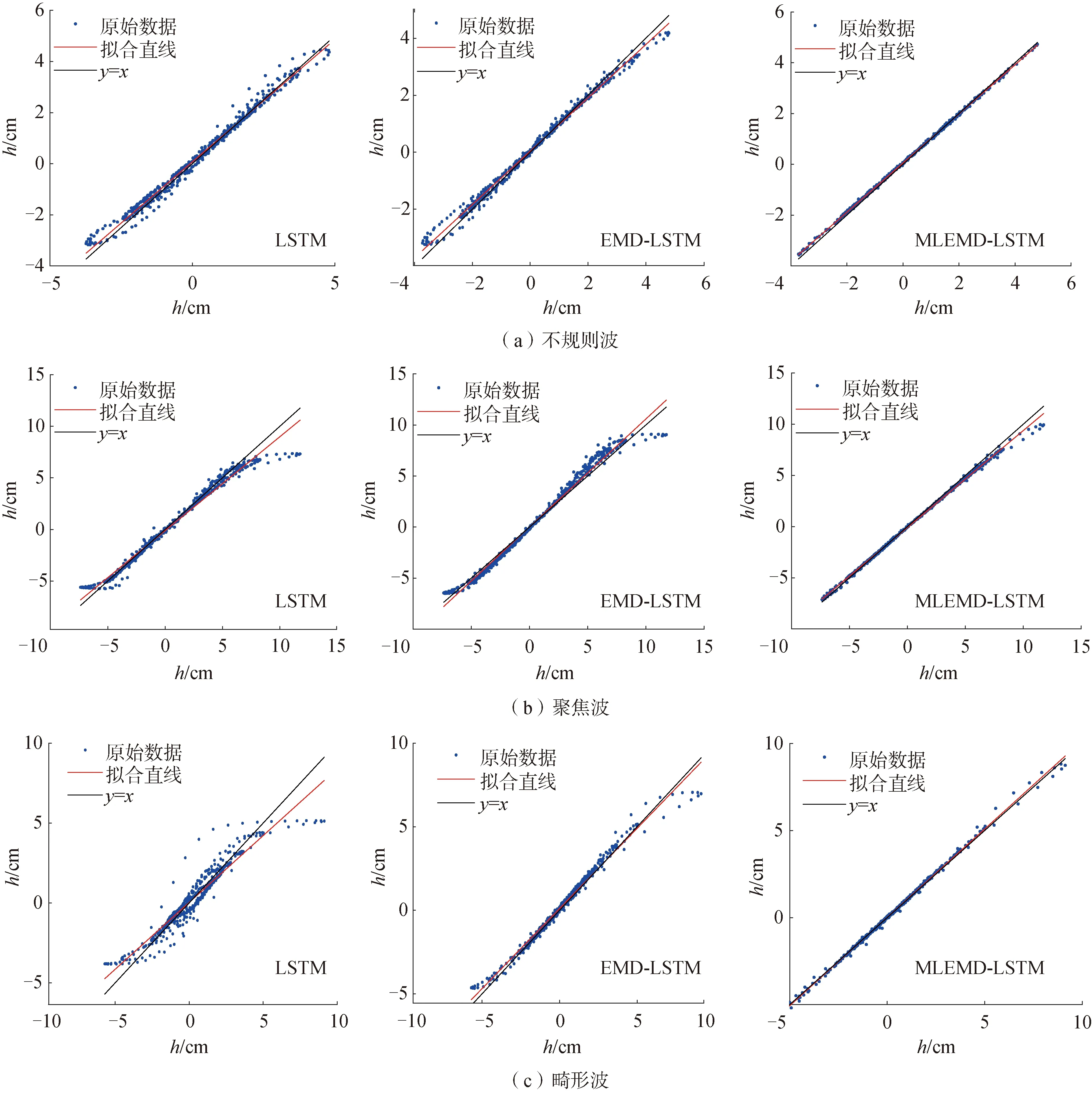
图9 预测结果拟合图

表1 不规则波预测误差统计结果

表2 聚焦波预测误差统计结果

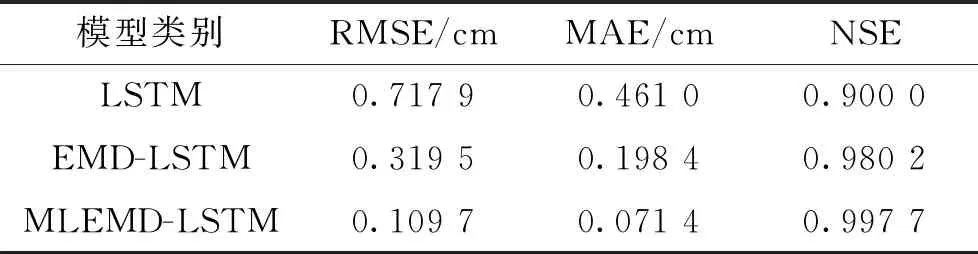
表3 畸形波预测误差统计结果

预测值与实际值的对比可知，3种模型所得预测结果与实际值的时间历程曲线大致相同，均能够表现出时序曲线的变化规律。MLEMD-LSTM组合模型的预测结果相比于其他2种模型，在RMSE及MAE上均为最小，在NSE上更接近于1，表明其预测效果比另外2种模型更加有效，对于非平稳、非线性的波浪时间序列具有更强的预测精度。

4 结论

1)在极短期不规则波浪时间序列预测应用中，MLEMD-LSTM组合模型相比于传统EMD-LSTM模型预测误差(RMSE、MAE)均降低45%以上，证明镜像延拓和LSTM算法联合处理样本序列可以更加有效地消除EMD的端点效应。

2)针对非线性、非平稳的3种典型波浪时间序列，采用MLEMD模态分解后运用机器学习中的LSTM模型预测各分量时序变化趋势，最后叠加重构得到的预测结果具有较高的预测精度。

在后续的研究中，为进一步提升MLEMD-LSTM组合模型的预测性能，将着重探索GA、PSO等参数寻优算法对机器学习模型中相关参数优化的方法，增强该模型对非线性非平稳波浪的极短期预测精度。