斜流角对半浸桨叶剖面入水的水动力特性分析
丁恩宝, 常晟铭,, 孙聪, 吴浩, 赵雷明
(1.中国船舶科学研究中心,江苏 无锡 214000;2.哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001)
随着近年来高性能船舶的航速越来越高,半浸桨以其在较高航速下有较高的效率、较小的附体阻力、良好的空化性能等优势,具有非常好的应用前景。对于半浸桨的敞水特性的研究,试验研究是其一直研究的主要手段。Olofsson[1]对四叶841-B半浸桨进行了模型试验,研究了斜流角对不同傅劳德数和空化数的螺旋桨特性的影响,得到的试验数据为后续的半浸桨的数值模拟的研究提供了大量的支持。近年来,随着计算流体力学技术的发展,研究人员大多采用CFD的方法对半浸桨的水动力和通气特性进行研究,文献[2-11]就杯型随边、斜流角等参数对半浸桨进行了数值模拟的研究,均得到了不错的结果,为半浸桨在实际工程中的应用提供了技术指导。
但由于半浸桨在工作时伴随着通气现象、自由液面提升等一系列复杂的水动力学机理,目前的数值模拟的精度难以满足现在的工程应用,因此从二维的角度研究半浸桨一方面能够直观地观察流场细节性的变化,另一方面又减小了计算量,从而可以得到大量的计算结果以便于进行机理分析,是一种对半浸桨研究的极佳思路。文献[12-13]通过计算流体力学的方法,对半浸桨二维剖面入水的水动力特性进行分析,验证了该方法能准确地预测二维剖面的受力情况和通气性能。半浸桨在工作的时候,由于其传动轴倾角会发生改变,进而影响其出入水过程中的斜流角的大小,因此斜流角的大小对半浸桨叶剖面入水过程水动力特性分析十分重要。
本文采用RANS方法,结合标准k-ε湍流模型、流体体积方法以及重叠网格技术,研究了不同斜流角的工况下的半浸桨无因次半径为0.7处的杯型剖面的入水过程的水动力特性、自由液面形式、通气腔形式、流场形式以及表面压力分布等,并在此基础上,对半浸桨杯型剖面入水过程中斜流角对其水动力特性的影响进行分析,并对相关机理进行研究。
1 物理条件设置
1.1 计算对象参数
本文选定得计算模型是841-B型螺旋桨的0.7R位置的杯型剖面,具体的半浸桨模型和0.7R对应位置的杯型剖面的形式如图1所示,R为桨模的半径。
对于841-B型半浸桨模型而言,其为图1(a)所示的四叶半浸桨,其直径为250 mm,毂径为85 mm,盘面比为0.58。在径向0.7R的位置上,叶剖面的弦长为119.45 mm。

图1 半浸桨的实桨和剖面模型
1.2 计算工况设置
1.2.1 水动力性能系数的确定
由于本文是采用半浸桨叶剖面进行机理研究,因此相对应的半浸桨的进数系数J、推力系数KT、扭矩系数KQ以及敞水效率η等需要以图2的方式进行的改变,具体的水动力性能系数为:

(1)

(2)
(3)
(4)
式中:VA表示进速;T为半浸桨产生的推力;Q为半浸桨吸收的扭矩;Fx为二维杯型剖面的x向受力;Fy为二维杯型剖面的y向受力;b为2.5D网格的z向计算域厚度;n为转速;D为直径;ρ为水的密度;U和V分别为进速和切向速度。
除了水动力参数的转化方式,图2同样显示了本文的半浸桨叶剖面斜流角变化的方式。

图2 半浸桨叶剖面入水的水动力性能参数的转换方式
1.2.2 计算工况的确定
基于之前半浸桨相关数值模拟的计算经验[8-9,13],本文选定的半浸桨杯型剖面的入水过程的进速系数确定为0.8≤J≤1.3,转速为2 254 r/min,在计算过程中,通过改变来流速度和杯型剖面垂向入水速度的大小来模拟试验的工况,具体的不同攻角情况下的工况设置如表1所示。

表1 半浸桨杯型剖面入水工况设置
1.3 网格模型的建立
1.3.1 边界条件的设置
本文在STAR-CCM+软件中采用一种垂向尺度较小,层数较少的2.5D网格进行建模,这种网格在进行数值模拟时一方面能够反映模型的三维尺度,另一方面网格较少能够保证足够的计算效率。具体的边界条件如图3所示,由于使用了重叠网格的方式模拟模型的运动,杯型剖面附近需建立一个计算域,该计算域的交界面边界设置为重叠网格交界面,杯型剖面设置为不可滑移壁面的边界形式。

图3 边界条件设置
1.3.2 网格模型设置
本文网格模型的背景域和重叠域部分为切割体网格,半浸桨杯型剖面表面附近为棱柱层网格,为了精准模拟半浸桨杯型剖面运动过程中的自由液面的变形以及流场的变化,需要对重叠网格区域、重叠网格运动域以及自由液面处的网格尺度进行加密,整体网格的划分如图4所示。

图4 网格划分形式
1.3.3 网格无关性验证
为了验证网格的收敛性,本文选取了Mesh1(634 501)、Mesh2(824 416)、Mesh3(1 085 275)3种形式的网格加密形式,并选取了0.7R处的半浸桨杯型剖面的0.8进速系数情况下的工况进行网格的收敛性分析,并提取了对应的入水过程时的垂向受力以及横向受力的时历曲线如图5所示。并综合计算精度和计算效率,选择的网格为网格数为824 416的Mesh2。

图5 网格无关性验证
1.4 数值模拟的验证
为了验证本文数值模拟的方式的可行性以及网格模型的精度,本文选取小底升角楔形体高速入水的工况进行数值模拟方法和半解析方法[14]之间的验证。其中,楔形体的入水速度为30 m/s,通过建立与1.3节相同的网格模型,监测如图6所示的A点和D点2点的压力值的时历曲线,并将数值模拟的结果与半解析方法、Oger[15]和Khayyer[16]的数值模拟方法进行比对,具体的比对结果如图7所示。

图6 小底升角楔形体模型参数和测点布置
图7的比对可以发现,现有的数值模拟方法在测得的压力的峰值抑或是压力值的演变规律等均能取得不错的结果。尤其在0.001 5 s之前,无论是压力值,还是压力值演变的趋势上,数值模拟的结果均与半解析解相差无几。但是随着时间的不断推进,由于半解析方法能够考虑到楔形体入水时的结构变形,进而影响流场中表面压力分布的求解,本文的模拟结果与半解析解的误差逐渐增大。但总体来看,所得较优于数值模拟方法。因此,本文采用的数值模拟方法的精度已经足够。
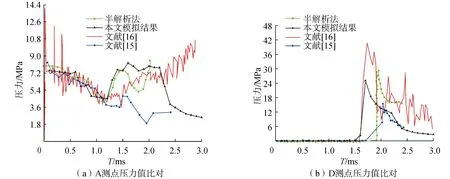
图7 楔形体不同测点抨击压力曲线
2 斜流角对叶剖面入水的性能分析
2.1 自由液面形式及通气形式的变化
为了探究斜流角对通气作用的影响,提取通气腔的长度和厚度,得到了不同斜流角工况下,通气腔的长度和厚度随进速系数的变化趋势,并如图8所示。而半浸桨杯型剖面入水过程中的自由液面的分布情况如图9所示。
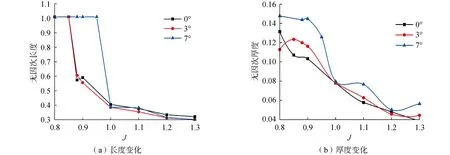
图8 不同斜流角下通气腔长度和厚度随进速系数的变化
通过图8可以发现,在3种斜流角对应工况下,通气腔的变化都是随着进速系数的不断增加,经过完全通气状态和部分通气状态的过渡,即随着进速系数的不断增加,在某一过渡状态时,原本覆盖剖面整个吸力面的通气腔的长度和厚度会大幅降低,并发生如图9所示的向随边方向收缩的过程,随着进速系数的进一步提高,通气腔的收缩程度趋于稳定,即长度和厚度在某一范围内轻微波动。由图9也可发现,相对于完全通气状态,部分通气状态下的自由液面的抬升程度会有一定程度减弱。
整体而言,不同的斜流角大小的半浸桨杯型剖面在入水过程中的自由面抬升高度并无比较大的区别。但是对于通气现象而言,增大杯型剖面的斜流角,会对通气现象有一定的促进作用。特别是如图9(b)所示,在没有斜流角以及3°斜流角的工况下,半浸桨杯型剖面的入水过程是部分通气的状态;但是当斜流角的大小达到7°后,通气状态则变为了完全通气状态。在完全通气的状态下,斜流角的大小主要影响了吸力面的导边附近以及随边附近的通气腔的厚度,并随着斜流角的增大,增大这些位置的通气腔的厚度,而对于吸力面的叶片中部附近,斜流角的大小并不会对通气腔的厚度有明显影响。但是斜流角的增大另一方面也增大了半浸桨杯型剖面入水过程的浸深,进而也会对通气腔的增大起到一定的抑制作用。这也就说明了图8所示的3°斜流角工况下的半浸桨杯型剖面的入水过程形成的通气腔的长度和厚度与斜流角不存在的时候几乎相同的原因。除此之外,随着进速系数的不断增加,尤其是达到了部分通气状态之后,斜流角对通气腔厚度的影响也会随之减弱,正如图9(c)所示,在进速系数达到了1.2时,整个气腔的分布并不会根据斜流角的不同而产生较大差异。

图9 不同进速系数下斜流角对自由液面形式的影响
2.2 敞水特性分析
为了进一步分析斜流角对半浸桨杯型剖面入水过程的敞水特性,本文将0°、3°、7°斜流角工况下的敞水曲线进行了比较,并如图10所示。

图10 不同斜流角下半浸桨杯型剖面入水过程敞水性能对比
通过比对图10所示的半浸桨杯型剖面的敞水性能,可以清晰地看出,这3组斜流角工况,Kx、Ky以及效率随进速系数的变化均会有相同的趋势,且最大敞水效率均发生在进速系数为1.2左右。
根据图10所示的横向受力曲线以及垂向受力的曲线可以发现,无论斜流角大小如何,Kx以及Ky的波动现象依旧会发生,而7°斜流角工况下的这个力的波动现象会较之另2种工况有所滞后。在斜流角的增大到7°的情况下,其通气现象会有较为显著的提升,并使得完全通气和部分通气之间的过渡状态下的进速系数有所滞后。
随着半浸桨杯型剖面的斜流角增大,其Kx以及Ky均会有所增大,这是因为在半浸桨杯型剖面的斜流角增大的过程中,其浸深会有一定程度的增加,进而会大幅度增加杯型剖面入水过程中受力的大小。此外,斜流角的增加另一方面也体现了该杯型剖面的攻角的增大,而攻角的增大一般会增大杯型剖面吸力面与压力面之间的流速的差值,进而增大吸力面与压力面之间的压力差,并反映到其横向及垂向的受力中。
尽管增大半浸桨杯型剖面入水过程中的斜流角会对其通气现象起到一个促进作用,但是根据图10(c)所示的结果,斜流角的增大并不能因为促进了通气现象就增大了其敞水效率,反而其敞水效率会随着斜流角的增大而有所降低。造成这种结果的原因是在每个斜流角下,半浸桨杯型剖面反映扭矩大小的垂向受力大小比半浸桨杯型剖面反映推力大小的横向受力大小增加得更多,且这种影响在斜流角越大时更为严重,因为杯型剖面的效率的最显著下降发生在斜流角为7°的情况下。
2.3 流场特性分析
当半浸桨杯型剖面入水过程中的斜流角发生改变的时候,一方面会改变入水过程时的流体的流动的方式;另一方面也能改变其通气腔的厚度,使得其流场的特性发生了改变。现将不同斜流角大小下的半浸桨杯型剖面的完全通气形式J=0.8、部分通气形式J=1.2以及过渡状态下的流场特性进行比对,并如图11~13所示。

图11 完全通气状态下不同斜流角的速度场
整体来看,在相同的进速系数条件下,随着斜流角的不断增大,半浸桨杯型剖面周围的流场的流速会有增大的趋势,而在半浸桨杯型剖面附近流速的分布形式则与斜流角的大小关系不大,即无论斜流角作何变化,吸力面附近的通气腔的流速均是非常大的;而导边附近的低速区以及随边附近的高速区也依旧是存在的。
随着半浸桨杯型剖面的斜流角的增大,完全通气状态下的吸力面处的空气高速流动的区域会由于通气腔厚度的增加而渐渐增大,并使得图13所示的不同斜流角的过渡阶段的进速系数随着斜流角的增长幅度有变大的趋势。而通过图11~13的观察,可以不难发现,随着半浸桨杯型剖面的斜流角的不断增大,其压力面的随边位置的高速区域的面积也会逐渐增大。
2.4 压力分布特性分析
为了更加清晰的观察不同斜流角情况下,半浸桨杯型剖面表面的压力分布的情况,提取了吸力面和压力面的压力分布随着导边到随边的分布情况,并如图14~16所示。
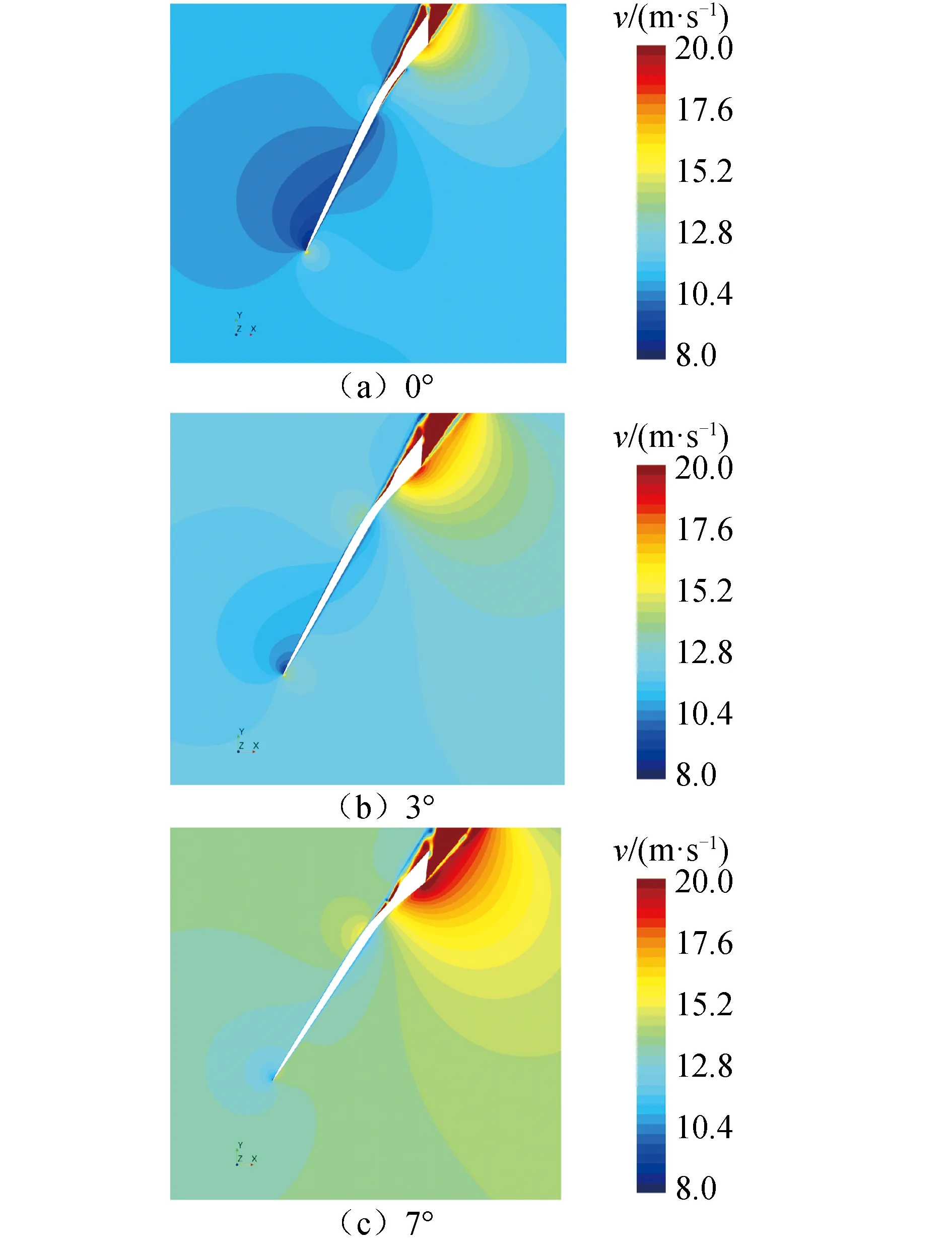
图12 部分通气状态下不同斜流角的速度场

图13 过渡状态下不同斜流角的速度场
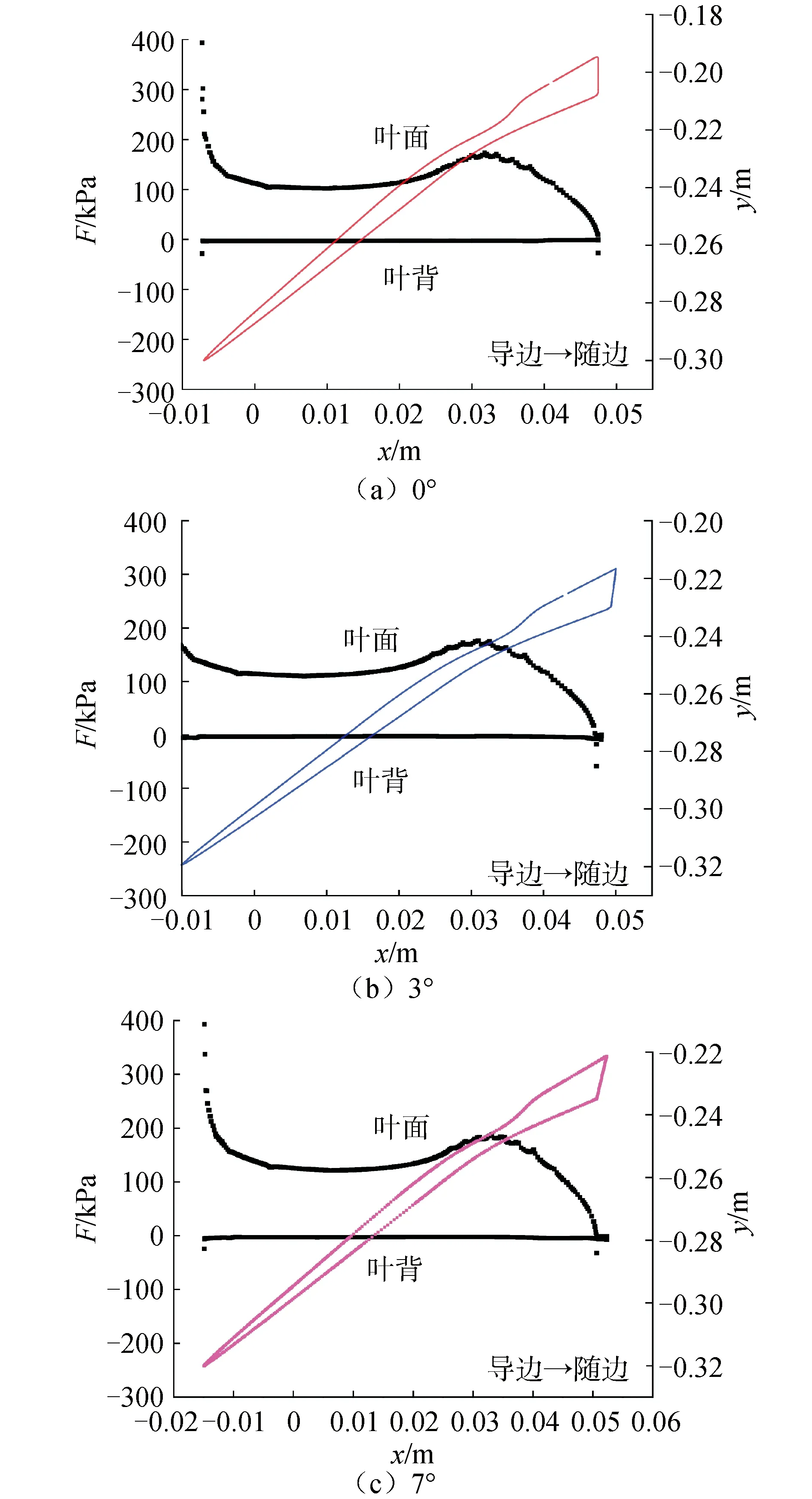
图14 完全通气状态下不同斜流角的压力场
对于图14所示的完全通气状态(J=0.8),由于半浸桨杯型剖面的吸力面上被通气腔完全覆盖,吸力面的压强则同大气压一致,因此无论斜流角的大小如何,半浸桨杯型剖面的吸力面上的压力分布几乎完全相同,且皆几乎等同于大气压的值。而关于杯型剖面的压力面,由于增大了半浸桨杯型剖面的斜流角相当于间接增大了压力面处的浸深,因此使得该部分的静压有所增大,进而使得吸力面与压力面之间的压力差有所增加,增大了半浸桨杯型剖面入水过程的横向以及垂向受力。
对于图15所示的部分通气状态(J=1.2),可见部分通气状态下,由于斜流角大小对流场的影响,会使得叶剖面的导边附近的压力差值和叶面的压力分布峰值发生明显改变。即随着斜流角大小的增大,半浸桨叶剖面吸力面与压力面之间的压力差明显增大,增大了半浸桨杯型剖面的横向受力以及垂向受力的大小。对于半浸桨杯型剖面入水过程的过渡状态,由于斜流角会影响入水过程中的气腔的形成过程,因此过渡状态发生时的进速系数和气腔状态也会随斜流角产生一定程度的变化。如图16所示,过渡状态下半浸桨杯型剖面的压力面处的压力分布由于流体的流动状态的相似性,分布趋势上并无较大差异;而吸力面处的压力分布则会因为气腔的分布以及收缩程度的不同而产生较大的差异。

图15 部分通气状态下不同斜流角的压力场

图16 过渡状态下不同斜流角的压力场
3 结论
1)随着半浸桨杯型剖面入水过程中斜流角大小的增加,半浸桨杯型剖面入水过程的自由面的抬升程度并不会有较大程度的改变,但是通气腔的长度和厚度都会随着斜流角的增大有所增加。除此之外,由于增大斜流角会在一定程度上增加浸深,而浸深的增大则是会对这个通气现象的加剧起到一定的抑制作用,其中3°斜流角工况下的抑制作用较为明显。
2)由于半浸桨杯型剖面的斜流角增大的过程中,其浸深会有一定程度的增加,因此其横向力系数和垂向力系数均会有所增大,但是由于斜流角增大的过程中,垂向力系数的增大程度要大于横向力系数,会使得半浸桨杯型剖面入水过程中的效率有所下降。
3)在改变半浸桨杯型剖面的斜流角的大小的时候,由于吸力面附近的流场变化较为剧烈,会影响其通气腔的生成。当斜流角增大到7°的时候,过渡状态对应的进速系数会明显增大。

