高弗劳德数通气超空泡流型迟滞特性数值仿真

罗凯， 左振浩， 许海雨， 刘富强， 叶常盛， 黄闯

(西北工业大学 航海学院，陕西 西安 710072)

超空泡航行器流体动力区别于全沾湿航行器，其流体动力取决于航行体与空泡流型的位置与运动耦合关系[1-2]，超空泡流型的精准预估对超空泡航行器的控制和稳定航行至关重要，而调控通气量是控制空泡流型的重要途径与方法[3-4]。超空泡航行器航行环境恶劣，当航行工况改变时，为了维持预期的空泡与航行体的位置耦合关系，需要时时调整通气量以维持空泡流型的稳定；但改变通气量时，空泡流型的变化可能比较缓慢，需要一定的响应时间才能稳定，由此造成空泡与航行体位置耦合关系的改变，进而影响超空泡的稳定航行。因此，研究变通气量时超空泡流型的变化特性具有十分重要的理论与工程价值。

近年来，国内外学者运用试验、数值模拟、理论计算等方法对通气超空化问题开展了大量研究。为了探究通气量对空泡泄气方式的影响，王科燕等[5]开展了扩张裙超空泡航行器的流体动力试验，得到了通气率对空泡尾部闭合流型的影响规律；Karn等[6]通过水洞试验观察到回射流泄气、双涡管泄气、四涡管泄气和波动超空泡泄气等9种超空泡泄气方式，并指出通气率对空泡泄气方式转换的影响通过改变泡内压力实现；周景军等[7]基于分相流模型建立了低弗劳德数通气超空泡定量研究数值方法，通过改变弗劳德数和通气率模拟了双涡管泄气和回射流泄气2种超空泡泄气方式；Lei等[8]采用欧拉多相流模型研究了通气率对双涡管泄气超空泡流型的影响特性，指出随着通气率的增大超空泡整体几何尺寸增大，并且2个中空涡管亦变粗。Wu等[9]采用PIV技术通过分析通气超空泡内气体流动结构及泄气模式，得到了通气率对回射流泄气超空泡形态的影响机理，指出通气率增大时，回射流通气超空泡需要整体几何尺寸增大以平衡从空泡内表面的泄气量。为了探究通气量变化对空泡形态的影响，王晓娟等[10]在高速水洞实验室进行了系列通气流量突降对空泡形态的实验研究，结果表明在某些通气流量范围内，通气流量突降会使空泡形态产生大的波动；Vlasenko等[11]通过系列水洞试验，获得停止通气后超空泡的非定常演化规律，并指出此规律受后体直径影响；张学伟等[12]根据Logvinovich空泡截面独立膨胀原理发展了一种用于计算非定常通气超空泡形态的计算方法，并运用该方法对通气超空泡形态稳定性进行了数值模拟研究，指出空泡长度和空泡数对通气率变化表现出时间滞后性。通气超空化问题的研究多集中在定通气量与稳定发展空泡形态的关系，而变通气量对超空泡形态动态变化特性的研究多集中于低速超空化流动且通气量变化规律单一，缺少变通气量对高速通气超空化流动的研究。

本文基于CFX平台，结合多相流模型、湍流模型和空化模型，构建定量求解通气超空化问题的数值模型，对通入非定量可压缩气体的高速航行器进行分析，研究通气量变化时超空泡特性尺度的动态演变特性，并基于空泡内压力的变化特性，揭示其作用机理。

1 数值方法构建及合理性验证

1.1 数值计算模型

通气超空化流动涉及到多相流、湍流等流体力学难点问题，随着计算流体力学的发展，已建立了多种可用于揭示超空化物理本质的多相流模型和湍流模型。相比较于均质平衡流模型，分相流模型在预测通气超空泡形态和空泡流动结构特性方面具有更高的计算精度，SST湍流模型可精确预测伴有逆压梯度的流动分离[7]，在通气超空泡的定量计算中有着较高的计算精度。因此本文采用分相流模型和SST湍流模型研究通气量变化时超空泡特征尺度的动态演变特性，此外考虑到计算中涉及的自然空化问题，本文采用了Rayleigh-Plesset空化模型。

1.1.1 控制方程

分相流模型的控制方程包括连续性方程、动量方程、能量方程及气体状态方程，本文中通入气体为常温空气，忽略了气液两相间的能量交换，因此忽略能量方程。

1)连续性方程：

(1)

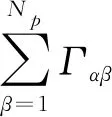
2)动量方程：

(2)

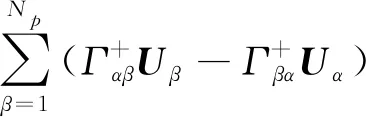
3)气体状态方程：

(3)

式中：ρair为气体密度；w为气体摩尔质量；pabs为气体绝对压力；R0为普适气体常量；T0为温度。

1.1.2 湍流模型

SST模型综合了近壁面k-ω模型的稳定性和边界层外部k-ε模型独立性的优点，方程中的系数是2种模型相应系数的线性组合。SST湍流模型的基本方程为：

(4)

(5)

式中：k为湍流动能；U为速度；μ为流体的粘性系数；μt为湍流粘度；pk为湍流生成率；ω为湍流频率；σω2、σω3、σk3、α3、β3和β′为模型常数。

其中：

(6)

(7)

式中：ν是运动粘度；y为到最近壁面的距离。

1.1.3 空化模型

本文采用Rayleigh-Plesset空化模型，该模型描述了液体中空泡的增长：

(8)

式中：RB为气泡半径；pv为气泡内压力；p为环境压力；S为表面张力系数；

若忽略二次项和表面张力项，式(8)可简化为：

(9)

则气泡体积变化率为：

(10)

气泡的质量变化率为：

(11)

假设单位体积内有NB个气泡，则体积分数可表示为：

(12)

则单位体积内总的质量运输率为：

(13)

上述公式是假设气泡增长即汽化时得到的，当气泡凝结时可得：

(14)

式中F为经验常数。

式(14)表征汽化时需要进一步修正，修正后方程为：

(15)

式中rnuc为成核位置点体积分数。

综合式(14)和(15)，可得凝结项和汽化项分别为：

(16)

(17)

式中RB=10-6m，rnuc=5×10-4，Fv=50，Fc=0.01。

1.2 计算模型

1.2.1 计算模型及边界条件

本文数值计算模型采用与俄罗斯“暴风雪”号相似的结构布局，模型包括空化器、通气孔、圆锥段、圆柱段、发动机尾喷管等结构，其几何模型示意如图1。

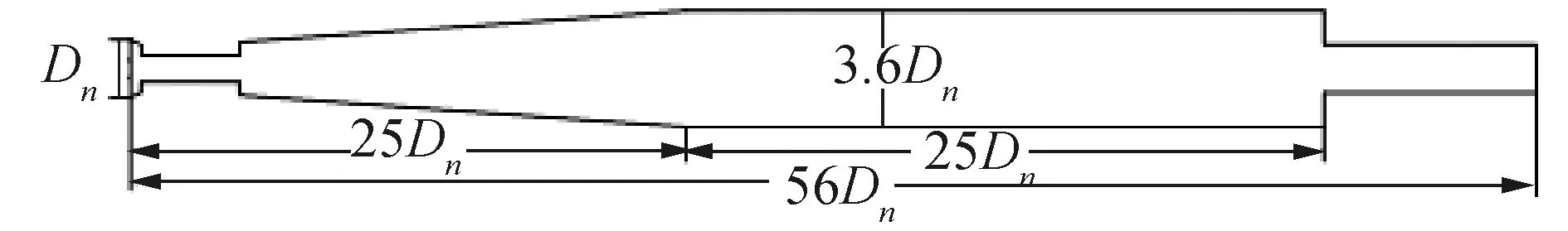
图1 超空泡航行器几何模型示意

当流域径向比大于54.0时，可忽略流域对通气超空泡尺度和压力分布特性的影响[13]，为消除流域的影响，本文采用的流域径向比为60.0。计算域左边界采用速度入口条件，速度大小为80 m/s，介质为纯液相；计算域右边界采用压力出口条件，压力大小为0.2 MPa，介质为纯液相；通气孔采用质量流量条件，具体数值由通气量变化规律确定，通气介质为可压缩空气；计算域外边界和航行器表面采用无滑移边界条件；具体结果如图2所示。

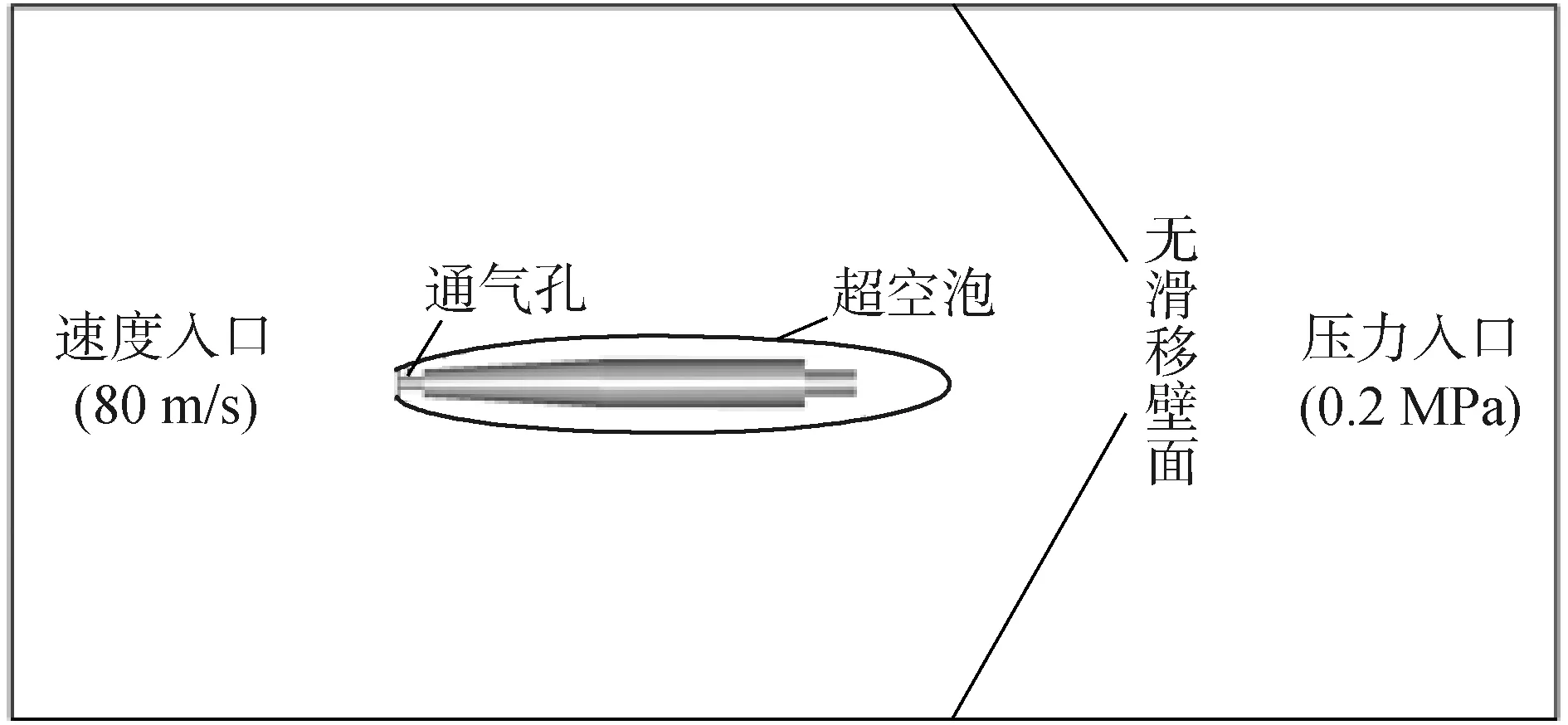
图2 计算域边界条件设置示意

1.2.2 网格划分

由于航行器和超空泡的对称性及航行器运动的对称性，进行网格划分时取计算域的一半以提高计算效率。由于通气超空化区域涉及剧烈湍流流动、气/水两相掺混作用，为了提高模型计算精度，对空泡生成区域进行网格加密处理。采用网格划分软件ICEM对计算模型进行网格划分，其中60%以上的网格集中在空化区，在对网格无关性进行验证之后，综合考虑计算机资源和计算精度，最终选取的网格数量约120万。航行器周围及空化器区域网格局部放大图如图3。

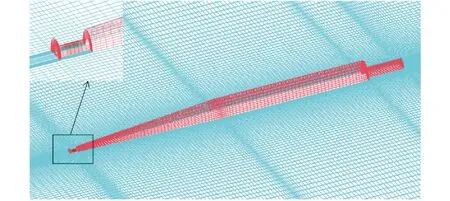
图3 航行器周围网格分布情况

1.3 数值模型验证

为验证数值模型计算通气超空化的精度，在西北工业大学高速水洞实验室开展系列通气率通气超空化水洞试验，从空泡泄气方式和空泡尺度等角度对计算精度进行评估，为了减小试验模型对通气超空泡形态的影响，试验模型采用细直杆模型。

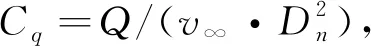
图4 数值仿真与水洞实验对比

为了进一步验证数值模型的计算精度，采用经验公式对通气超空泡进行定量验证。Logvinovich通过量纲分析和试验研究，建立了高Fr下通气超空泡通气率和空化数之间的半经验公式为：

(18)

式中：γ为经验系数，本文取0.15；σv为自然空化数；Cx0为空化数为0时的阻力系数；σc为通气空化数。

数值模拟结果同经验公式对比如图5所示。在相同空化数下，数值计算得到的通气率与经验公式计算结果的最大偏差小于3%，进一步证明了数值模型在模拟通气超空化流动时具有较高的计算精度。

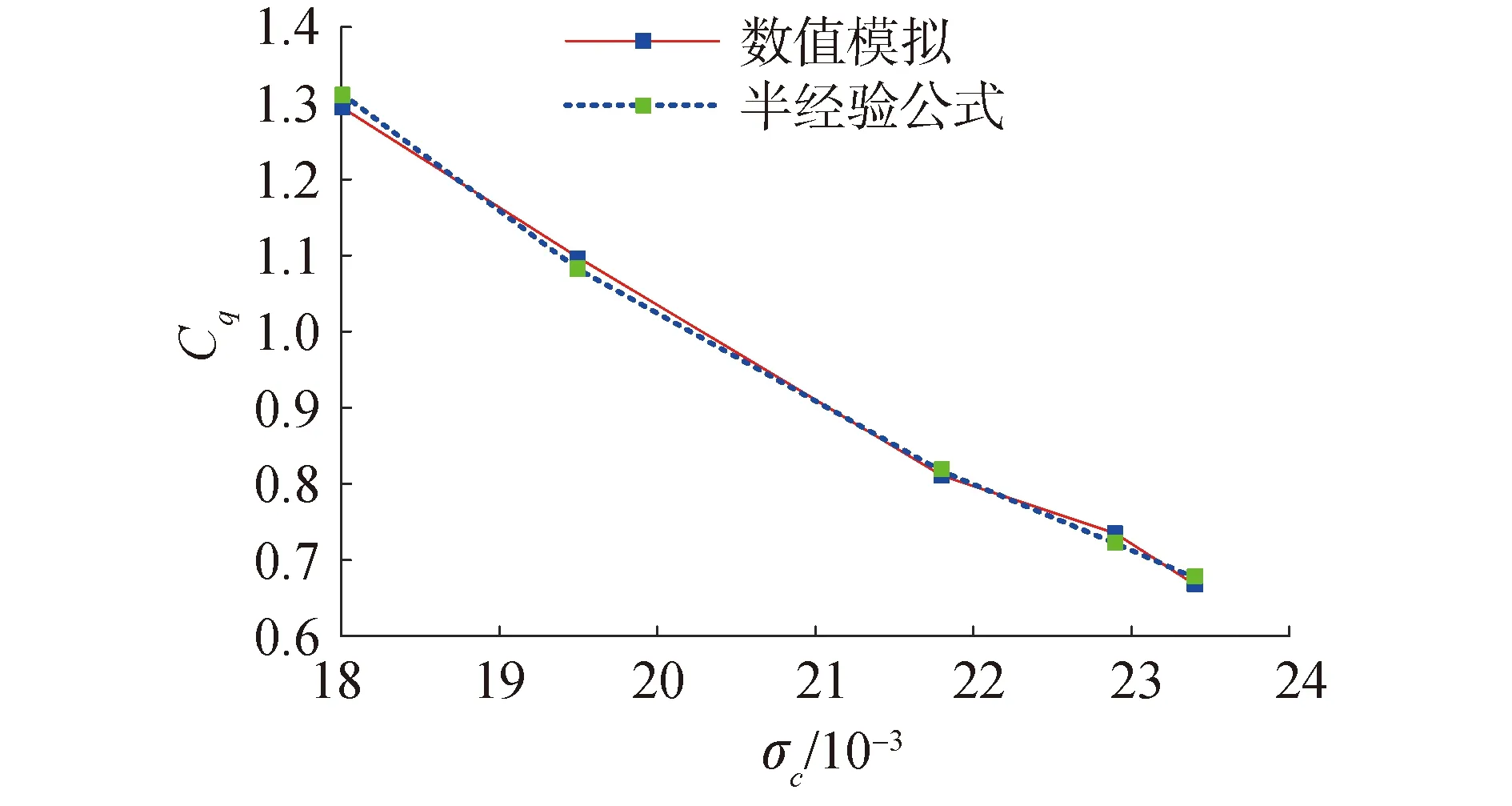
图5 Cq随σc变化规律

2 数值模拟结果分析讨论

为研究变通气率对通气超空泡流型的影响特性，本文定义了3种通气率变化模式，即通气率突增、通气率突降和通气率周期性变化。基于商用计算流体力学软件CFX 18.0平台，通过CEL语言实现了3种通气率分别随时间变化规律的编写，获得了弗劳德数为202时，不同通气率变化条件下空泡特征尺度(空泡最大半径、空泡半长和长细比)的变化特性，并通过分析通气超空泡泡内压力的变化特性，揭示在通气率变化时通气超空泡流型呈现时间迟滞特性的作用机理。

2.1 通气率突增

本文在Cq=0.45对应稳定超空泡流型的基础上，将Cq从0.45突增至0.60，以研究在通气率突增时通气超空泡特征尺度和空泡内压力的变化特性。

在通气率Cq突增变化条件下，通气超空泡特征尺度(空泡半长LDc和空泡最大截面半径Rmax)随时间的变化特性如图6所示，图中虚线表示通气率Cq=0.60时超空泡发展稳定所对应的空泡特征尺度。结果显示在通气率突增时，空泡半长LDc及空泡最大半径Rmax均未按照通气率变化规律发展，即空泡特征尺度未突增至通气率Cq=0.60所对应的稳定空泡特性尺度，而是在通气率突增后的初始阶段，空泡特征尺度增长迅速，随着空泡特征尺度逐渐接近通气率Cq=0.60所对应的稳定空泡特征尺度，其增长速度逐渐变慢。在本文计算工况下，通气超空泡特征尺度需要经过1.3 s后才能达到新的稳定状态，这表明在通气率突增变化时超空泡特征尺度表现出强烈的时间迟滞特性，空泡在达到新的稳定状态后，其特征尺度同通气率Cq=0.60对应的空泡特征尺度相同。

图6 通气率突增对空泡特征尺度的影响

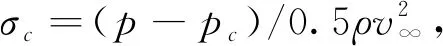
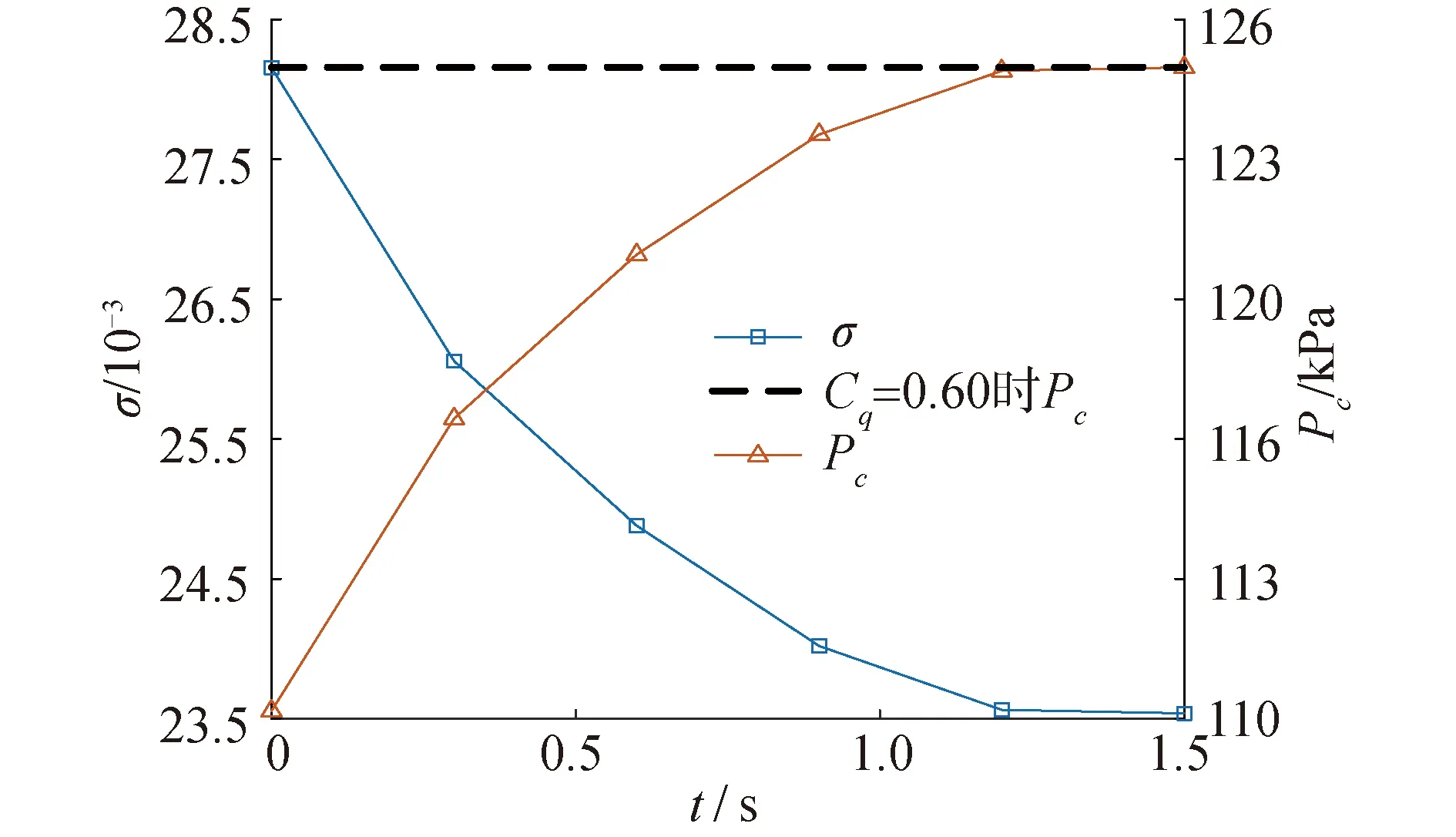
图7 突增通气量时空泡内压力和空化数的变化特性

2.2 通气率突降

本文在通气率Cq=0.60对应的稳定超空泡流型基础上，将Cq从0.60突降至0.45，以研究通气率突降时空泡特征尺度和空泡内压力的变化特性。图8给出了通气率Cq突降时超空泡特征尺度随时间的变化特性。通气率突降时，空泡特征尺度并未发生突降，而是在通气率突降后的初始阶段，空泡特征尺度减少迅速，随空泡特征尺度逐渐接近通气率Cq=0.45所对应的稳定尺度，其减少速度逐渐变慢。在本文计算工况下，通气超空泡特征尺度需要经过2.3 s后才能达到新的稳定状态，耗时约为通气率突增时的1.77倍，这表明在通气率突降变化时，超空泡特征尺度表现出更加强烈的时间迟滞特性。空泡在达到新的稳定状态后，其特征尺度大于Cq=0.45时对应的空泡特征尺度，表现出空泡特征尺度同通气率之间的迟滞特性，对于通气超空泡。当通气率降低时，超空泡形态减小有限[15]，本文研究结果与文献[15]相符，也再一次证明数值方法的可靠性。

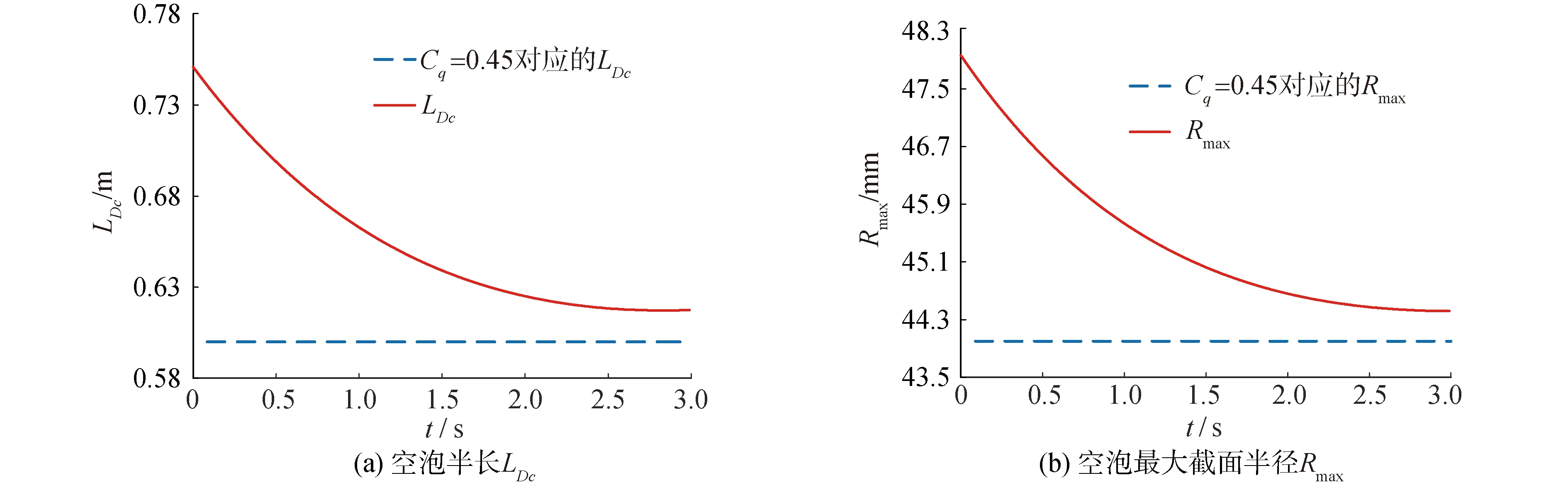
图8 通气率突降对空泡特征尺度的影响

图9表示了通气率突降时，泡内压力和空化数的变化特性。结果显示，通气率突降时，泡内压力不能发生突变，约需2.3 s才能达到通气率Cq=0.45所对应的稳定空泡泡内压力，耗时约为通气率突增时的1.77倍，因此通气率突降时空泡内压力具有更加强烈的时间迟滞特性，进而导致空泡特征尺度呈现出更加强烈的时间迟滞特性。此外，通气率突降后，获得的稳定空泡的泡内压力大于通气率Cq=0.45对应稳定空泡的泡内压力，这也就导致了通气率突降后获得的稳定空泡特征尺度大于通气率Cq=0.45对应稳定空泡的特征尺度。

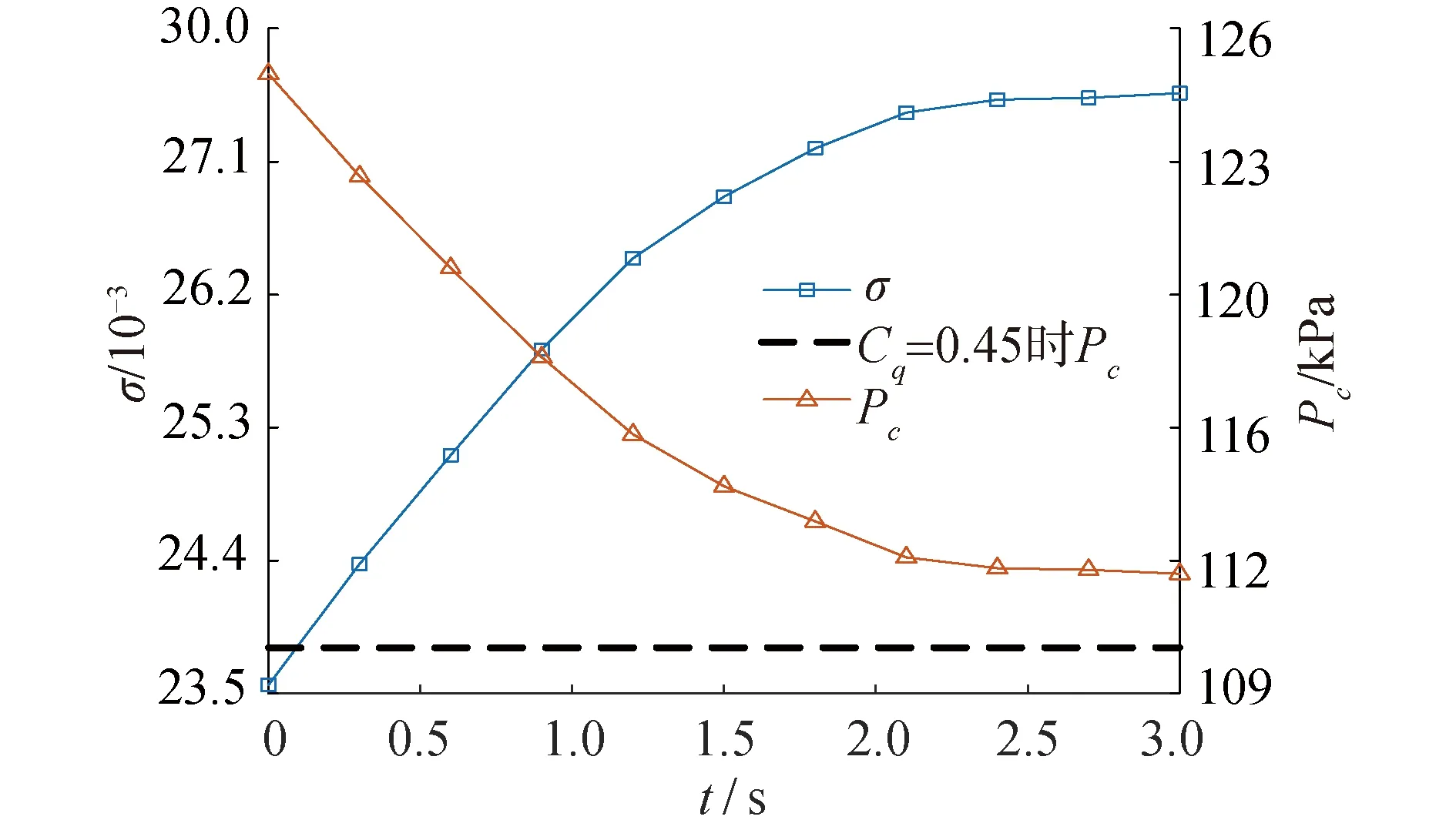
图9 突降通气量时空泡内压力和空化数的变化特性

2.3 通气率周期性变化

本文通气率以3种方波形式周期性变化，研究通气率以突增及突降周期性连续变化时超空泡特征尺度的响应特性。

2.3.1 通气率变化周期T=0.3 s

本文在Cq=0.45对应的稳定空泡基础上，将Cq突增至0.60，并保持0.15 s不变(此时空泡未充分发展)，然后将Cq突降至0.45，并保持0.15 s，此后通气率以此规律周期性变化，以研究此规律下空泡特征尺度的变化特性。

通气率以T=0.3 s的方波形式周期性变化时，初始4个周期内空泡特征尺度(空泡半长LDc和空泡最大截面半径Rmax)随时间的变化特性如图10所示。由图可知，两者的变化趋势相同，均存在时间迟滞特性，且此时都不是随着通气率变化而周期性变化。定义通气率突增后的半个周期内，空泡特征尺度增加量为Δ↑，通气率突降后的半个周期内，空泡特征尺度减少量为Δ↓，具体如图10(a)所示。在通气率的各个变化周期内，通气率突降引起的空泡特征尺度减少量Δ↓小于通气量突增引起的空泡特征尺度增加量Δ↑，随着时间的发展，每个周期内的Δ↓逐渐增大，而Δ↑逐渐减小，Δ↓/Δ↑逐渐增大，但空泡特征尺度总体呈增长趋势。以空泡半长LDc的变化特性为例，在第1个周期内，Δ↓/Δ↑约为0.16，第4个周期内，Δ↓/Δ↑约为0.70，增长了约338%。

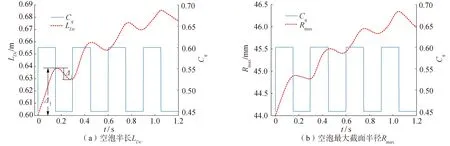
图10 通气率周期性变化(T=0.3 s)对空泡特征尺度的影响

2.3.2 通气率变化周期T=0.6 s

为了研究通气率变化周期对空泡特征尺寸的影响特性，本文将通气率变化周期增至0.6 s，以研究超空泡的形态变化特性。空泡特征尺度变化特性如图11所示。结果显示，两者的变化趋势与周期T=0.3 s时类似，都存在时间迟滞效应，且Δ↑、Δ↓、Δ↓/Δ↑的变化趋势相同。以空泡半长LDc的变化特性为例，在第1个周期内，Δ↓/Δ↑约为0.31，第4个周期内，Δ↓/Δ↑约为0.76，增长了约145%。无论周期T=0.3 s还是T=0.6 s，在第1周期内，通气率突增至0.60，空泡特征尺度未发展到Cq=0.60所对应的稳定空泡特征尺度，此时空泡具有继续发展的趋势，当通气率突降至0.45时，受空泡原有继续发展趋势的影响，导致超空泡特征尺度减小量Δ↓较小。在第2个周期初始时刻，通气率突增至0.60时，受空泡原有下降趋势的影响，相比较于第1个周期，第2周期内的空泡尺度增长量Δ↑减小；当第2周期内通气率突降至0.45时，空泡原有增长趋势要比第1个周期内通气率突降时弱，因此在通气率突降后空泡特征尺度的减小量Δ↓增加。此后的时间内，空泡特征尺度按照此规律发展。总结而言，在某一时刻tn时通气率改变所引起的空泡特征尺度变化特性是由该时刻tn前空泡原有发展趋势同通气率改变后引起的空泡发展趋势共同作用的结果。空泡发展趋势的强弱同空泡特征尺度同通气率0.45、0.60对应稳定空泡特征尺度的接近程度有关，空泡特征尺度对通气率突增响应变弱是由其逐渐接近通气率0.60所对应的稳定空泡所导致的。同理，空泡特征尺度对通气率突降的响应加强是由其远离通气率0.45所对应的稳定空泡特征尺度所形成的。

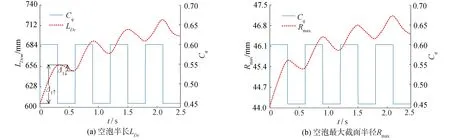
图11 通气率周期性变化(T=0.6 s)对空泡特征尺度的影响

2.3.3 通气率变化周期T=1.2 s

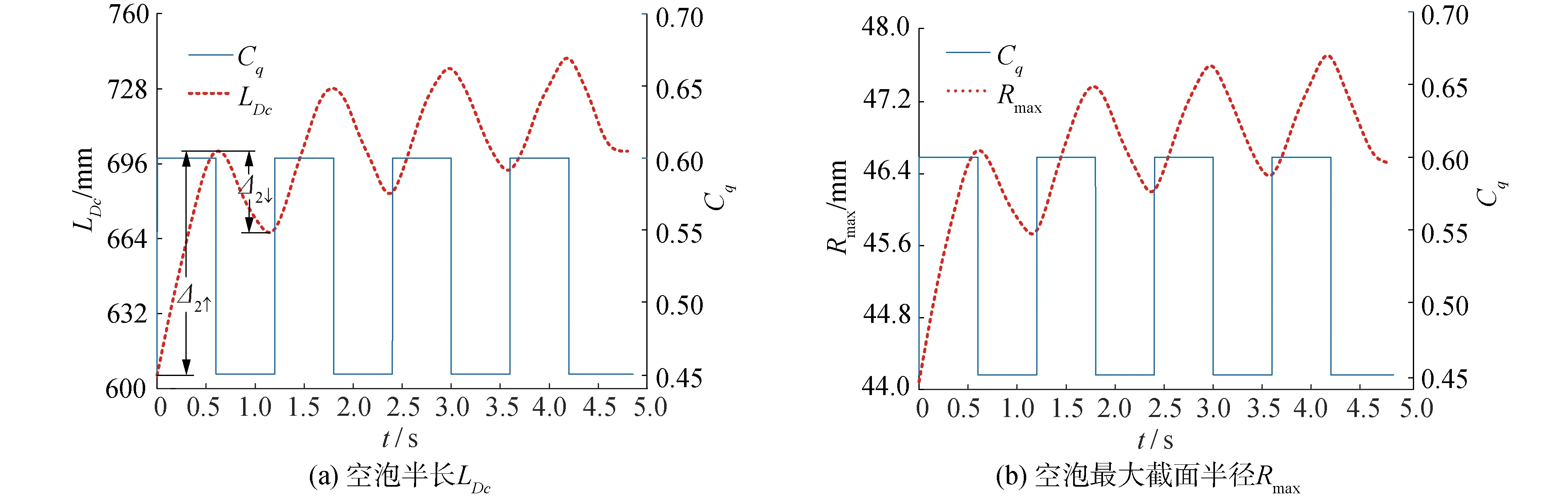
图12 通气率周期性变化(T=1.2 s)对空泡特征尺度的影响

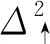
3 结论

1)通气量变化时，无论超空泡是否处于充分发展状态，空泡特征尺度变化存在时间迟滞特性。

2)空泡特征尺度体现出的时间迟滞特性强弱同通气规律有关。在本文中，通气量突增时空泡经1.3 s达到新的稳定状态，时间迟滞特性较弱，通气量突降时经2.3 s达到新的稳定状态，是突增时的1.77倍，时间迟滞特性较强。

3)通气量周期性变化时，空泡特征尺度初始变化不具周期性，空泡特征尺度增加量Δ↑逐渐减小，空泡特征尺度减少量Δ↓逐渐增大，Δ↓/Δ↑逐渐增大，最后趋近于1。空泡特征尺度变化特性是空泡原有发展趋势同改变通气率后空泡发展趋势共同作用的结果。

本文的未尽之处在于只研究了5种通气量变化规律下的空泡发展状况，没有对更多的通气量变化规律进行研究，并且研究通气量周期性变化时，只对初始发展的4个周期进行了研究。在后续工作中，将对多种通气量变化规律、更多周期数进行研究，获得一套变通气量时超空泡流型的预报方法，服务于超空泡航行器的工程实践。