火星大气高温光谱建模与非平衡辐射热流预测

吕俊明，李飞，李齐，程晓丽

1.中国航天空气动力技术研究院，北京 100074 2.中国航天科技集团有限公司 航天飞行器气动热防护实验室，北京 100074 3.中国科学院 力学研究所 高温气体动力学国家重点实验室，北京 100190 4.北京空间飞行器总体设计部，北京 100094

火星是距离地球最近的行星，也是太阳系中被探测最频繁的行星。以往的火星登陆任务中，失败多发生在进入-下降-着陆(Entry-Descent-Landing，EDL)过程，所以这个过程常被称为“死亡7分钟”，是关系任务成败的关键因素。近年来，随着火星登陆成功率提升，对火星大气环境的了解不断增加，对EDL过程、尤其是进入阶段的气体动力学和气动热力学预测能力随之不断提高，各种预测模型和方法也得到了验证。Wright等对火星进入气动热力学模型的发展和应用进行了综述，指出与对流加热和表面催化模型相比，高速进入引起的激波层高温气体辐射加热对于未来的火星探索任务可能非常重要。Johnston等的研究也表明，辐射加热是火星进入热防护设计中不确定性的主要来源之一。随后，火星科学实验室(Mars Science Laboratory，MSL)成功登陆火星，其飞行重建数据证明了这一点，同时证明火星进入辐射加热预测存在较大不确定性。

随着物理模型、计算技术和硬件能力的进步，数值模拟已成为气动辐射预测的重要和有效手段之一。气动辐射模拟一般由4个模块组成：热化学非平衡流动、气体粒子激发态布居、气体光谱特性和辐射传输过程。目前，火星进入气动辐射预测的不确定性主要来自于非平衡流动与光谱特性的物理与计算模型。

高温非平衡流动模拟为辐射光谱计算提供气体密度、多模态温度和组分浓度等参数信息，其计算准确性直接决定光谱计算精度。Hollis和Prabhu以对流热通量预测精度为对象，综述了相关试验研究以及同数值模拟的对比情况，评估了Park化学反应动力学模型，发现对流加热受壁面催化的影响更大，对化学反应和两温度模型不敏感。Johnston等对气动辐射进行了不确定性分析，主要关注化学反应模型和平动-振动松弛模型，发现在进入速度为6.3～7.7 km/s的范围内，驻点辐射加热关于上述模型参数的不确定性为50%～200%，主要由CO离解速率和CO重粒子激发速率造成。基于此分析和电弧激波管(Electric Arc Shock Tube，EAST)的试验结果，Johnston和Brandis提出了新的火星大气化学反应速率模型，CO的离解反应速率被大大提高，结果表明新模型与试验值吻合较好，传统的Park模型明显高估辐射。

光谱特性计算为辐射传输提供发射系数和吸收系数等辐射特性。董士奎等以HITEMP为基础计算了CO窄谱带模型参数。Palmer和Cruden使用NEQAIR(Nonequilibrium Radiative Transport and Spectra Program)计算了中低温条件的CO红外辐射，采用简化CDSD-4000光谱数据库，结果验证了该温度范围内的CO光谱辐射模型。Lemal等结合数值模拟和地面试验预测了CO的非平衡辐射加热，分析了平衡和非平衡条件下的光谱辐射，特别在平衡状态下对比了HITEMP-2000和CDSD-4000等不同数据库，发现使用CDSD的计算结果与试验值符合更好。针对高速非平衡流动的CO反应气体辐射特性尚有大量基于流动场景的模型与试验对比研究需要开展。

精细化光谱辐射强度测量试验是气动辐射研究的重要组成部分，试验获得的基础数据是支撑计算模型验证与确认的关键。Cruden在EAST上开展了速度为6～8 km/s的发射光谱定量测试，和相对低速条件下CO振动红外辐射测量，发现在低密度条件下，绝大多数试验均未达到平衡态。CO真空紫外辐射贡献很大，还有CN辐射，CO振动跃迁引起的中红外辐射则较小。Takayanagi等在HVST(Hyper-Velocity Shock Tube)的模拟火星大气环境中，通过两台光谱仪测量了真空紫外到近红外的发射光谱。还开展了速度2.5～8 km/s范围的CO振动中红外辐射测量，发现激波速度小于6 km/s时，红外辐射随着速度降低而增加。

未来的火星探测进入器具有更大的尺寸和重量，需要采用新的低冗余热防护系统设计，以实现降低发射成本、增加载荷和增强系统稳定性与安全性的目标，那么，更为准确和可靠的气动辐射预测就尤为重要。目前的火星进入气动辐射计算模型尚存在较大的不确定性，用于支撑模型验证与改进的地面试验数据在多样性和广泛性方面也显不足，因此，有必要利用不同地面设备开展更多的精细光谱测量试验，加强试验和数值研究的相互协作，完善和验证计算模型，以此为基础构建准确的火星进入气动辐射预测手段。

1 控制方程与计算方法

1.1 非平衡流动

1.1.1 守恒方程

火星进入流动求解多组分Navier-Stokes方程，考虑热化学非平衡模型。质量守恒方程为

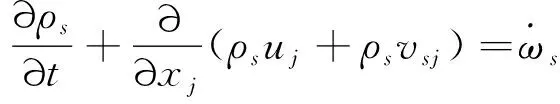
(1)

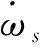
动量守恒方程为

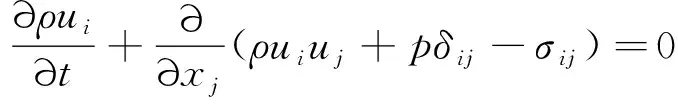
(2)

式中：为密度;为压力；为应力张量分量；为Kronecker符号。

考虑高速流动下内能与平动能处于非平衡状态，能量方程包括内能守恒和总能守恒。内能守恒方程为

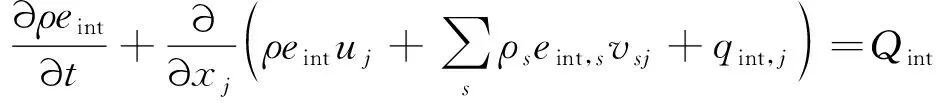
(3)

式中：为质量平均内能；int,为内能梯度引起的方向能量通量；源项代表混合气体中由粒子碰撞过程引起的内能松弛速率。平均内能由各组分内能得到：

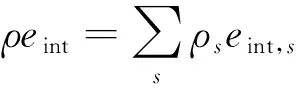
(4)

总能量守恒方程为

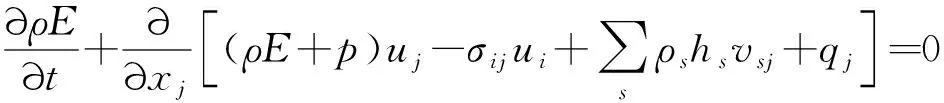
(5)

式中：为能量梯度引起的方向总能量通量；为组分的焓;为总能量，其表达式为

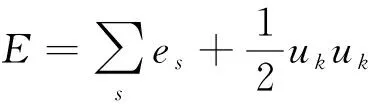
(6)

其中：为组分的总能量，包括平动能、转动能、振动能和电子能，本文采用双温度模型，即平动能与转动能平衡，振动能与电子能平衡：

(7)

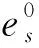
(8)

的表达式为

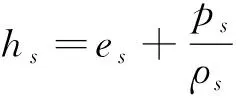
(9)

式中:为组分的压力。

对于质量、动量和能量的输运过程，有

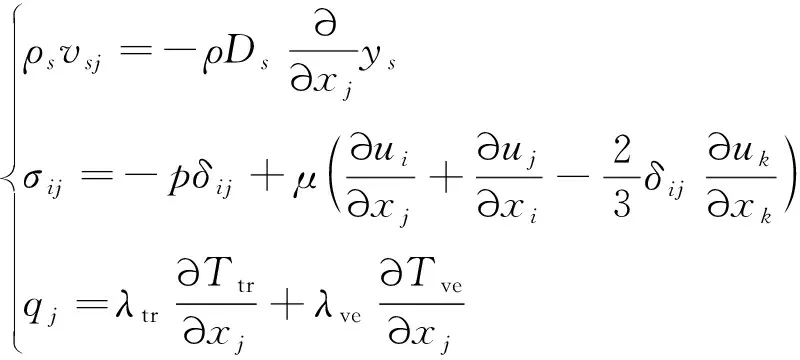
(10)

式中：为组分的摩尔分数；组分的等效扩散系数、黏性系数、平动转动热传导系数和振动电子热传导系数的计算公式与取值参见文献[22]。

1.1.2 源 项

化学反应源项由有限速率化学反应模型计算。将化学反应写为

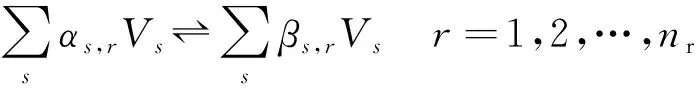
(11)

式中：为化学反应数；,和,分别为反应中组分的化学计量系数。那么单位体积内组分的质量生成率源项为

(12)

式中:为组分的摩尔质量;f,和b,为反应的正向和逆向反应速率：

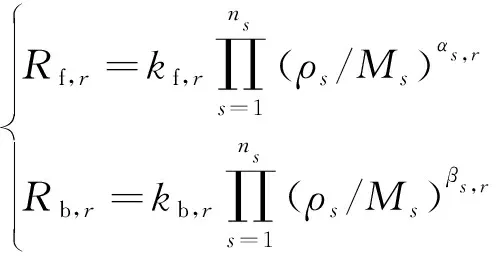
(13)

其中:f,和b,分别为反应的正向和逆向反应速率系数，由Arrhenius反应速率模型得到：

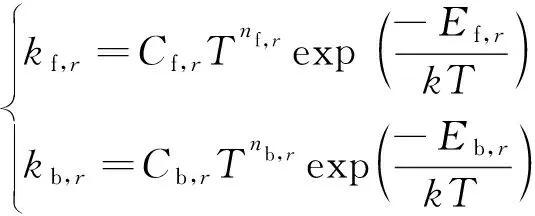
(14)

式中：f,、f,和b,、b,分别为反应的正向和逆向反应速率常数；f,、b,为正向和逆向反应的活化能;为玻尔兹曼常数。

对于火星大气环境，采用Park的8组分(CO、CO、O、O、C、N、N、NO)、9反应模型，具体反应见表1，反应速率常数参考文献[6-7]。

内能松弛源项对于电离气体而言形式非常复杂，对于典型火星进入场景，离子化反应程度不强，可以不考虑离子和电子等造成的内能转换，仅考虑由碰撞过程引起的振动能松弛，该源项一般采用Landau-Teller模型：

表1 火星大气的Park反应模型Table 1 Park’s reaction model of Mars atmosphere

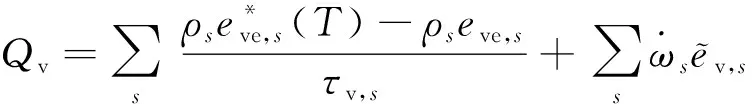
(15)

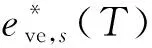
1.1.3 数值方法

采用基于多块结构网格的有限体积法离散计算域，对流项使用van Leer格式，界面值由MUSCL (Monotonic Upwind Scheme for Conservation Laws)方法使用van Albda限制器计算；黏性项采用二阶中心格式；时间推进采用LU-SGS (Lower Upper Symmetric Gauss Siedel scheme)方法；并行使用MPICH实现。

1.2 光谱辐射模型

气体辐射包括原子束缚-束缚跃迁(原子线谱)、原子束缚-自由跃迁(光致电离)、原子自由-自由跃迁(轫致辐射)和分子束缚-束缚跃迁(分子带谱)，并可能包括化学反应发光。火星进入气体辐射的主要来源包括：分子带谱，如CO振动跃迁，CO(4+，真空紫外)，CN(B-X，紫色)、C(Swan，蓝紫色)和CN(A-X，红色)，以及原子辐射，如C和O(紫外-可见-红外)。

对于电子跃迁，采用窄带法计算辐射特性：

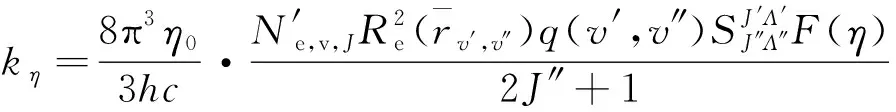
(16)

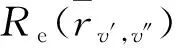
对于振动-转动跃迁，以CDSD数据库为基础进行计算。气体吸收谱线之间会发生部分重叠，在波数处的光谱吸收系数等于相互重叠谱线在波数处的吸收系数,之和：

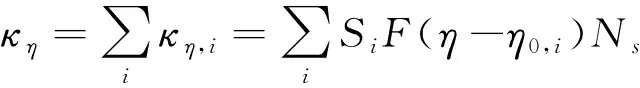
(17)

式中：为标准化为单个分子的谱线积分强度，计算方法和数据库参见文献[11,13]；(-0,)为谱线线型函数,0,为第条谱线的中心波数；为分子数密度。非平衡条件下应用流场模拟获得的平动转动温度和振动电子温度计算配分函数等参数，具体参考文献[7,26]。

1.3 辐射传输方程

存在吸收、发射和散射的非灰气体辐射传输方程为

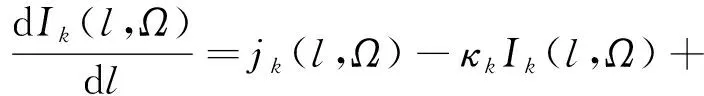
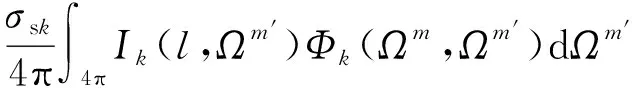
(18)

式中：为辐射强度；为空间位置；为立体角；为谱带发射系数；为吸收系数；s为散射系数；(,′)为散射相函数，其中和′分别为入射角和散射角;下标表示光谱离散的谱带。散射项对计算资源需求非常大，所幸进入气动环境中高温气体的散射非常弱，可忽略，这样极大简化了方程求解。刘林华等通过离散坐标法进行了三维空腔的辐射计算，牛青林等采用视在光线法对滑翔飞行器红外辐射特性进行了模拟。本文基于进入器辐射热流预测需求，选择光线追迹法和有限体积法解算辐射传输方程，以获得特定方向辐射强度和飞行器表面辐射热流分布。

光线追迹法针对一条光线，能够得到流场内沿该传播方向的详细光谱结构和数据，适用于光谱模型的验证。在建立沿一定方向的光线和离散点后，如图1(a)所示，通过流场插值获得节点处的密度、温度和浓度等信息，进而得到发射和吸收系数等，由节点开始计算辐射传输，至节点结束，即得到节点的光谱辐射强度。具体的，根据Beer定律：

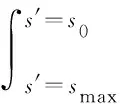
(19)

式中：为频率；为光学厚度：

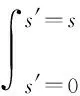
(20)

有限体积法则能够直接获取进入器表面所有位置与空间的辐射通量，并直接利用流场网格与信息，避免插值引起的误差，借助CFD求解框架实现并行计算，适用于进入器热环境评估的辐射强度和辐射热流计算。图1(b)显示了有限体积法在位置空间和角度空间离散辐射传输方程得到的控制体，为内部格心节点，、、、、和分别为表面积分点，角度离散将4π空间分为个立体角，向量为立体角中心矢量。通过简化和数值变换，可得不计散射的辐射传输离散方程：

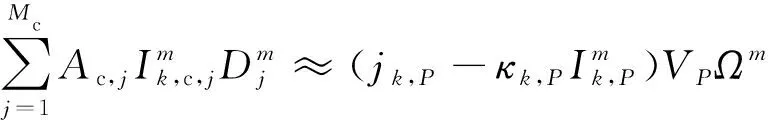
(21)

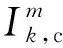
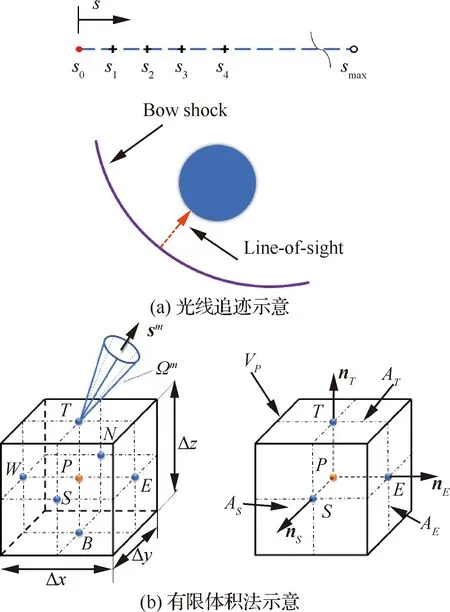
图1 光线追迹法和有限体积法离散Fig.1 Ray tracing and finite volume discretization

2 CO2辐射计算与验证

2.1 光谱辐射强度

采用激波管试验的测量结果验证中高温条件CO光谱辐射计算。试验分别选自NASA Ames研究中心于2014年和JAXA于2018年开展的地面试验。数值模拟使用一个长2 m的激波管为对象，其中充满纯CO气体，利用平衡反应产物作为激波管虚拟驱动气体，进行一维非定常流动模拟，划分1 000个网格点，时间推进采用3阶Runge-Kutta方法。

图2是被驱段压力为133 Pa、激波速度为3.0 km/s 激波管试验状态的模拟结果，分别为压力、温度和各组分质量分数。波后非平衡区比较窄，平动温度和振动温度迅速平衡，平衡温度约3 500 K。此条件下，约10%的CO离解，产物主要为CO和少量的O与O。

图3为激波到达1.55 m位置时，波后10 cm处光谱发射强度的文献测量值和数值预测结果的对比。结果表明，激波速度为3 km/s时，计算得到的光谱辐射结构与文献相符，辐射主要集中于CO的4.7 μm波段，辐射峰值和谱带宽度均与测量结果符合较好，验证了流动及辐射特性计算模型。

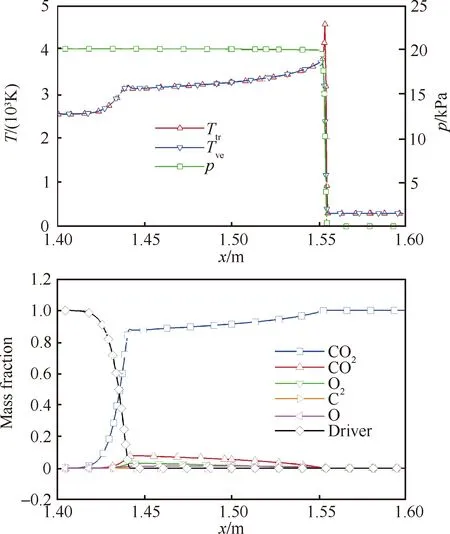
图2 被驱压力为133 Pa、激波速度为3 km/s的激波管流动参数Fig.2 Shock tube parameters at 133 Pa driven pressure and 3 km/s shock velocity

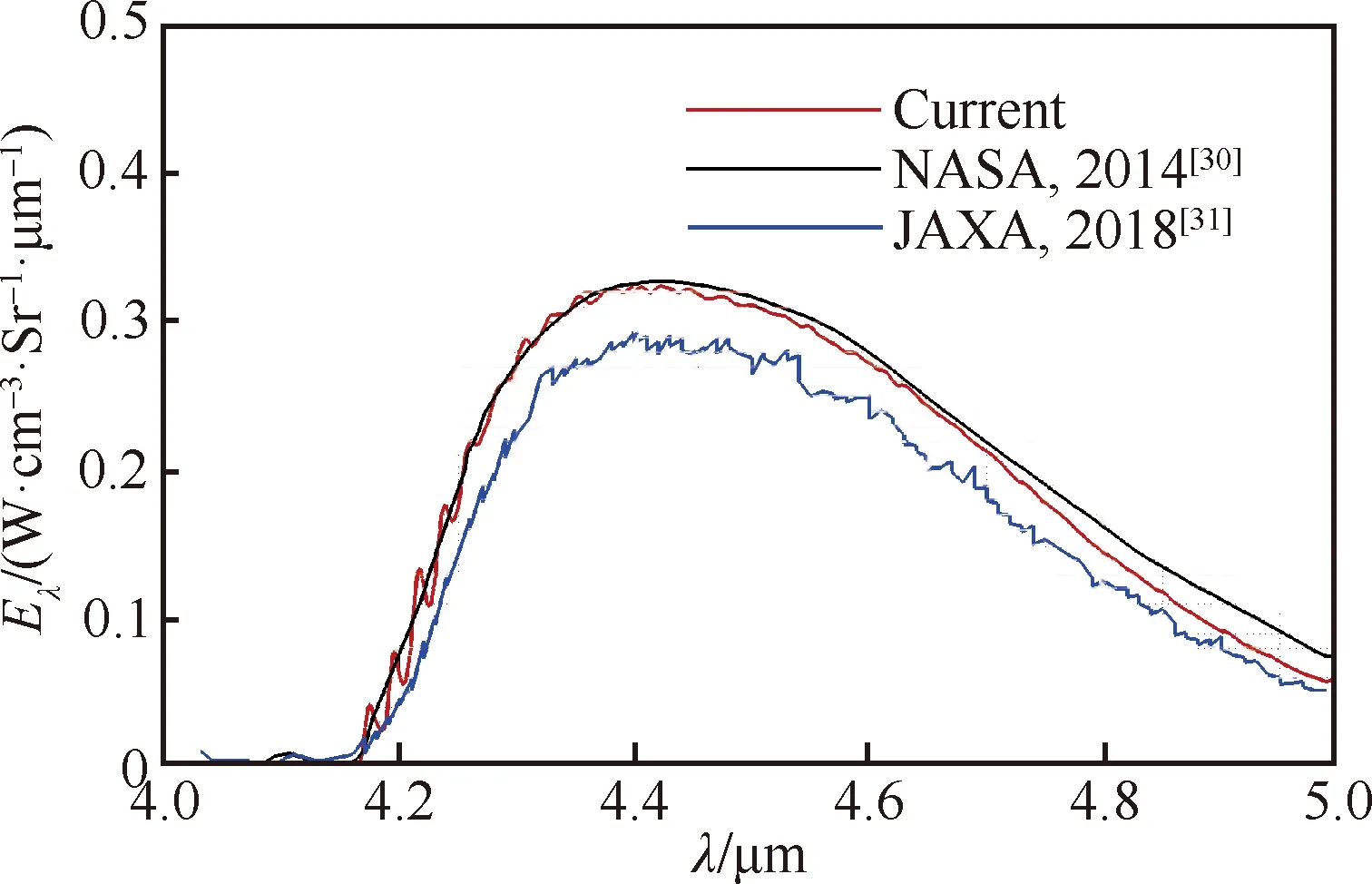
图3 CO2光谱发射强度的计算值与参考对比Fig.3 Comparison of CO2 spectral emission intensity between calculation and reference

2.2 相对辐射强度测量与验证

以CO为试验介质，在典型进入速度范围内，基于燃烧驱动激波管开展了一系列气体发射强度测量试验。相关试验设备和测量方法详见文献[32-33]。被驱动段充入纯CO气体，压力设为300 Pa，通过调节驱动段气体压力以产生所需的激波速度，测得的激波速度范围为3～6.6 km/s。采用滤光片和光电探测器测量气体发射强度，测量位置均位于波后平衡区内。

图4为以4 km/s激波速度的发射强度为参考值得到的归一化发射强度随激波速度的变化，包括计算值、试验测量结果和Cruden等的试验结果。3套数据之间符合较好，进一步验证了火星进入非平衡流动和辐射特性计算模型在不同状态下的准确性。同时，结果也表明，当进入速度小于6 km/s时，发射强度随速度降低而增加，与地球再入的辐射变化规律截然不同，此结论与文献[19]一致。

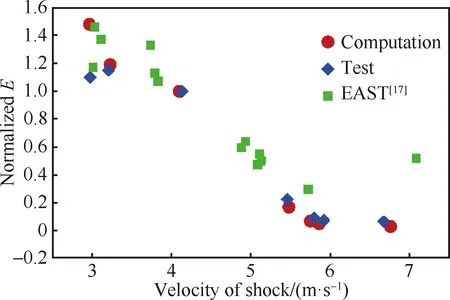
图4 不同激波速度下计算、试验和文献的发射强度E对比Fig.4 Comparison of emission intensity E among computations, tests and reference data under different velocities of shock

3 进入器辐射热流

3.1 模型与计算条件

选择火星探路者号(Mars Pathfinder，MPF)为进入器模型进行数值分析。MPF的前体为直径2.65 m的70°钝球锥，后体为单锥，外形和网格如图5所示。0°侧滑下流场关于=0 m平面对称，因此网格仅考虑半模。周向采用C型拓扑，流向采用C-H网格，表面驻点区为非奇性H型网格。根据初算结果，对网格在边界层和激波附近进行加密，以确保网格正交性、波系平行和分辨率。计算条件见表2，表中为高度，为来流速度，为来流密度，为来流温度，为攻角。

图5 MPF外形和网格Fig.5 Configuration and mesh demonstration of MPF

表2 MPF计算条件Table 2 Computational conditions for MPF

3.2 网格收敛性

针对MPF前体外形，生成了3套网格，具有不同的壁面法向最小网格长度和法向网格数目，法向网格最小距离()分别为10m、10m和10m，法向网格数目分别为121、121和201。图6显示了数值计算得到的表面对流热流()沿径向的变化，图7是辐射强度沿驻点线的变化。可见，3套网格的计算结果相差不大，最小距离10m和10m网格的计算结果非常接近，综合考虑计算精度和速度，以下分析均使用10m网格进行计算。

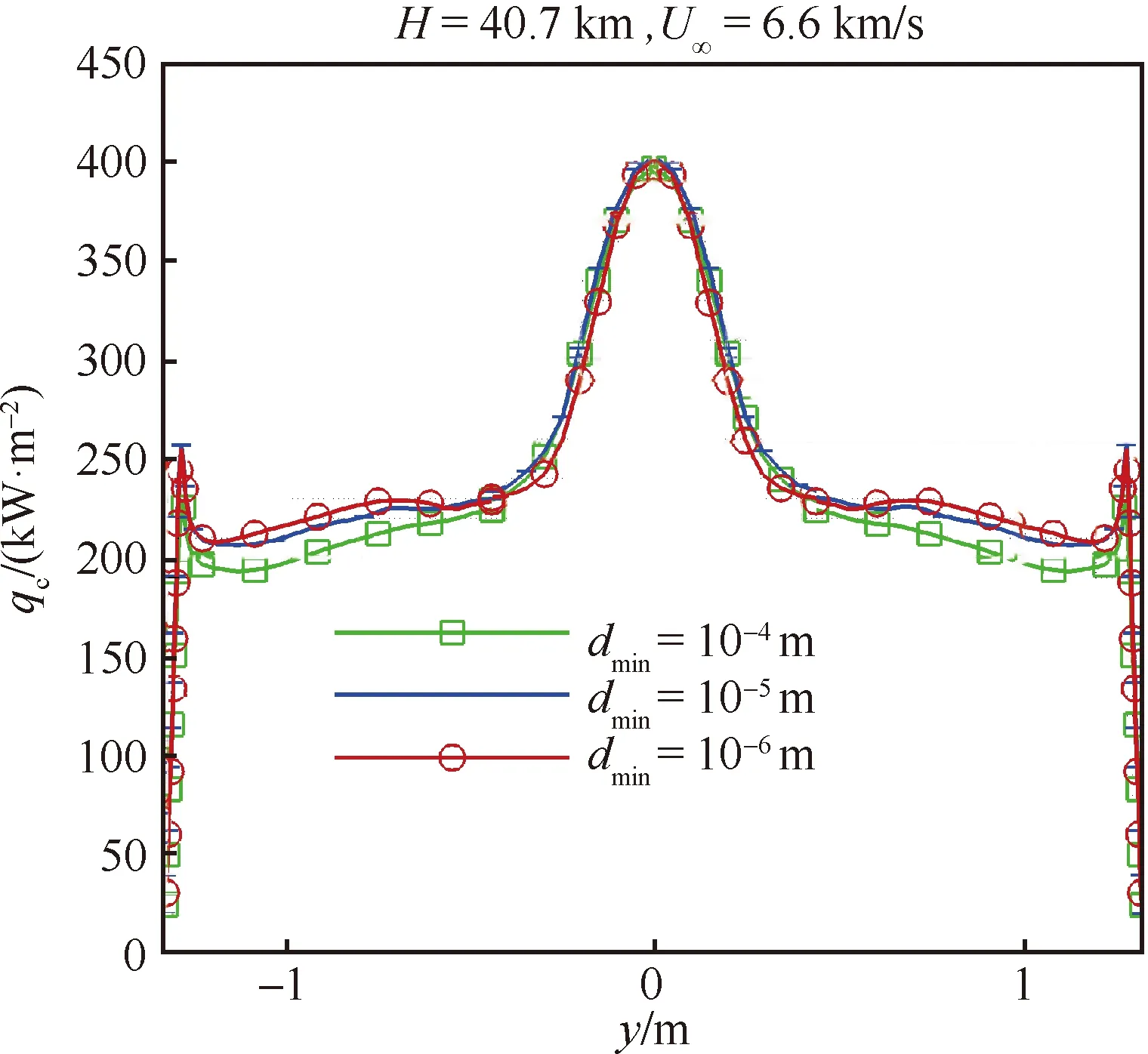
图6 不同网格的表面对流热流Fig.6 Surface convective heating flow for different grids

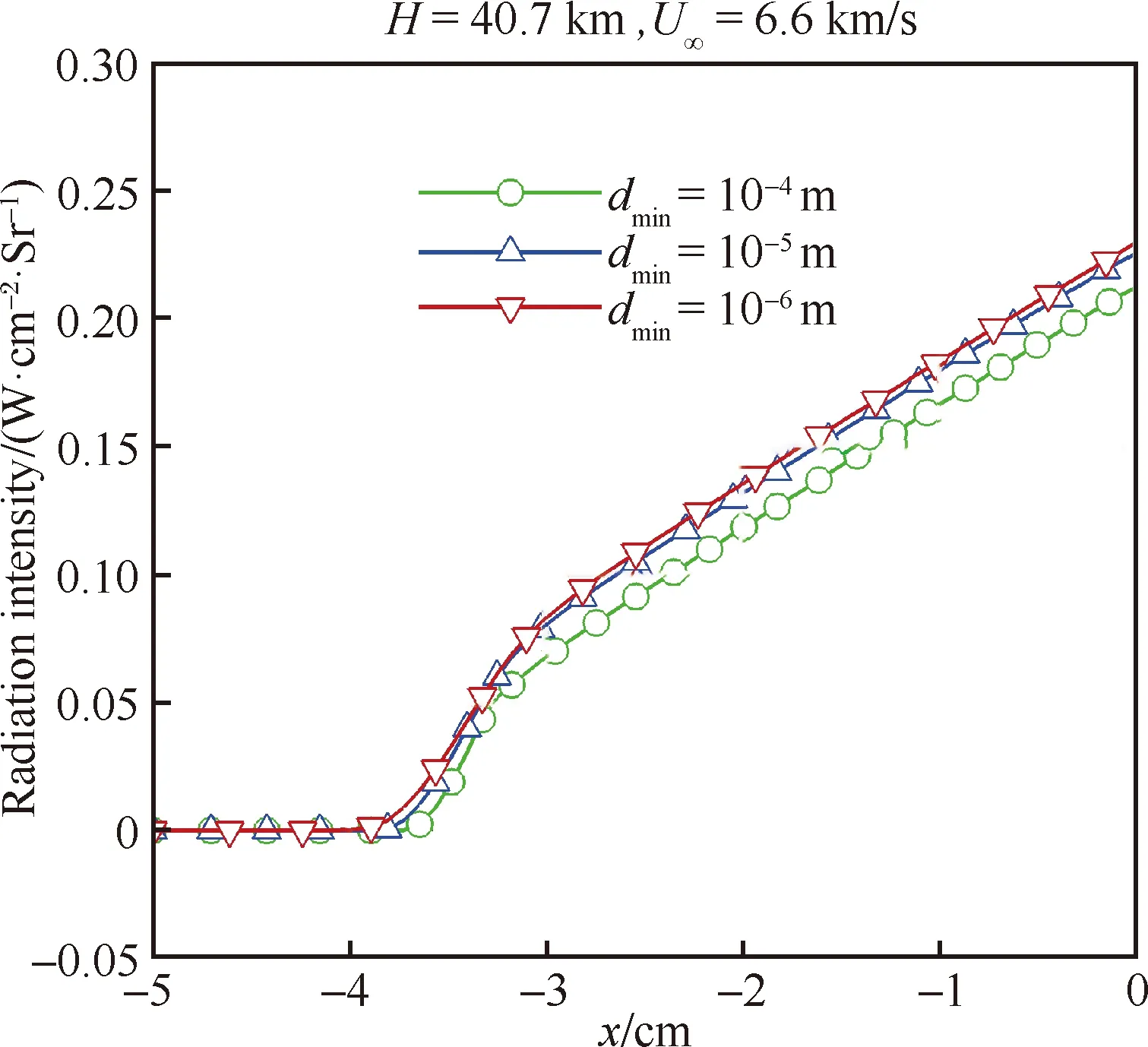
图7 不同网格的驻点线辐射强度Fig.7 Radiation intensity along stagnation line for different grids

3.3 流动与辐射加热

图8和图9分别是两种进入速度的对称面流动参量分布，包括温度和CO质量分数。不同的激波强度导致激波层内气体温度和组分浓度差异明显。高速条件下，激波层气体温度超过7 000 K，在这种高温条件下化学反应剧烈，CO完全离解，进入器周围主要为CO、O和O。尾流中气体由于快速膨胀，温度迅速降低至约2 000 K，此处气体主要为由上游流至，由于流动速度很快，复合反应没有足够时间展开，因此，CO仍维持完全离解状态。在尾流中心处，旋涡结构及其上方的剪切结构导致气体温度升高至4 000 K左右，此处气体较少来自上游，而当地气体由于缺少激波压缩，密度较低，化学反应程度较弱，因此CO离解程度相对稍低。低速条件下，激波层厚度明显增加，尾流呈现更为明显的剪切和反射激波，激波层和尾流核心区内的气体温度都在1 500 K左右，虽然低空的气流密度更高，但温度较低导致CO基本没有离解，进入器周围主要为CO。

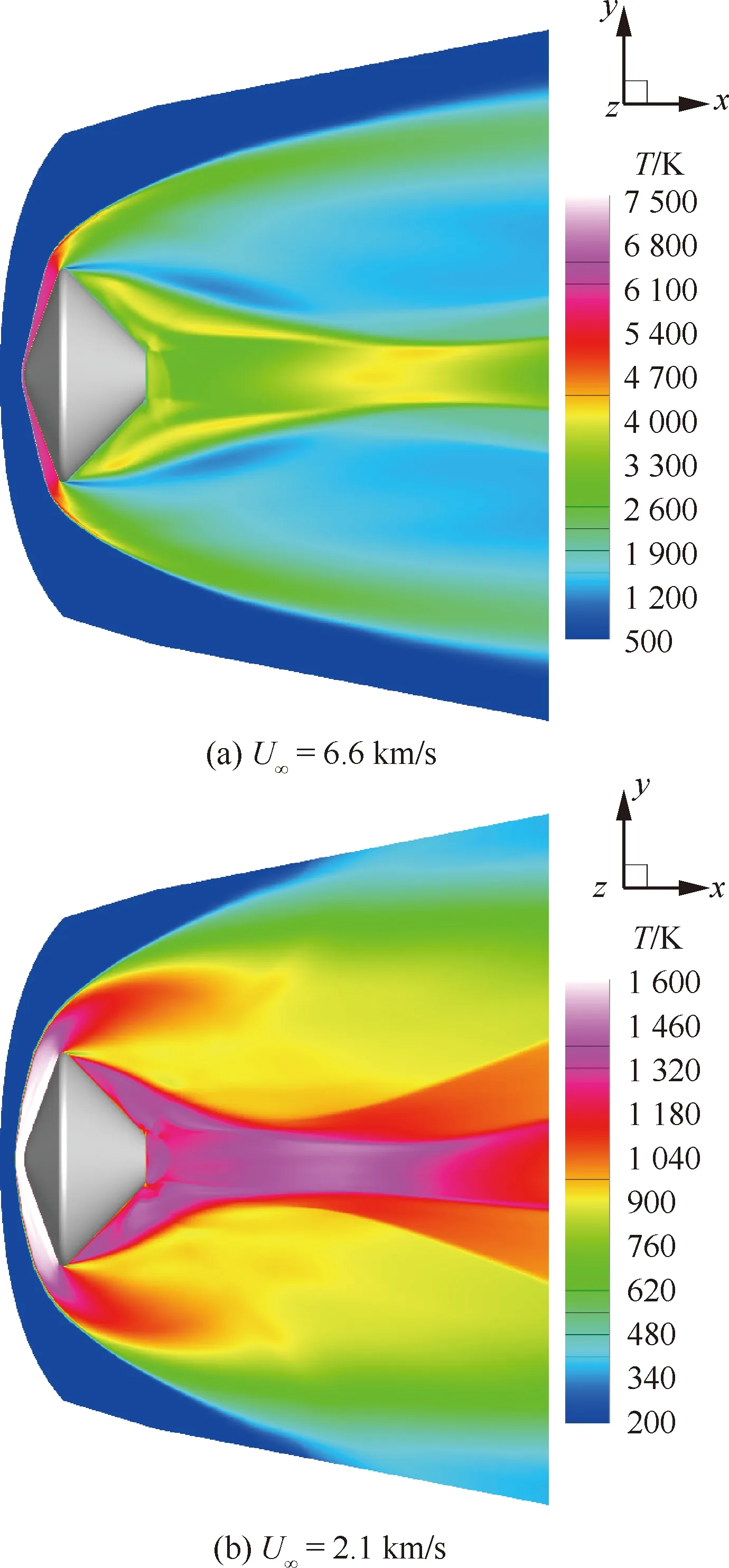
图8 MPF对称面温度分布Fig.8 Temperature distribution in symmetry plane of MPF

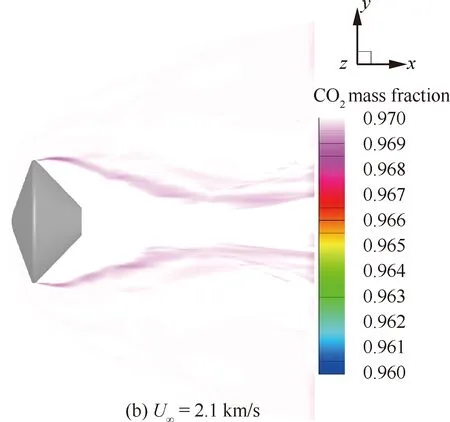
图9 MPF对称面CO2质量分数分布Fig.9 CO2 mass fraction distribution in symmetry plane of MPF

考虑沿驻点线传播的光线，建立光线追迹网格，获取相关流场参数，如图10(a)所示，分别为2个状态对应的温度和组分质量分数沿驻点线的变化。对该光线进行辐射特性和辐射传输计算，得到如图10(b)所示的辐射强度变化，可见随着光线进入激波层并向壁面传播，高温气体不断发射辐射能量，辐射强度逐渐增大，最终传输至边界层，考虑到边界层内气体温度较低，对辐射传输的影响较小。

图10 流动参量和辐射强度沿驻点线变化Fig.10 Variations of flow parameters and radiation intensity along stagnation line

图11对比了2个速度状态的驻点总光谱辐射强度，结果显示速度为2.1 km/s时，虽然气体温度远低于高速条件，但红外段的辐射强度远大于高速条件。速度为6.6 km/s时，短波光谱有明显升高，对辐射产生更大的影响。

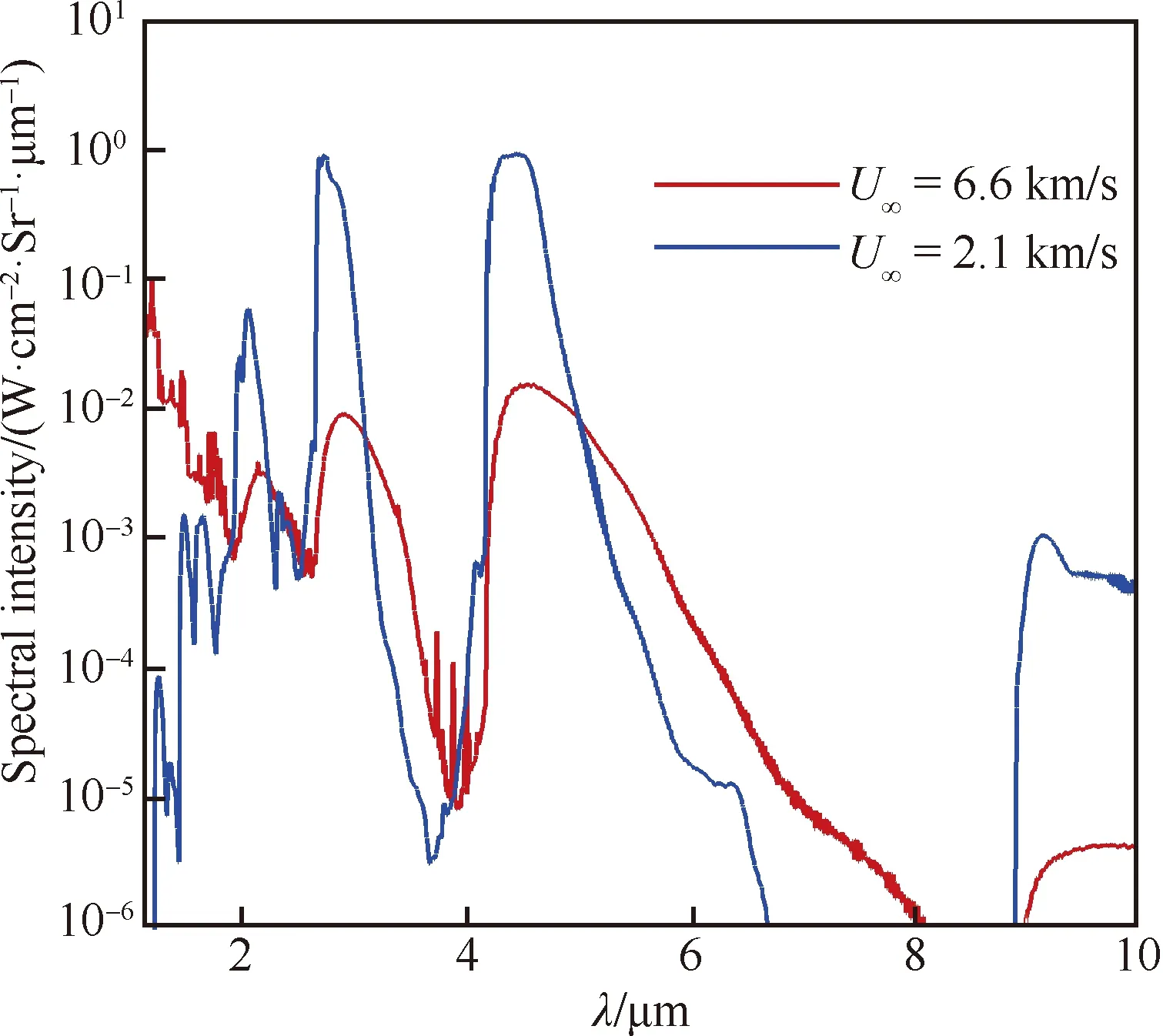
图11 不同速度的驻点光谱辐射强度Fig.11 Spectral radiation intensity at stagnation point for different velocities

图12为速度6.6 km/s状态的驻点光谱辐射强度随波长的变化，由于对CO(4+)的真空紫外辐射尚未完成验证，因此谱带并未包括真空紫外段。辐射能量主要集中在波长2.5～3.5 μm和4～6 μm的红外谱段，由CO和CO叠加形成，O、N等原子和O、N等分子的电子跃迁谱线集中于波长2 μm以下的短波区域。

图12 速度6.6 km/s状态驻点光谱辐射强度Fig.12 Spectral radiation intensity at stagnation point under 6.6 km/s

图13为速度2.1 km/s时CO和CO产生的驻点光谱辐射强度。可见低速时，由于流场内组分基本是中等温度的CO，故辐射基本完全由CO产生，其强度远高于其他组分。对比图12，高速时高温及离解产生的CO成为重要的辐射来源，因此，对于火星进入，高速和低速条件产生的非平衡流动及其辐射机制是完全不同的。

图13 速度2.1 km/s状态驻点光谱辐射强度Fig.13 Spectral radiation intensity at stagnation point under 2.1 km/s

基于流场计算结果，在所有网格点进行发射系数和吸收系数的计算，根据Planck平均公式得到0.2～10 μm光谱范围内的平均吸收系数，对称面分布如图14所示。吸收系数分布和流场结构高度相似，发射较强的区域一般为高密度且高温度区域，例如，高速条件下，吸收系数较大的区域为激波层和尾流剪切层，核心区密度较低，因此吸收系数也较低。低速条件下激波层内的气体吸收系数明显高于其他区域。

图15分别为进入速度6.6 km/s和2.1 km/s的前体和后体表面辐射热流()分布。高速时，前体激波层较薄，虽然气体温度很高，但CO完全离解，辐射热流较低，峰值热流出现在后体邻近肩部处，主要来自尾流中大范围的中高温气体。同时，由于球锥外形的驻点区激波层较锥体更薄，导致驻点辐射热流低于锥体。低速时，CO未离解，气体辐射主要来自CO的贡献。激波层和尾流的温度接近，但尾流密度明显小于激波层，导致前体辐射热流高于后体。同样的，虽然驻点区与锥体的激波脱体距离差异不如高速时明显，但驻点区辐射热流仍小于锥体。另外，驻点区辐射热流在低速条件下高于高速条件，这与激波管试验的结论一致。

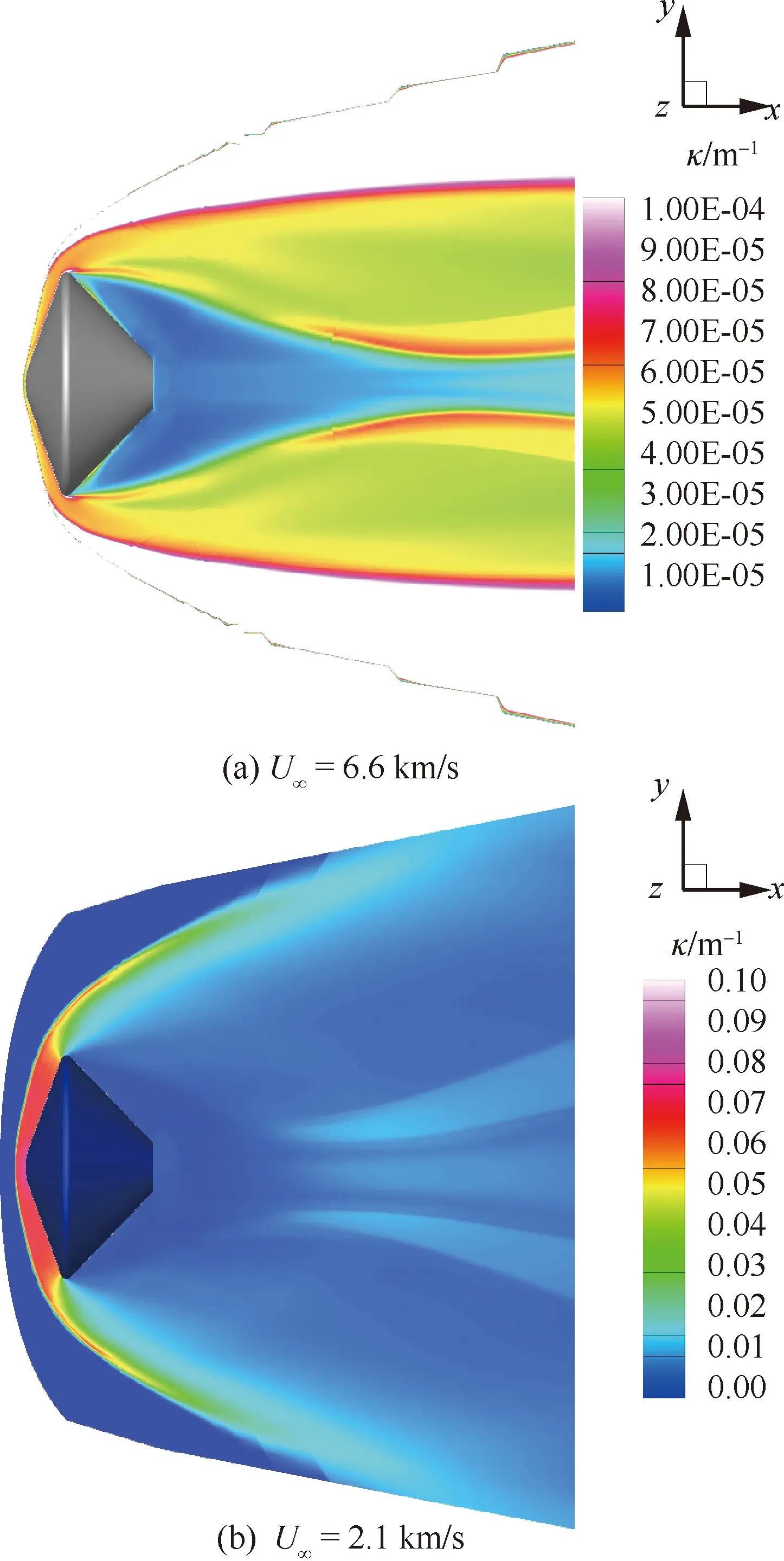
图14 对称面平均吸收系数分布Fig.14 Average absorption coefficient distribution in symmetric plane

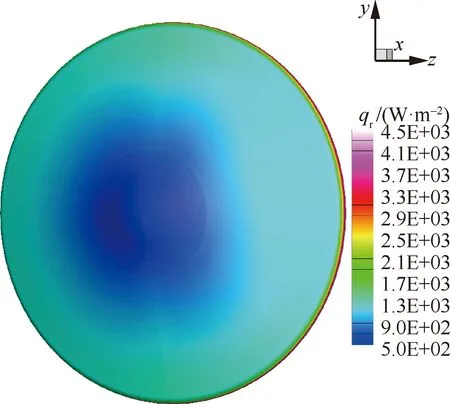
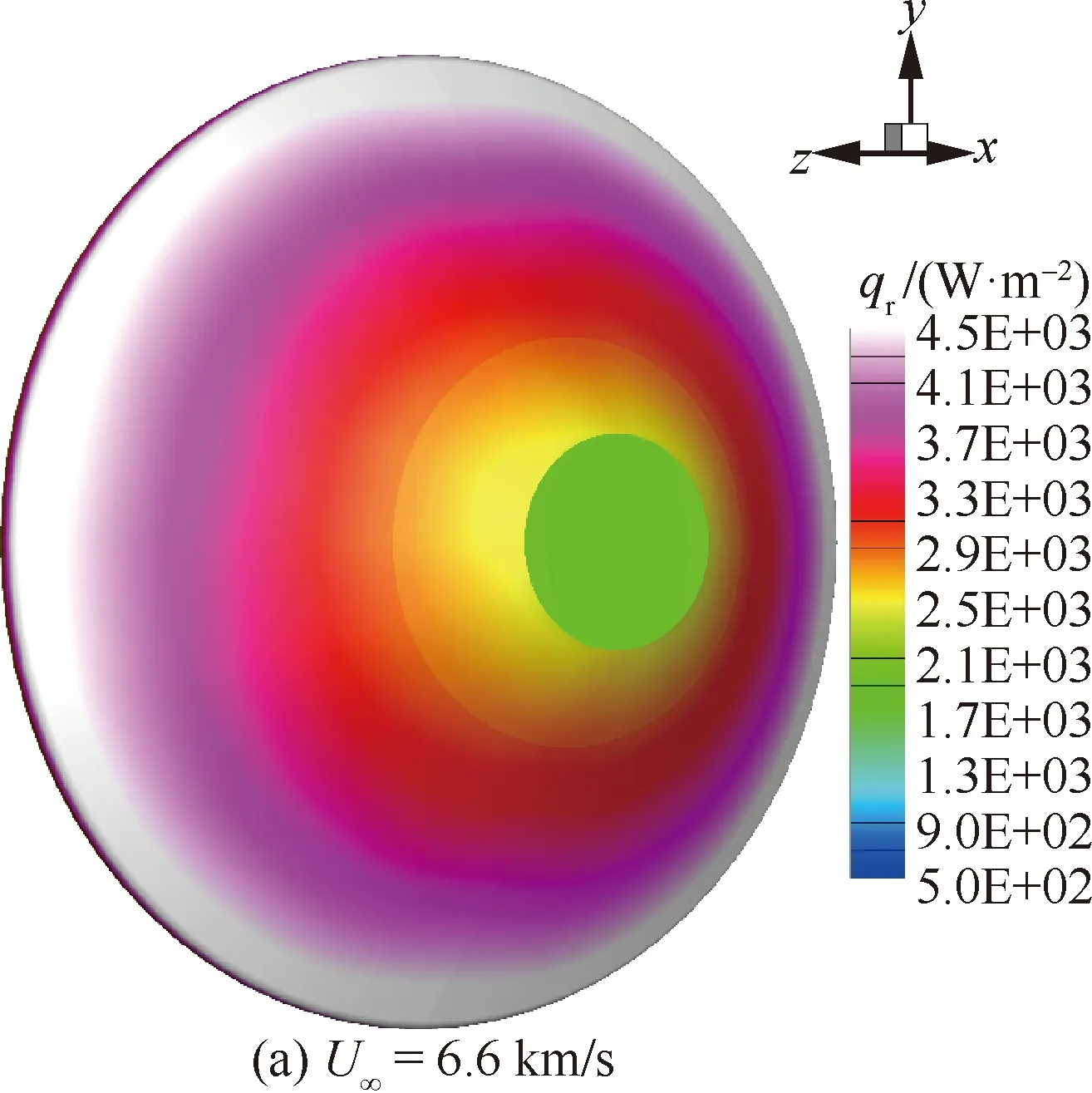
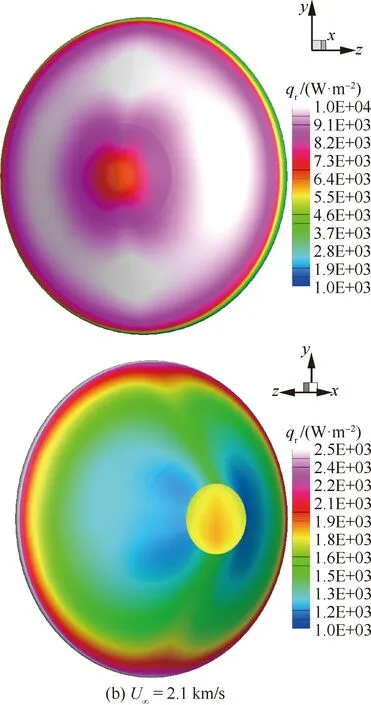
图15 前体和后体表面辐射热流Fig.15 Radiative heating rate on fore and aft surface

4 结 论

对典型火星进入条件的气体光谱辐射结构和辐射加热开展了数值和试验研究，得到以下结论：

1) 建立了火星大气气体光谱特性模型，计算结果与文献数据在光谱结构和辐射强度上均符合较好，验证了数值模型，CDSD光谱数据库适用于火星进入光谱计算。

2) 通过激波管地面试验，获得了不同激波速度的辐射强度测量结果，与计算值和文献数据符合良好，结果表明火星大气进入速度低于6 km/s时，气体辐射随进入速度减小而增大，和地球再入规律不同。

3) 针对MPF典型进入状态，开展了高速和低速进入的非平衡流动、辐射特性和辐射传输模拟。发现驻点区辐射热流小于锥体，低速进入的辐射主要由CO形成，高速进入的辐射由CO和CO共同主导，低速进入的驻点辐射热流高于高速条件的，高速时辐射峰值热流出现在后体的肩部附近，低速时则出现在前体的锥体，以上规律可辅助火星进入器的热防护系统设计。