水风光多能互补联合运行增益分配研究

陈述，赵金凡，陈云*，习俊博，周露，崔洁

(1.三峡大学水利与环境学院，宜昌 443002；2.三峡大学经济与管理学院，宜昌 443002)

随着电力系统的日益扩大、化石能源的储量逐渐减少，以风电、光伏为主的可再生能源受到广泛关注并迅速发展。然而，单一新能源发电难以实现高效、稳定、可靠的电力输出目标[1-2]。为维持电力系统安全稳定和供需均衡，融合能源间的互补特性，保证各利益主体间坚实合作和稳定联盟是不可忽视的重要问题，而合理分配各主体获得的收益是实现有效联盟的关键[3-4]。因此，开展多能互补系统收益分配研究，具有重大现实意义。

多能互补运行是未来电力系统发展的必然趋势，中外众多学者已开展了大量研究。文献[5]首次提出水电和风电联合运行的模式，论证了联合运行的可行性。文献[6]利用电源之间的互补特性，提出将新能源和常规电源打捆调度，以达到电力系统安全稳定运行。文献[7]针对风电和光电出力的不确定性，直接并网会对电网的安全稳定运行产生较大冲击。水力发电具有快速响应、调节性良好和输出功率稳定等特点，已成为互补能源的首选。文献[8]根据水光火出力的互补特性和配比，建立了衡量多能发电系统互补出力特性的效果指标。文献[9]为提高风光水发电系统的经济效益，基于决策变量和影响因子属性集，构建了误差反向传播算法(back propagation，BP)人工神经网络模型提取调度规则。文献[10]为解决能源系统调度中可再生能源机组出力和负荷不确定性问题，建立多能源微网调度优化模型。文献[11]基于多种能源协调运营、发电成本、上网电价及辅助服务收益，构建包含风电、光伏和抽水蓄能电站收益的多目标函数，以降低市场运营风险，获得较好的收益。

现有研究主要从多能互补运行、优化配置、经济调度等方面展开研究，对于水风光多能互补联合运行利益分配方面研究较少。因此，选择公平、合理的利益分配方法是保证各利益主体间坚实合作是不可忽视的问题，是实现各发电企业利益最大化有利途径。鉴于此，现基于合作博弈理论，对水风光多能互补联合运行进行博弈分析，构建水风光多能互补增益函数和电站收益函数，结合多能互补发电系统的运行特点，利用互补系数对联合发电互补性进行评价，分析不同分配策略下联盟的增益分配值和分配策略的吸引力，并选择最优分配策略对联盟增益进行分配以实现参与主体经济效益最大化。从而提升风电、光电企业效益，保证各主体利益分配均衡。

1 水风光多能互补运行博弈分析

在水风光多能互补联合运行中，水电站、风电场和光伏电站作为三家不同利益主体运营管理，参与主体都希望通过博弈行为使自身收益最大[12]。在博弈论中，非合作博弈适用于竞争状态下不考虑其他参与主体时各自策略的制定。而合作博弈偏向于合作过程中，考虑所有人利益情况下整体或联盟的收益分配，在电力行业中的输配电竞价、系统费用分摊、增益分配等领域应用广泛。

1.1 博弈要素分析

在多能互补博弈过程中，合作博弈的基本要素是构成合作博弈的先决条件，即博弈主体、结构、原则等。本文研究中将水电、风电和光电发电企业作为参与主体，分别用符号W、F、G表示，则参与主体集合为{W,F,G}，在三方博弈中共有五种联盟结构，如表1所示。

表1 水风光多能互补联合运行博弈联盟结构

1.2 博弈结构分析

基于合作博弈理论体系，根据水电、风电、光电等新能源发电特性和电力体制改革，水风光多能互补联合运行博弈过程如图1所示。

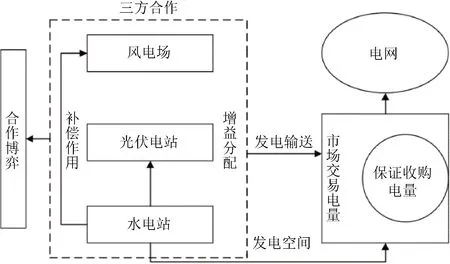
图1 水风光多能互补博弈过程图

利用水电的调节作用克服风电与光电出力存在的间歇性和不稳定的缺点，促进光电、风电的消纳，以保证水风光多能互补的供电质量[13]。并通过联盟形式向市场供电，以保证风电和光电安全并网。当风电和光电获得发电空间后提高了经济收益，适当补偿水电。

1.3 多能互补增益

多能互补增益主要是指水风光多能互补联合运行时的发电效益较电站独立运行时发电效益的增量收益[14-16]。同时，电站在进行多能互补运行过程中也伴随着独立运行，具体多能互补增益和电站收益如下。

(1)多能互补电站增益。多能互补运行的增益为

(1)

(2)电站收益。水电站、风电场和光伏电站在参与多能互补运行系统后各电站的经济收益包括两部分，即参与联盟的收益和部分时段独立运行时收益。

B(i)=B0(i)+δi

(2)

式(2)中：B(i)为电站i最终所得发电收益值；B0(i)为电站i独立运行时的收益；δi为总增益的分配值。

1.4 多能互补增益分配原则

多能互补主体联盟在进行增益分配时，必须遵循公平、合理、高效的原则和要求。

(1)公平性：在联盟中，参与主体i分配到的收益与主体联盟中的贡献成正比，即参与主体i对联盟φ的边际贡献为π(i)=v(φ)-v(φ/i)。

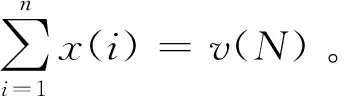
(3)高效性：联盟中各主体分配到的增益总和应等于联盟合作的增量效益。

2 互补性评价指标

多能互补性指标是联合发电系统运行特性的评估基础，是对电站互补程度的判断，互补性越高，则联合运行发电系统的并网运行对电网和自身越有利。本文采用互补系数法对水风光多能互补运行的互补程度进行量化[17]。

互补系数法[18]是指在某时间段内，用来量化评估多能互补联合运行系统发电功率的互补程度。

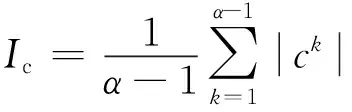
(3)

(4)

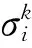
3 多能互补增益分配策略

在多能互补增益分配中，不合理的分配策略会导致一些参与主体有脱离联盟的动机，同时，大联盟会存在被子联盟代替的可能性。因此，采用三种典型分配策略计算水风光多能互补联合运行合作博弈的增益分配情况，通过动态规划(dynamic programming，DP)指标定量描述参与主体对分配策略的接受程度，并选择合理、有效的分配方法，保证分配的可行性。

3.1 等分策略

等分策略即联盟中参与主体平均分配到联盟增量的方法，即

(5)

式(5)中：在水风光多能互补联盟中，x(W)为水电站获得的增量分配；x(F)为风电场获得的增量分配；x(G)为光伏电站获得的增量分配；v({W,F,G})为联盟总增益。

3.2 按容分配策略

按容分配策略是指参与主体i分配的收益v(i)与大联盟后的容量成正比。如水电站的收益分配为

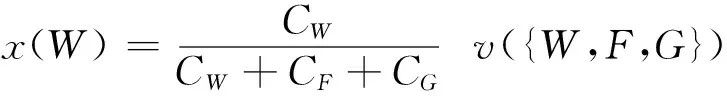
(6)

式(6)中：CW、CF、CG分别为参与联盟水电站、风电场和光伏电站的装机容量;同理可得风电场和光伏电站的分配值x(F)、x(G)。

3.3 Shapley值分配策略

Shapley值分配策略根据参与主体对联盟的边际贡献分配收益，过程清晰，易于理解，因此优先考虑利用 Shapley值分配策略对增益在联盟中进行分配。

根据参与主体i对联盟的平均边际贡献决定所获得的收益，贡献越大获得收益越高[20-21]，即

[v(φ)-v(φi)]

(7)

式(7)中：xi为参与主体i获得的增益分配值;|φ|为联盟中的参与主体数目。

水电站的增益分配为

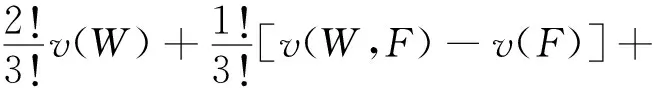
(8)

式(8)中：x(W)为水电站的收益分配值；v(W)、v(F)、v(G)分别为水、风、光各电站独立运行收益；v(W,F)为水、风联盟的收益；v(W,G)为水、光联盟的收益；v(F,G)为风和光联盟的收益；v(W,F,G)为大联盟的收益。同理可得，风电场、光伏电站的收益分配值v(F)和v(G)，即得分配向量x={v(W),v(F),v(G)}。

3.4 分配策略倾向程度分析

分配策略倾向分析主要通过DP指标来定量描述参与主体i对不同分配策略的倾向程度。一般而言，分配策略下的DP指标数值越小，参与主体i接受该方法的可能性越高[22]，即

(9)

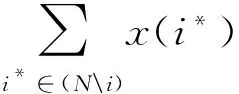
4 算例分析

4.1 研究区概况

青海省清洁能源丰富，是多能互补试验的最佳选择之地，青海海南藏族自治州有水电站、风电场和光伏电站三家不同利益主体运营管理，分别为水电站W、风电场F和光伏电站G，三家企业决定联合实行互补运行。具体技术信息如表2所示。

表2 水风光多能互补电站基本技术信息

4.2 联盟经济效益情况

根据该地区电站的基本技术信息情况，选取该地区典型日进行计算，得出不同联盟方式下的互补系数，如表3所示。

表3 不同联盟方式下的发电系统互补系数

由表3可知，在联盟结构中，风光联盟的互补系数最高，则表明风光互补的程度较低，互补效果不佳，联盟不稳定。而水风光大联盟的互补系数是所有联盟中数值最小值，表明大联盟互补性能最好，互补效果最佳，则在互补博弈联盟过程中，选择水风光大联盟优于其他联盟。

在水风光多能互补联合运行中，合作博弈前后收益变化情况是分析参与主体是否参与联盟的决定因素。本文研究中主要计算了参与主体在博弈前后的收益、发电量以及单位电量收益变化情况，具体如表4所示。

从表4中可知，联盟收益情况均满足博弈的个体理性和整体理性。针对水、风、光三种能源实行多能互补联合运行后产生的收益问题，可以看出合作博弈均存在净增收益。三方联盟优于两方联盟优于各电站各自为政，且在大联盟中，单位电量收益提高最为明显，由0.038 元/(kW·h)提高到了0.105 元/(kW·h)。

表4 不同联盟结构下电站的互补运行发电收益

计算水风光多能互补系统博弈的特征函数与边际贡献，如表5所示，其中，空集0为参与主体集合N的子集，记v(i)=0，参与主体i各自为政的联盟价值也为零，表示没有任何参与主体i可以靠自身而获得高收益。

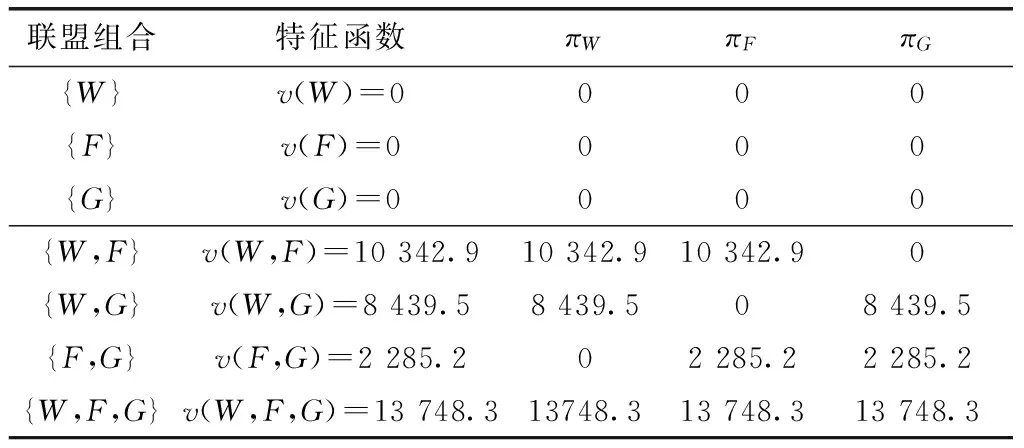
表5 不同联盟方式下特征函数与边际贡献

4.3 增益分析

在水风光多能互补联合运行中，通过计算等分策略、按容分配策略和Shapley值分配策略三种分配策略下水电站、风电场和光伏电站的增益分配值和DP指标，如图3所示。

如图2所示，在等分策略中，参与主体是平分联盟所获得的利益，忽略了各主体在联盟中的贡献，不符合实际情况。根据水电站、风电场和光伏电站的装机容量和发电量等信息和不同联盟下边际贡献可知，水电站在多能互补发电系统中为最大，具有主导地位，且贡献最大，一般优先选择水电站增益分配额最大的方案。在Shapley值分配策略中，各电站在发电增益中的边际贡献值进行分配，水电站在联盟增益中的贡献最大，分得增益最多，风电场次之，光伏电站则分的最少，故选择Shapley值分配策略更符合实际情况。

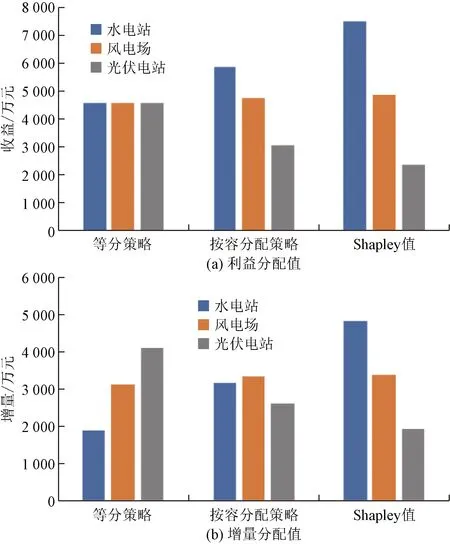
图2 不同分配策略下互补电站收益分配图

如图3(a)中，在等分策略中，水电站的DP值高于1，表明对于水电站而言，水电站拒绝接受等分法分配方案。风电场和光伏电站的增益分配额均高于按容分配法且低于等分策略，水电站发电量占比多能互补发电系统中为最大，具有主导地位，贡献最大，故优先选择水电站增益分配额最大的方案。

根据分配策略倾向程度指标DP值可知，当DP值越小，参与主体对这种分配策略的倾向程度越高，更愿意参与联盟。通过图3(b)中线性趋势可知，在三种分配策略下，光伏电站都倾向于参与联盟且接受均程度高于风电场、水电站，即电站接受多能互补联盟的倾向程度为：光伏电站>风电场>水电站。

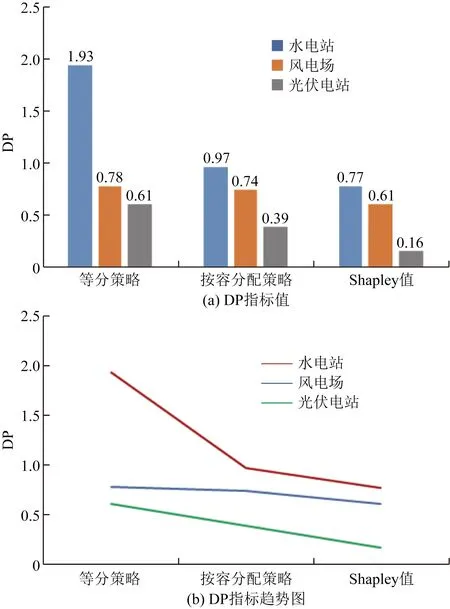
图3 不同分配策略下互补电站DP指标

5 结论

分析了水风光多能互补联合运行进行博弈分析，构建水风光多能互补增益函数，并利用互补系数对联合发电互补性进行评价。同时，分析了不同分配策略下联盟的增益分配值和分配策略的吸引力，选择了最优分配策略对联盟增益进行分配以实现参与主体经济效益最大化。通过实例研究了水风光多能互补运行增益分配问题，得出以下结论。

(1)通过互补系数可知，水风光多能互补大联盟互补性能最好，互补效果最佳，互补性优于其他联盟结构。同时合作博弈使联盟总收益增加，三方联盟优于两方联盟优于各电站各自为政，且单位电量收益明显提高。

(2)在三种增益分配策略中，Shapley值法按各电站在发电增益中的边际贡献值进行分配，水电站在联盟增益中的贡献最大，分得增益最多，风电场次之，光伏电站则分的最少。

(3)根据互补电站DP指标值和趋势图中可知，在不同分配策略下，光伏电站都倾向于参与联盟且接受程度均高于风电场、水电站，即电站接受多能互补联盟的倾向程度为：光伏电站>风电场>水电站。

在研究水风光多能互补联合运行增益分配的过程中，没有考虑输电上网远距离输送等外部因素的影响，仅从电站收益角度对多能互补运行模式的收益进行探讨。因此，考虑远距离输电情景下水风光多能互补运行增益研究将为下一步研究方向。