例谈幼儿园数学游戏的设计与实施

陈斐

陶行知先生曾提出过一个著名的论点：“儿童社会要充满简单之美。”幼儿的思维比较简单，对事物的理解都是从具体到抽象、从简单到复杂。幼儿园应根据幼儿的认知特点，遵循他们学习数学的路径和发展规律，设计易于他们理解和接受的数学游戏，使他们在轻松愉快的游戏中发现数学问题并尝试解决，从中获得数感、分类、测量、几何等的能力和经验。

一、关键经验是数学游戏设计的基础

关键经验是幼儿数学学习与发展必须获得的经验，这些经验在幼儿的经验系统或经验结构中起到节点和支撑的作用，有利于其数学经验的建构、迁移以及对数学知识的深层理解。关键经验具有适应性与连贯性的特点：适应性是指幼儿学习的关键经验要与他们的思维发展特点相一致，和他们的最近发展区相适应;连贯性是指关键经验之间的纵向联系（新经验的学习建立在旧经验基础之上）和从属关系（在层次结构中下层经验是上层经验形成的组成部分）。

数学游戏要围绕各年龄段幼儿所要发展的关键经验进行设计，使不同年龄段的幼儿在与物和人的互动中不断获得和积累关键经验。比如：大班数学游戏“老狼老狼几点钟”所指向的关键经验是让幼儿应用已有的数经验（单双数、数的分解与组合、目测数群等）解决游戏中出现的问题;小班数学游戏“马兰花”所指向的关键经验是让幼儿手口一致地点数4个以内的实物，并能说出总数和理解数与量的对应关系。

二、规则与玩法是数学游戏实施的保障

规则是游戏活动的灵魂，是游戏活动顺利开展的重要保障。教师要充分考虑幼儿的年龄特点和心理特点，制定游戏规则，并使数学游戏的玩法和难度符合幼儿的最近发展区，能发展幼儿的数学关键经验。在每次数学游戏之前，教师要和幼儿明确游戏规则和玩法，让他们知道游戏可以怎么玩，并用規则约束自己和同伴。比如：在开展数学游戏“老狼老狼几点钟”之前，教师和幼儿约定的游戏规则是：时间到12点钟，小羊才能逃回羊圈原地坐下且不能再走动;两个羊圈中的小羊数量一样多则小羊胜，小羊数量不一样多则老狼胜。同时，教师向幼儿讲解了游戏的玩法：幼儿扮小羊，老师扮老狼;游戏开始，小羊围着羊圈边走边问老狼时间，老狼在山洞里回答;当小羊听到12点钟时，马上逃回羊圈原地坐下，老狼倒计时“3、2、1”后冲出山洞抓小羊……

幼儿按照一定的规则进行数学游戏，应用已有数学知识和经验解决数学游戏中的问题，又在解决问题的过程中提升和发展了自己的数学知识和经验。比如在用皮球玩数学游戏“马兰花”中，小班幼儿运用已有的数数经验，能手口一致地点数5个以内的皮球，还能按照教师或同伴说的数字准确取出相应数量的皮球，从而发展了感知和理解数、量及数量关系的能力和经验。

三、策略和方法是数学游戏成功的要素

（一）情境导入法

数学具有抽象概括的特征，而幼儿又以具体形象思维为主。他们需要从各种各样的情境和感性环境中获得并应用数学的经验。《幼儿园教育指导纲要（试行）》提出要使幼儿“能从生活和游戏中感受事物的数量关系并体验到数学的重要和有趣”。因此，教师可以模拟生活情境来设计数学游戏，让幼儿在与他们生活紧密联系的情境中开展数学游戏。比如：为了让幼儿认识几何图形，教师设计了数学游戏“小小超市”，提供各种形状的用品和食品，让幼儿描述物品的形状，根据形状对物品进行分类，用橡皮泥制作指定形状的物品。

（二）经验前置与迁移法

在玩数学游戏前，教师可引导幼儿复习与认知游戏开展所需的关键经验，并引导他们在游戏中迁移已有经验解决数学问题，这不仅能让幼儿巩固已有经验，还能让他们在迁移经验解决问题的过程中习得新经验。经验迁移有三种情况：

1.同一个游戏情境下的经验迁移。比如在数学游戏“图形骰子翻翻乐”中，幼儿在第一次游戏中有了翻骰子说图形的经验，在第二次游戏时教师要求幼儿听指令翻图形，引导幼儿迁移已有图形经验。

2.一前一后两个游戏情境下的经验迁移。比如“分果果”和“小兔吃萝卜”这两个一前一后的数学游戏，幼儿在分水果的游戏情境中获得了分类经验，然后将它迁移到分萝卜的游戏情境中。

3.不同年龄阶段之间的经验迁移。比如小班幼儿在下学期数学游戏“吃水果”中，学会了5以内的等量集合，他们在中班上学期玩数学游戏“喂食物”时就将等量集合经验迁移到喂小猪的游戏情境中。

（三）分层指导法

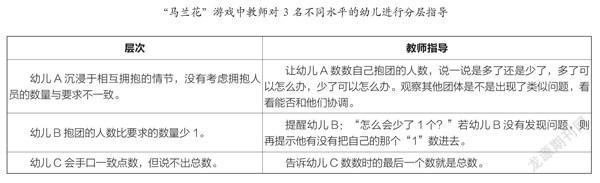
每个幼儿都是独立的个体，他们在学习过程中都会存在一些个体差异，按照自己的发展路径前进。在数学游戏中，教师应敏锐地观察、解读幼儿的个体差异，根据幼儿的发展路径对他们进行分层指导，让每名幼儿都能习得适宜自己的数学能力和经验。比如在数学游戏“马兰花”中，教师对3名不同水平的幼儿进行分层指导，促进他们形成数学关键经验（见上表）。

（四）多次反复法

数学经验和能力的习得往往需要幼儿多次反复地玩同一个或同一类数学游戏，他们在多次反复地玩游戏的过程中不仅能创新游戏玩法，还能巩固和发展数学经验和能力。

1.同一个情境下，由于玩法不同或者规则的改变，游戏可以反复进行。比如在数学游戏“图形骰子翻翻乐”中，同样的玩骰子的情境，第一次游戏可要求幼儿翻骰子说图形，第二次游戏则要求幼儿听指令翻图形。该游戏层层递进，幼儿可多次反复地进行。

2.当一种情境不能达成游戏目标时，教师可创设新的情境，在调动幼儿兴趣的同时引导他们多次反复地游戏。比如数学游戏“穿糖葫芦”，旨在让幼儿“按形状标记对图形进行归类”。在游戏规则不变的情况下，教师先创设了穿糖葫芦的情境，让幼儿通过穿糖葫芦习得按圆形、三角形、正方形归类的经验，然后又创设了穿烧烤食物的情境，让幼儿从中更好地认识物体形状的特征。

3.支持因幼儿在表达交流中流露出的需要而出现的反复游戏。游戏需要营造一个“数学交流”的学习共同体，教师应允许和鼓励每个幼儿表达自己的数学思维过程，不断提升幼儿使用数学语言的能力。当幼儿需要通过多次反复游戏才能更好地整理自己的逻辑、修正自己的思维、总结自己的经验时，教师应予以支持，为幼儿提供多次反复游戏的时间、空间和材料等。比如在玩魔法棋盘“找相同”的游戏中，一名幼儿拿出一张苹果实物卡片，另一名幼儿找出与其一样的卡片，教师问：“什么和什么一样？”刚开始游戏时，幼儿会说出游戏语：“苹果和苹果一样。”多次玩耍后，有的幼儿拿到苹果实物卡片时会说：“红色和红色一样。”拿到香蕉实物卡片时就会说：“黄色和黄色一样。”这时教师便顺势改变游戏规则，将实物卡片变成颜色卡片，提问的内容改变为：“什么颜色和什么颜色一样？”随着对游戏玩法日益熟悉，幼儿能在“好朋友”主题背景下创造新的游戏语，如：“红色和红色是好朋友，它们在一起。”“蓝色和蓝色是好朋友，它们在一起。”之后，教师根据幼儿的表现和需要改变操作材料，让幼儿拿出相匹配的实物卡片如牙膏和牙刷，并说出游戏语：牙膏和牙刷是好朋友，它们在一起。在魔法棋盘这一情境下，教师引导幼儿表达与交流，根据他们的需求改变游戏规则，让他们多次反复地进行游戏，从而习得分类、对应等数学能力和经验。