基于生灭过程的公共自行车站点车辆调度方法研究
李牧添,朱从坤
(苏州科技大学 土木工程学院,江苏 苏州 215011)
近年来,随着公共自行车系统的快速发展,公共自行车站点经常出现“无车可借、无桩可还”的现象。这严重影响了市民对公共自行车的使用体验,制约了公共自行车的进一步发展,因此合理的车辆调度尤为迫切。
在公共自行车车辆调度方面,芮一鸣等[1]以库存理论为基础,分析车辆调度的启动阈值,并结合系统特性,建立了基于用户满意度的多目标调度模型;黎文建[2]在兼顾用户满意度和运营商调度成本的同时,以时间窗惩罚值最小为目标,建立了带模糊时间窗的动态调度路径优化模型,并利用蚁群算法对模型进行求解;焦云涛等[3]提出一种以离散差分算法为基础的混合算法,用于生成公共自行车动态调度的初始方案,并根据需求预测信息和实时需求信息对初始方案进行动态调整;刘新宇等[4]以用户需求最大化和调度成本最小化为目标,建立了公共自行车车辆调度路径的优化模型,并利用遗传算法对模型进行求解,验证了模型的有效性。综上所述,目前车辆调度模型多以用户满意度最大化、调度成本最小化和调度路径最优化等为目标,利用不同算法对模型求解,最终得到不同的调度方案。
本文利用生灭过程理论分析公共自行车站点的状态概率分布特征,建立站点的状态概率模型,并根据站点的调度需求提出最佳调度时机和调度车辆数,以满足用户的借、还车需求。
1 基于生灭过程的公共自行车站点的状态概率模型
1.1 公共自行车站点排队模型
在公共自行车使用过程中,用户借、还车都要与站点上的停车桩进行交互。在每个站点,单个停车桩位都会存在满桩和空桩两种状态。为了将公共自行车站点的“借车”和“还车”两种服务放在同一个模型进行研究,将公共自行车站点看作是一个M/M/K/K的损失制排队系统[5],站点内总停车桩位数看作排队系统中的服务台数K,站点的系统容量也为K,并假设借车用户到达的时间间隔和站点的服务时间均服从负指数分布M。
1.2 基于生灭过程的站点状态概率分布模型
单个公共自行车停车桩状态变化如图1所示。当单个停车桩处于满桩状态(空闲状态)时,该停车桩可提供借车服务,但无法还车;当单个停车桩处于空桩状态(服务状态)时,该停车桩无法借车,但可以提供还车服务。结合生灭过程理论,图1中将停车桩满桩状态转变为空桩状态的过程看作是“生的过程”,把桩位从空桩状态转变为满桩状态的过程看作是“灭的过程”。
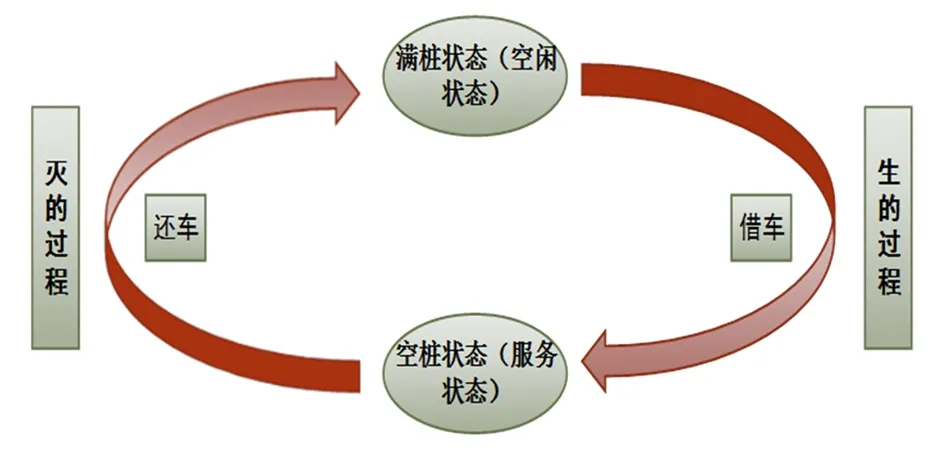
图1 单个公共自行车停车桩位状态变化图Fig.1 State change diagram of a single public bicycle parking spot
设某公共自行车站点的总桩数为K,空桩数为n(0≤n≤K),则满桩数(在桩的公共自行车数量)为K-n。对于任一时刻t,若站内空桩处于状态Sn(即站内有n个空桩),随着时间的变化,Sn存在以下4种可能[6-7]:
①在时间(t,t+Δt)内,有一位用户到达站点借车,空桩由状态Sn转移到Sn+1(n≥0)的概率为λnΔt+o(Δt),其中λn为状态Sn时的出生率。
②在时间(t,t+Δt)内,有一位用户到达站点还车,空桩由状态Sn转移到Sn-1(n≥1)的概率为μnΔt+o(Δt),其中μn为状态Sn时的死亡率。
③在时间(t,t+Δt)内,没有用户到达站点进行借、还车,站点内空桩状态没有发生转移的概率为1-λnΔt-μnΔt+o(Δt)。
④在时间(t,t+Δt)内,同时有两个或两个以上的用户在站点进行借、还车,空桩状态发生两次或两次以上转移的概率为o(Δt)。
假设在一定时段内,用户借车与还车的到达率保持不变,则站点的出生率表现为用户的借车到达率,而站点的死亡率取决于用户的还车到达率和站点内的空桩数量。站点出生率λn和死亡率μn的计算公式如下:[8]
λn=λ,n=0,1,…,K
(1)
(2)
式中:λ为平均借车速率,辆/h;μ为平均还车速率,辆/h。
站点的服务强度ρn为借车用户到达速率与服务台数量和平均服务速率乘积的比值,即
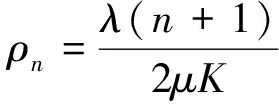
(3)
当ρn<1时,系统是稳定的。
对每个状态而言,当出生率期望值等于死亡率期望值时,系统达到状态平衡[9],即对于任意状态Sn,出生率期望值为E=μnPn+λnPn(Pn为公共自行车站点处于n个空桩状态的概率),死亡率期望值为E′=λn-1Pn-1+μn+1Pn+1。当E=E′时,系统达到状态平衡,有:
μnPn+λnPn=
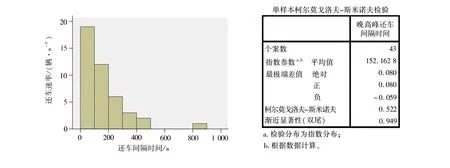
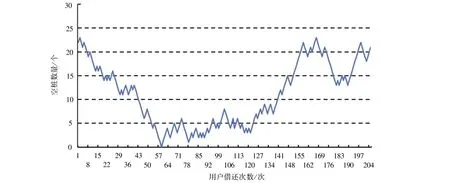
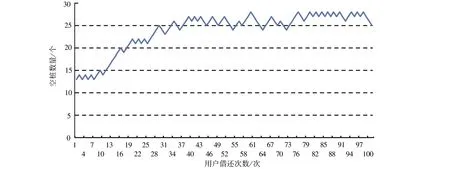
λn-1Pn-1+μn+1Pn+1(1≤n (4) 对于状态S0,有μ1P1=λ0P0 (5) 对于状态SK,有λK-1PK-1=μKPK (6) 式(4)~式(6)称为生灭过程的哥尔莫可尔夫方程[10],联解可得: (7) 站点内空桩的期望值E空、满桩的期望值E满计算公式如下: (8) E满=K-E空 (9) 以苏州市轨交滨河路公共自行车站点早、晚高峰期为例进行状态概率分析,车辆实时借、还数据由永安行苏州分公司提供。该站点总桩位数K=30,分析时段为2019年6月12日的早高峰(7:00—9:00)与晚高峰(17:00—19:00)。这两个时段内车辆借、还速率如表1所示。 运用SPSS Statistics软件对以“秒”为单位进行统计的轨交滨河路公共自行车站点早、晚高峰期的借车间隔时间和还车间隔时间进行分布检验,结果如图2~图5所示。 图2~图5的检验结果显示,该站点借、还车间隔时间分布的渐进显著性均大于临界值P=0.05,表明该站点在早、晚高峰时段借还车间隔时 表1 轨交滨河路公共自行车站点车辆借还速率Table 1 Vehicle loan and return rate at the public bicycle station on Binhe Road of rail transit 间均服从负指数分布。 将表1数据代入式(7)~式(9),可得该站点在早、晚高峰两个时段的状态概率分布Pn、服务强度ρn和空(满)桩期望,如表2所示。 利用实际借、还车数据,还可绘出该站点早、晚高峰时段的空桩数量变化曲线,如图6所示。 图2 早高峰借车间隔时间分布及检验结果Fig.2 The distribution of the car-borrowing interval in the morning rush hour and test results 图3 早高峰还车间隔时间分布及检验结果Fig.3 The distribution of the time interval between returning vehicles in the morning rush hour and test results 图4 晚高峰借车间隔时间分布及检验结果Fig.4 The distribution of the car-borrowing interval in the evening rush hour and test results 图5 晚高峰还车间隔时间分布及检验结果Fig.5 The distribution of the time interval between returning vehicles in the evening rush hour and test results 表2 苏州市轨交滨河路公共自行车站点部分状态的统计数据Table 2 Statistical data of part of the state of the public bicycle station on Binhe Road of Suzhou Rail Transit 由表2可知,早高峰时段该站点处于S0状态(系统内有0个空桩)的概率要远大于S30状态(系统内有30个空桩)的概率,说明该站点在早高峰时段大概率会出现“无桩可还”现象;晚高峰时段该站点处于S30状态的概率要大于S0状态的概率,说明该站点在晚高峰时段大概率会出现“无车可借”现象。这一结论与图6所表现出的空桩数量变化规律一致,表明该站点在早高峰时段有车辆调出需求,在晚高峰时段有车辆调入需求。 针对苏州市轨交滨河路公共自行车站点在早高峰易出现“无桩可还”、晚高峰易出现“无车可借”现象,以早、晚高峰期间的空桩期望E空为参考,确定车辆调度的启动阈值。即早高峰期间,当站点内仅存1.73个空桩时,应该对该站点进行车辆调出;晚高峰期间,在站点有21.17个空桩时,应该对站点进行车辆调入。考虑到车辆调度所花费的时间损耗,将车辆调度启动阈值适当提高,即在站点只有2~4个空桩时对站点实施车辆的调出,在站点有21~23个空桩时对站点实施车辆的调入。 a 早高峰 b 晚高峰图6 苏州市轨交滨河路公共自行车站点早、晚高峰空桩数变化曲线图Fig.6 The change curve of the number of empty piles in the morning and evening peak hours at the public bicycle station of Binhe Road, Suzhou Rail Transit 在早高峰期间站点调出车辆时,还需同时考虑避免出现“无车可借”的现象。由公式(7)可知,在站点的平均借车速率与平均还车速率不变的情况下,“无车可借”的概率PK随K值而变化。早高峰时段站点在不同规模下处于SK状态的概率PK的部分结果如表3所示。 表3 不同规模下站点在早高峰处于SK状态的概率 若能接受“无车可借”现象的概率为1%左右,由表3可知,K=7时,P7=0.010 7(即“无车可借”的概率为1.07%)符合要求。即车辆调度人员在早高峰期间调度车辆时,应保证站点内至少有7辆公共自行车。 同理可确定晚高峰的车辆调度数量。利用公式(7)计算晚高峰时段站点在不同规模下处于S0状态概率P0,部分结果如表4所示。 表4 不同规模下站点在晚高峰处于S0状态的概率 若能接受“无桩可还”现象的概率为1%左右,由表4可知,当K=11时,P0=0.010 8和K=12时,P0=0.009 2均符合要求,只是K=12时,出现满桩的概率要低一些。即车辆调度人员在晚高峰期间调度车辆时,应保证站点内至少有11个或12个空桩。 根据生灭过程和排队论的相关理论研究公共自行车站点车辆调度方法,建立公共自行车站点状态概率分布模型,推导出站点的状态概率分布、服务强度、空桩期望等计算公式;在站点服务强度 的前提下,利用站点状态概率分布确定站点的调度需求,以站点空桩期望作为参考制定车辆调度的启动阈值,讨论站点合理的车辆配置数量,为公共自行车站点车辆调度方案的制定提供定量依据。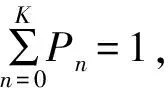
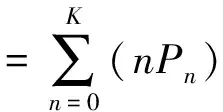
2 典型站点状态分析
2.1 站点车辆借、还间隔时间分布检验
2.2 站点状态特征分析
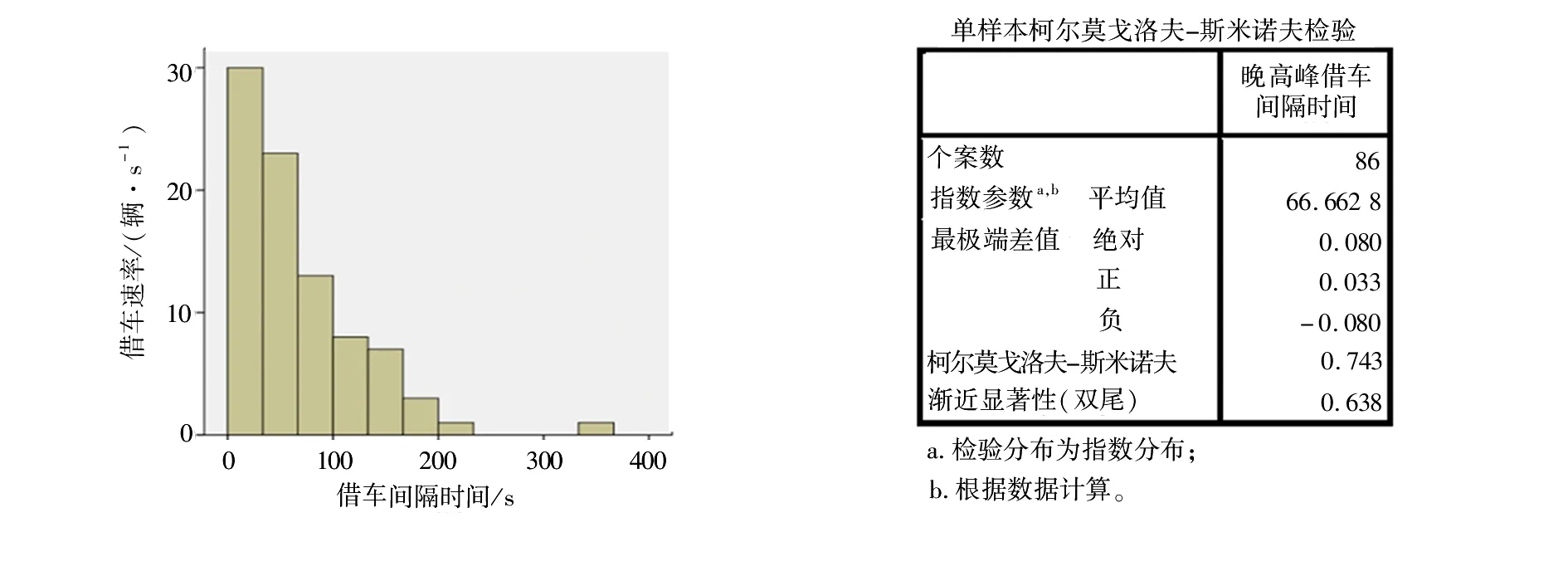

3 站点车辆调度方法
3.1 站点车辆调度阈值
3.2 站点车辆调度数量


4 结语

