函数凹凸性视角下的双变量压轴题的探究
广东省佛山市乐从中学(528315) 林国红
函数凹凸性是函数的一种特殊特征,近年来,以函数凹凸性为背景的题目屡见不鲜,这些试题情景新颖,能考查学生的创新能力和潜在的数学素质,常作为压轴题出现.虽然在高中课本中没有这方面的内容,但高中教师若能多了解一些函数凹凸性的相关理论知识,可以“登高望远”,便于找到问题的本质内涵,确定解题方向,寻找简捷的解题途径.
本文从函数凹凸性的视角,对一些双变量的函数压轴题进行探究,揭示试题的命题背景与内涵.
一、函数的凹凸性及常用性质
1.函数凹凸性的定义

2.凹凸函数的常用性质
(1)函数凹凸性的判定定理设f(x)在[a,b]上连续,在(a,b)内具有一阶和二阶导数,那么:若f(x)在(a,b)内有f′′(x)>0,则f(x)在[a,b]上是下凸函数;若f(x)在(a,b)内有f′′(x)<0,则f(x)在[a,b]上是上凸函数.

证明如图1,设点A,B,M的坐标为(x1,0),(x2,0),则点D,C的坐标为(x1,f(x1)),(x2,f(x2)).直线与函数y=f(x)的图象交于点N,过N作y=f(x)的切线l,由于f(x)是[a,b] 上连续的下凸函数,故切线l在曲线y=f(x)的下方,设切线l分别交AD,BC于F,E两点,则MN为梯形ABEF的中位线.
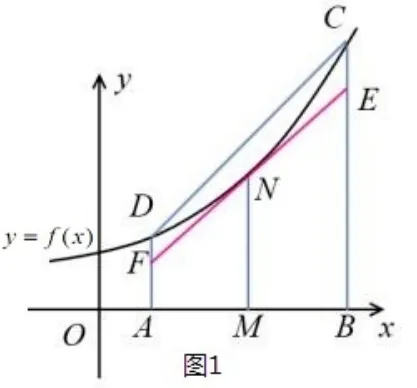

评注若f(x)是[a,b]上连续的上凸函数,则上述不等式的不等号反向.
(3) 切线不等式若f(x) 在区间I为下凸函数,则对 于∀x0∈ I,有f(x) ≥f′(x0)(x −x0) +f(x0);若f(x) 在区间I为上凸函数,则对于∀x0∈I,有f(x) ≤f′(x0)(x −x0)+f(x0).
高中阶段两个常见的切线不等式:ex≥x+1(x≥0)与lnx≤x −1(x>0).
二、函数凹凸性在极值点偏移中的应用
1.极值点偏移的判定定理
定理1 已知函数y=f(x)在区间(a,b)上连续,且有(a,b) 内只有一个极值点x0.若对于a


2.典型例题

例2 (2016 年高考全国Ⅰ卷理科第21 题) 已知函数f(x)=(x −2)ex+a(x −1)2有两个零点.
(1)求a的取值范围;
(2)设x1,x2是f(x)的两个零点,证明:x1+x2<2.
解析(1)a的取值范围为(0,+∞),过程略.

评注极值点偏移作为函数变化过程中的一种重要现象,一直颇受命题人的喜爱.极值点偏移问题的解法一般是构造偏移函数法或比值代换法,虽然这些方法可以解决极值点偏移问题,但是较难从本质上判定任意一个函数是否具有偏移现象,左偏还是右偏.哈达玛不等式是命制极值点偏移问题的一个常用理论背景,试题通过构造具有凹凸性的函数,这样就可以从理论上保证极值点偏移的出现.
三、函数凹凸性中切线不等式的应用
例4 同例1.
解析由例1 可知,问题(2)等价于:已知f(x1)=f(x2),证明:2 设0 图2 由于f(x)在点(e,0)处的切线方程为y=−x+e,设切线与y=m交于点C(xc,m),则xc=−m+e.由图可知,0 例5 (2020 年合肥三诊理科第21 题)已知函数f(x)=(e 为自然对数的底数). (1)求函数f(x)的零点x0,以及曲线y=f(x)在x=x0处的切线方程; (2)设方程f(x)=m(m >0)有两个实数根x1,x2,求证:|x1−x2|<2− 图3 评注显然,例4,例5 中问题(2)的命题背景是立足于函数凹凸性中的切线放缩,解题思路是通过切线与直线y=m的交点横坐标来估计出两个零点和(或差)的范围.需要注意的是,在例5 中如果选择曲线y=f(x)在x=1 处的切线方程为y=(x −1)来放缩,则得不到想要的结果,因为当x ∈(0,1)时,切线y=(x −1)并不在曲线y=f(x)的上方(如图4). 图4 例6 (2020 年高考天津卷第20 题) 已知函数f(x)=x3+klnx(k ∈R),f′(x)为f(x)的导函数. 例7 (2013 年高考陕西卷理科第21 题) 已知函数f(x)=ex,x ∈R. (1)若直线y=kx+1 与y=f(x)的反函数的图象相切,求实数k的值; (2)设x >0,讨论曲线y=f(x)与曲线y=mx2(m >0)公共点的个数; 以函数凹凸性为命题背景的试题还有很多,通过以上几道例题,不难体会函数凹凸性等相关知识的丰富性,这也表明:高等数学的相关理论是命制一些具有创新力与区分度的高考试题的重要来源.虽然函数凹凸性不属于高中数学的内容,但是掌握相关知识,能帮助教师与学生找开思维视角,养成对试题背后的内在关系分析与思考习惯. 近年来,高考的命题者通过挖掘高等数学中的一些素材来命制高考试题,此类试题也逐渐引起老师们的关注.但这并不意味着要将过多的高等数学知识下放到中学里来,加重中学的负担.应该是教师能站在高观点的角度看待问题,将研究的问题引向深入,探索隐藏在题目背后的奥秘,挖掘题目的真正内涵,能够找到解决这个问题与解决其它问题在思维上的共性.这样我们才能领会到试题命制的深刻背景,才能引领学生跳出题海,真正做到触类旁通,举一反三,更好地指导中学的数学教学.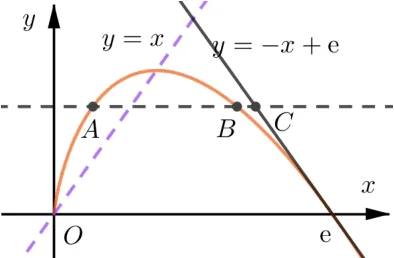

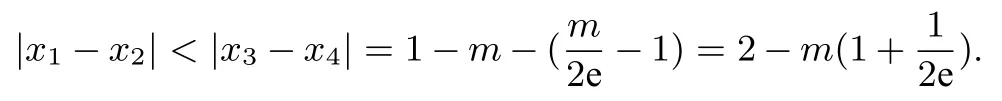


四、哈达玛不等式的应用

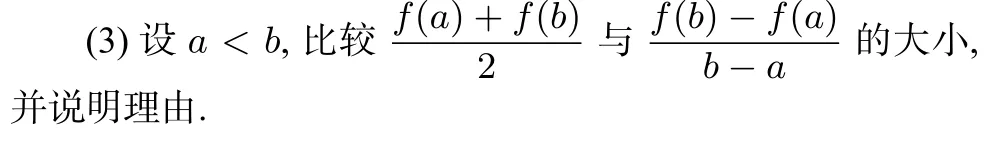

五、结束语

