两个尺规作图问题初探

广东省佛山市顺德区北滘中学(528311) 雷火华

本文探讨2 个尺规作图问题:

①过圆外一点,作直线与圆相切.

②过圆外两点(这两点与圆心不共线),作圆与已知圆相切.

希望能起到抛砖引玉的作用,让更多的尺规作图问题得到关注讨论.

1 过圆O 外一点A 作与圆O 相切的直线问题

已知:⊙O以及⊙O外一点A,求作直线过点A且与⊙O相切.

作法:①连结AO;②取线段AO的中点B;③以点B为圆心,BA长为半径作⊙B,交⊙O于点C、D;④作直线AC、AD;则,直线AC、AD为所求.

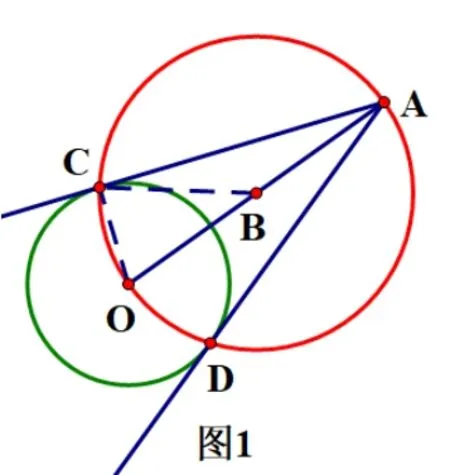
如图1,连结BC、OC,∵BC=BO,∴∠BOC=∠BCO,同理可得∠BCA=∠BAC,∴∠OCA=∠BCO+∠BCA=,∴AC与⊙O相切于点C.故,AC为所求.

2 过圆A 外两点C、D(C、D、A 三点不共线)作与圆A 相切的圆问题

已知:⊙A以及⊙A外两点C,D(C、D、A三点不共线),求作一圆过C,D两点且与⊙A相切.

作法:①连结AC,取AC的中点E;②作AC的垂直平分线EG;③取CD的中点F;④作CD的垂直平分线FG,交EG于点G;⑤以G为圆心,GA长为半径作圆G,交⊙A于H、I两点;⑥作直线HI,交直线CD于点J;⑦连结AJ,取AJ的中点K;⑧以K为圆心,KA长为半径作圆K,交⊙A于点L;⑨连结CL,取CL的中点M;⑩作线段CL的垂直平分线MN,交FG于点N;⑪以N为圆心,NL长为半径作圆N;则,⊙N为所求.

如图2,图3,⊙N与⊙A有外切、内切两种情况.

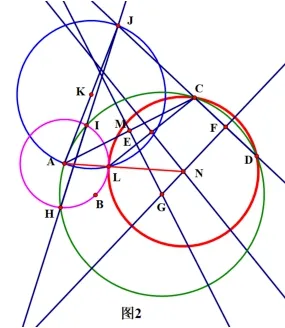
图2

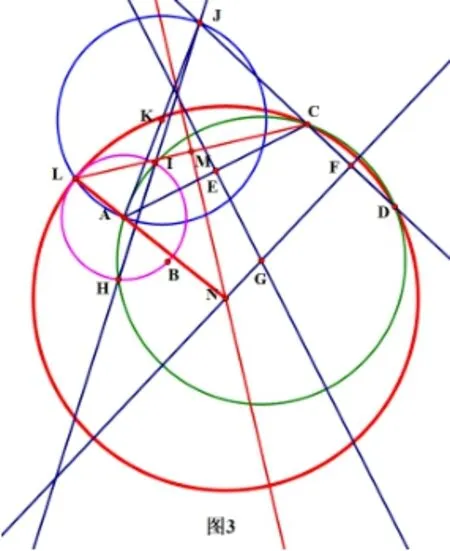
图3

证明:如图4,连结JL;∵AJ为⊙K的直径,

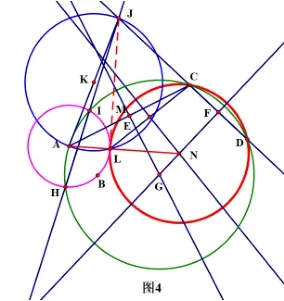
图4

由①④得:∠ALN=∠ALJ+∠JLN=π,∴A、L、N三点共线,又∵点L既在⊙A上,又在⊙N上,∴⊙N与⊙A相切于点L,又∵⊙N过C,D两点,故⊙N为所求.

当圆心A与圆外两点C、D共线时,又如何呢? 有空,大家研究研究.

空闲时,笔者常常点开“几何画板”,设计一些曲线、图形,拖动一些点,设计一些点的变化,而产生一些新的、有特别意义的曲线,一来可以让自己欣赏变化曲线的优美,二来也进一步研究一些自己以前不知道的数学结论,借助于“几何画板”工具,让自己在尺规作图上有不少的数学发现.

笔者认为,借助“几何画板”工具进行尺规作图教学,既能让学生欣赏变化曲线的优美性,激发学生的学习兴趣,又有助于培养学生发现问题、解决问题的能力,更有助于培养学生的想象力和创造力.