基于KL-E 的地质力学模型参数反演及应用
覃建华,杨琨,丁艺,张博宁,唐慧莹
1.中国石油新疆油田分公司勘探开发研究院,新疆 克拉玛依 834000;2.中国石油新疆油田分公司开发公司,新疆 克拉玛依 834000;3.成都北方石油勘探开发技术有限公司,四川 成都 610051;4.油气藏地质及开发工程国家重点实验室·西南石油大学,四川 成都610500
引言
地应力的分布特征对于了解油气运移、钻井方案及水力压裂设计、提出油气藏生产的优化设计方案具有重要意义[1-4]。要准确预测地应力值以及三维地应力场的分布,就有必要明确储层的地质力学性质、几何特征及边界条件[5]。
目前,已有多种方法可用于储层地应力的确定,例如,井壁崩塌法[6]、水力压裂法[7]、声发射法(AE)[8]以及震源分析法[9-10]等。此外,还可以根据经验公式利用测井数据计算地应力[11]。岩芯分析是目前确定应力大小最直接、可靠的方法[12],通常被作为硬数据对其他模型进行标定。但受费用、测试样品的干扰性及采样点位置等影响,使得通过岩芯分析来描述整个储层特征具有较大的挑战性[13]。因此,有必要采用其他方法来获得整个地应力场的应力分布。
侧压系数法假设地应力水平分量与垂直分量之比是常数,同时考虑应力随深度的变化,但该方法得到的应力分布评价较为粗略[14-15]。Gens 等[16]和Miranda 等[17]在隧道工程中引入了反分析方法。反分析方法是构建关键参数(边界参数、弹性模量)的一个函数(线性或非线性)来表示整个区域内的位移或应力分布,调整方程的系数直到与参考值相符[18-19]。该方法只适用于储层性质相对均匀的薄层,不适用于非均质性较强,地质条件复杂的地层。Ito 等[20]提出了一种基于有限元计算的地质模型参数反演方法,该方法将应力场视为上覆岩层应力和构造应变诱导应力的叠加。张社荣等[21]通过在线性回归方程中考虑不同应力分量之间的相互作用,改进了该方法。近年来,一些更复杂的反演算法被应用到了岩石力学问题当中。Nguyen 和Nestorovi[22]以隧道引起的沉降和水平位移为参考,采用非线性卡尔曼滤波算法对隧道地质力学模型中的地质材料参数进行校准。Li 等[23]提出了一种结合贝叶斯方法与多向量输出算法(B–MSVM)的方法来反演地应力模型的杨氏模量和侧压系数。Zhuang 等[24]采用多策略人工鱼群优化向量回归算法,对隧道工程中围岩力学参数进行反算。然而,这种方法只能提供应力分布,且地质力学参数场没有调整。上述方法在一定条件下对应力场计算具有良好的适用性,但是并不对地质力学参数场进行更新。地震数据是解释弹性参数(杨氏模量和泊松比)的可靠依据[25]。对于无法获得可靠三维地震资料的情况,通常采用基于一维解释资料的随机算法(克里金法,高斯序贯模拟)生成属性场。在给定随机参数和硬数据(测井或解释数据)的情况下,可以生成任意数量的实现,但由于网格数量通常较大,人为调整每个网格的值非常困难[12]。Gao 等[26]采用逐次线性估计(SLE)算法对隧道开挖问题的单元地质力学参数场进行了统计校正,但这种方法的有效性受网格的质量及数量等影响较大。为了加速对随机场的同化,Karhunen–Loève 展开(KL-E)已被多次用于渗流问题的分析[27-29]。KL-E 利用特征函数和随机变量的一系列线性组合产生不确定参数场,可以将属性模型的输入变量从数千个基于单元的属性减少为一组数量较少的一维随机变量,大幅度提高计算效率。本文将KL-E 算法用于地质力学参数场的生成,以提高模型参数场的同化效率。
本文提出一个序贯地质力学模型参数同化算法,同时对地质力学参数场和模型边界条件进行调整。该方法利用Matlab 优化工具箱中的全局优化算法——遗传算法(Genetic Algorithm,GA)实现随机变量的同化,同时利用局部优化算法模式搜索(Pattern Search,PS)进行边界条件的反演。首先,采用KL E 生成地质力学参数随机场;然后,通过两步序贯方法分别对边界条件和参数场进行同化。目前,计算中只考虑了杨氏模量属性场和水平应变边界条件。文中给出的测试算例与四川盆地页岩气的实例均论证了该方法的有效性。计算结果表明,边界条件的同化相对容易,而属性场的收敛是相对缓慢和困难的。但通过对地质力学参数场进行同化计算,可进一步提高模型计算应力与一维应力参考值的吻合度,从而提高整个地质力学模型的可靠性。
1 地质背景
本文分别用PS 和GA 对边界条件和地质力学参数场进行同化。目前,只考虑杨氏模量的场分布,其分布由KL-E 生成。考虑到一维解释应力或实测应力位置通常也有测井资料可用于解释沿井眼的杨氏模量,本文在最后的实例计算中进一步采用条件KL-E 算法,即在采用KL-E 算法的同时,满足参考点参数值不变的前提条件,既能生成满足统计参数的随机场,又能保持有硬数据的位置参数值不变。目前,只进行二维地质力学参数场的同化。
1.1 地质力学参数随机场的生成
假设储层地质力学性质的分布满足高斯分布,就可利用KL-E 描述杨氏模量场。如果随机场满足高斯分布,则参数场分布可以分解为两部分

式中:x=(x1,x2)—某点坐标,m;
)—随机场的平均值,单位与变量单位一致;
Y′(x)—随机场的扰动或空间波动,单位与变量单位一致。
函数Y(x) 的协方差矩阵CY中关于位置x,y的协方值写为CY(x,y),该函数有界、对称且正定。CY(x,y)可以扩展为
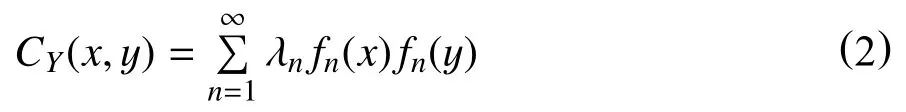
式中:
CY(x,y)—关于位置x,y 的协方值,单位为变量单位的平方;
y=(y1,y2)—另一点空间坐标,m;
λn—协方差矩阵的特征值,为正数,无因次;
fn(x),fn(y)—相互正交的协方差矩阵的特征函数,与待求变量单位一致。
特征值与特征函数之间满足

式中:fi—特征向量。
本文采用的协方差计算公式为

式中:
σ2—待求变量的方差,单位为待求变量单位的平方;
η1—平行于x1方向的变量分布相关长度,m;
η2—平行于x2方向的变量分布相关长度,m。
通过将协方差矩阵分解为特征值和特征函数的组合,可以通过式(5)生成随机场

式中:ξn—满足方差为1、均值为0 正态分布的随机数,无因次。
由于特征值的急剧衰减,只需使用式(5)中部分随机变量逼近随机场,这将大大节省计算时间。截断项为N的KL-E 可用于近似参数场分布
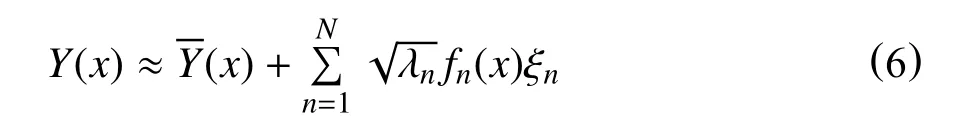
其中,特征值按最大值到最小值排列。截断项个数的确定采用保留特征值之和大于所有特征值之和80%的原则[29]。
为了考虑同化前获得的硬数据,本文采用条件KL-E。条件KL-E 可以在给定位置的硬数据不变的情况下产生随机场。本文采用了与Xue 等[30]相同的算法。
假设共有nY个测量点(给定硬数据所在位置),测量值分别为Y1(x1),Y2(x2),···,YnY(xnY);坐标为x1,x2,···,xnY。条件克里金平均值和协方差函数可以计算如下

式中:上标c—条件;
µi(x)—每个测量点的权重函数,无因次,根据克里金公式计算为

确定后即可根据式(8)计算协方差矩阵并根据式(3)计算特征值与特征函数。最终条件随机场表达式为

(x)—条件协方差矩阵特征函数,与变量单位一致。
为了减少计算时间,特征值和特征函数只在第一次实现计算一次,其他现实可直接采用。由于岩土力学性质应为正,因此,采用Y(x) >0 约束杨氏模量参数场取值。利用条件KL-E 进行参数场同化,只需调整随机参数ξn的值,而非每个网格的参数值,从而大大节省了同化参数的数量,提高了模型同化和收敛的效率。
1.2 地质力学有限元模型
利用有限元模拟建立地质力学模型并进行计算。本文测试算例忽略了孔隙弹性效应,假定孔隙压力为常数且等于0,而在现场实例研究中将考虑孔隙弹性效应和孔隙压力的非均质性。
为避免有限元模拟时可能出现的边界效应,先对目标储层网格进行扩展[31]。模型由上层(绿色)、侧部(白色)、下层(红色)和目标层(深蓝色)等4 个区域组成(图1)。每个区域的网格如图2 所示,油藏网格中的随机颜色代表不同的物质类型。由于ABAQUS 中使用的颜色是有限的,因此,某些具有不同属性的网格将以相同的颜色显示。本文只考虑目标储层的应力和地质力学性质分布,其余区域用于消除模型边界附近的应力集中。

图1 不同区域示意图Fig.1 Schematic of different regions

图2 不同区域网格Fig.2 The grid of different regions
有限元模型边界条件施加:水平方向施加法向应变边界条件(εxx、εyy—x,y 方向的应变量,即图3中x,y 方向的边界条件)。由于所建模型没有扩展到地表以减少网格数,因此,在模型顶部施加额外的面力(σzz,图3 中的垂向边界条件)以表征上层岩石的重力作用,同时固定另外3 个表面的法向位移(图3)。

图3 有限元模拟中使用的边界条件Fig.3 The boundary conditions used in the FEM simulation
在同化过程中,上层、侧部和下层网格的地质力学属性参数保持不变,仅目标储层中每个网格的性质以及边界条件随着计算过程而改变,目标层中网格属性根据1.1 中介绍的条件KL–E 算法获得。本文利用内部编写的Python 脚本实现ABAQUS 有限元模型的网格属性自动赋值和后台运行。
1.3 序贯两步同化算法
本文提出一个序贯两步同化算法:首先,采用模式搜索(PS)算法对边界条件(xx和yy)进行同化;随后,利用遗传算法(GA)实现岩土力学参数(杨氏模量)的同化。若需要进一步提高模型与参考值的匹配程度,可进行另一轮反演,直到满足收敛准则为止。详细工作流程如图4 所示。

图4 序贯两步同化过程示意图Fig.4 Schematic of the sequentially two-step assimilation procedure
优化的目标是找到边界条件或地质参数的值,以便将观测位置处的模拟应力和解释应力之间的差降到最小。目标函数F(x)定义为
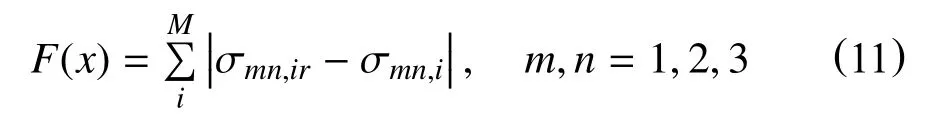
式中:
σmn,ir—通过一维地质力学分析解释得到的地应力值,MPa;
σmn,i—三维地质力学模型计算的应力,MPa;
M—参考点数量,个。
水平应变边界条件范围可通过式(12)估算[32]
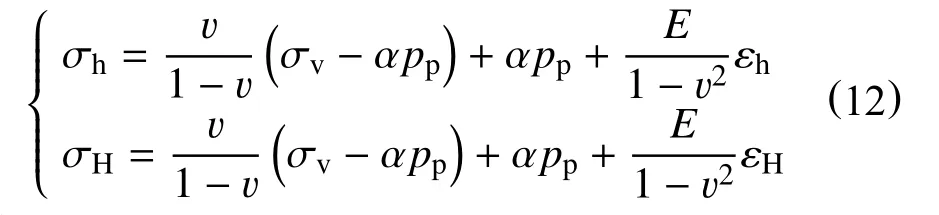
式中:
σh—最小主应力,MPa;
v—泊松比,无因次;
σv—垂向应力,MPa;
α—比奥系数,无因次;
pp—孔隙压力,MPa;
E—杨氏模量,GPa;
εh—最小水平应变,无因次;
εH—最大水平应变,无因次;
σH—最大主应力,MPa。
随机场生成需要的均值、方差与相关长度等参数从参考点的解释数据中获得,KL-E 算法中随机变量取值在[-2,2]。
2 结果与讨论
2.1 测试算例
针对测试算例,应用上述序贯两步同化算法反演杨氏模量参数场和水平应变边界条件。测试算例中,目标储层网格数为20×20×1,网格尺寸为5 m×5 m×10 m。上、下层网格厚度均为100 m,网格厚度从目标储层厚度以1.5 倍的比例递增。整个模型网格数为9 216(图2)。固定4 个网格的杨氏模量参数:(5,50),(50,5),(50,100),(100,50),假设为参考测量点。采用条件KL-E 算法生成杨氏模量的随机场。部分模型关键参数如表1 所示,边界条件如表2 所示。这些参数从实际油藏模型中提取,在测试模型中,使用了更显著的方差与更短的相关长度以加强地质力学属性场的非均质性。假设杨氏模量属性场沿x与y 方向的相关长度均为100 m。地质力学参数随机场的协方差矩阵中,前20 个特征值的总和超过了所有特征值和的85%,因此,在后续的随机场生成过程中将只对前20 个特征向量对应的随机数进行同化调整。设置遗传算法每一代人口数为20,收敛条件为连续两代的平均目标函数值差异小于5%。

表1 测试算例属性参数Tab.1 Property values for the synthetic case

表2 测试算例模型边界条件Tab.2 Boundary conditions for the synthetic case
该测试算例将进行两次同化计算,即进行两轮边界应变和杨氏模量场的序贯同化。测试算例预设参数及各步骤的结果分别记录在表3 与表4 中。杨氏模量参考场、初始杨氏模量和每一步的杨氏模量场如图5 所示,对应的应力场如图6∼图9 所示。本文定义张拉应力为正。
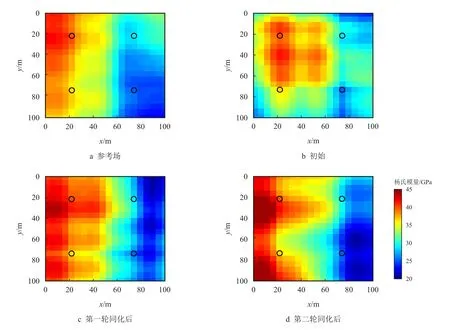
图5 杨氏模量场同化过程Fig.5 The assimilation process of Young′s modulus field

图6 参考场下地应力分布Fig.6 Distribution of in-situ stresses of reference field
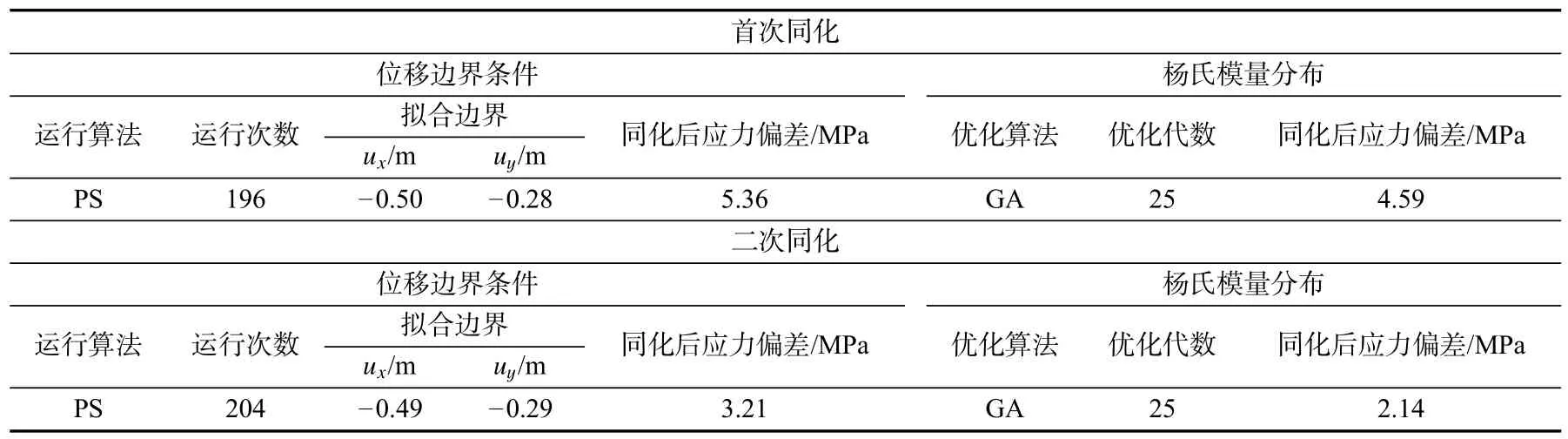
表4 测试算例计算结果Tab.4 Results of synthetic case
根据数值计算结果,经过25 代遗传算法的同化,目标值的变化基本停止。因此,在进行场同化时设定遗传算法在经过25 代计算后停止。在进行边界条件的同化时,本文设定当两次迭代的相对差值小于1%时,PS 算法停止。
表3 表明,利用序贯两步同化程序,可以有效地同化地质力学模型的边界条件和目标值。此外,边界条件的拟合速度快、精度高,表明边界条件与地应力具有很强的相关性。同时,首次拟合得到的目标函数值同化程度最高,第二次拟合对目标函数值的改变相对较小。

表3 测试算例预设参数Tab.3 Initial guess for the synthetic case
图5 为杨氏模量场随同化过程进行的演化过程。由于已知4 参考点杨氏模量值,初始实现能够部分获取空间杨氏模量分布趋势,但仍与参考场有较大差别,随着同化过程的进行,杨氏模量场分布与参考场不断接近,即使在无参考点的区域仍然能够捕捉到大部分场分布信息。图6 为利用参考杨氏模量场与边界条件计算得到的x方向与y 方向总应力分布,从图中可以看出,杨氏模量较大的区域对应压应力较大,应力分布趋势受杨氏模量分布影响明显。图7 为初始杨氏模量场与边界条件下的地应力分布,可以看到,其分布与参考场有较大分别。图8与图9 分别为第一轮与第二轮同化后应力分布,可以看到,当完成第一轮同化后,应力分布与参考场已较为接近。

图7 初始场地应力分布Fig.7 Distribution of in-situ stresses of the initial field
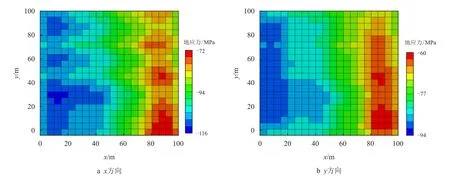
图8 第一轮同化后地应力分布Fig.8 Distribution of in-situ stresses after the first two-step assimilation
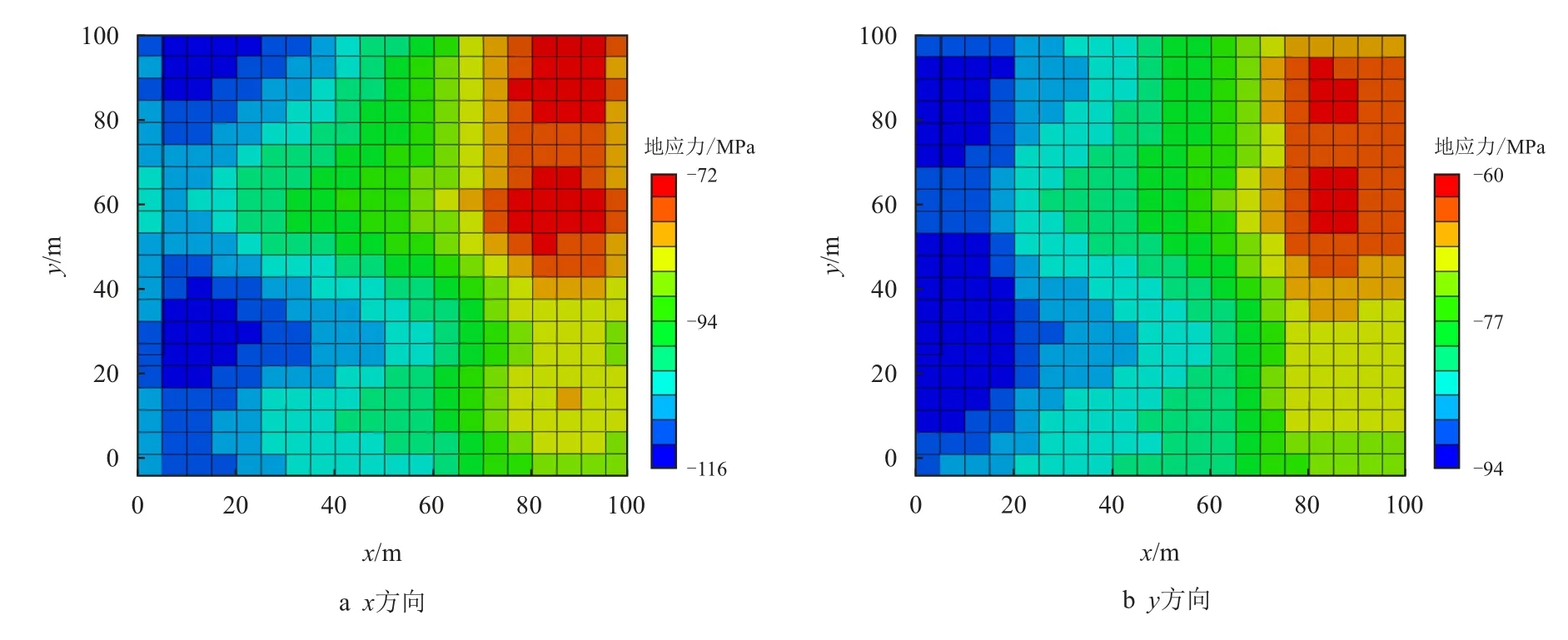
图9 第二轮同化后地应力分布Fig.9 Distribution of in-situ stresses after the second two-step assimilation
由图5∼图9 可以看出,同化杨氏模量场和应力场都能捕捉参考场的趋势和主要特征。与随机生成的初始场相比,同化后的模型具有与参考场更为相似的特征,在遗传算法中,通过多轮迭代或增加每一代的种群数量,可以进一步提高算法的精度,但同时也会增加计算时间。
2.2 实例研究
本文实例研究对象为四川盆地龙马溪组某页岩气井区。首先,利用测井、室内实验、水力压裂以及钻井等资料,对4 口水平压裂井(图10)进行了一维地质力学分析,获得了沿井轨迹的地质力学参数(杨氏模量、泊松比以及岩石硬度)和三向主应力(Sxx,Syy,Szz)。

图10 实际算例网格Fig.10 Grids of the practical case
三维地质力学模型与测试算例相似,地质力学模型包括目标储层、侧部、上部和下部地层。模型尺度为2 800 m×2 800 m×10 m,单元尺度为dx=100 m,dy=100 m,dz=10 m。网格顶部位于地表以下1 000 m处,网格底部位于海拔-5 000 m处,由于本文仅考虑二维随机场的同化,因此,选择生产潜力较大的层作为目标层,原始地质模型中主力产层包含5 层细网格,这里只对其中物性最好(渗透率与孔隙度较高)的一层网格层进行属性场反演。目标层共有8 个网格与井径交叉,将沿井轨迹与交叉网格相交部分的一维解释值进行平均获得网格平均值(图11a),在这8 个网格处固定地质力学参数,且认定为应力参考点,参考点网格编号如图11b 所示。
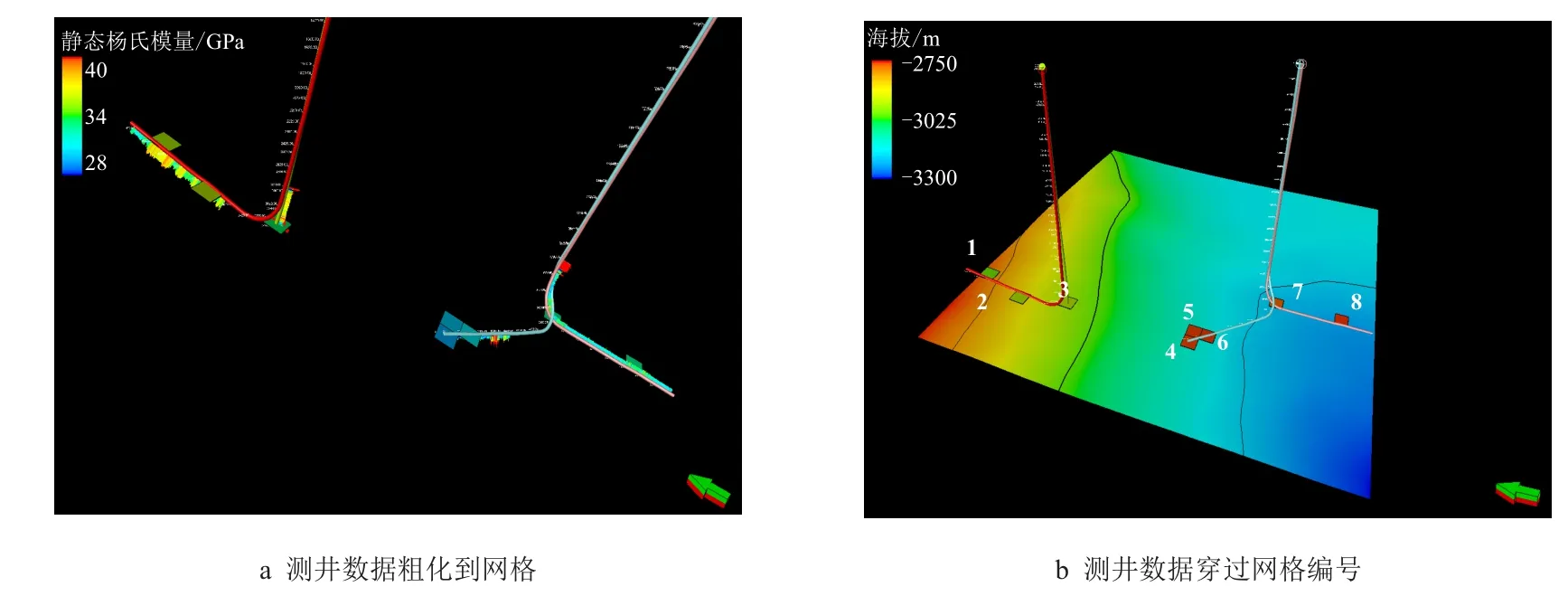
图11 测井数据在网格中的分布Fig.11 The distribution of logging data in grids
表5 列出了每个区域的材料特性,其中,杨氏模量与泊松比分布在x与y 方向的相关长度均为1 000 m。需要通过匹配观测网格中的垂直应力来调整上层岩石的密度(图12),从图中可以看出,从一维分析得到的解释垂直应力和计算垂直应力较为接近,各点编号在图11 中标出,拟合后上层岩石密度为2.55 kg/m3。由于地层实际情况与地质力学模型存在差异,解释和计算的垂直应力之间仍存在不同,但相对差异较小。

图12 垂向应力解释值与计算值对比Fig.12 Comparison of veritcal stress in interperted and calculated results
利用8 个参考点的一维解释值可以计算杨氏模量和泊松比的均值、方差和相关长度,实际算例不同区域参数如表5 所示。

表5 各区域材料特性Tab.5 Material properties in each region
研究区为高压气藏,压力系数大于1.8。根据区块多口直井的试压资料,观察到压力系数与深度之间存在较好的相关性,因此,在本算例中直接根据实际的地层深度来计算孔隙压力(图13),计算公式如式(13)所示。

图13 目的层孔隙压力分布Fig.13 The distribution of pore pressure in target reservoir layer

式中:h—垂深,m;g—重力加速度,g=9.8 m/s2。
根据水平井的水力压裂和成像测井以及微地震资料得出,最小水平应力近似平行于y轴,因此,假定主应力方向沿x,y 和z轴。目标函数,即解释应力和计算应力之间的差为
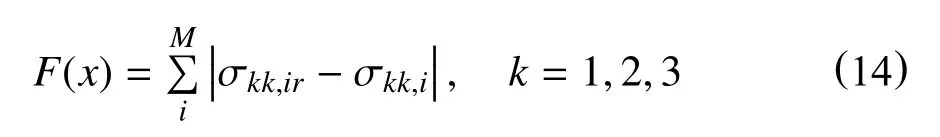
本算例中,参考点数量为8 个。利用式(12)估计边界条件的初始猜测,并用条件KL-E 生成在固定参考点属性值的杨氏模量场。表6 为实际算例的预设参数,表7 为同化过程中的计算结果及优化算法选取参数。由表7 可以看出,第一轮两步同化可以有效降低目标值,而第二轮同化后目标值变化不大,该结论与测试算例结论一致。与测试算例不同的是,实际算例优化后的最终目标值仍然较大。该现象可以从以下几个方面解释。首先,解释的一维地质力学性质和应力可能与实际值不同。此外,密度分布、泊松比和地质模型的几何形状也可能对算法的准确性产生影响。同时,从8 个点得到的随机参数可能不足以反映真实场的特征。由于观测到目标值显著降低,计算结果仍然证明了该方法在实际算例中的有效性。

表6 实际算例预设参数Tab.6 Initial guess of practical case
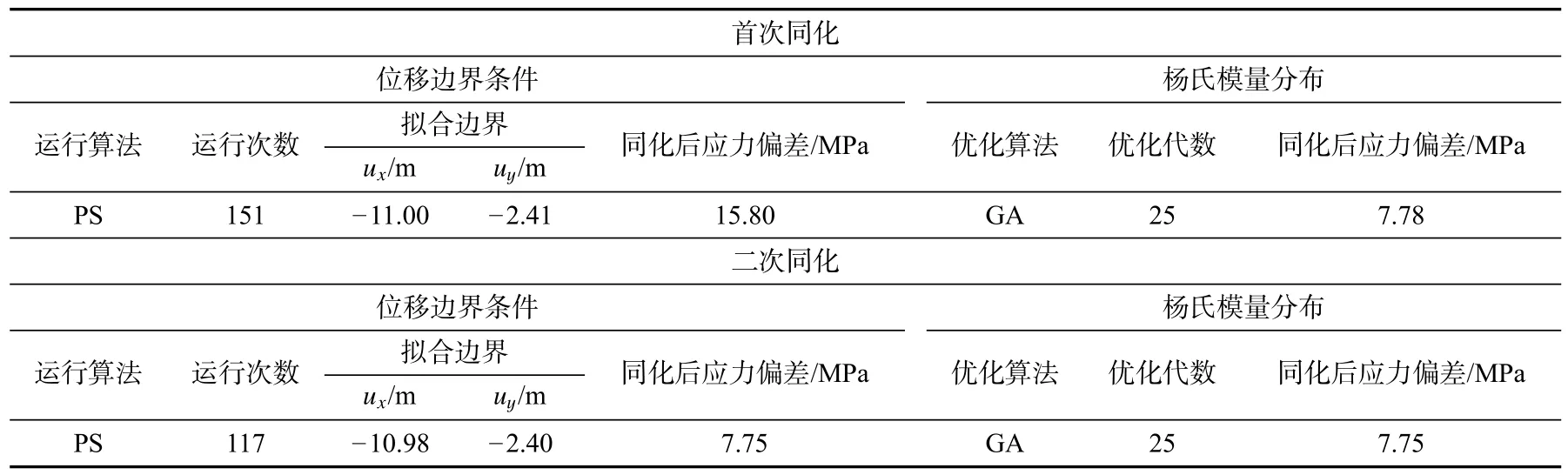
表7 实际算例计算结果Tab.7 Calculating results of practical case
初始场和同化场的应力比较如图14∼图16 所示。由于第二轮同化产生的目标值变化较小,这里只展示第一轮同化后的结果。图17 将数据同化过程中每个步骤后的计算应力与解释值进行比较,图中参考为一维地质力学分析的解释应力,初始为通过边界条件和杨氏模量分布初始猜测计算的应力,同化BC 为第一轮边界条件同化后获得的结果,同化E 为第一轮杨氏模量同化后的结果。从图17 可以看出,解释应力和初始猜测之间的差异相当显著。仅对边界条件进行同化不足以使模型结果与参考值匹配。杨氏模量场的同化有助于进一步提高地质力学模型与实际情况的一致性。

图14 杨氏模量场同化结果Fig.14 Assimilation results of Young′s modulus field
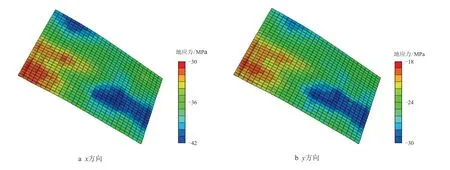
图15 初始地应力场分布Fig.15 The initial distribution of in-situ stresses
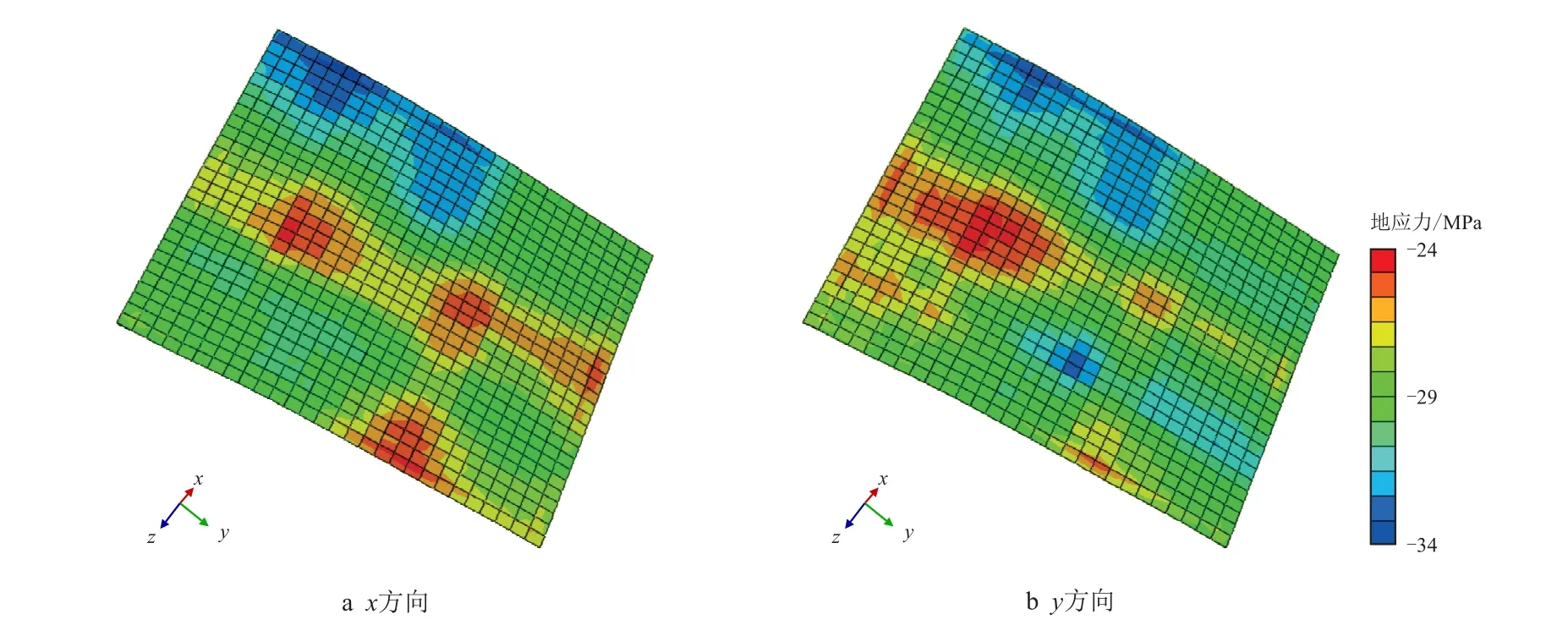
图16 一轮同化后地应力方向Fig.16 The distribution of in-situ stresses after 1st round of assimilation

图17 参考点沿x和y 方向的地应力比较Fig.17 Comparison of in-situ stresses alongxand y directions at observation locations
3 结论
(1)利用KL-E 生成地质力学参数场可以大大减少每次同化计算时需要更新的未知数。测试算例计算结果表明,采用本文提出的算法同化得到的地质力学属性参数场分布与实际情况较为接近。当应用于实际算例时,本文算法也可有效提高模型计算应力与参考应力的吻合度。
(2)相比属性参数场,边界条件的同化收敛速度更快。通常只需要两次序贯同化边界条件和地质力学属性参数场,目标值将停止显著变化。

