基于声波信号预测Kaiser 应力点的水平地应力

范翔宇，么勃卫 ，张千贵，夏宏泉

1.西南石油大学地球科学与技术学院，四川 成都 610500；2.油气藏地质及开发工程国家重点实验室·西南石油大学，四川 成都610500 3.西南石油大学石油与天然气工程学院，四川 成都610500

引言

地应力是开展深部地层工程设计不可或缺的重要基础数据，尤其是油气井工程领域，准确地预测地应力是安全施工设计的基本保障[1-3]。石油工程领域中，地应力的评价主要包括地质资料的定性分析、矿场实测数据分析、岩芯实验数据分析及测井资料计算4 种类型[4-7]。地质资料定性分析主要通过分析断层类型、取芯收获率、构造特点等资料确定地应力的大小与方向，其结果误差较大。矿场实测数据分析方法主要包括水力压裂测试分析和井壁崩落地应力反演分析，其中，水力压裂法测定得到的最小水平主应力值，在一定精度范围内可视为地应力的直接测量值。实验数据分析法主要包括古地磁-差应变、Kaiser 效应声发射测试、应力恢复法等[8]。虽然矿场实测数据分析方法和岩芯实验数据方法具有较高的精确性，但是获得的测量结果数据离散，且地应力评价成本较高。然而，基于岩石声学特征的测井评价方法计算地应力具有成本低、信息量大、测量深度大、数据连续等优点，已被石油工程领域广泛接受。

近年来，基于岩石声学特征测井评价方法的地应力计算模型因现场实践及理论的不断补充而得以发展。较为典型的如，Mattews、Eaton 等[9-10]在考虑骨架应力系数的基础上建立测井计算模型；Anderson 等[11]基于多孔介质材料弹性变形理论，完善了前人的测井计算模型，建立了Anderson 模型；后来针对低渗透且有微裂隙地层对Anderson 模型进行修正，建立了Newberry 模型[12]；针对构造应力较强地层出现了黄氏模型和葛式经验关系式等[13-15]。虽然，这些地应力评价模型针对不同地区和不同地层已得到了长足发展，但其地应力评价精度仍然受到实际地层压力较难预测、应力参数难以确定、地应力不连续特征等因素的影响，其预测精度显著低于矿场实测数据分析方法和岩芯实验数据方法评价结果。

因此，在实际工程应用中，往往需要矿场实测数据分析方法和岩芯实验数据方法评价结果对测井评价的地应力进行校正。然而，考虑到矿场实测数据分析方法和岩芯实验数据的地应力评价方法需要高昂的成本，若能构建一种综合岩石声学特征测井评价方法的经济性和评价结果的丰富性，及矿场实测数据分析方法和岩芯实验数据的地应力评价方法的准确性的地应力评价方法，将对石油工程领域，乃至众多深部工程领域具有重要的实际意义。

为此，本文根据岩石声学性质与力学特性具有较好的相关性特征，基于大量岩石试件的声波时差实验数据和加载条件下的声发射实验数据，进行构建声波时差与岩样Kaiser 应力点的相关性研究，并结合岩石声发射实验预测地应力计算模型，开展基于声波信号预测Kaiser 应力点的地应力计算方法研究，并对提出的地应力评价方法进行误差分析。

研究成果对于丰富和发展深部地层地应力评价技术和深部地层工程设计与施工具有重要的理论和实际意义。

1 声波时差与Kaiser 应力点的关系

按照声发射测试地应力要求取样，先将这些岩样进行模拟地层温压条件的声波测试，然后对这些岩样进行声发射实验，建立岩样声波与声发射Kaiser 应力点的关系。

1.1 声发射实验试样

实验样品所用全尺寸岩芯取自鄂尔多斯盆地陇东地区储油层直井段，以长石砂岩、岩屑长石砂岩和岩屑砂岩为主，岩性致密，具有低孔低渗的特点。根据声发射实验测量地应力取样方法，如图1 所示。

图1 全尺寸岩芯钻取声波时差与声发射实验试样示意图Fig.1 Schematic diagram of drilling small-size cores from a full-scale stratum rock sample for acoustic emission tests and acoustic emission tests

对直井段全尺寸岩芯试样进行了小尺寸试样钻取，水平方向按照45°夹角分别钻取3 件试样，取样方式根据SY/T6351—2012《岩样声波特性的实验室测量规范》和GB/T23561.9—2009《岩石三轴强度及变形参数测定方法》，试样的尺寸为ϕ25 mm×50 mm，共钻取了28 组岩芯样品，共计112件（部分试样见图2）。

图2 制备好的部分岩芯试样Fig.2 Part of the small-size cores

如图3 所示，采用SCMS-E 高温高压岩芯声学测量仪，该仪器进行岩石声速测试时的纵波发射频率为fp=1 MHz。

图3 SCMS-E 高温高压岩芯声学测量仪Fig.3 SCMS-E high temperature and high pressure core acoustic measurement instrument

仪器精度为：长度测量误差为±0.02 mm；直径误差为±0.02 mm；质量称重误差为±0.000 1 g；纵波时差测量范围为150∼1000 μs/m，纵波时差误差为±2%。测量时，探头与岩样之间加耦合材料，在其一端用发射探头向岩石发射脉冲信号，在另一端接收声信号。

对上述112 块标准岩样进行声波测试。对端面磨平的试样进行模拟地层温压条件（Tg=2°C/hm，pcg=1.46 MPa/hm）的动态声学参数测量。

将实验声波数据按照测井频率（fcp=20 kHz）进行频散校正，实验岩样纵波时差计算公式[16]为

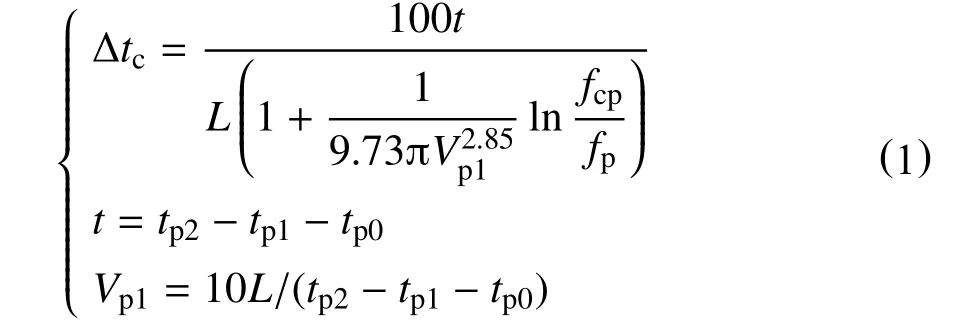
式中：

∆tc—岩样纵波时差，µs/m；

L—岩样的长度，cm；

t—纵波信号在岩芯中的传播时间，µs；

tp1—纵波信号到达探头1 的时间，µs；

tp2—纵波信号到达探头2 的时间，µs；

∆tp0—纵波在探头1、2 中传播的总时间，∆tp0=7.06µs；

Vp1—实验仪器在原始频率下测量的岩芯纵波速度，km/s；

fcp—纵波测井频率，kHz；

fp—实验仪器声波发射频率，kHz。

1.2 岩石声发射实验与Kaiser 应力点的确定

1.2.1 岩石声发射实验

试件的加载实验采用MTS 三轴岩芯电液伺服压缩实验系统（图4a），该实验系统主要由轴压系统、围压系统、孔压系统、加温系统和微机控制系统五部分组成。其技术指标如下：轴向最大实验力为2 200 kN，最大围压可达120 MPa，最大孔隙压力可达65 MPa，最高温度可达160°C。声发射信号采用美国物理声学公司研制的LocanAT-14ch 型声发射采集仪（图4b）进行测定，该设备广泛应用于岩石及岩体中的声发射监测。

图4 岩石声发射实验设备Fig.4 Acoustic emission test equipment for rock

为反映岩石在深部地层环境的声发射特征，实验采用模拟地层温度（2 °C/hm）与应力条件（1.46 MPa/hm）进行岩石声发射实验，实验温度取45∼75 °C，围压取15∼40 MPa，单个岩芯实验温度与围压根据钻取岩芯埋深与相关梯度进行估算得到，实际测试温度与围压如图5 所示。

图5 岩石声学实验与声发射实验测试温度与围压Fig.5 Test temperature and confining pressure of acoustic emission tests and acoustic emission tests

详细实验步骤如下：

（1）将已完成声波时差测试的岩石试件端部涂抹聚四氟乙烯薄膜以减少端部摩擦产生的噪声，实验前在试件端部放置橡胶垫片。

（2）将试件放置在压力室下承压杆上，试件上端放置上承压杆，并套上热缩管，采用电吹风向热缩管吹热风，使之与上下承压杆和试件紧密结合，采用金属环固定好热缩管的两端，而后在试样两端安装轴向引伸计支座与轴向引伸计，在试样中间位置安装链条式环向引伸计，并连接好引伸计信号线。

（3）安装压力室，并注入液压油，待注满后按照0.05 MPa/s 增加压力室三向压力至围压设定值，并增加温度至设定值，见图5。保持该三向应力与温度直至2 h 内试样不发生变形。

（4）将8 个声发射接收探头固定在压力室周围，并连接至LocanAT-14ch 型声发射采集仪。

（5）保持围压不变，以0.1 MPa/min 加载速率增加轴向应力，同时启动声发射采集仪，并采用计算机记录荷载、试件轴向与环向应变，以及声发射信号，当试件破坏，停止实验，卸除围压，取出试样。

按照上述步骤，根据实验方案进行下一岩样声发射实验。

1.2.2 岩石Kaiser 应力点的确定

根据声发射测试地应力的基本理论，岩芯加载到所受应力达到该岩样历史最大时，会伴随大量的声发射信号[16-24]。做声发射应力与取对数的累计能量和振铃计数的关系图，如图6 所示。可以看出，在累计能量曲线的拐弯处与振铃计数出现明显高值时，该时刻对应的应力值即为确定的声发射Kaiser 应力点。

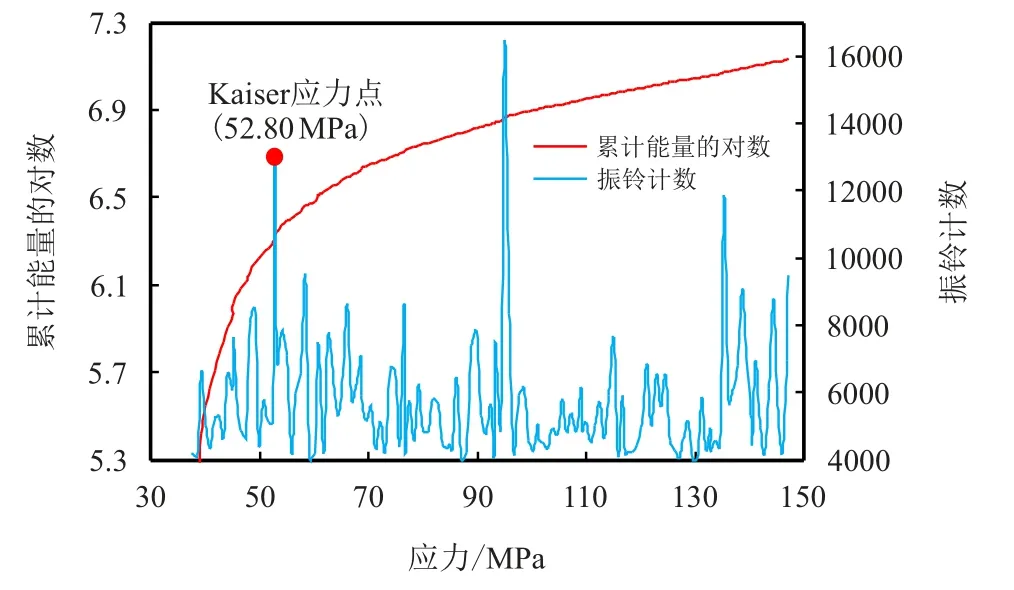
图6 岩石声发射累计能量的对数与振铃计数随应力变化的曲线Fig.6 Curves of the logarithm of AE cumulative energy and ringing counts vs.stress

1.3 岩石声波时差与Kaiser 应力点关系的构建

根据上述岩石声波时差测试和加载条件下的声发射实验结果，将相同岩芯试样的纵波时差值和Kaiser 应力值绘制到纵波时差Kaiser 应力图版，见图7。

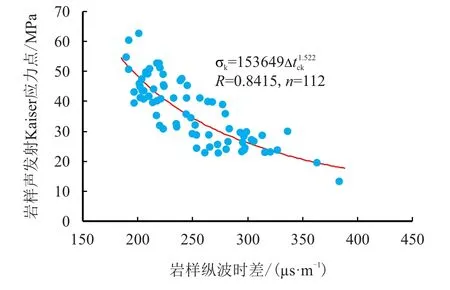
图7 岩样纵波时差与Kaiser 应力点关系图Fig.7 Relationship between interval transit time of longitudinal wave and Kaiser of rock

从图7 可以看出，测试岩石试样的纵波时差和Kaiser 应力具有较好的幂函数关系，如式（2）所示，其相关系数达到0.841 5。

式中：σk—Kaiser 应力值，MPa；

∆tck—测井声波时差，μs/m。

根据上述分析可知，岩石声波时差值与Kaiser应力值具有较好的幂函数关系，故二者相关关系可以采用式（3）表示

式中：

a—纵波时差与Kaiser 应力点构建关系乘法系数，无因次；

b—纵波时差与Kaiser 应力点构建关系指数，无因次。

2 基于声波时差预测Kaiser 应力点的地应力计算模型

2.1 岩石声发射实验预测地应力模型

采用如图1 所示，从地层垂直方向钻取的全尺寸岩芯上，沿增量为45°的方向钻取3 块小尺寸岩芯试样。

根据三轴实验条件下的岩石声发射实验原理，测出3 个方向的Kaiser 应力值，可利用式（4）求出水平最大、最小地应力

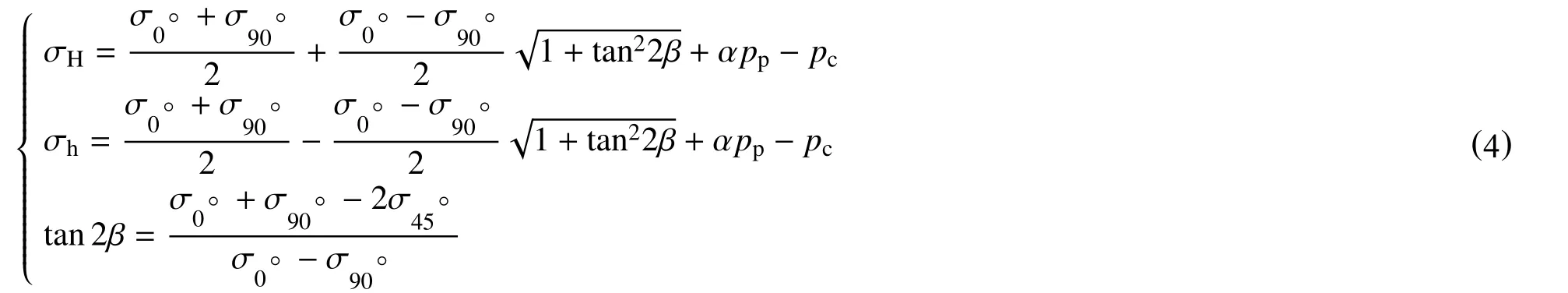
式中：σ0°—0°水平方向Kaiser应力值，MPa；

σ45°—45°水平方向Kaiser应力值，MPa；

σ90°—90°水平方向Kaiser应力值，MPa；

σH—最大水平主地应力，MPa；

σh—最小水平主地应力，MPa；

α—孔弹性系数，无因次；

pp—地层孔隙压力，MPa；

pc—高压井筒内岩芯承受的围压，MPa；

β—岩芯坐标与井筒坐标相差角，（°）。

2.2 孔隙压力的声波时差表征

根据不同深度但具有相同的岩石物理性质的骨架所受到的有效应力相等原理，Eaton 孔隙压力计算模型

式中：

po—上覆岩层压力，MPa；

pw—地层静液压力，MPa；

∆tn—将岩样深度代入正常压实趋势线上的纵波时差值，μs/m；

c—压实指数，无因次。

在2 000 m 以上地层平均密度取2.31 g/cm3，压实指数常取0.914。在实际工程应用中，利用密度测井曲线值积分计算上覆岩层压力po，提取泥岩层声波数据，建立正常压实趋势线，根据岩样所在地层垂深，读取等效声波时差。

式中：He—等效垂深，m；

M—正常压实趋势线乘法系数，无因次；

N—正常压实趋势线加法系数，无因次。

2.3 预测Kaiser 应力点的地应力计算模型

声发射实验预测地应力计算模型是将模拟地层温度和应力实验条件下测试获得的3 个水平岩芯的Kaiser 应力点（σ0°、σ45°、σ90°）的值代入式（4）进行计算，从而求得最大水平地应力和最小水平地应力。

而根据图7 所示，岩石Kaiser 应力点与声波时差具有较好的指数相关关系[式（3）]，由此，将式（3）代入式（4），并考虑pp的声波时差表征[式（5）]，得到基于声波信号预测Kaiser 应力点的水平地应力计算模型

式中：∆tc1—c1 点纵波时差，μs/m；

∆tc2—c2 点纵波时差，μs/m；

∆tc3—c3 点纵波时差，μs/m。

3 实例应用分析

实例应用分析研究工区为鄂尔多斯盆地陇东地区储油层直井C6、C7、C8 段。

3.1 模型参数确定

通过岩石三轴实验测试得到该地区致密砂泥岩的孔弹性系数（α）为0.5，取研究工区泥岩层纵波时差∆tn，建立工区不同泥岩层深度与纵波时差测井值的正常压实趋势线，如图8 所示。

图8 工区地层纵波时差的正常压实变化趋势线Fig.8 Normal compaction trend line of the interval transit time of longitudinal wave of the study formation

密度测井曲线直观地反映不同深度地层段的岩石密度，用密度测井曲线计算上覆岩层压力

式中：H1—未测井段的地层垂深，m；

ρ1—未测井段的地层密度，g/cm3；

ρi—不同深度井段密度测井值，g/cm3；

Hi—密度测井第i段井深采样间隔，m。

采用从地层垂向钻取的全尺寸岩样在模拟地层温度和压力条件下进行360°声波扫描获得声波速度。测试获得断面纵波波速如图9 所示。按照上述方法，对整个储层段（井深1 630∼1 790 m）全尺寸岩样间隔2.54 cm，以此得到研究地层直井储层段全尺寸岩样的360°纵波波速数据。而后选择连续的测量数据按照任意方位为0°，间隔45°和90°提取纵波波速，并计算其倒数获得3 个方位的纵波时差值（∆tc1,∆tc2,∆tc3）。

图9 360° 声波扫描全尺寸岩样获得的纵波波速数据Fig.9 P-wave velocity obtained by 360° sonic scan for the full-scale stratum rock sample

模型中，砂岩层骨架纵波时差取174 μs/m，泥岩层骨架纵波时差取345 μs/m，地层流体纵波时差取620 μs/m，静液压力按照井深梯度0.7 MPa/hm 计算，围压根据不同井深按照pc=po−pw计算。

3.2 模型预测效果分析

将获得的相关参数和岩芯声波时差数据，利用建立的基于声波信号预测Kaiser 应力点的水平地应力计算方法，分析获得研究工区储层段最小水平地应力和最大水平地应力。同时，利用该井段测井数据，根据Anderson、Eaton 和Newberry 模型计算获得最小水平主应力和最大水平主应力。利用上述4种计算方法得到的研究井段水平地应力值如图10所示。此外，该井段进行了5 次水力压裂实验，利用水力压裂实验计算地应力的方法，得到了5 个点的最小水平地应力值，见图10 中实测数据。从图10可以直观地看出，利用声波预测Kaiser 应力点地应力模型与水力压裂实验数据计算的地应力（图中蓝色标记段为水力压裂施工段最小水平主应力实测值）吻合程度好。不同井深孔隙压力pp和上覆岩层压力po及其他力学和测井参数见图10。

图10 研究储层段不同地应力模型计算与水力压裂实测结果（1 630∼1 790 m）Fig.10 Horizontal in situ stresses of the study reservoir section obtained by different evaluation method and hydraulic fracturing test（1 630∼1 790 m）

Anderson、Eaton 和Newberry 模型和本文提出计算方法分析得到的最小水平地应力与水力压裂实验数据计算值的误差分析见表1。从表1 中可以看出，Newberry 模型计算结果与水力压裂实验数据计算的水平最小主应力偏差区间为31.31%∼40.22%，平均误差34.68%。Anderson 模型计算的水平最小主应力与水力压裂实验数据计算的最小主应力偏差区间为4.11%∼26.96%，平均误差21.62%。这两个模型计算结果误差都超过了工程施工精度。Eaton模型和声波信号预测Kaiser 应力点地应力模型平均误差分别为7.73%和7.97%，以此结果分析，Eaton模型精度更高一些，满足工程施工精度，但是该模型误差范围为3.81%∼12.33%，误差跨度8.50%。反观声波信号预测Kaiser 应力点地应力模型误差范围为5.52%∼10.05%，误差跨度4.53%。计算结果相对比较稳定，该模型预测结果与现场水力压裂实验实测结果吻合度好，不失为一种较实用的地应力计算方法。

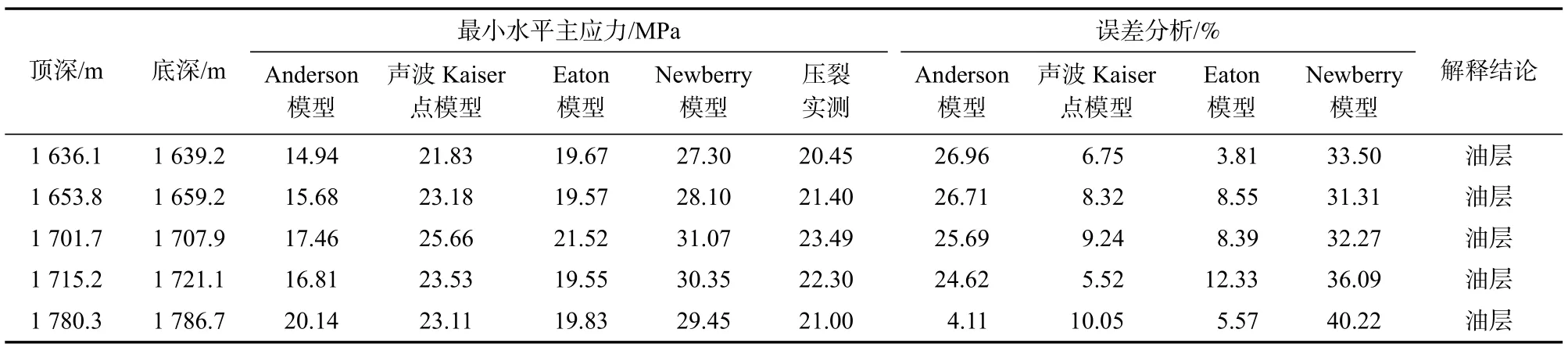
表1 多个实验工区预测与实测地应力数据对比Tab.1 Comparison between predicted and measured in-situ stress data of several test areas

综上，基于单轴应变的多孔介质弹性Anderson模型和Newberry 模型对于致密砂岩低渗透储层地应力计算不太适用，Eaton 模型纵向计算结果不够稳定，需要校正才能在工程中使用，基于纵波信号预测Kaiser 点的地应力计算模型具有纵向连续性好、误差小、计算结果稳定等特点，说明本文提出的地应力评价方法具有较好的工程实用性。

4 结论

（1）声波信号可以反映岩石的力学性质，测试岩石试件的纵波时差和Kaiser 应力值具有较好的幂函数关系。

（2）用测井资料和全尺寸岩芯试件的360°扫描声学参数，构建的声波时差与岩样Kaiser 应力点的关系函数，基于岩石声发射实验预测地应力计算模型，建立了利用声波信号预测Kaiser 应力点的地应力计算模型。

（3）将Kaiser 点预测地应力模型、Eaton、Anderson、Newberry 模型与水力压裂实验数据得到的最小水平地应力值进行对比分析，提出的地应力评价新模型合理，精度更高。

（4）基于纵波信号预测Kaiser 点的陇东地区地应力计算方法结果合理稳定，相对于矿场实测方法和岩芯实验的地应力评价方法，该方法可获得更为丰富和连续的地应力评价数据，具有更好的经济性。