柯西不等式应用的技巧策略

孟璐璐

(山东省邹城市实验中学)

柯西不等式是不等式选讲部分的主要内容,也是历年高考数学试卷中的重要考点,常考常新,形式多样.高考数学试题中,经常借助柯西不等式来求解相关代数式的最值问题.而在实际利用柯西不等式时,要合理根据柯西不等式自身的结构,对题目条件或结论中的相关代数式进行适当的转化与变形,进而利用柯西不等式来分析与求解.具体求解过程中要熟练掌握柯西不等式的应用技巧策略,如凑项、拆项、分解、组合等.

1 凑项

凑项的技巧是根据题目条件或结论中代数式的结构特征,合理对关系式进行必要的配凑处理,在涉及一些根式、分式等相关问题中,经常利用常数的凑项、含参代数式的配凑等技巧处理,进而利用柯西不等式巧妙求解.

例1若x＞0,y＞0,且＝1,则2x＋y的最小值为( ).

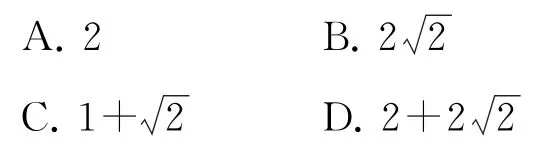
分析结合题目条件中的二元方程,通过对所求的二元代数式进行合理配凑,对比条件中代数式的结构特征,结合系数与线性转化,利用乘“1”处理,进而借助柯西不等式确定对应代数式的最值问题.

分析题目条件与所求结论之间代数式的结构特征与联系,进行合理的凑项,为利用柯西不等式确定代数式的最值提供保障.凑项的技巧就是使得利用柯西不等式后所得的关系式为常数,达到消元的目的,进而巧妙求解最值.

2 拆项

拆项的技巧是根据题目条件或结论中代数式的结构特征,合理对关系式进行必要的拆分处理,包括对常数的拆分、代数式中系数的拆分等多种方式,构建满足柯西不等式的条件,再利用柯西不等式分析与求解.

例2已知正实数a,b满足a＋b＝1,则的最小值为________.

分析根据题目条件对常数进行拆项处理,即利用条件中的代数式进行合理拆分,联系题目条件与结论中代数式的特征,应用均值不等式、柯西不等式确定对应代数式的最值.

利用均值不等式或柯西不等式解决代数式的最值问题时,需要注意相关条件、结论中代数式的系数,必要时要进行拆项处理,通过合理拆分,确定对应不等式等号成立的条件,这是问题获解的关键.

3 分解

分解的技巧是指根据题目条件中关系式(或结论中代数式)的结构特征,合理对关系式进行必要的分解处理,特别是在一些多元(三元及以上)代数式以及相关问题中,要巧妙分解,进而利用柯西不等式分析与求解.

例3已知x,y,z为正实数,且x2＋y2＋z2＝3,则＋yz的最大值是_________.

分析根据题目条件对三元平方和的关系式进行合理的消元转化和分解,进而通过柯西不等式对代数关系式进行恒等变形,最后再利用基本不等式确定相应的最值问题.

解由题设条件x2＋y2＋z2＝3,可得x2＋z2＝3-y2.由柯西不等式可得

解题时需要根据相应代数式的结构特征进行必要的分解处理,特别是一些常数的分解或代数式乘积的分解等.本题根据所求代数关系式的特点将三元平方和的关系式进行消元与分解处理,进而利用重要不等式来巧妙转化,这是破解问题的关键所在.

4 组合

组合的技巧是根据题目条件或结论中代数式的结构特征,合理对关系式进行必要的组合,特别是对分式中分子与分母之间的对应关系进行处理,最终利用柯西不等式确定最值.

例4已知a＞0,b＞0,满足＋2b＝4,则的最小值为_________.

分析对题目条件中的双变元方程与所求代数式进行比较,联系条件与结论之间的关系,对相关的代数式进行合理恒等变形,最终利用柯西不等式确定代数式的最值.

熟练掌握柯西不等式以及对应的公式,合理对相关的代数式或常数进行必要的分解,为进一步利用柯西不等式确定代数式的最值提供保障.对相关的代数式或常数进行分解的依据就是合理消元,巧妙确定最值.

柯西不等式是学生应掌握的基本知识点,是一个比较常用的不等式.实际利用柯西不等式求解相关代数式的最值问题时,若不能直接利用柯西不等式,则要对相关不等式进行巧妙处理,合理应用凑项、拆项、分解、组合等技巧策略.而有些代数式最值问题的解决需要反复利用柯西不等式才能达到目的,需要注意的是在运用的过程中确保每一次运用柯西不等式时,前后等号成立的条件必须一致,不能自相矛盾,否则就会出现错误.

(完)