电动客车动力总成悬置参数优化设计
薛宏斌, 朱晓禹, 邱钰贤, 翁 涛, 朱红军
(中车时代电动汽车股份有限公司, 湖南 株洲 412007)
燃油客车悬置系统优化设计的着眼点多是发动机的扭矩波动,而电动客车采用电机驱动,其振动激励形式与内燃机有很大的差异,电机的扭矩波动远低于发动机,但电机的扭矩明显大于同级别的发动机,所以电动客车对其动力总成悬置系统的抗扭限位能力要求远大于燃油客车,即其动力总成的悬置刚度要远大于燃油客车的悬置刚度。但过大的刚度会引起悬置隔振效果的下降。本文对某电动客车动力总成悬置参数进行优化,在抗扭和隔振作用中寻求最佳刚度平衡点。
1 动力总成悬置系统的振动模型
本文电动客车动力总成包括电机、减速器、电机控制器等。为满足整车舒适性需求,动力总成悬置系统应合理设计系统的刚体模态频率,并尽可能使其振动模态相互解耦。模态频率的不合理分布易引发共振;解耦率太低会放大动力总成各方向的振动,进而降低悬置隔振效果。
1.1 动力总成悬置系统的振动模型
电动客车动力总成悬置系统的刚体模态频率一般不大于60 Hz,相比弹性体模态频率要低很多。所以在进行振动分析时可以将动力总成当作刚体来处理。此时可将动力总成悬置系统简化为6自由度的振动模型进行分析,如图1所示。动力总成由个悬置支撑,点是其质心位置,、、表示第个悬置三个互相垂直的主刚度轴,、、表示各向对应刚度,、、表示第个悬置的各主刚度轴与动力总成坐标系各坐标轴之间的夹角。

图1 动力总成悬置系统的6自由度模型
1.2 动力总成悬置系统的仿真模型
利用ADAMS软件搭建动力总成悬置系统的仿真模型进行仿真分析。在建模时采用弹性连接约束(Bushings)来模拟悬置元件,图3为图2在ADAMS软件中建立的仿真模型。

图2 动力总成悬置系统三维模型

图3 动力总成悬置系统ADAMS仿真模型
2 动力总成悬置系统解耦分析
某电动客车加速工况下车内振动噪声大,可能是其动力总成悬置隔振能力不足所致。从隔振理论可知,这与其刚体模态频率的分布和系统的解耦率密切相关。本文1.2节建立了简化后的动力总成悬置系统仿真模型,本节在此基础上进行固有模态频率和解耦率分析。
2.1 原动力总成悬置系统固有频率和解耦率
在进行动力总成悬置系统固有频率和解耦分析时,通常将振动系统简化为无阻尼的自由振动系统,即:
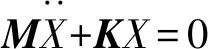
(1)
求解式(1)的特征值和特征向量可得到系统的刚体模态频率和模态振型。当系统以第阶固有频率振动时,系统的总动能计算公式为

(2)
式中:表示质量矩阵中的第行第列元素;()、()分别表示振型的第个、个元素。
分配到第个自由度上的动能值为

(3)
第阶模态分配到第个自由度上的动能占系统总动能的比例(即系统解耦率)为
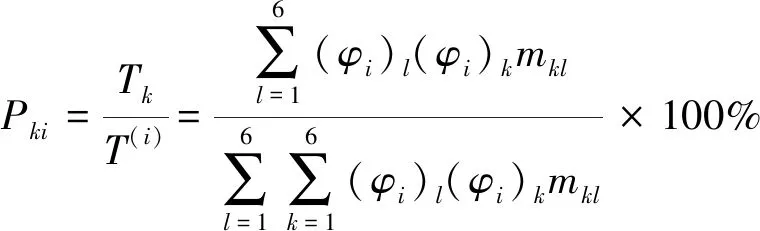
(4)
如果=100%,则系统第阶模态的各自由度间不存在耦合,即系统解耦率为100%。
2.2 动力总成悬置系统的ADAMS解耦结果
本文动力总成质量为117 kg,前后左右悬置的、和向静刚度分别为800 N/mm、180 N/mm和800 N/mm,动静刚度比为1.4,其他参数见表1和2。

表1 动力总成质心、悬置坐标 mm
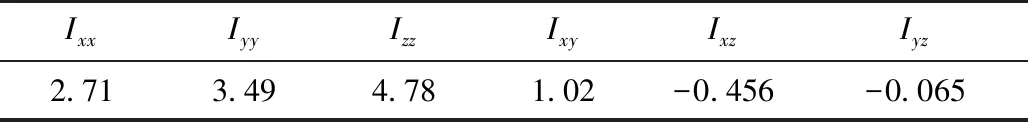
表2 动力总成惯量 kg·m2
基于上述参数值,通过ADAMS/Vibration频域计算模块对1.2节所建立的仿真模型和2.1节中的式(4)进行分析,求得动力总成悬置系统的刚体模态频率和各自由度动能比见表3。
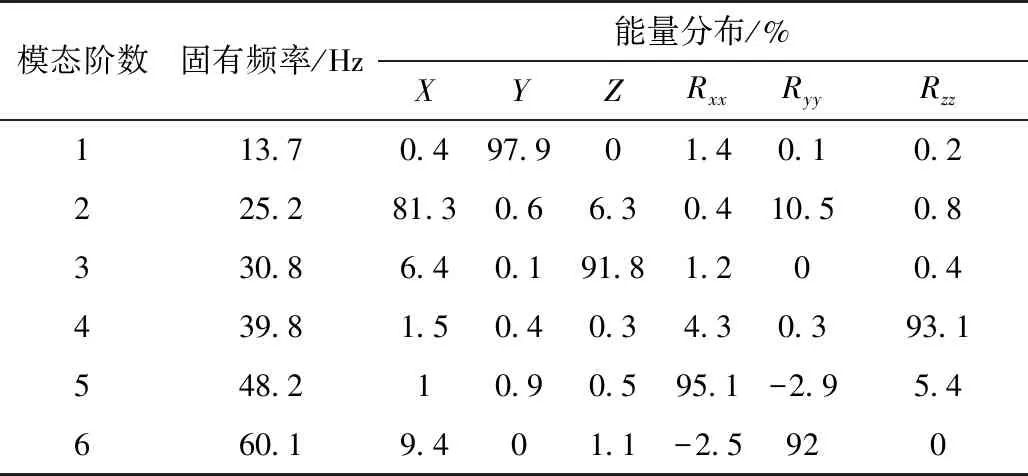
表3 动力总成悬置系统能量分布百分比

3 动力总成悬置系统优化设计及结果
3.1 优化原理
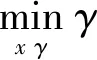
()-·≤
(5)
满足约束条件
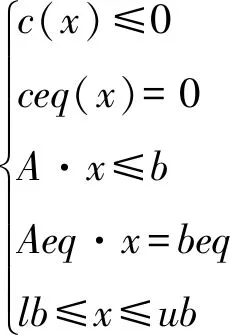
(6)
其最常用的调用格式为=fgoalattain(,0,,,,,,,,,),其中是目标函数,0是初始值,是目标值,是目标值权重,、定义不等式约束·≤,、定义等式约束·=,、定义上下限约束≤≤,是用M文件定义的非线性约束。
3.2 定义的约束条件

2) 悬置刚度约束。悬置刚度大虽然可以增加悬置系统的抗扭能力,降低动力总成与邻近部件的干涉情况,但是太大的刚度会降低其隔振效果,从而引起悬置系统振动传递率的上升;而悬置刚度过小又不利于悬置对动力总成的支撑。考虑到悬置材料的特性及其他同级别车型数据,本文将悬置元件的刚度参数约束在100~550 N/mm之间。
3) 空间位置约束。如果考虑通过改变悬置的空间位置来提升动力总成悬置系统的解耦效果,那么必须要校核悬置安装的空间条件,但在实际工程中常常受到动力总成安装位置的限制。在本次优化工作中,动力总成和悬置相对于整车的空间位置已经确定,所以对悬置空间位置不再进行约束。
3.3 优化结果
优化结果见表4和表5。可以看出,优化设计后动力总成悬置系统以某阶固有频率进行振动时,其主振动方向的能量与总能量的比值均大于90%,解耦效果较好;各自由度模态频率在10~46.4 Hz之间且模态频率分布间隔均大于3 Hz,可以有效避免因动力总成刚体模态耦合造成的悬置隔振性能下降;刚体模态最大频率值(自由度)由60.1 Hz降低到43.1 Hz,能有效提升常用工况下动力总成悬置系统的隔振性能。

表4 悬置刚度优化结果 N/mm
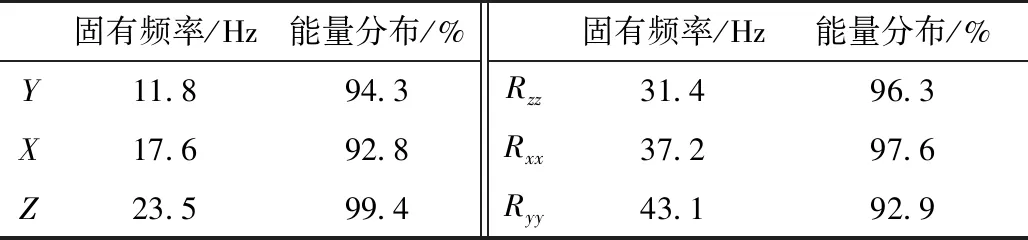
表5 悬置优化后的固有频率和能量分布
3.4 实车验证
悬置系统的隔振效果可以通过计算悬置主动端和被动端加速度的比值(即悬置隔振率)来评估,隔振率越大,则悬置的隔振性能越好。悬置隔振率的计算常用 dB形式,其公式为
=20·lg(||||)
(6)
式中:、分别表示悬置主动端和被动端的加速度值。
常用工况下电动客车要求悬置能隔绝90%以上的振动(即隔振率≥20 dB)。本文悬置优化前后的隔振率如图4所示。由于加速传感器只有3个移动自由度的数据,所以只能分析、、三个自由度方向的隔振率。从图中可以看出,优化前向和向的隔振率均小于20 dB,隔振效果不太理想;优化后、、三个方向的隔振率均有不同程度的改善且都大于20 dB。此外,优化后常用工况下(电机转速3 936 r/min)、、自由度方向的隔振率均超过了20 dB(一些转速下甚至达到29 dB),悬置系统的隔振能力大大提升。其主要原因是通过悬置系统的刚度优化使悬置系统的固有模态频率的分布更加合理,有效地避免了与动力总成刚体模态耦合造成的悬置隔振性能下降。
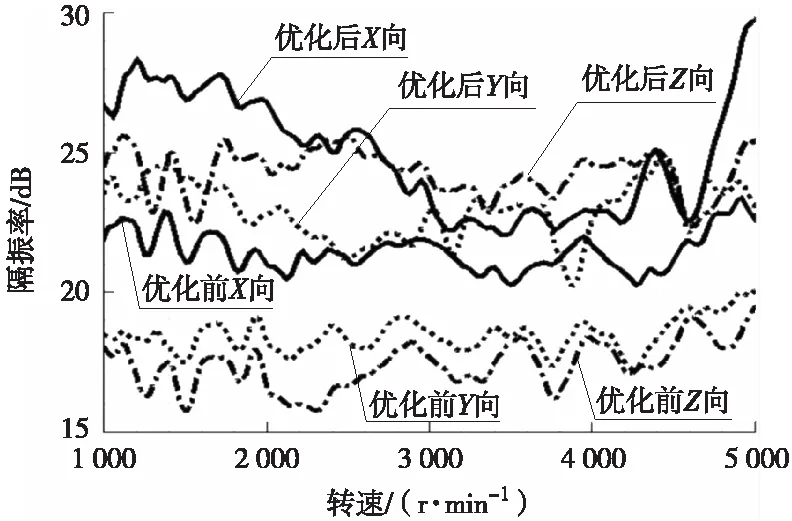
图4 左后悬置优化前后隔振率曲线
4 结束语
本文对电动客车动力总成悬置系统解耦理论进行阐述,并建立了该系统的动力学模型,通过分析得出悬置系统存在不同程度的耦合,然后运用MATLAB多目标优化工具进行悬置系统的优化设计,结果表明,通过优化悬置系统的解耦率和悬置系统的刚体模态频率分布可以有效增加悬置软垫的隔振能力,降低汽车行驶过程中产生的振动,为动力总成悬置系统的设计提供了宝贵的经验。

