分布式电驱动车辆电子差速控制算法研究
黄 玲
(厦门金龙联合汽车工业有限公司, 福建 厦门 361023)
相比于集中式驱动系统的机械差速功能,电子差速功能具有传动效率高、控制灵活等特点。电子差速控制主要用于分布式驱动系统,其算法对于差速功能有重要影响。本文提出一种分布式电驱动车辆电子差速控制算法,该算法以滑转率为控制目标,当驱动轮滑转率小于设定阈值时,基于垂向载荷进行左右电机的转矩分配;当驱动轮滑转率大于设定阈值时,基于滑模控制以设定阈值为目标进行电子差速控制,从而提升车辆在特殊工况下的操控稳定性。
1 电子差速控制算法
1.1 电子差速控制算法架构
首先,根据当前车速和加速踏板开度获得总转矩需求,再根据方向盘转角进行运动状态分析,结合车辆状态进行驱动转矩预分配,然后结合驱动轮滑转率大小,判断是否切换进入驱动防滑控制。若不满足切换条件,直接将转矩预分配结果输出到电机端;若满足切换条件,则驱动防滑控制进入滑模控制模式。电子差速控制算法架构如图1所示。
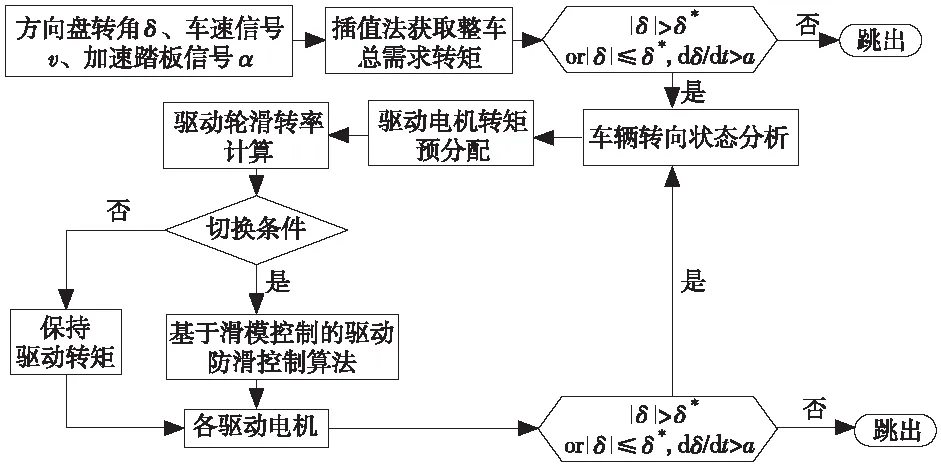
图1 电子差速控制算法架构
1.2 整车总需求转矩
在获取整车总需求转矩时,首先按照驾驶员输入的加速踏板开度和当前车速定义几个特殊工况(车辆蠕行、大加速和最高车速等),通过MATLAB/Simulink软件离线仿真确定这几个特殊工况的需求转矩值,其余工况需求的转矩值根据驾驶员的实际感受或经验进行调整,从而得到驱动转矩需求数据表格。根据表格数据通过MATLAB/Simulink软件绘制整车总需求转矩与加速踏板开度和车速的关系曲面,如图2所示。
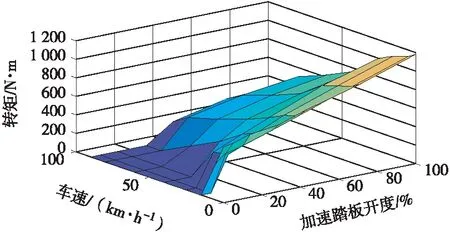
图2 整车驱动总转矩曲面
然后在MATLAB/Simulink软件的查表模块中,设置线性查表方式,可求得任意加速踏板开度和车速两个输入值对应的整车总需求转矩。
1.3 车辆转向状态分析
本文在理想阿克曼转向模型的基础上,考虑地面因素、载荷转移以及轮胎侧偏的影响,得到修正后的车辆转向模型,如图3所示。图中和分别为前轴内、外转向轮的侧偏角,为后轮侧偏角。

图3 修正后车辆转向模型
若设′=为转弯半径,则质心处速度=,其中为横摆角速度。由于(质心车速与车辆纵轴的夹角)很小,cos≈1,′≈,故有式(1)关系:
=arctan()≈≈
(1)
假设车辆左转弯,则前轴内外车轮的转向角和前、后轮侧偏角如式(2):
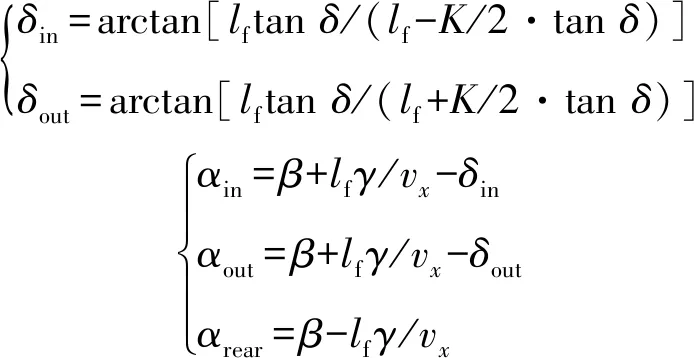
(2)
利用修正后的转向模型,以车辆质心速度为参考,计算两驱动轮绕转向中心的线速度,如式(3):

(3)
当车辆转弯时,受离心力的影响,会使轮荷发生转移,影响驱动轮的滑转率。其离心力的计算为
=(+)
(4)
客车一般为后轮驱动,后驱轮胎的垂直载荷分别为
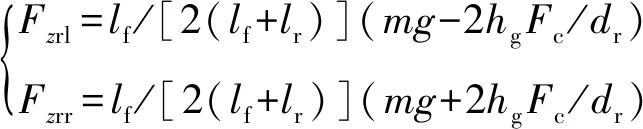
(5)
式中:为车辆质心高度。
1.4 驱动电机转矩预分配
车辆入弯时,左右驱动轮垂向载荷会发生转移,而地面纵向驱动力与垂向载荷成正相关。本文依据式(5)对左右轮的驱动转矩进行预分配,如式(6):
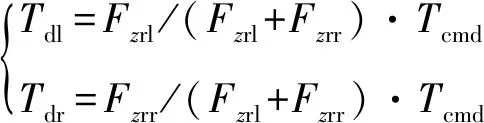
(6)
式中:、分别为左、右驱动轮转矩;为整车总需求转矩,通过1.2节获得;rl(rl+rr)和rr(rl+rr)分别为左、右驱动轮转矩分配系数,通过式(5)获得。
1.5 驱动轮滑转率计算
设置滑转率阈值,当实际滑转率>时,判断驱动轮发生滑转,进入驱动防滑控制,驱动转矩控制算法按1.6节进行;当实际滑转率≤时,判断驱动轮正常,此时按照式(6)预分配扭矩值进行左右驱动轮扭矩分配。
根据驾驶员的转矩需求和前轮转角输入,再结合路面状况及驱动轮偏转角变化率,采用比例控制来估算左右驱动轮在转向过程中的目标滑转率,再基于滑模控制对驱动轮独立分配转矩。
当轮胎在线性区域内进行中性转向时(即稳定性因素=0),其偏转角的变化率Δ估算如下:
Δ=(+)
(7)
由偏转运动决定的左、右驱动轮滑转率差值Δ,采用比例控制可以得到快速的控制响应。
Δ=(-Δ)=[-(+)]
(8)
式中:为比例系数。

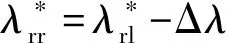
(9)
1.6 驱动防滑扭矩控制算法
本文采用滑模控制算法进行目标滑转率跟随时,选取滑模控制系统中误差为0的平面为控制跟踪的目标平面,选取切换函数为
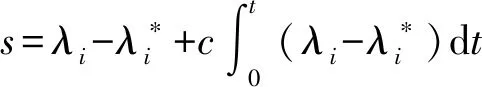
(10)
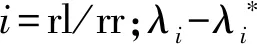
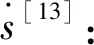

(11)
式中:代表趋近速度;为指数趋近率的斜率系数;为切换函数。>0时,符号函数sgn()=1;=0时,sgn()=0;<0,sgn()=-1。
对切换函数公式(10)求时间导数得:
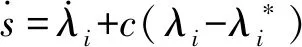
(12)
联合式(11)和式(12),有
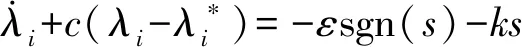
(13)
当车辆处于驱动工况时,车轮的滑转率定义为
=(-)
(14)
对上式求导得:
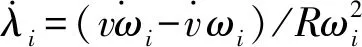
(15)
则上述受控系统可表示为
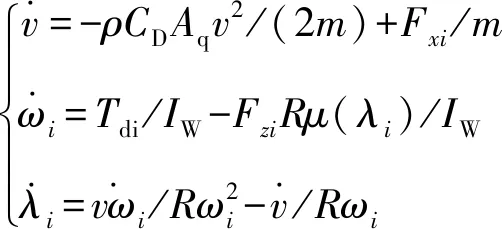
(16)
其中式1是纵向动力学平衡方程,式2是轮胎动力学方程。
联立式(13)、(16)可得滑转率控制器的控制转矩输入:
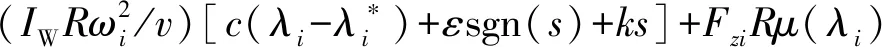
(17)
式中:为轮胎转动惯量;为空气阻力系数;为车辆迎风面积;为空气密度;为轮胎所受垂向力;()为路面附着系数。
2 仿真结果及分析
为了验证本文控制策略在车辆处于低附路面下的操稳性控制效果,以某12 m分布式电驱动城市客车为研究对象,在低附冰雪路面(最优滑转率=006,峰值路面附着系数=019)上,采用MATLAB/Simulink进行蛇形绕桩工况动力学建模和仿真分析。
整车相关参数:整车质量=13 500 kg,轮胎滚动半径=0.465 m,轮胎转动惯量=9.9 kg·m,整车绕轴的转动惯量=157 739 kg·m,车辆质心位置到前、后轴的距离=4.216 m、=1.884 m,车辆质心高度=0.964 m,前、后轮距=2.057 m、=1.91 m,轮胎侧偏刚度值==105 000 N/rad。
设定仿真时长为20 s,车速为36 km/h,加速踏板开度为100%,初始时刻前轮转角为0,最大转角为10°(0.174 rad)。仿真结果如图4所示。
从图4可以看出,当车辆刚驶入低附冰雪路面时,前轮转角开始以正弦波的形式变化,由于车辆以100%加速踏板开度驱动,在0 s时刻,左右驱动轮驱动扭矩均达到最大值(650 N·m),滑转率迅速接近1,出现严重的打滑现象,随后激活驱动防滑功能。在经过短时间(小于0.1 s)的震荡调节后,左右轮驱动扭矩迅速收敛,实际滑转率也趋于稳定,且跟随目标滑转率。由于本文驱动防滑控制兼顾了车辆的稳定性,所以在进行驱动防滑控制的过程中,车辆的质心侧偏角和横摆角速度能够控制在较小的范围内变化,且实际横摆角速度能较好地反映驾员的转向意图(横摆角速度变化趋势同前轮转角变化趋势一致),从而保证了车辆的操控稳定性,同时实现电子差速控制。

(a) 车辆实时状态相关参数曲线
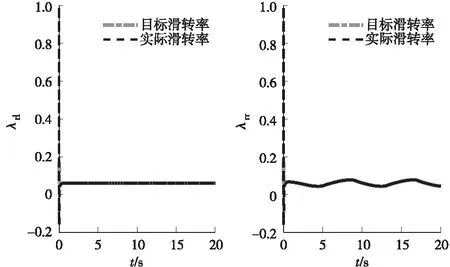
(b) 目标滑转率跟随
3 结 论
本文研究了分布式驱动系统的电子差速控制算法,基于转向稳定性以驱动轮滑转率为控制目标,同时考虑了车辆在转向过程中离心力的影响,通过滑模控制进行目标跟随。仿真结果表明,在低附冰雪路面上,采用本文控制策略能够将实际滑转率控制在目标值附近,从而实现稳定转向,同时也避免了轮胎的过度磨损。

