公交车辆智能调度系统开发及应用

孙玮佳， 林炳辉， 苏 亮， 任永欢

(厦门金龙联合汽车工业有限公司， 福建 厦门 361023)

由于乘客出行行为具有很大的随机性，所以传统公交按固定线路行驶停靠的模式，常常会造成公交空载率高、乘客等待时间过长等公交运力与乘客需求不匹配的情况。因此，基于互联网信息实时交互和GPS定位的智能公交调度系统便应运而生。该系统可实现乘客通过手机APP预约出行站点和时间，调度系统获取车辆实时位置，应用遗传算法规划最优公交行驶路线。该调度系统可最大程度提高乘客满意度，并使公交公司收益最大化，从而取得双赢。

本文从公交公司经济收益和乘客总时间收益两方面建立目标函数，应用遗传算法进行求解，决策车辆的最优行驶路径。最后通过与传统固定路线运营模式进行对比分析，得出该智能公交调度系统能有效提高公交公司的收益，减少乘客的等待时间。

1 智能公交调度系统介绍

1.1 智能公交调度系统概述

智能公交调度系统基于互联网实时接收乘客预约信息，GPS定位车辆实时位置，通过决策模块计算，决定是否响应乘客预约，并将决策结果反馈至乘客与驾驶员端。系统将运行线路上客流量大的站点定义为必停的固定站点，固定站点之间定义若干柔性站点，公交车会依据是否有乘客预约需求而决策是否停靠。该系统按固定时间间隔发车，当乘客发出预约请求时，决策模块通过计算公交公司运营成本和乘客时间两个目标函数，在满足一定约束条件的情况下，当综合效益最优时安排当前班次公交车响应预约，若综合效益不佳则默认安排后一班次响应。调度系统需将决策结果反馈给乘客和驾驶员，乘客确认后，按规定时间在预约站点上车，驾驶员按系统决策路线行驶。

1.2 智能公交调度系统架构

智能公交调度系统架构如图1所示。公交调度系统后台接收到乘客预约信息后，结合当前班次公交GPS定位，通过遗传算法计算并决策是否响应该预约。若决策响应，则将车辆预计到达时间反馈给乘客，乘客确认，提醒乘客及时到达乘车点，并反馈至驾驶员端，更新运行路线；若决策不响应，则将当前班次无法响应的信息反馈给乘客，并发送下一班次到达时间，驾驶员端无需反馈，按原路线行驶。

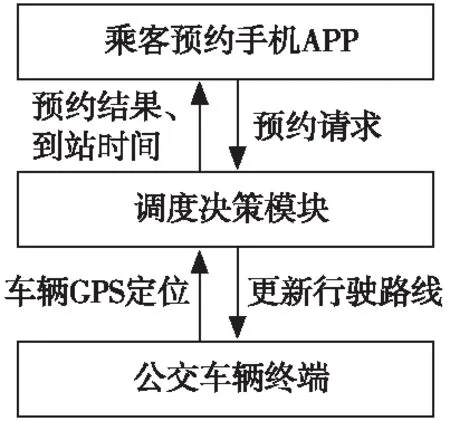
图1 智能公交调度系统架构

1.3 智能公交调度系统工作流程

调度系统主要分以下5个步骤：

1) 基础资料获取。包括公交票价、每公里运营成本、平均车速、乘客平均步行速度、站点坐标等信息，由公交公司针对具体运营线路统计得到，并输入到系统中。

2) 接收乘客预约信息。包括乘客预约上下车的站点、期望出发时间、出行人数等信息。

3) 决策调度。将步骤1)、2)所获得的信息输入到决策模块中，用遗传算法求解公交模型的收益和时间两个目标函数，得到使公交公司和乘客的综合收益最大化的公交运行路线。

4) 信息发布。决策结果发送至乘客手机端，乘客确认后，需按规定时间在预定站点上车，同时将更新后的路线发送至车辆终端，驾驶员按照指示行驶。

5) 持续接收乘客预约信息循环步骤2)～4)，直到车辆到达倒数第二个站点，结束调度，车辆直接驶向终点站。

2 智能公交调度系统算法模型

智能公交调度系统中的决策模块主要通过计算公交公司收益、所有乘客总时间收益这两个目标函数及时间窗约束来决定是否响应预约。

2.1 目标函数F1

目标函数主要由响应乘客预约而增加的票价收入(元)和为响应预约而导致增加的额外运营成本(元)组成：

=-

(1)

2.1.1 票价收入

票价收入为乘客人数与票价的乘积，如式(2)。由于该系统在乘客上车后可能因响应其他乘客需求，而导致车上乘客额外耗费时间乘坐多余路程。因此，为了提高乘客乘坐满意度和乘坐意愿，系统设计为乘客上车时只刷卡不扣费，到达目的地下车前再次刷卡时扣费，扣费金额根据乘客实际额外绕行时间和距离计算。规定当绕行超过10 min，且绕路比超过一定限值时，票价可以抛物线形式降低，但不得低于最低票价。例如当基础票价为8元，最低票价为2元，绕路比超过0.05(5%)时，实际票价与绕路比的函数关系如图2所示，其中抛物线部分函数关系如式(3)。

图2 票价与绕路比关系图

(2)

式中：为第站上车乘客数；为第站上车的实际票价。

=-2 400(20·-1)·(-120)+8

(3)

该式由过点(，2)且顶点为(0.05，8)的抛物线顶点式建立。代表乘客能够忍受的最大绕路比。本文经过调研得到的为0.12，即乘客能够接受的最大绕路比为12%。式中，为第站上车实际票价，为绕路比，计算公式为

=-1

(4)

式中：为第站上车实际行驶路程；为第站上车只停靠固定站点的路程。相应绕行时间即为实际行驶路程与只停靠固定站点的路程之差与公交平均车速(两种情况平均车速设定为相同)的比值。

2.1.2 额外运营成本

由于响应乘客预约导致车辆偏离原行驶路线，必定造成车辆运营成本增加，额外运营成本与车辆每公里运营成本的关系如下：

(5)

2.2 目标函数F2

目标函数主要由响应预约导致车上乘客增加的乘坐时间(h)、响应预约导致其他站点乘客增加的等待时间(h)、预约被响应乘客减少的等待时间(h)、不响应乘客预约导致该乘客增加的等待时间(h)构成：

=-(++)

(6)

在的计算中设置时间窗约束作为判断条件。若为响应某站点(设为)预约导致绕路且该站点的行驶时间未超过发车的间隔时间，则安排当前车辆绕路到该站点去接预约乘客，此时取；否则不安排当前车辆绕路到该站点，此时取，即乘客等待下一趟车的时间成本更优。无论取或，的计算公式不变。其中，为响应预约而导致绕路行驶的时间为

=(-)

(7)

式中：为停靠第站导致的绕路行驶时间；为停靠第站的行驶路程；为不停靠第站的行驶路程；为公交平均车速。

1) 车上乘客增加的乘坐时间(h)。由于响应其他预约导致车上原有乘客增加的乘坐时间为

(8)

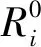
2) 其他站点乘客增加的等待时间(h)。由于响应预约导致其他站点乘客增加的等待时间为

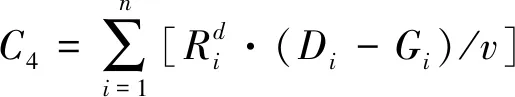
(9)

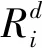
3) 预约被响应乘客减少的等待时间(h)。若本班次不响应该乘客预约，系统默认安排下一班次车辆响应，即该乘客需要多等待一个发车间隔的时间，才能等到下一班次车辆到达。因此本次预约被响应乘客减少的等待时间为

(10)

4)不响应乘客预约导致该乘客增加的等待时间(h)。与含义类似，若本班次不响应该乘客预约，该乘客需要多等待一个发车间隔的时间。因此不响应乘客预约导致该乘客增加的等待时间为

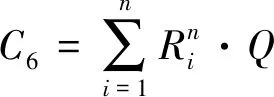
(11)

2.3 模型求解

决策模型的求解分发车前收到预约和发车后收到预约两种情况。

2.3.1 发车前收到预约

收集所有在发车前收到的预约，调度系统将集中一次性处理，应用遗传算法得到一条使乘客及公交公司收益最优的路线，并将决策结果回复给所有预约乘客。应用遗传算法求解首先需要应用一定方法使得问题的所有解映射到一个染色体集合。由于该问题中，对于某个站点只有停靠与不停靠这两种情况，因此可以用一串二进制编码作为染色体，1代表停靠，0代表不停靠，染色体长度即为所有站点个数。具体遗传算法求解过程如下：

1) 对每个站点是否停靠的规划对应一条染色体，随机生成条染色体。

2) 约束站点。规定固定站点必停，上一班次调度中未响应的预约站点必停。

3) 对条染色体计算和两个目标函数值。

4) 对条染色体采用非支配排序和拥挤度计算选择2条。

5) 通过选择、交叉、变异得到2条子代。

6) 对2条子代再次计算新的和目标函数值。

7) 将条父代与2条子代种群合并，共得到3/2条染色体，对每条染色体计算其非支配度和拥挤度，并按非支配度等级由高到低排序，对于非支配度等级相同的按拥挤度由高到低排序。

8) 通过精英选择策略从7)中的3/2条染色体中筛选出条染色体。

9) 循环进行步骤3)～8)100次。

10) 在非支配度等级最高的种群中，是效益，不存在约束，即越大越好。存在时间约束条件，若取，则选择值最大的染色体作为决策结果；若取，则选择当前种群中的第一条作为决策结果。

11) 反馈预约结果。染色体决策结果中为1的站点则表示当前班次响应，回复预约乘客按规定时间到达站点乘车；为0的站点则该班次不停靠，回复预约乘客下班次响应，并提供下班次发车时间。

2.3.2 发车后收到预约

若车辆在运行过程中收到乘客预约信息，决策模块首先需判断该乘客预约站点与车辆当前所处位置的关系。若预约站点在车辆行驶方向前方，则对该预约分别计算响应与不响应对应的两个目标函数，响应记为与，不响应记为与，若>且取则响应该预约，否则不响应；若预约站点在车辆行驶方向后方，则由下一班次响应预约。默认已决策回复过的预约结果不变。

3 案例分析

为验证模型有效性，本节方案随机选取了19个站点，其中固定站点4个，柔性站点15个，部分坐标见表1。

表1 站点坐标(站点所在地理位置)表

固定路线为只停靠表1中4个固定站点的行车路线，行驶路径站点序号为1-7-13-19。模拟乘客预约部分信息见表2中的两个方案，表中接收预约时间表示从发车时刻开始到收到预约的时间，0 h表示发车前收到的预约请求。公交模型运行基本参数为：平均车速20 km/h，基础票价8元，车辆每公里运营成本6元，发车间隔0.5 h。其中智能公交调度方案一由于车辆实际行驶路线未达到可变票价标准，因此所有预约被响应乘客的实际票价为基础票价8元不变。站点及线路如图3所示。

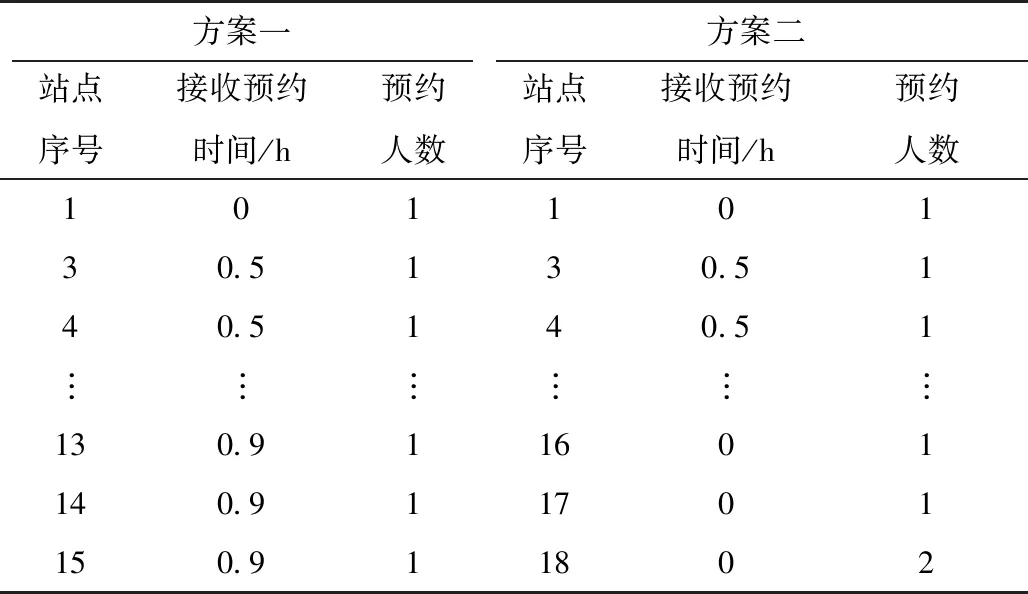
表2 动态预约表(方案一/方案二)

图3 站点及线路图

将表1和表2的参数代入前述计算模型中，借助MATLAB对该模型进行计算，得到各方案的参数见表3。其中方案一对应的线路终解BestS=1011011110011010001，该编码表示行驶路径站点序号为1-3-4-6-7-8-9-12-13-15-19；方案二对应的线路终解BestS=1011011110011111011，该编码表示行驶路径站点序号为1-3-4-6-7-8-9-12-13-14-15-16-18-19。图3结果表明，通过优化求解后实现了车辆经过多个柔性站点，搭载乘客数相比固定站点路线有明显增加。相比于固定路线行驶，方案一、方案二对应的公交路线使票价收入由24元分别增加至88元和158.48元，票价收益分别增加64元和134.48元。虽然智能公交路线因绕路导致额外运营成本有所增加，但最终的总收益相比固定路线依然有所提高，由24元提高到61.29元和102.18元。根据表3中～参数可见，虽然绕路导致和有所增加，但缩短了预约站点乘客的等待时间以及降低了拒载的乘客人数，最终也由固定路线的-5 h提高到0.79 h和-0.94 h(为负或正值表示所有乘客的总耗费或总节省的时间)。最终实现公交公司运营收益与所有乘客的总时间收益的共同增加。

方案一和方案二的柔性调度使搭载乘客人数比固定路线人数有所增加，实现了降低车辆空载率的目的，也实现了运营收益和总时间收益优化。另外，与方案一相比，方案二的行驶路径更长，进而导致部分乘客的实际票价有所降低，见表4，说明当智能公交绕行时间和绕路比满足一定条件时，实际票价可随着绕路比的增加而降低，以此来提高乘客的乘坐意愿和满意度。

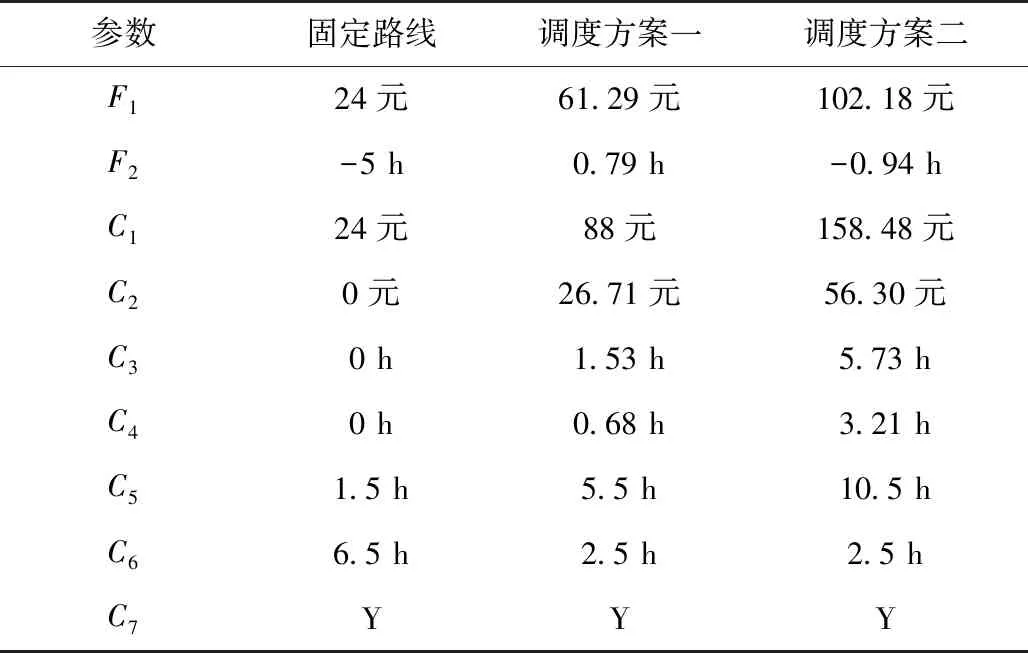
表3 智能公交调度方案与固定路线行驶方案各项参数对比

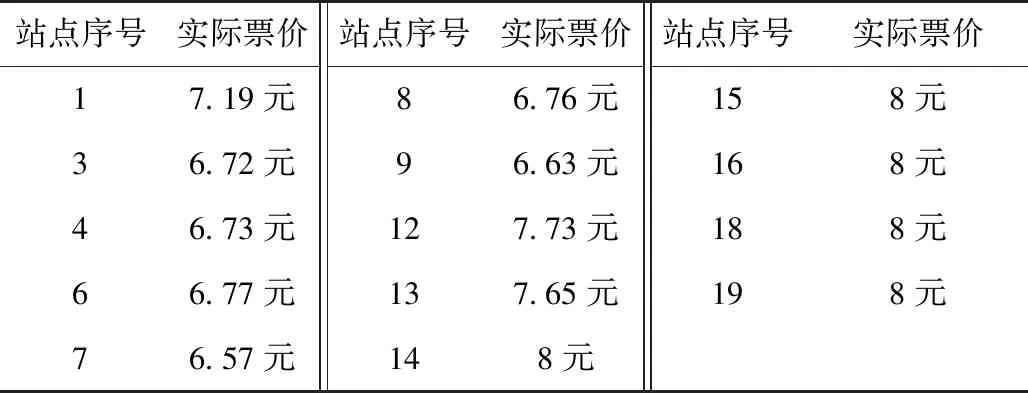
表4 方案二中各停靠站点实际票价

4 结束语

本文提出一种可变票价的智能公交调度系统，该系统中公交票价随绕路比变化，在一定程度上补偿了时间成本增加的乘客，提高乘客的乘坐意愿和乘坐满意度。建立公交公司收益和乘客整体少等待时间两个目标函数，应用遗传算法进行求解，决策车辆的最优行驶路径。通过实际算例分析结果可得，该智能公交调度系统相对于传统固定路线运营模式，能有效提高公交公司的收益并减少乘客的整体等待时间。