融合正余弦优化与跳距优化的DV-Hop定位算法*

张 晶，贺媛媛

(1.昆明理工大学信息工程与自动化学院，云南 昆明 650500；2.云南枭润科技服务有限公司，云南 昆明 650500；3.昆明理工大学云南省人工智能重点实验室，云南 昆明 650500；4.昆明理工大学云南省计算机技术应用重点实验室，云南 昆明 650500)

1 引言

无线传感器网络WSN(Wireless Sensor Network)是由无规律散落的节点组成的不规则监测区域，大多应用于动态追踪、环境监测和森林火灾预警等多种学科交叉的相关领域[1]。在整个网络区域中，各个节点采用无线通信技术进行数据处理和传输，实现节点之间的信息交互并达到对目标空间范围的监测。

随着无线传感器网络定位研究的不断深入，节点不仅需要进行数据收集，更需要精确获知节点的位置信息。因此，准确获取事件发生的位置是无线传感器网络最主要的功能之一，未知节点的定位研究具有不可或缺的重要性。但是，在实际环境中，节点部署[2]不均匀、复杂的传播环境等相关问题随时存在，因此对定位算法的性能提出了更高的要求。

在当前规模化通信网络中，存在随身配置GPS的锚节点和无法明确位置的未知节点，但由于高输入高输出的成本与能耗，相比于未知节点而言，锚节点的数量[3]非常有限，因此无法将锚节点大量应用于功耗小、成本低的网络中。

目前的定位算法根据节点是否需要实际测量其之间的距离分为2种类别：一种是需要给传感器附加额外装置[4]来获取节点之间的间距，这种算法被称为测距算法，其定位结果相对来说更精准。但是，由于需要添加额外[5]的硬件设备，使得算法的部署对节点成本的要求较高,不适合大型区域的监测[6]。另一种类别是不需要添加任何其他硬件设备，只需要网络之间能够通信即可的非测距算法[7]。这种算法定位精度低，但由于其相对测距算法而言节点造价低，适合大型传感网络监测，成为近些年研究的热点。本文要探讨的就是无需测距算法中的典型算法DV-Hop。

DV-Hop定位算法是一种较为传统的传感器节点定位算法，该算法的测距原理为：首先由网络中各锚节点通过洪泛方式广播自身路由信息，直至其通信范围内各未知节点均获取自身到锚节点的最小跳数信息[8]；之后再得出平均跳距信息，将二者相乘得到两点之间的距离，再用极大似然或三边测量估算目标节点的位置。但是，该算法存在一个缺陷，即当最小跳数大于1跳时，由于锚节点的平均跳距本身在计算的时候就存在误差，所以导致未知和已知节点之间的距离存在更大的误差。

针对DV-Hop定位算法中跳距计算不精确以及最小二乘法求解不能达到最优无偏状态导致对无线传感器网络中未知节点定位不准确，本文提出了一种融合正余弦优化与跳距优化的DV-Hop定位算法。基本思想是：首先选取每个未知节点周围所有锚节点中平均跳距最小的锚节点作为最优化锚节点；然后选取其余任一锚节点与未知节点构成三角形，将最优化锚节点到未知节点的边作为三角形中的最优化边；其次利用余弦定理计算其余锚节点到未知节点的距离达到优化跳距的目的；最后利用正余弦优化算法改进最小二乘法，利用正余弦函数的波动性寻找未知节点的最优位置。

2 DV-Hop定位算法及改进算法

2.1 DV-Hop定位算法

传统的DV-Hop定位算法依赖于网络连通性，首先由网络中各锚节点通过洪泛方式广播自身路由信息，直至其通信范围内各未知节点均获取自身到锚节点的最小跳数信息；之后再得出平均跳距，将二者相乘得到两点之间的距离，再用极大似然或三边测量估算目标节点的位置。DV-Hop定位算法步骤如下所示：

(1)获取最小跳数。

整个网络中的锚节点通过洪泛的方式广播自己的分组信息，每个未知节点会收到来自多个锚节点广播的数据包，数据包Xdatai包含第i个(1≤i≤n)锚节点的ID、自身到未知节点的跳数Hop及其位置坐标，如式(1)所示，多个数据包组成一个更大的集合{Xdata1,Xdata2,…,Xdatan}。

Xdatai={ID,Hop,(xi,yi)}，i=1,2,…,n

(1)

其中，Hop初始值为0。当接收方接收锚节点信息时，优先选择相比之下较小跳数的分组，忽略其他分组，依次继续转发并将跳数值按规律加1。

(2)记录未知节点与锚节点的跳距值。

将所有锚节点的位置坐标对应相减再开平方后的总和与所有锚节点的跳数之和相除得到如式(2)所示的平均跳距，再将锚节点到未知节点的跳数与平均跳距相乘得到跳距值，如式(3)所示：

(2)

di=HopDistancei×hopi

(3)

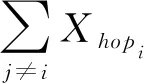
(3)估计目标节点位置。

当锚节点数大于或等于3时，使用最小二乘法估计目标节点位置，计算方法如式(4)～式(9)所示：

(4)

其中，(x,y)为未知节点位置坐标，所有锚节点(x1,y1),…,(xn,yn)到未知节点的跳距用d1，d2，…，dn表示。

然后用前n-1个方程减去最后一个方程，得到如式(5)所示的方程组：

(5)

再将式(5)进行拆分，转化为矩阵A、B和X，得到AX=B的形式，如式(6)～式(9)所示：

(6)

(7)

(8)

(9)

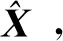
2.2 DV-Hop改进算法

针对传统DV-Hop定位算法存在的不足，文献[9]提出了一种增强DV-Hop定位算法，通过加权系数[9]设定阈值赋予锚节点权重值的方式降低定位误差。但是，如果锚节点与未知节点间存在多跳时，距离较远会导致锚节点被忽略，通过加权系数也无法降低误差值。文献[10]提出一种基于修正平均跳数的DV-Hop定位算法，该算法在修正分数跳数和锚节点的平均跳距得到的跳距值的基础上使用改进后的差分进化算法DE(Differential Evolution)估计目标节点位置。但是，DE算法类似于遗传算法，需要的参数较多，增加了算法计算复杂度，同时受到缩放因子和交叉概率的制约，收敛速度变慢，不利于收敛到全局最优[10]。文献[11]在求最值的过程中利用梯度算法进行求解,通过多边定位获取目标节点估计位置，将该估计位置作为L-M(Levenberg-Marquard)优化算法的初始值，之后进行迭代求精,但受到相关函数复杂性和参数个数的条件限制，定位精度也会变低[11]。文献[12]提出的优化算法是设置跳数阈值，根据锚节点的位置信息修正跳距，采用质心算法和最小二乘法[12]估计位置坐标。文献[13]提出一种基于跳距重估算法，该算法首先对跳距进行评估，然后通过计算修正系数来修正最小跳数，最后使用最小二乘法估计节点位置[13]。但是，现有的改进算法并没有很好地修正跳距值和降低定位误差，因此本文在修正跳距以及最小二乘法求解上进行优化。

3 本文改进算法

上述改进的DV-Hop定位算法虽然在一定程度上能够提高定位精度，但在现实情况中，锚节点和未知节点之间的距离仍然存在误差。在最小二乘法中，未知节点与各锚节点间距离的计算方法均会产生一个误差值，所有误差值之和构成该未知节点定位误差值，结合函数求导规则计算得出该未知节点定位误差极小值，而并非其最小值，从而使得该计算结果陷入局部最优，导致节点定位[14]精度低。为此，本文提出一种融合正余弦优化与跳距优化的DV-Hop定位算法。其基本思想是：首先选取每个未知节点周围所有锚节点中平均跳距最小的锚节点作为最优化锚节点；然后选取其余任一锚节点与未知节点构成三角形，将最优化锚节点到未知节点的边作为三角形中的最优化边；其次利用余弦定理计算其余锚节点到未知节点的距离达到优化跳距的目的；最后利用正余弦优化算法改进最小二乘法，利用正余弦函数的波动性寻找未知节点的最优位置。正余弦优化算法仅需设定1个参数，无需额外调参，从而降低了算法计算复杂度，且内置随机因子可灵活控制粒子的移动范围，避免使其陷入局部最优。相比其他改进算法而言，该算法有效提高了定位精度。

3.1 选取最优化锚节点

由于未知节点到锚节点之间的距离存在误差，因此本文提出最优化锚节点的概念。最优化锚节点为每个未知节点到锚节点的距离[15]能够达到最优且使得两点之间的距离误差最小的锚节点，即平均跳距最小的锚节点。由于每个未知节点最近的锚节点的跳距信息是通过所有锚节点计算出来的，所以最近锚节点的平均跳距信息有可能不是最小平均跳距，因此选取最优化锚节点的优势如下：

如图1所示，A是未知节点，L1,L2和L3是锚节点，由DV-Hop算法可知，L1L2和L1L3长度分别为40 m和100 m，最小跳数分别为2和5，根据式(2)，得L1,L2和L3的平均跳距分别为20 m,24 m和22.5 m，AL1,AL2和AL3的长度分别为：3*20=60 m，2*24=48 m，3*22.5=67.5 m。按照选取最近的锚节点的平均跳距来优化其他锚节点与未知节点的距离，得到如下结果：根据A到各个锚节点的距离可知，L2是最近的锚节点，用L2到A的距离作为A与其他锚节点构成的三角形中的最优化边，使用余弦定理修正得到L1到A的距离为66.2 m，L3到A的距离为98.6 m。按照选取的最优化锚节点得到如下结果：根据A到各个锚节点的距离可知，L1是最短平均跳距的锚节点，用L1到A的距离作为A与其他锚节点构成的三角形中的最优化边，使用余弦定理修正得到L2到A的距离约为40.0 m，L3到A的距离约为80.0 m。通过比较AL1,AL2和AL3可以明显看出,改进锚节点选取方式后，优化了锚节点与未知节点间的距离。

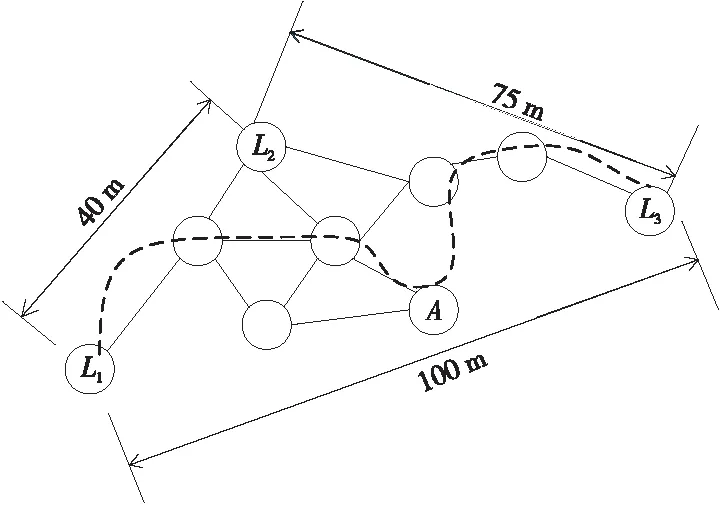
Figure 1 DV-Hop schematic diagram

如图2所示，选取最优化锚节点后使用余弦定理修正的基本思想如下所示：

(1)首先在MA1,A1A2和MA2各边跳数已知的情况下，使用3边的跳数信息近似代替距离信息，得到角度θ1：

(10)

其中，Hop1是最优化锚节点与未知节点的跳数，Hop2是最优化锚节点和其余锚节点中任意一个锚节点的跳数，Hop3是未知节点和其余锚节点中任意一个锚节点的跳数。

Figure 2 Schematic of anchor node using minimum hop

(2)锚节点A2、A3之间的距离dA2A3可以通过位置坐标对应相减再开平方计算得到。使用最优化锚节点的最短跳距乘以M到A2的跳数得到dMA2，再利用式(10)得到的θ1可以计算出dMA3：

dMA2≈Hop1×HopDistanceA2

(11)

(12)

HopDistanceA2是根据式(2)得出的平均跳距。当3条边无法构成三角形时，即Hop1+Hop2≤Hop3或Hop1-Hop2≥Hop3时，

dMA3≈Hop1×HopDistanceA3

(13)

就使用传统DV-Hop算法中锚节点平均跳距与对应跳数相乘的计算方式，但此时基于最优化锚节点自身的优势，因此用每个最优化锚节点的平均跳距[16]代替每个未知节点周围其余锚节点的平均跳距，再利用余弦定理进行修正，达到优化跳距的目的，降低对未知节点的定位误差。

3.2 正余弦优化算法

(14)

(15)

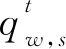
(1)r1表示下一个解所在区域，位于最优解和当前解的内部或者外部，迭代次数的多少决定了r1的大小，为了使局部开发能力和全局探索能力达到平衡，r1会随迭代次数逐渐减小。

(2)r2是[0,2π]的随机数，其定义了正余弦波动范围，决定个体的移动方向，同时表明当前解是靠近或远离目标解。

(3)r3是[0,2]的随机数，决定目标位置的随机权重，若r3>1，表明需要增强目标解[18]对当前解的牵引影响;若r3<1表明需要削弱目标解对当前解的牵引影响，防止陷入局部最优。

(4)r4是[0,1]的随机数，决定选择正弦函数还是余弦函数。

以图3为例说明正弦函数和余弦函数对式(14)中个体位置更新的影响，正弦函数和余弦函数的循环模式允许将一个解重新定位到另一个解的范围内，这样可以充分利用2个函数计算结果之间的空白区域。为了探索搜索空间，本文通过改变正弦函数和余弦函数的范围来实现。正弦函数和余弦函数的值域是[-1,1]，但是在函数搜索过程中，为了加大寻优能力，增加了一个乘子2来调大振幅，使得当余弦函数变量取值为π时以及正弦函数变量取值为3π/2时,函数返回值为-2; 当余弦函数变量取值在[0,2π]以及正弦函数变量取值为π/2时,函数返回值为2，这样可以更加有效地进行波动搜索。图3所示是SCA寻优过程，改变正弦函数和余弦函数变量的取值，可以更新解的位置，当正弦函数或余弦函数返回值在[-1,1]时，候选解可以较好地搜索具备前景的空间；当正弦函数或余弦函数返回一个大于1或小于-1的值时，候选解可以在探索所定义的搜索空间之外的区域进行全局搜索。SCA使用特定空间区域范围中的余弦函数和正弦函数，可以顺利地从探索阶段过渡[19]到开发阶段；优化过程中,由于最优解的多可能性和不缺失性,候选解在当前最优解周边更新其位置，并继续搜索整个空间中的最优区域。

Figure 3 Optimization process of sine and cosine optimization algorithm

3.3 本文改进算法步骤

Step1首先根据传统DV-Hop定位算法已经得到的跳数和平均跳距，找出每个未知节点周围所有锚节点中平均跳距最小的锚节点，即最优化锚节点。

Step2根据最优化锚节点、未知节点、其余任一锚节点相互之间的跳数信息，利用余弦定理得到最优化锚节点和其余任一锚节点之间的角度。

Step3根据步骤2得到的角度信息，重新利用余弦定理得到其余任一锚节点与对应未知节点修正后的距离。

Step4考虑特殊情况，即构不成三角形的情况，利用式(13)代替要修正的边的距离。

Step5利用正余弦优化算法(SCA)进一步优化。

(1)初始化种群规模N，在[0,100]内随机生成N个解，并且随机设定各个解的初始位置。

(2)根据初始解位置，计算相应的f(x)值。

(3)在每一代更新位置信息，重新计算每个解和本次全局的f(x)值。

(4)比较更新后所有解的f(x)值，若当前解大于最优解，就更新全局最优解位置。

(5)判断是否满足终止条件，是则输出当前最优解，即未知节点最优估计位置坐标，否则重复步骤(2)～步骤(4)。

4 仿真模拟

为了验证本文算法的可行性和有效性，在Matlab 2019a上对本文改进算法、文献[12]算法、文献[13]算法和DV-Hop定位算法进行仿真模拟，得到以下4幅图：图4是网络节点分布图,图5是锚节点均匀变化下的平均误差图，图6是通信半径均匀变化下的平均误差图,图7是节点总数均匀变化下的平均误差图。实验过程和结果分析如下所示：

所有节点无规律地散落在100 m*100 m的区域内,节点的平均定位精度用式(16)来计算：

(16)

其中，(x,y)表示未知节点真实位置坐标，(xg,yg)表示未知节点的估计位置坐标，n表示节点总数。

Figure 4 Network node distribution

首先，在100 m*100 m的区域内，通信半径R为40 m，节点总数为200个，锚节点在节点总数中所占比例由0.1到0.5间隔0.05进行变化，循环100次取平均值,得到如图5所示的结果。分别选取锚节点比例为0.1，0.3，0.5进行对比。当锚节点比例为0.1时，Error_accuracy：本文改进算法为6.037，文献[13]算法为7.659,文献[12]算法为9.714,DV-Hop定位算法为11.03，本文改进算法相比其他对比算法分别优化提升了1.288,3.343和4.659；当锚节点比例为0.3时，Error_accuracy：本文改进算法为3.405,文献[13]算法为5.032,文献[12]算法为7.281,DV-Hop定位算法为10.220，本文改进算法相比其他对比算法分别优化提升了1.627,3.876和6.815；当锚节点比例为0.5时，Error_accuracy：本文改进算法为2.774，文献[13]算法为3.825,文献[12]算法为6.144,DV-Hop定位算法为10.570，本文改进算法相比其他对比算法分别优化提升了 1.051,3.370和7.796。由此可见在锚节点数均匀变化的过程中，相比于其他3种算法，本文改进算法平均定位误差最小，定位精度最高。

Figure 5 Average positioning error under uniform change of anchor nodes

其次，在100 m*100 m的区域内,节点总数为200，锚节点数为50，通信半径R由30 m到60 m间隔5进行变化，循环100次取平均值，得到如图6所示的结果。分别选取R为30 m,45 m,60 m进行对比。当R=30 m时，Error_accuracy：本文改进算法为3.382,文献[13]算法为4.819,文献[12]算法为6.552,DV-Hop定位算法为8.567，本文改进算法相比其他对比算法分别优化提升了1.437,3.170和5.185；当R=45 m时，Error_accuracy：本文改进算法为3.708,文献[13]算法为5.523,文献[12]算法为7.700,DV-Hop定位算法为12.09，本文改进算法相比其他算法分别优化提升了1.815,3.992和8.382；当R=60 m时，Error_accuracy：本文改进算法为4.754,文献[13]算法为6.636,文献[12]算法为8.823,DV-Hop定位算法为15.100，本文改进算法相比其他算法分别优化提升了1.882,4.069和10.346。观察4种定位算法，通信半径在均匀变化的过程中，随着通信半径的增大，整个网络中的节点跳数也在增加，导致每种算法的距离误差呈现增长趋势。由此可见，虽然4种算法误差都普遍增长，但是本文改进算法的平均定位误差最小，增长幅度也最小，定位精度最高。

Figure 6 Average positioning error under uniform change of communication radius

最后，在100 m*100 m的区域内，固定通信半径R为40 m，锚节点数为50，节点总数由100到400间隔50进行变化，循环100次取平均值，得到如图7所示结果。分别选取节点总数为100,250,400进行对比。当节点总数为100时，Error_accuracy：本文改进算法为4.510,文献[13]算法为6.373,文献[12]算法为8.568,DV-Hop定位算法为10.870，本文改进算法相比其他对比算法分别优化提升了1.863,4.508和6.360；当节点总数为250时，Error_accuracy：本文改进算法为2.975,文献[13]算法为4.495,文献[12]算法为6.963,DV-Hop定位算法为10.880，本文改进算法相比其他算法分别优化提升了1.520,3.988和7.905；当节点总数为400时，Error_accuracy：本文改进算法为2.433,文献[13]算法为3.769,文献[12]算法为5.759,DV-Hop定位算法为11.110，本文改进算法相比其他对比算法分别优化提升了 1.336,3.326和8.677。观察4种定位算法，在固定锚节点数和通信半径的情况下，当锚节点数不断增加时，与其他算法相比，本文改进算法平均定位误差最小，定位精度最高。

Figure 7 Average positioning error under uniform change of total number of nodes

5 算法复杂度分析与评估

本文所提算法的复杂度与网络区域中节点总数的变化以及算法内部循环语句迭代次数有关。传统DV-Hop定位算法和文献[12，13]所提出的改进算法中，在均未使用智能优化算法的情况下，其算法复杂度均为O(n2)，而本文使用正余弦优化算法，在计算算法复杂度时需要一定的参数支撑，其中节点总数为n，锚节点所占比例为p，最大迭代次数为TMAX，种群规模为N，设置频度函数T(n)=(1-p)·n·TMAX·N,可以得到本文算法的复杂度为O(n3)。在本节中代入实际的数值来计算复杂度，规定节点的通信半径为40 m，锚节点比例为0.2，迭代次数为100次，种群规模为100，节点总数为100，此时各算法的复杂度与定位精度如表1所示。

从表1可以看出,传统DV-Hop定位算法和文献[12,13]算法，在没有使用智能优化算法的前提下，算法的复杂度均为O(n2)，且文献[12,13]算法的定位精度比传统DV-Hop定位算法分别提高了2.302和4.497，而本文算法的复杂度为O(n3)，算法复杂度虽不占优势，但定位精度比传统DV-Hop定位算法和文献[12,13]算法分别提高了6.360，4.058和1.863。综上，本文虽使用了正余弦优化算法，导致算法复杂度在一定程度上有所增加，但是在定位精度上比其他对比算法都有所提高，定位误差相对较小，效果明显。

Table 1 Comparison of algorithm complexity and positioning accuracy of four algorithms

6 结束语

本文改进算法中定义了最优化锚节点的概念，利用余弦定理修正锚节点和未知节点之间的距离，之后再用正余弦优化算法(SCA)改进最小二乘法来估计目标节点位置。正余弦优化算法(SCA)由于仅需要1个参数，很大程度上避免了调参的繁琐,提升了算法的性能且易达到全局最优，在设置随机参数和递减参数的过程中，使得算法中探索和开发2个阶段的能力能够达到很好的平衡，有效降低了定位误差。实验结果显示，不论锚节点、通信半径和锚节点数等限制条件如何变化，本文提出的融合正余弦优化与跳距优化的DV-Hop定位算法都比传统DV-Hop及其改进算法的定位误差更小。但是，正余弦优化算法(SCA)局部搜索能力较弱且只能迭代寻优，是该算法的缺陷，因此应该对其进行改进，例如通过使用混沌算子策略提高初始种群的质量以达到减少迭代次数的效果；随后采用高斯震荡算子提升算法的局部寻优能力，以提高算法的整体效率。基于对本文算法优缺点的整体分析，在今后的研究中会着重研究如何进一步提升算法的性能与效率。