基于概率评估差分进化的多峰值优化

王子佳，詹志辉

（1.广州大学 计算机科学与网络工程学院,广东 广州 510006;2.华南理工大学 计算机科学与工程学院,广东广州 510006）

许多实际优化问题中具有多个全局最优解，如蛋白质结构检测[1]、电磁系统设计[2]、结构优化[3]和多行人检测[4-6]等。例如，多行人检测通常要求算法在一张给定的图片中尽可能多地检测到多个行人。此类问题被称为多峰值优化问题。求解多峰值优化问题具有很多实际益处。如果能同时找到一个实际问题的多个最优解，就能用多种方式来保持系统的最优性能。当其中某个最优解因为实际物理条件无法实现时，可以很快地切换到另一个最优解。

演化算法[7-14]因其基于种群的进化机制，拥有多个候选解，在求解多峰值优化问题中具有潜在的优势。然而，传统的演化算法仅仅是寻求问题的一个最优解。为了求解多峰值优化问题，最主流的思想便是小生境策略[15-28]，就是将整个种群划分为多个子种群，如Crowding[15]、Speciation[16]、聚类[17-18]、Hill-valley[23]等。但是，现有的小生境策略对它们各自的小生境参数特别敏感，以及为了提升种群划分的准确性，算法需要采样并评估足够多的中间点，消耗了大量的适应值评估次数(fitness evaluations,FEs)。

在我们先前发表于IEEE Transactions on Cybernetics 的研究中[29]，提出了一种自适应分布估计的差分进化算法(adaptive estimation distribution distributed differential evolution,AED-DDE)，算法提出了一种基于自适应分布估计(adaptive estimation distribution，AED)的无参数小生境策略，并提出了概率局部搜索机制(probabilistic local search，PLS)来提升算法求解精度。AED-DDE 算法在多峰值优化问题上已经取得了很好的实验效果。然而，如何在极其有限的适应值评估次数内找到问题的多个全局最优解，依然为AED-DDE 以及其他演化算法带来了巨大的挑战。如果可以分析个体的历史更新经验，对个体进行选择性评估，减少算法运行过程中无效或低效的适应值评估，算法性能将会得到进一步的提高。

本文基于之前AED-DDE 的工作，进一步提出了概率评估机制(probabilistic evaluation,PE)，并将这个机制应用在AED-DDE 算法中，称为PEDE。在PEDE 算法中，每个个体会通过历史经验的学习，被赋予第一层的适应值评估概率，并根据该个体的适应值赋予第二层的适应值评估概率。每个个体在进化过程中会根据该个体的双层适应值评估概率进行选择性评估。被评估的个体更新个体的适应值，同时学习这个更新过程来调整自身的适应值评估概率；而未被评估的个体则直接根据该个体的历史经验进行个体更新。通过概率适应值评估机制，可以节省FEs 来增加算法的迭代次数，从而提升算法求解精度。同时，通过概率评估机制，可以充分学习到个体的历史经验，更加方便种群的搜索。

在多峰值优化测试集IEEE CEC 2013 上的实验结果显示，相比于其他的多峰值优化算法，PEDE算法取得了更好的实验结果。同时，将概率评估机制应用到了其他基于DE 的多峰值优化算法中，算法效果都有了一定的提升。

1 相关工作

1.1 差分进化算法

差分进化算法(differential evolution，DE)最初是由Storn 和Price 提出[30]。它通过群体内个体之间的差异来优化群体的搜索方向。DE 算法在进化过程中有变异、交叉、选择等操作，具体来说：

1)变异

在每一代中，每个个体xi称为目标向量，它通过变异操作产生它自身的变异向量vi。3 种常用的变异策略如式(1)～(3)所示：

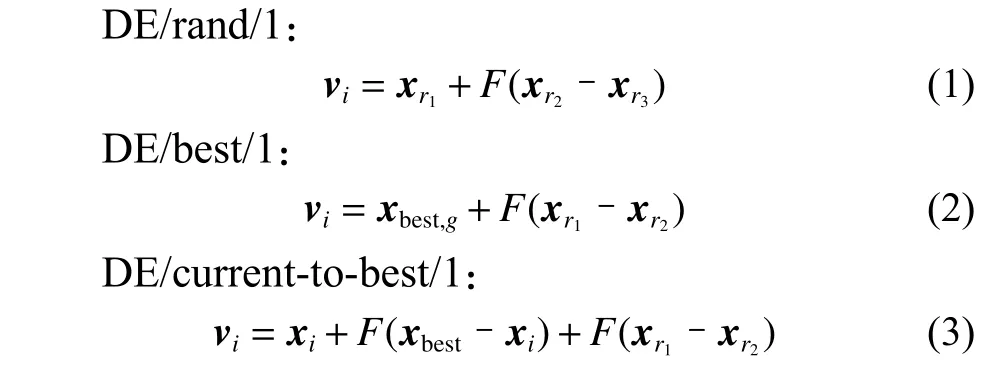
其中，r1、r2和r3是3个不同的{1,2,…,N}中的整数(N代表种群规模)，并且都与i不同。放大系数F是一个正实数的控制参数，用来放大差分向量。xbest是指当前种群中适应值最好的个体。

2)交叉

在变异操作后，DE 通常会在个体xi和它自身的变异向量vi上执行二元交叉操作，来产生试验向量ui，如式(4)所示：

其中，jrand是{1,2,…,D}中的一个随机整数(D代表问题维度)，用来保证试验向量ui至少有一维不同于xi。参数CR 是交叉概率，用来决定试验向量ui从变异向量vi的继承比例。

3)选择

为了判断试验向量ui是否可以进入下一代，试验向量ui会与个体xi进行比较。其中拥有较好适应值的个体进入下一代。例如，对于一个最大化问题来说，拥有较大适应值的个体会进入下一代，如式(5)所示：

其中f(x)为适应值评估函数。

而在多数基于DE 的多峰值优化算法中，普遍使用的选择操作是将试验向量ui与距离ui最近的个体xj进行比较，拥有较好适应值的个体进入下一代，如式(6)所示：

1.2 多峰值优化算法

在求解多峰值优化问题中，最主流的思想便是小生境策略[15-28]，就是将整个种群划分为多个子种群，每个子种群分别去寻找该问题的一个或多个全局最优解，如Crowding[15]、Speciation[16]、聚类[17-18]、Hill-valley[23]等。但是，现有的小生境策略对它们各自的小生境参数特别敏感，以及为了提升种群划分的准确性，算法需要采样并评估足够多的中间点，消耗了大量的FEs。

基于小生境策略，Zhang 等[19]提出了一种基于局部敏感哈希的小生境技术用来减小算法运行过程中的计算复杂度。Zhao 等[20]提出了基于局部二值模式的小生境技术，并设计了一种参数自适应的DE 算法。Chen 等[21]设计了一种基于个体的分布式框架，在每个个体周围产生虚拟个体来形成小生境。Wang 等[22]设计了一种基于最小生成树拓扑结构的差分进化算法，充分捕捉个体进化过程中的全局信息和局部信息。此外，Wang等[24]还设计了一种基于AP 聚类的无参小生境技术，在避免了小生境参数敏感度的同时，也免去了FEs 的消耗。

除了研究小生境策略，许多研究人员尝试提出新的变异策略来提升多峰值优化算法的性能。Biswas 等[25]提出了基于局部信息分享机制的DE算法(local information DE，LoICDE 和LoISDE)。同时，Biswas 等[26]进一步提出了基于邻近度和父代中心的DE 算法(parent-centric normalized mutation with proximity-based crowding DE，PNPCDE)，充分利用邻居的进化信息。Wang 等[27]则针对多峰值优化问题中的选择操作，提出了一种基于AP 聚类的概率选择操作技术。

除了DE，还有很多演化算法用来求解多峰值优化问题。例如，在文献[31]中，基于聚类的小生境技术被应用在了分布估计算法中，称之为局部多峰值分布估计算法(locally multimodal estimation of distribution algorithm，LMCEDA 和LMSEDA)。

此外，也有一些研究人员通过使用多目标转化的方法来求解多峰值优化问题。Wang 等[32]设计了一种独特的转化方式，在每个维度上都设计了两个互相冲突的目标，算法称之为(multiobjective optimization for multimodal optimization problem，MOMMOP)。

1.3 AED-DDE

1.3.1 基于AED 的自适应无参小生境技术

AED-DDE 算法提出了一种基于AED 的自适应无参小生境技术，每个个体将找到一个适合该个体本身的小生境大小，并形成一个小生境来寻找一个全局最优解。具体来说，每个个体xi会首先选择距离该个体最近的3个个体来形成一个初始的小生境（个体xi的初始小生境大小Mi设置为3）。接着，算法采用高斯分布来估计该小生境的分布。小生境Ni的分布估计Di如式(7)所示:

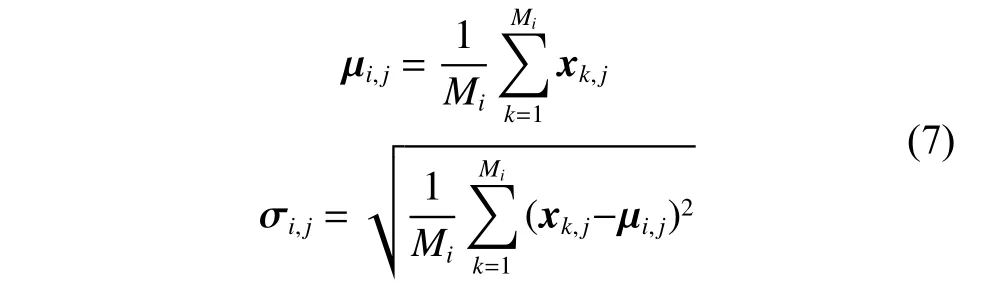
式中：μi和σi表示小生境Ni的各维度均值和方差；xk表示小生境Ni中的第kth个个体；Mi表示小生境Ni的大小（初始化中Mi=3）。

在估计完小生境Ni的分布Di后，AED 使用范围μi±3σi来判断一个给定的个体是否可以被分布Di拟合。算法首先选择距离个体xi第4th近的个体来观察个体是否能落在范围μi±3σi中。如果个体不能落在范围μi±3σi中，这就意味着个体距离个体xi较远。这样，个体应当被小生境Ni排除，小生境Ni应当保持大小Mi=3，从而避免误导进化。

算法1基于AED 的小生境技术

经过基于AED 的小生境技术后，每个个体将找到适合该个体本身的小生境大小，从而自适应地形成多个小生境。不同的小生境协同共进化，执行基本DE 算法的变异和交叉操作来得到试验向量，而后使用式(6)执行选择操作。

1.3.2 基于PLS 的局部搜索技术

为了进一步提高解的准确度，更加精确地找到问题的所有全局最优解，算法提出了概率局部搜索技术(probabilistic local search，PLS)。

在PLS 中，算法使用了基于高斯分布的局部搜索技术，如式(8)所示:

式中：xnew是高斯分布在个体x周围新采样的个体；高斯分布N(x,σ)表示以个体x作为均值，σ作为标准差。标准差σ的设置如式(9)所示：

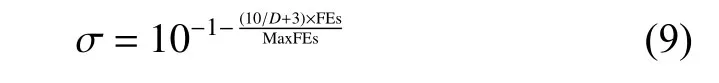
在PLS 中，算法为适应值好的个体分配较高的局部搜索概率。首先，按照个体的适应值对个体进行由坏到好的排序。接着，算法设置第ith个个体执行局部搜索的概率为

式中：ri表示第ith个个体在适应值排序中的位置；N表示种群规模。

在执行局部搜索操作时，每个个体在各自的周围采样2个点。完整的PLS 算法伪代码如算法2 所示。

算法2PLS 算法

2 概率评估的差分进化算法(PEDE)

AED-DDE 算法在多峰值优化问题上已经取得了很好的实验结果。然而，在极其有限的适应值评估次数内，AED-DDE 算法的性能仍然可以进一步提高。本文提出的PEDE 算法基于之前的研究工作AED-DDE[29]，并在AED-DDE 算法的基础上引入了概率评估机制。

2.1 概率评估机制PE

首先，在算法进化过程中，AED-DDE 并没有考虑利用个体的历史进化信息。例如，如果一个个体xj持续被更新，就说明产生的试验向量ui可以经常性地替换个体xj，那么个体xj的适应值很有可能并不好或者处于非最优区域；相反，如果一个个体xj很久没有被更新，就说明产生的试验向量ui很难替换个体xj，那么个体xj的适应值很可能已经非常好或者已经找到了最优解。如果我们可以充分挖掘并利用这些个体的历史进化信息来帮助种群的搜索，算法性能会进一步地提高。

其次，在有限的适应值评估次数内，并没有必要对所有的个体都进行评估。例如，如果一个个体xj持续被更新，就说明产生的试验向量ui可以经常性地替换该个体，那么可以近似认为，在不评估试验向量ui的情况下，试验向量ui的适应值大概率是要好于个体xj的；同样地，如果一个个体xj很久没有被更新，就说明产生的试验向量ui很难替换个体xj，那么我们可以近似认为，在不评估试验向量ui的情况下，试验向量ui的适应值大概率是要差于个体xj的。也就是说，在这两种情况下，可以不去评估试验向量ui，直接利用个体的进化信息就可以近似选择出适应值更好的个体。这个历史经验信息的积累就当作为我们第一层适应值评估概率的基础。

2.1.1 第一层适应值评估概率

首先为每个个体赋予第一层适应值评估概率PFj和两个选择概率PXj和PUj，分别代表个体j的第一层适应值评估概率，选择自身xj进入下一代的概率，以及选择试验向量ui进入下一代的概率，三者均初始化为0.5。

在算法运行初期(在0.3×MaxFEs 内)，需要充分挖掘个体的历史进化信息，因此，在这个阶段里，所有的个体都要进行评估。每当产生一个试验向量ui后，如果试验向量ui的适应值要好于它最近的父代个体xj，则个体xj的选择概率PUj会适当地增加，而选择概率PXj会适当地减小；相反，如果试验向量ui的适应值要差于它最近的父代个体xj，则个体xj的选择概率PUj会适当地减小，而选择概率PXj会适当地增加。我们定义个体xj的选择概率PUj和PXj的范围为[0.2,0.8]，且PUj+PXj=1，二者更新式如(11)所示：

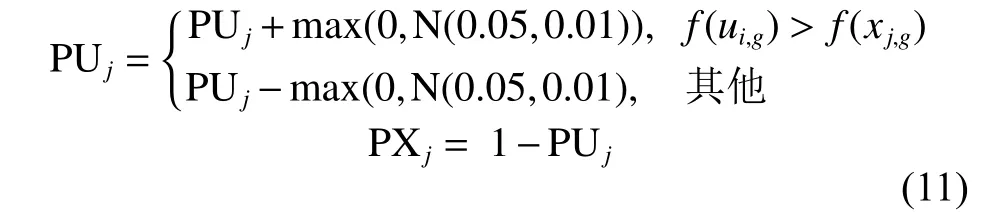
而个体的第一层适应值评估概率PFj则是根据选择概率PUj和PXj，选择二者中的最小值，如式(12)所示：

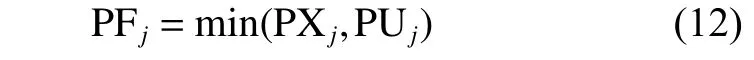
也就是说，假如个体xj的选择概率PUj很大而选择概率PXj很小，那么该个体的第一层适应值评估概率就会设置为PXj，即很小的值。因为xj的选择概率PUj很大，也就是说，根据前期经验，产生的试验向量ui是有很大概率可以替换掉个体xj的，那么即使不对试验向量ui进行评估，也可以近似认为试验向量ui是有很大概率可以替换掉个体xj，故而将个体xj的第一层适应值评估概率PFj设置为较小的值PXj。同理，假如个体xj的选择概率PUj很小而选择概率PXj很大，那么该个体的第一层评估概率就会设置为PUj。因为xj的选择概率PUj很小，也就是说根据前期经验，产生的试验向量ui是几乎不可能替换掉个体xj的，那么即使不对试验向量ui进行评估，我们可以近似认为试验向量ui是几乎不可能替换掉个体xj，故而将个体xj的第一层适应值评估概率PFj设置为较小的值PXj。很显然，个体的第一层适应值评估概率PFj的取值范围就是[0.2，0.5]。

PFj的取值越大，则说明个体xj前期的适应值评估经验越弱，选择概率越模糊。当PFj=0.5时，也就是个体xj前期的适应值评估经验几乎为0，此时如果仍然依赖个体xj前期的适应值评估经验，很有可能误导种群的进化。也就是说，我们希望当PFj=0.5 时，个体xj必须被评估。所以进一步在PFj上增加了拉伸操作，如式(13)所示：

即将个体的第一层适应值评估概率PFj的取值范围由[0.2，0.5]线性拉伸到[0.4，1]，增加前期适应值评估经验较弱个体的适应值评估概率。

2.1.2 第二层适应值评估概率

除了个体的历史经验信息以外，还需要考虑的就是个体当前的适应值。显然，当评估次数极其有限时，自然是希望将这有限的适应值评估次数用在更有可能寻找到问题最优解的个体上。适应值越好的个体，接近最优解的概率也相应越高。因此，在这里基于每个个体的适应值，为每个个体xj设计了第2 层的适应值评估概率PSj。具体的设计思路与AED-DDE 算法中的PLS 策略类似，按照个体的适应值对个体进行由坏到好的排序。接着，设置个体xj的第二层的适应值评估概率PSj如式(14)所示：

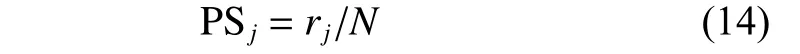
式中：rj表示第jth个个体在适应值排序中的位置。也就是说，适应值越好的个体就拥有更好的第二层的适应值评估概率PSj。

2.1.3 完整的概率评估机制流程

在我们的算法设计中，使用两个适应值评估概率的最大值作为个体最终的适应值评估概率Pj，如式(15)所示。

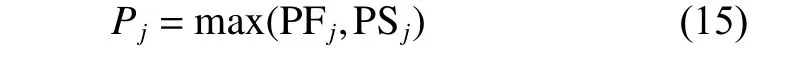
具体来说，如果个体xj的第1 层适应值评估概率PFj很小但是第2 层的适应值评估概率PSj很高，这说明个体xj具有很好的适应值，寻找到最优解的概率也会很高，此时，即使个体xj的第一层适应值评估概率PFj很小，依然为个体xj设置较大的适应值评估概率，加快算法找到问题最优解的速率。同样，如果个体xj的第一层适应值评估概率PFj很高但是第2 层的适应值评估概率PSj很小，这说明个体xj虽然适应值较差，但个体xj前期的适应值评估经验较弱，选择概率较为模糊，此时，为了提升算法的准确性，同样为个体xj设置较大的适应值评估概率，进一步丰富并优化个体xj的历史评估经验，方便后续算法性能的提升。这两个适应值评估概率的结合，可以进一步增强算法的优化性能。

在算法运行初期结束后，就开始采用概率评估机制。在这个阶段中，每个个体xj会根据自身的适应值评估概率Pj来选择性评估。如果该个体xj满足自身的适应值评估概率Pj，则对产生的试验向量ui进行适应值评估，通过比较ui与xj的适应值来判断是否对xj进行更新，并采用上述方法相应地更新个体xj的选择概率PUj和PXj以及第1 层的适应值评估概率PFj。

若是该个体xj并不满足自身的适应值评估概率Pj，则不对产生的试验向量ui进行适应值评估，而是根据前期积累的历史经验，直接根据选择概率PUj和PXj来判断是否对xj进行更新，即如果个体xj满足自身的选择概率PXj，则直接忽略试验向量ui，不对个体xj进行更新。如果个体xj满足自身的选择概率PUj，则直接用试验向量ui替换掉个体xj。然而，由于此时并没有对试验向量ui进行适应值评估，试验向量ui没有相应的适应值，在这种情况下，即使个体xj更新了，依然使用它之前的适应值作为更新后个体的新适应值。同时，由于并没有对个体的适应值进行评估，此时个体xj的选择概率PUj和PXj以及第一层的适应值评估概率PFj不进行更新。

综上，概率评估机制所节省下来的FEs 可以提供给那些更需要评估的个体，增加种群的迭代次数，提升算法的求解精度；同时，概率评估机制充分捕捉了算法运行过程中每个个体的历史经验信息，实现了信息的充分利用，有利于算法的进一步搜索；最后，双层概率的结合使用互为补充，从多方面决定个体的适应值评估概率，丰富了算法的设计，进一步提升了算法的优化性能。完整的概率评估机制PE 的算法伪代码如算法3 所示。

算法3PE 算法

2.2 完整的PEDE 算法

结合AED-DDE 算法与以上的概率评估机制PE，完整的PEDE 算法伪代码如算法4 所示。

算法4PEDE 算法

1)结合了AED-DDE 算法中基于AED 的小生境策略以及基于PLS 的局部搜索策略，可以避免种群划分的困难以及小生境参数的敏感度，同时使得算法可以更加精确地找到所有的全局最优解。

2)概率评估机制的提出为算法节省FEs，便于算法将及其有限的FEs 提供给那些更需要评估的个体，同时增加种群的迭代次数，提升算法的求解精度。

3 数值实验分析

3.1 实验设置

采用目前最主流的多峰值优化测试集IEEE CEC 2013[33]来测试PEDE 的算法性能。

多峰值优化问题有两个重要的评估指标，分别是最优解寻找率(peak ratio，PR)和成功运行率(success rate，SR)。对于一个给定的最大适应值评估次数MaxFEs 和一个准确度ε，PR 指的是算法多次运行中，全局最优解的平均找寻率；SR 指的是算法的成功运行比率，其中一次成功运行表示算法可以在当次运行中找到该问题的所有全局最优解。

PEDE 的种群规模N的设置如表1 所示，而MaxFEs 的设置则是引用IEEE CEC 2013 多峰值优化测试集的要求。此外，PEDE 中使用的变异策略为 DE/rand/1，放大系数F与交叉概率CR 分别设置为0.9 和0.1。所有的算法独立运行51 次，对比实验结果的均值。此外，采用准确度ε=10−4来测试算法性能，该准确度的使用最为普遍[15-28]。

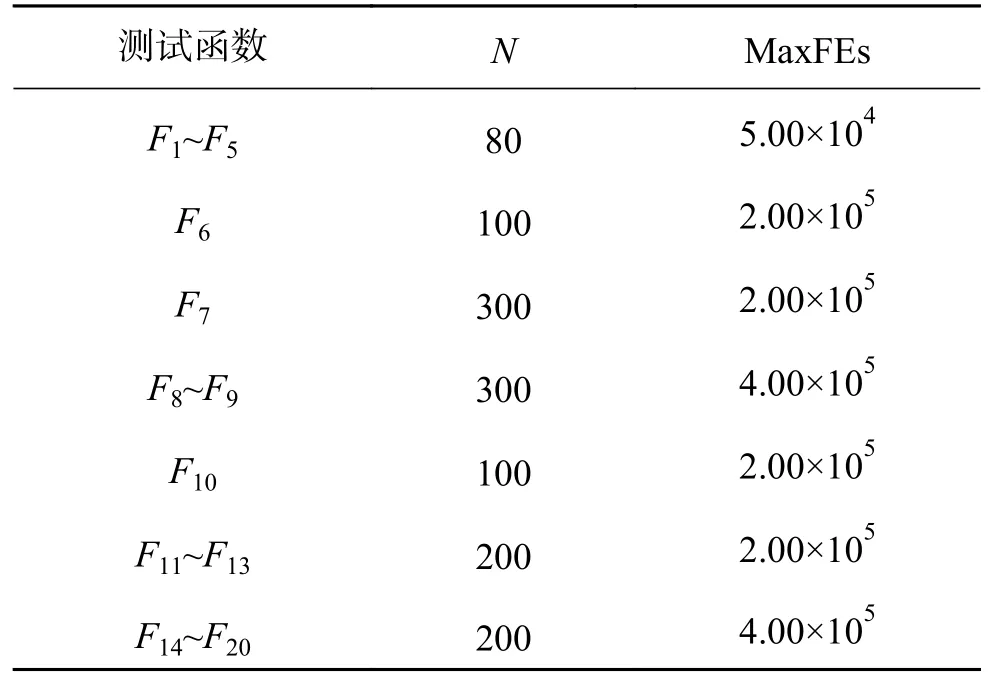
表1 参数设置Table1 Parameters setting

比较PEDE 与以下15个多峰值优化算法，它们分别是小生境策略算法CDE[15]、SDE[16]、NCDE[18]、NSDE[18]、Self-CCDE[17]、Self-CSDE[17]、AED-DDE[29]；新变异策略算法LoICDE[25]、LoISDE[25]、R3PSO[34]、LIPS[35]， PNPCDE[26]、LMCEDA[31]、LMSEDA[31]；以及多目标优化算法MOMMOP[32]。这些算法都是近年来的多峰值优化中的代表性主流成果，时间跨度从2004 年到2021 年。所有的算法采用相同的MaxFEs 设置，以此来保证比较的公平性。

3.2 实验结果

3.2.1 与主流多峰值优化算法实验结果对比

表2 列举了PEDE 与其他多峰值优化算法在准确度ε=10−4下PR 与SR 的实验结果。为了突出显示，最好的PR 结果加粗显示。此外，Wilcoxon 秩和检验在α=0.05 下用来做不同算法之间PR 结果的显著性分析[36]。符号“+”、“−”和“≈”分别表示算法PEDE 要显著好于(+)、显著差于(−)以及无明显差异(≈)对比算法。从表2 中可以看到，在函数F1～F6和F10～F12上，只有PEDE 和AED-DDE 可以在每一次运行中都找到所有的全局最优解，PR 值与SR 值均为1.000，而其他的任何一个算法都不能达到相同的效果。在函数F7～F9上，Self-CCDE 和MOMMOP 取得了令人非常满意的结果，甚至结果要好于PEDE，特别是MOMMOP，PR 值与SR 值均为1.000。然而，PEDE 在函数F7～F9上也取得了很好的结果，要显著好于其他的多峰值优化算法。同时，Self-CCDE 和MOMMOP 在函数F11和F12上的结果要显著差于PEDE。在函数F13上，PEDE 取得了与LIPS 近似的实验结果，但要显著好于其他所有的多峰值优化算法。同时，LIPS 在其他函数上的结果都不能优于PEDE。在函数F14～F20上，PEDE 在函数F14、F16和F20上都取得了最好的实验结果。需要注意的是，F20是IEEE CEC 2013 中最复杂、维度最高的测试函数，许多算法在F20上甚至不能找到任何一个全局最优解。即使PEDE 在函数F15、F17和F19上的实验结果要略微逊色于LMCEDA 和LMSEDA，PEDE 的实验结果依然要显著好于其他的多峰值优化算法。同时，与算法LMCEDA和LMSEDA 相比，PEDE 在其他函数上的效果要明显好于LMCEDA 和LMSEDA，尤其是在4个拥有着数量巨大的全局最优解的函数F6～F9上。

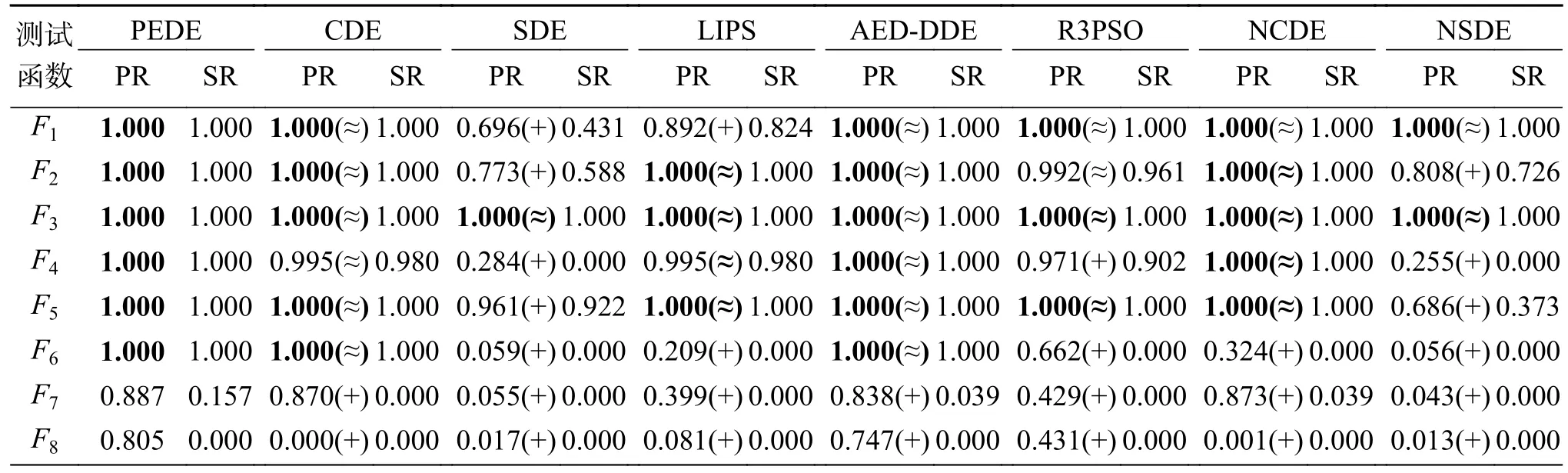
表2 IEEE CEC 2013 测试集在准确度ε=10−4 下的PR 与SR 的实验结果Table2 Experimental results of IEEE CEC 2013 in PR and SR at accuracy levelε=10−4

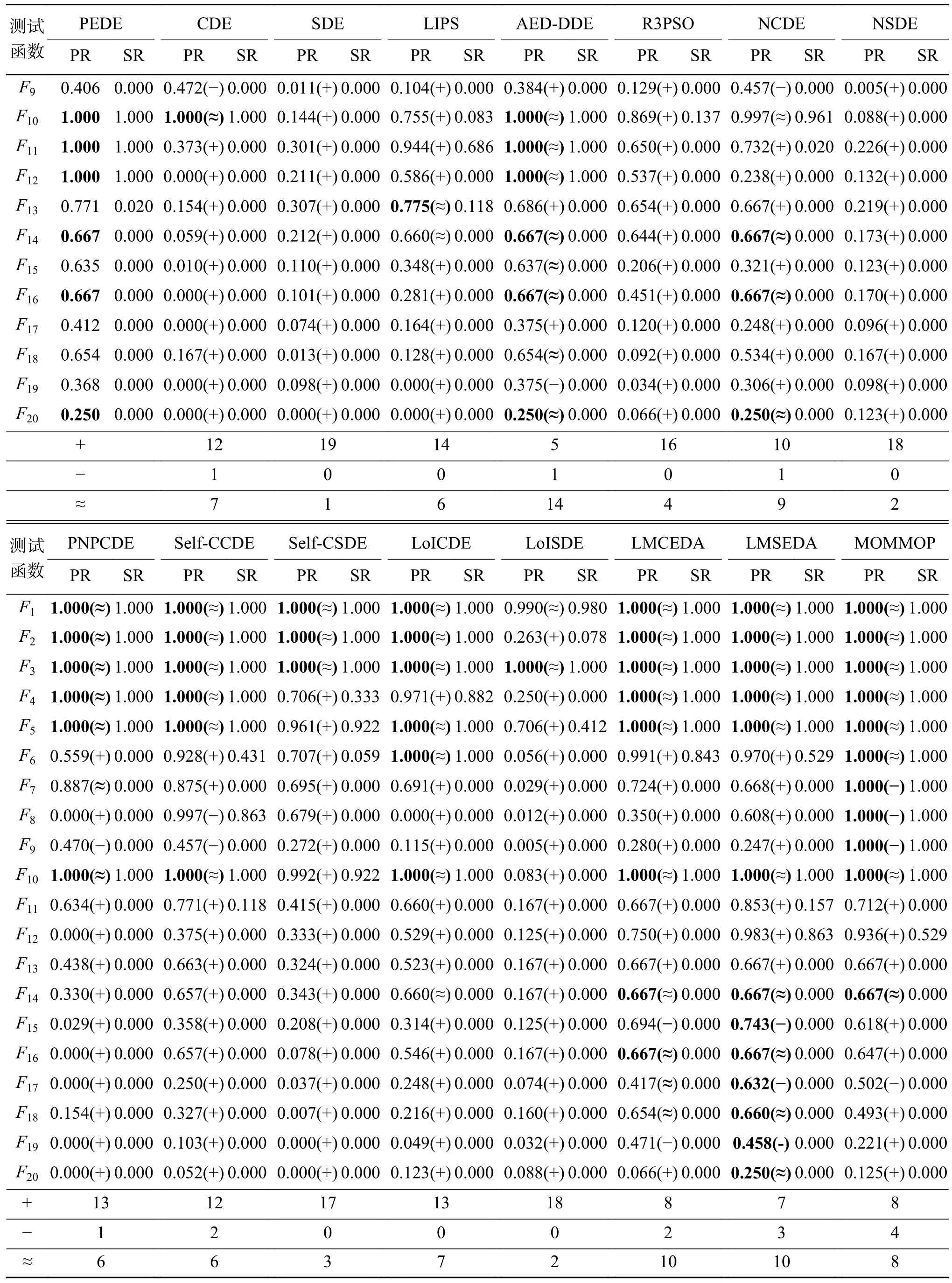
续表2

总之，PEDE 分别要在12、19、14、5、16、10、18、13、12、17、13、18、8、7 和8个函数上好于CDE、SDE、LIPS、AED-DDE、R3PSO、NCDE、NSDE、PNPCDE、Self-CCDE、Self-CSDE、LoICDE、LoISDE、LMCEDA、LMSEDA 和MOMMOP。相反，PEDE 只在1、1、1、2、2、3 和4个函数上要略微差于CDE、NCDE、PNPCDE、Self-CCDE、LMCEDA、LMSEDA 和MOMMOP。同时，PEDE 的效果要好于AED-DDE，说明了概率适应值评估机制的有效性。

为了有一个更加直观的视角来看PEDE 算法的求解效果，在8个可视化函数上将PEDE 算法最终的种群分布展示出来。

如图1 所示。

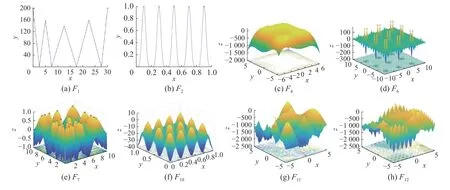
图1 8个测试函数上 PEDE 的最终种群分布Fig.1 Final population distribution of PEDE on 8 selected functions

正如我们从图1 中看到的，PEDE 可以找到问题所有的全局最优解。即使当问题有数量巨大的全局最优解时，如图1(d) 和图1(e)，在函数F6和F7上，PEDE 依然可以找到所有的全局最优解。当求解一些包含有数量巨大的局部最优解的复杂问题时，如图1(g) 和图1(h)，在函数F11和F12上，PEDE 可以维持种群多样性和探索能力，有效地避开局部最优解，将所有的全局最优解找到。

3.2.2 与多峰值测试集冠军算法实验对比

为了进一步说明PEDE 算法的优越性，在本节中，比较PEDE 与多峰值优化测试集 IEEE CEC 2013 的冠军算法(niching migratory multi-swarm optimizer,NMMSO[37])。为了公平比较，直接引用NMMSO 算法在多峰值优化测试集IEEE CEC 2015 上的实验数据。

PEDE 与NMMSO 在准确度ε=10−4下的PR 与SR 的详细对比结果如表3 所示，其中最好的PR 实验结果加粗显示。

从表3 中可以看到，PEDE 在7个函数上的实验结果要优于NMMSO，而在7个函数上的实验结果要略差于NMMSO。然而，可以看到，PEDE可以在9个函数上每一次运行中都找到问题所有的全局最优解（函数F1～F6和F10～F12），PR 值与SR 值均为1.000，而NMMSO 仅可以在7个函数上找到问题所有的全局最优解（函数F1～F5、F7和F10）。同时，在PEDE 差于NMMSO 的测试函数上，PEDE 也实现了与NMMSO 近似的实验结果。例如，在函数F14、F17和F19上，NMMSO 的PR 实验结果分别是0.720、0.468 和0.450，而PEDE 也实现了近似的PR 实验结果，分别是0.667、0.412 和0.368。此外，在高维复合函数F16～F20上，PEDE 在3个函数上要好于NMMSO，而NMMSO 仅在2个函数上要好于PEDE。特别地，在函数F20上，也是多峰值优化测试集IEEE CEC 2013 中最复杂的函数，PEDE 的实验结果要好于NMMSO。

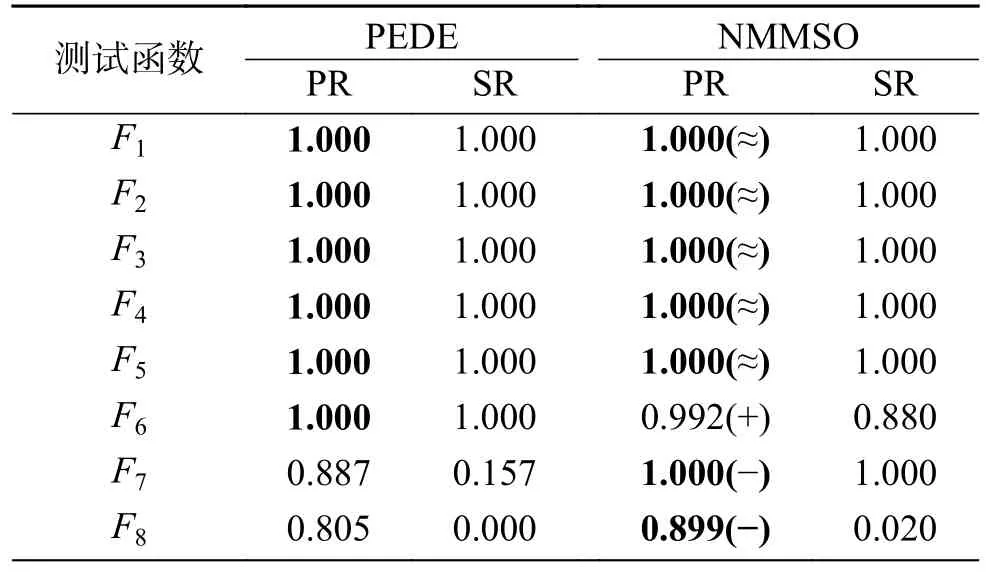
表3 PEDE 与NMMSO在准确度ε=10−4 下 的PR 与SR 的实验结果对比Table3 Experimental results between PEDE and NMMSO in PR and SR at accuracy levelε=10−4

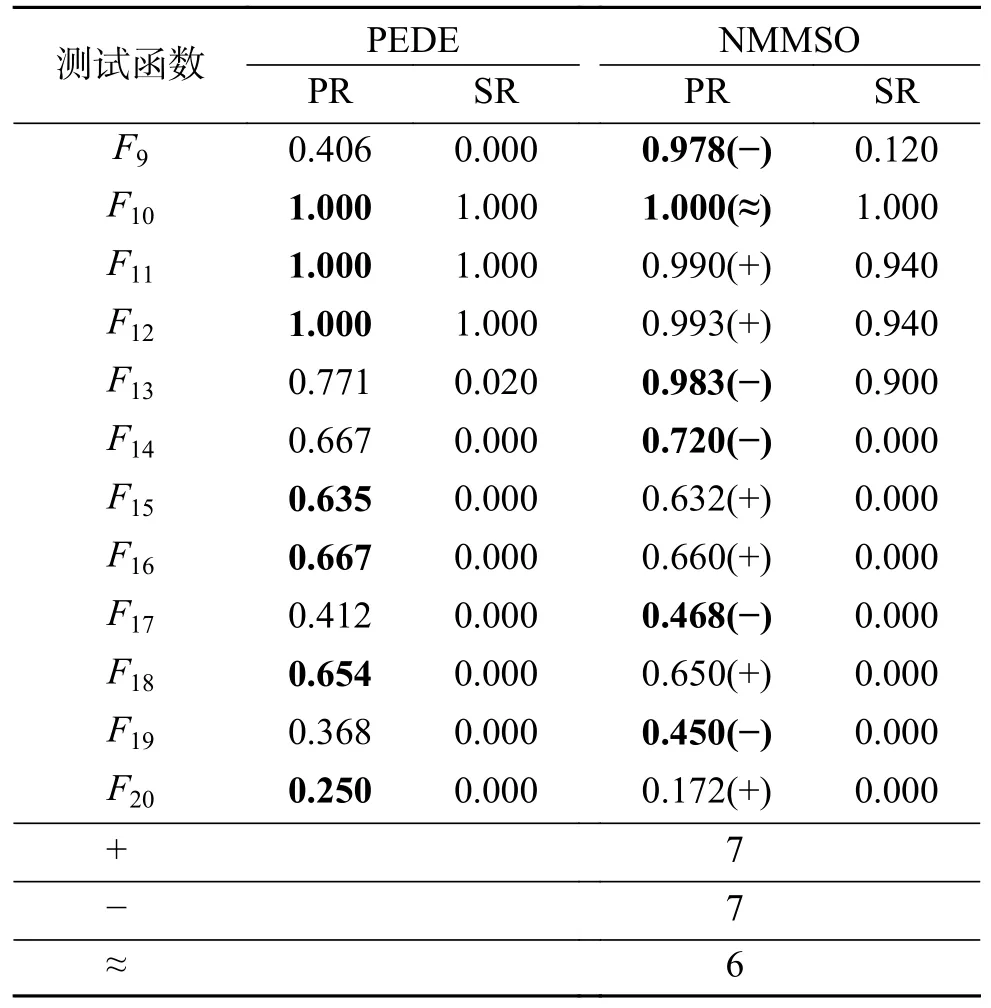
续表3

总之，PEDE 可以实现近似甚至好于多峰值优化测试集IEEE CEC 2013 的冠军算法的实验结果，特别是在一些复杂度较高的函数上。

3.2.3 概率评估机制性能测试

从表2 中可以看到，PEDE 的效果要好于AED-DDE，说明了概率适应值评估机制的有效性。在本节中，进一步测试概率评估机制的性能。将概率评估机制应用在其他的多峰值优化算法中来测试其性能。由于我们的概率评估机制适用于DE 算法，因此在这里，将概率评估机制应用在N C D E[18]、LoICDE[25]、Self-CCDE[17]、PNPCDE[26]这4个基于DE 的多峰值优化算法中。这4个算法结合概率评估机制的算法变种命名为算法-PE，例如，NCDE 算法结合概率评估机制的算法变种命名为NCDE-PE。这4个算法与它们相应的算法变种在准确度ε=10−4下的PR 与SR 的详细对比结果如表4 所示。

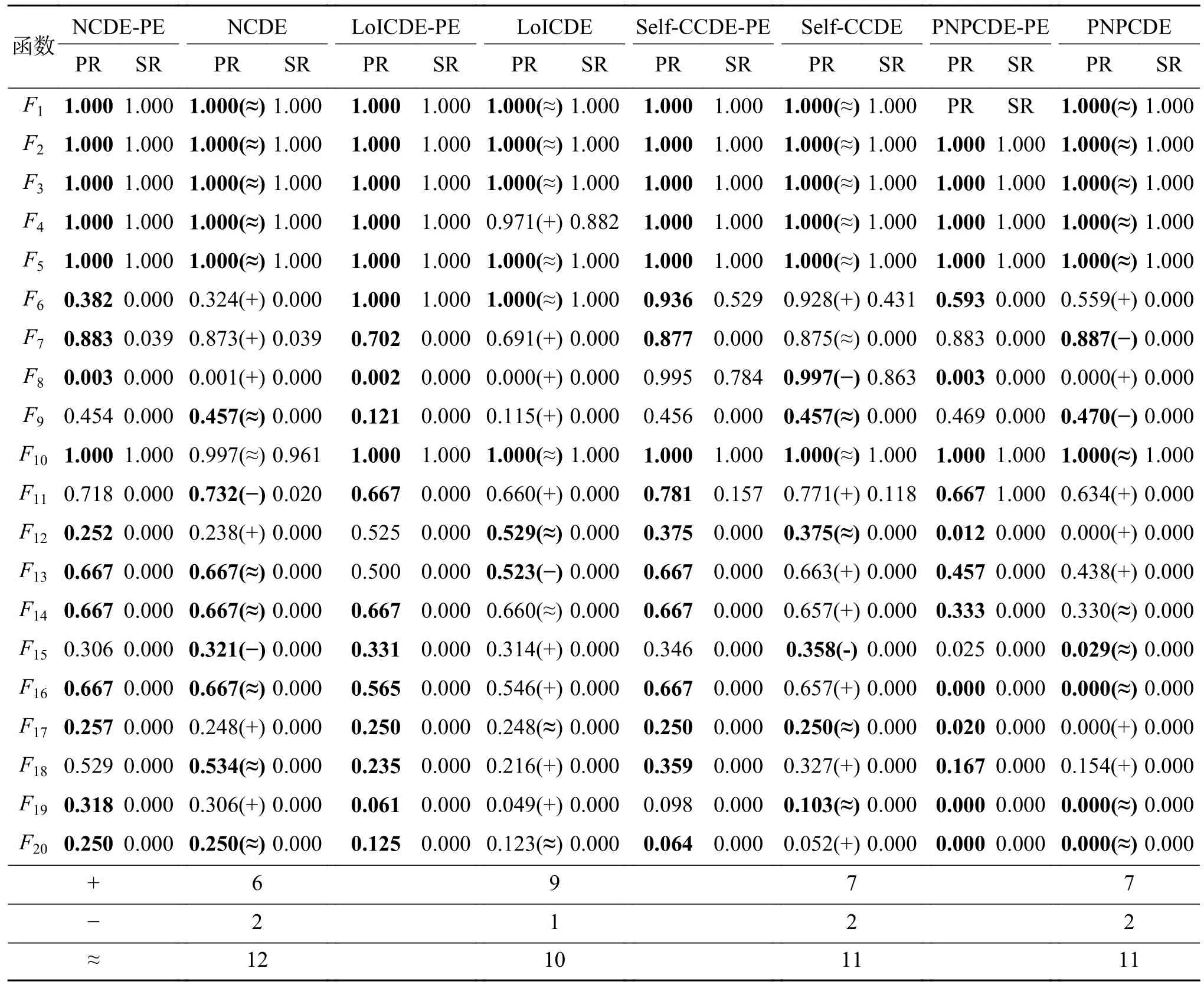
表4 多峰值优化算法及其在概率评估机制下的变种算法在准确度ε=10−4 下的PR 与SR 的实验结果Table4 Experimental results of multimodal optimization algorithms and their variants with PE in PR and SR at accuracy levelε=10−4

从表4 中可以看到，概率评估机制都可以在一定程度上提升这4个算法的性能，分别在6、9、7、7个函数上提升了NCDE、LoICDE、Self-CCDE、PNPCDE 的算法性能，尤其是在函数F6、F11～F14、F16～F20上，这4个结合概率评估机制的算法变种要显著好于原算法，进一步说明了概率评估机制的有效性与可拓展性。

4 结束语

本文基于之前的自适应分布估计的差分进化算法这一研究工作，进一步提出了一种概率评估机制。概率评估机制技术的提出，充分挖掘了个体在搜索和学习过程中的历史经验信息，对个体进行选择性评估，节省算法的适应值评估次数，增加算法迭代次数，从而提升算法的求解精度。而对个体历史经验的充分学习也进一步促进了种群在搜索空间中的充分探索。

将自适应分布估计的差分进化算法与概率评估机制有机结合，充分利用了二者的优势，形成了本文中提出的新算法PEDE。PEDE 不仅在多峰值优化测试集上取得了非常好的效果，同时，还将概率评估机制应用到其他的差分进化算法中，效果都有了一定的提升，也说明了概率评估机制的有效性与可拓展性。

在未来工作中，我们希望进一步增强PEDE算法在复杂多峰值优化问题上的求解性能，并将PEDE 算法应用在多峰值实际优化问题当中。