结合地标点与自编码的快速多视图聚类网络
马睿,周治平
(江南大学 物联网技术应用教育部工程研究中心,江苏 无锡 214122)
聚类作为一种无监督的学习方法可将给定的数据集根据数据的内在联系划分成多个集内相似度高而集间相似度低的子集,获得了数据挖掘、模式识别、图像分割等诸多领域的关注[1]。并且由于现实世界中多视图数据的普遍存在,例如,文档可以由不同语言来编写,基因可由不同技术来测量[2]。充分利用多视图数据以探索到更丰富、全面的数据特征从而获得更好的性能也成为聚类发展的方向。
多视图子空间聚类由于其优越的性能和丰富的可扩展性得到了飞速发展[3]。例如,Cao 等[4]在各个视图之间利用希尔伯特施密特独立性准则(HSIC)进行视图间相互约束,从而捕获到更丰富的数据关系。Wang 等[5]通过新颖的位置感知准则来利用多个视图的互补信息,同时通过一致性约束来获得多个视图的通用聚类指示矩阵。Brbic等[6]在生成多个视图的联合亲和度矩阵时利用低秩稀疏进行约束,并将方法扩展到核空间以适用于非线性数据。Nie 等[7]通过避免引入超参数的完全自动加权方案来为每个视图分配不同的权重以区分不同视图的重要性。Wang 等[8]试图通过整合编码的补充信息,利用具有最大依赖性的空间学习技术来形成多视图的信息丰富的完整感知相似性。Li 等[9]通过将潜在表示强制构造为最大程度接近多个视图的形式从而能够灵活地编码来自不同视图的互补信息。随着科技迅速发展,网络数据量也随之剧烈膨胀并越发呈现纷繁复杂状态。例如,Facebook 每月约报告60 亿张新照片,YouTube 每分钟约上传72 小时的视频。而聚类分析的主要任务之一就是对大规模数据集进行无监督分类[10]。虽然上述多视图聚类方法相较于单视图聚类方法在聚类精度方面有了质的提升,但是它们都呈现出较高的计算复杂度,从而在大规模数据集上的使用具有局限性[11]。
为了提升面向大规模数据集的可扩展性,亟需找到一种优质的能降低计算复杂度的聚类算法,为了解决这一问题,He 等[12]利用随机傅里叶特征来显式表示内核空间中的数据,显式特征映射可显著加快特征向量近似,从而提高谱聚类预测速度。Tian 等[13]发现自编码器和谱聚类本质上都是在保留原始数据最重要数据特征的同时实现降维处理,因此运用自编码器来替代谱聚类中的拉普拉斯矩阵特征分解,对于大规模数据集来说,这一处理极大地减少了内存消耗,但此方法仍需要直接处理规模庞大的数据。因此Yin 等[14]提出了一种具有局部相似性表示的基于地标的光谱聚类方法,该方法首先通过使用给定的相似度函数对原始数据点的“最相似”地标进行编码,然后对编码数据点进行奇异值分解以得到频谱嵌入数据点,再利用传统聚类方法例如K-means 对嵌入数据点进行划分。Banijamali 等[15]将地标表示与非线性低维映射相结合,同时避免了直接处理大规模数据集与拉普拉斯矩阵特征分解步骤,实现了更精确的快速聚类方法。虽然上述基于谱聚类的扩展算法十分有效地降低了谱聚类的计算量,但它们都是针对单视图谱聚类进行的,对于多视图学习场景显然无能为力。
综上所述,本文提出一种结合地标点和自编码的快速多视图聚类方法。为了提取大规模数据集中的强代表性点以降低存储开销,首先利用加权PageRank 排序算法在每个视图中选取原始数据中权重较高的数据点作为每个视图的地标点,为了避免传统的手工生成相似度矩阵中指数函数与近邻点个数的选择,本文利用凸二次规划函数直接从数据中获得每个视图的相似度矩阵,融合多视图信息,将生成的多视图共识相似度矩阵作为自编码器的输入,利用自编码器替代拉普拉斯矩阵特征分解获得多视图数据的联合嵌入表示,最后利用K-means 算法进行最后的聚类划分。为了避免微调环节覆盖之前所得最优参数从而获得更精确的聚类结果,本文将自编码器的重建损失和聚类损失放在同一学习框架下从而能够对自编码器的参数和聚类中心进行联合更新。
1 相关算法理论
1.1 多视图子空间聚类
鉴于融合多视图数据以捕获到更全面的聚类有效信息是十分有必要的,多视图子空间聚类最近获得了大量关注。给出多视图数据
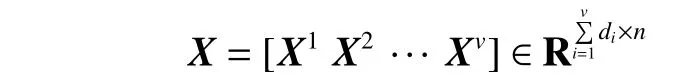
根据自表示思想通过一个稀疏系数矩阵重构原始数据,则多视图子空间聚类网络的目标函数为

式中:Si为第i个视图的相似度矩阵,不同形式的f(·)可以给出不同性质的解。例如,文献[4]利用HSIC 鼓励图对之间的差异性,文献[6]利用低秩稀疏对相似度矩阵Si进行约束,文献[9]生成了一个潜在的表示空间以灵活编码多视图信息。但是所有这些多视图子空间聚类方法每个视图的相似度矩阵Si的大小都为n×n,从而都至少需要O(n2k)的时间,且都涉及拉普拉斯矩阵特征分解,因此具有计算效率以及存储空间上的劣势,使其很难扩展到样本点n数量庞大的大规模数据集上。
1.2 锚图构造
相似度矩阵的构造对于谱聚类来说非常重要,对于构造大规模数据集的相似度矩阵,锚图是一种十分有效的方法[16]。
利用K-means 或随机选择等方法从含有n个样本点的数据集中提取出具有m(m≪n)个样本点的子集,每个子集中的点作为地标点来逼近原数据集,引入k近邻点来度量点对之间的局部亲和力。利用地标点与原数据来构造一个稀疏相似度矩阵Z∈Rn×m:
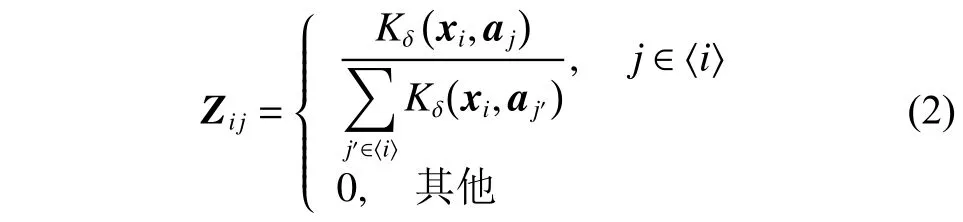
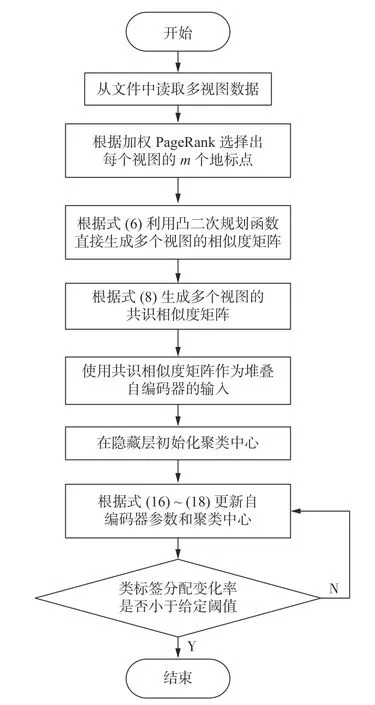
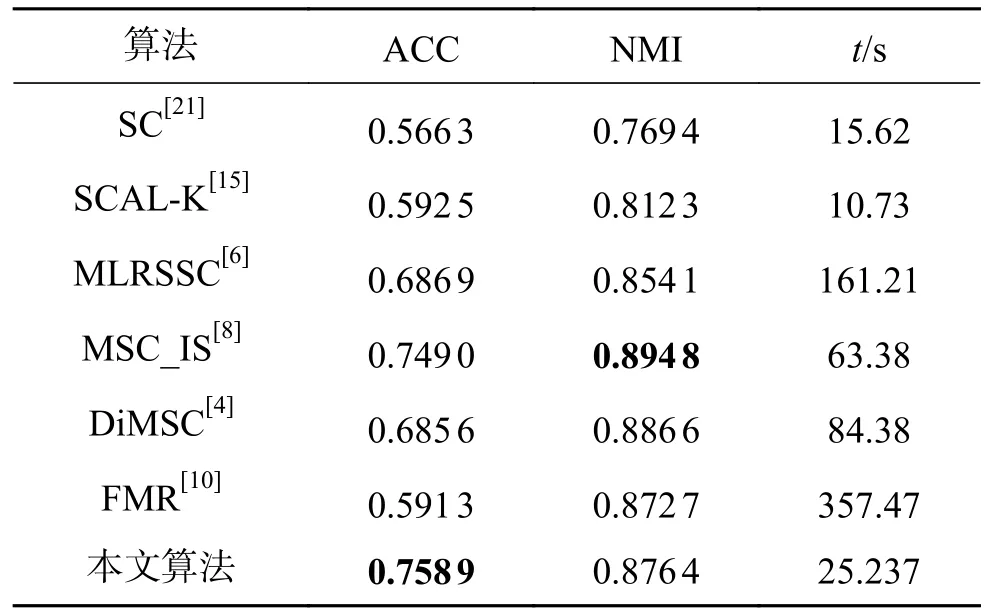
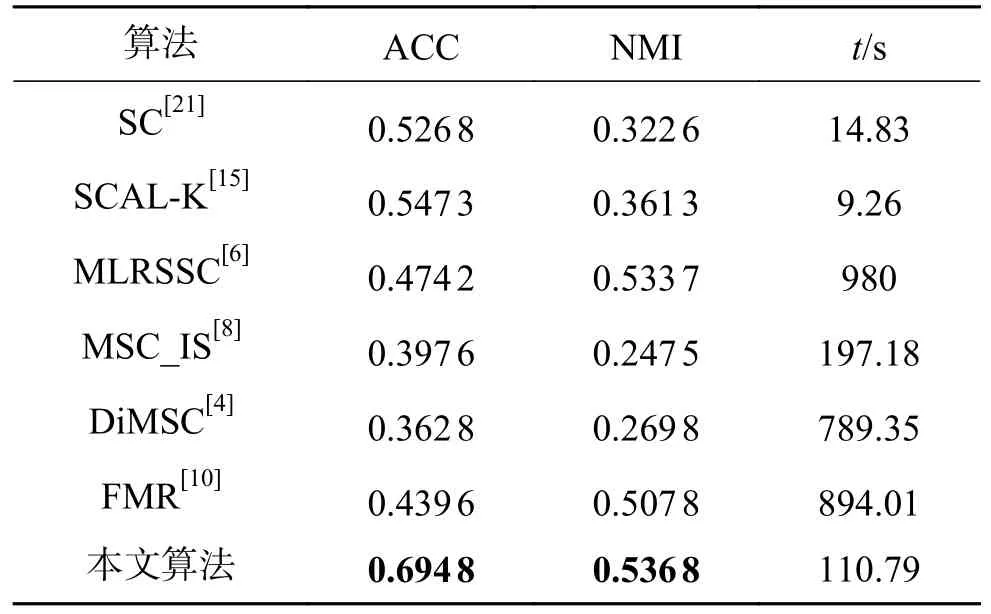
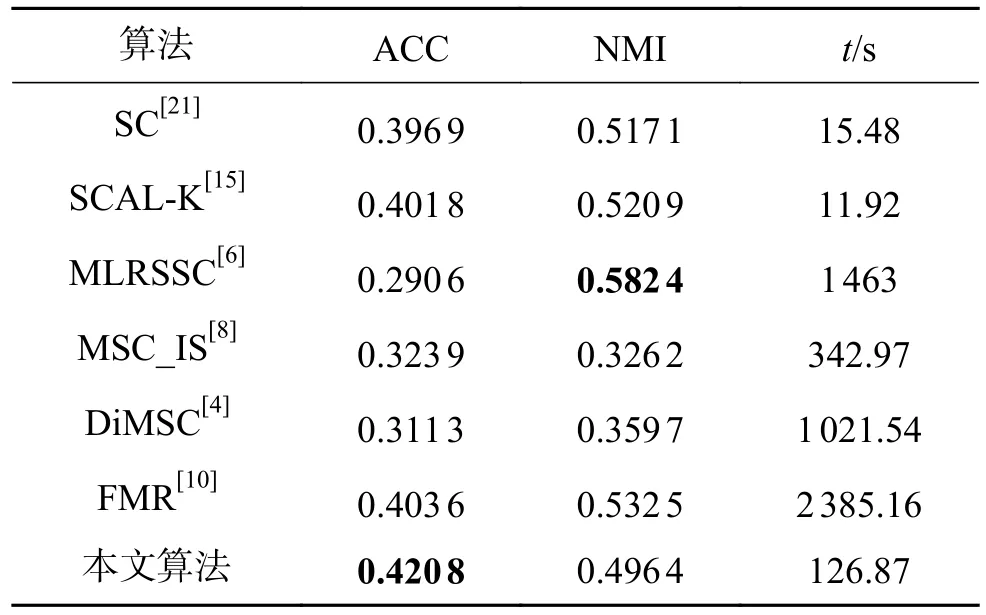
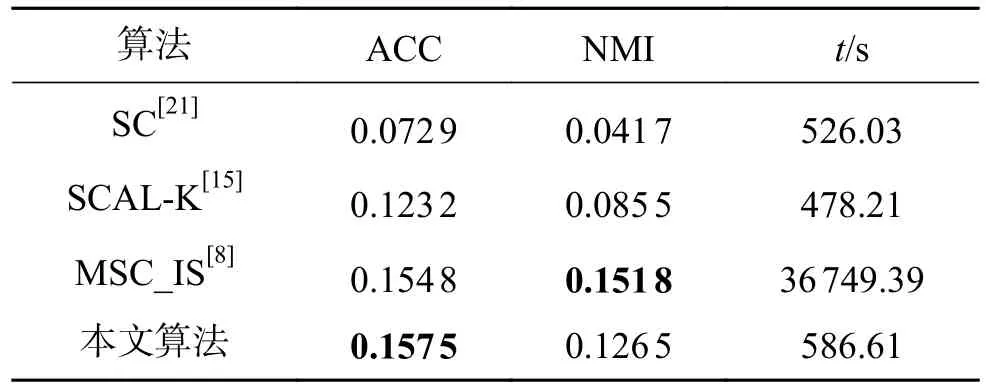
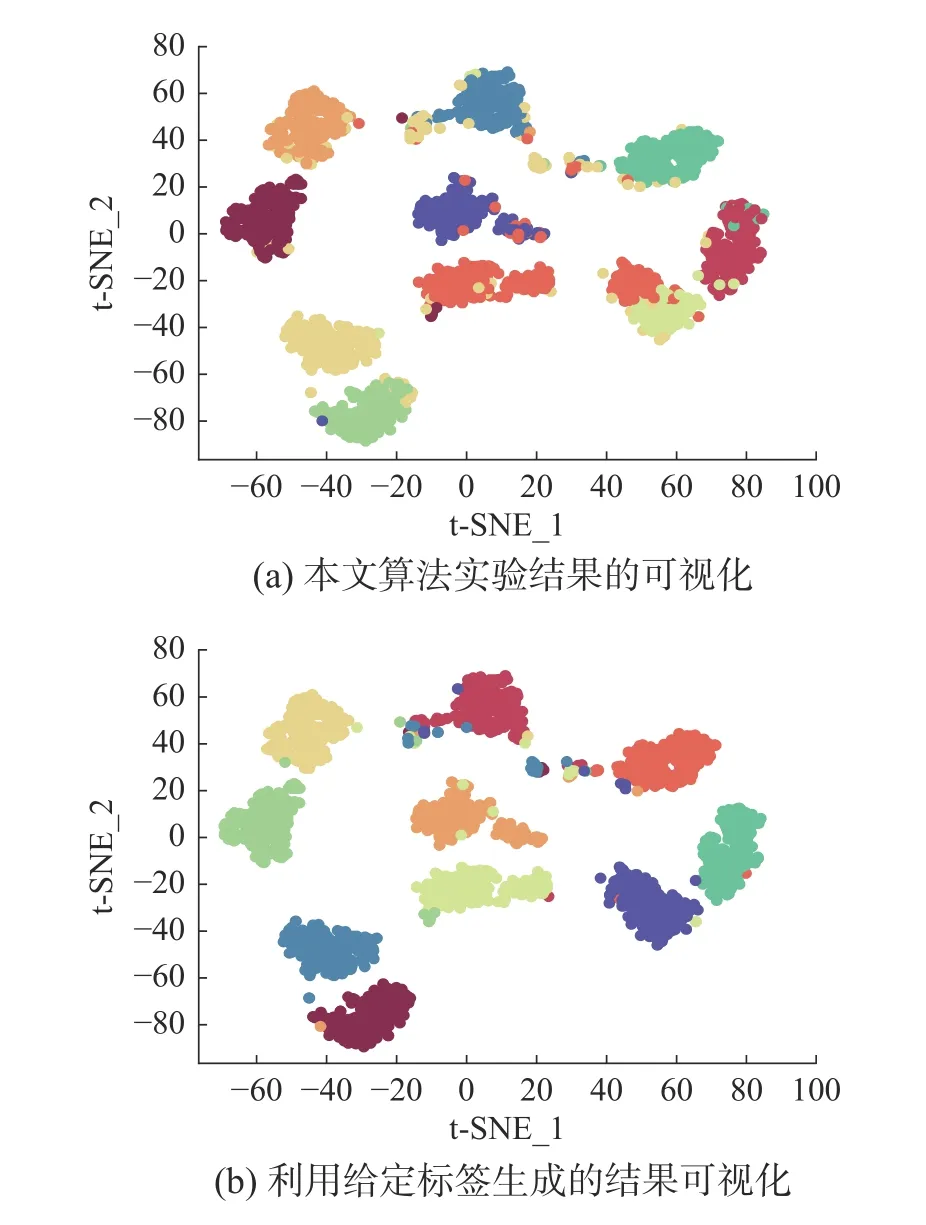
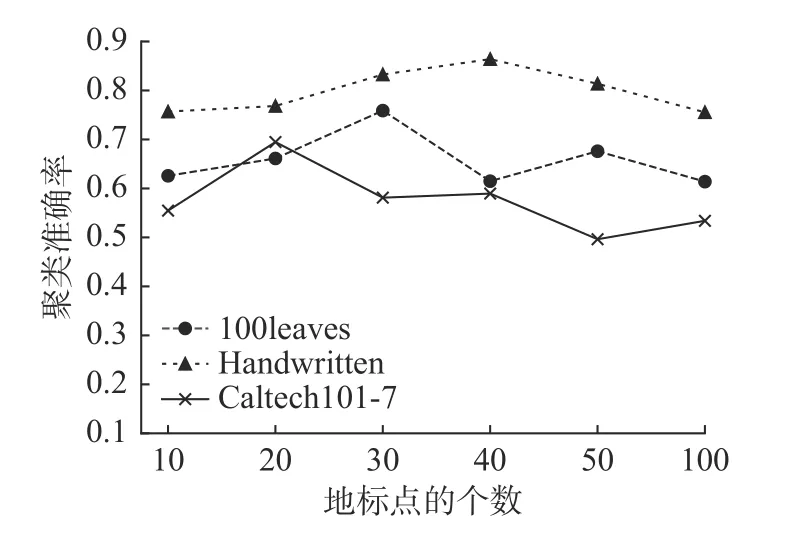
式中:〈i〉表示xi的r(r 然而此启发式策略存在一个总是被忽略的固有缺点,即所构建的图形质量很大程度依赖于指数函数和近邻点个数r的选择,因此,下游任务可能会受到负面影响。 大规模数据集中存在很多冗余数据,少量样本完全满足重建子空间的需求。传统的地标点选择方法有文献[15]中的随机抽样和使用K均值中心点作为地标点的方法。但是随机抽样可能导致地标点彼此过于靠近,这可能导致邻域重叠。而采用K均值中心作为地标点的方法运行时间过长且当数据规模极大,超出系统的内存时,K均值聚类算法需要不断地执行读取操作[17]。因此,本文采用文献[18]中的加权PageRank算法来为每个视图选择wpr值最高的m个样本点作为地标点。 为了避免式(2)形式生成相似度矩阵的不足之处,本文在多视图聚类框架下采取直接从数据生成相似度矩阵的方法,该方法不仅能揭示数据低维结构,还对噪声和数据规模有着极强的鲁棒性。在多视图思想下利用重构误差和约束项建立采用地标点的多视图聚类模型目标函数: 式中:V为从不同来源或者利用不同收集方式获取到的视图总个数;Xv、Av、Zv分别为第v个视图的原始数据矩阵、地标点矩阵、相似度矩阵。因为无需设置近邻点,该形式生成的相似度矩阵不再受困于只能捕获到数据的局部分布这一桎梏,并能完整感知数据从而保留数据的全局结构。可以看出,与式(2)相比,对于每个视图,本方法只需在mn个数据点之间计算相似度矩阵而非传统子空间聚类中的n2个数据点。对于大规模数据集来说,此举可在利用多视图一致性与互补性确保聚类精度的同时使复杂度显著降低。 由于现实世界中数据的固有结构呈现出普遍非线性状态[19],将式(3)扩展到核空间中进行。定义φ:RD→H为从原始输入空间到核希尔伯特空间 H 的映射,对于每个包含n个样本点的视图,其变换后形式为 由m个地标点构成的强代表性数据矩阵的变换后形式为 核函数定义为 则式(3)可转变为 通过求解式(4)可以捕获到φ(x)与φ(a)间的线性稀疏关系,即样本点x与地标点a间的非线性关系。将式(4)按列重新写出: 进而式(5)可转变成为二次型形式(6),从而能直接通过凸二次规划函数求解得到各个视图的由数据直接生成的相似度矩阵Zv: 自编码器是一种利用非线性变换函数fi将原始输入xi映射到低维嵌入空间,获得嵌入表示hi,再通过另一映射函数gw’对hi进行解码重构,通过最小化原始输入xi与嵌入表示hi的重构输出yi之间的重构损失Lr来迭代更新的人工神经网络[14],其均值误差测量形式目标函数为 文献[15]同样利用自编码器来配合聚类,然而其仅在聚类步骤前简单叠加无监督深度学习框架,这样形成的低维嵌入空间可能反而会损坏聚类分配效果。为此本文将聚类步骤和表示学习统一到一个基于KL 散度的利用损失函数迭代更新自编码器参数{M1、M2;θ1、θ2}和聚类中心cj的联合学习框架中,从而能联合优化聚类标签的分配和特征的学习,也使位于自编码器隐藏层的低维特征能够最大限度的保留原始数据的固有局部结构。将聚类损失目标函数定义为 式中:Q为由t-SNE 测量的软标签的分布;P为由Q导出的目标分布。KL 散度衡量了两种不同分布之间的差异性,若对其进行最小化则能使得目标分布P能够尽可能接近聚类输出分布Q。qij表示根据t-SNE 测量得到的嵌入表示hi与聚类中心cj的相似程度[14],其表达式如下: pij则是由qij确定的目标分布: 因此,总体的优化目标函数为 其中,λ(0<λ<1)为控制嵌入空间失真程度的平衡参数。则根据mini-batch 随机梯度算法反向传播逐层训练网络后计算出的聚类损失Lc关于嵌入表示hi和聚类中心cj的梯度计算公式为 给定m为小批量样本数,η为学习速率,编码器权重M1、译码器权重M2、聚类中心cj的更新公式分别为 当连续两次更新的类标签分配之间的变化率小于给定的阈值 δ时迭代停止。 结合地标点与自编码的快速多视图聚类网络算法流程如图1 所示。 图1 所提算法流程图Fig.1 Flow chart of the proposed algorithm 当有v个视图,每个视图有n个样本点,每个视图的地标点个数为m时 :1)利用加权PageRank算法为每个视图进行地标点选择,因此本文地标点选择步骤的时间复杂度为O(vtmn),t为生成每个样本点的wpr 的迭代次数;2)构造多个视图的相似度矩阵,DiMSC 和FMR 等多视图子空间聚类方法由于未进行1) 地标点选择,在2) 中DiMSC 和FMR 算法构造的每个视图的自表示矩阵图形大小均为n×n,二者的计算复杂度分别为O(Tvn3+vdn2)、O(T(L+1))(n3+kn2),其中L表示FMR 算法中涉及的梯度下降法的迭代次数,T为DiMSC、FMR 算法总迭代次数。当数据规模n很大时,L、T≪n,因此DiMSC 和FMR 算法步骤2)的计算复杂度均可视为O(n3),这远远高于本文算法的m×n(m≪n)图形的计算复杂度O(vnm3)。3) 聚类步骤,DiMSC 和FMR 算法的步骤3)采用常规谱聚类,涉及到n2图的拉普拉斯矩阵特征分解,需要消耗O(n3)的时间复杂度,且存储开销极大。而所提算法采用自编码器替代拉普拉斯矩阵特征分解步骤,自编码器参数和聚类中心联合更新,仅需O(nD2+ndk)的时间,其中D为自编码器隐藏层的最大单元数,d为自编码器中间层的维数,k为簇数,与此同时存储开销也被大大降低。因为通常k≪d≪D,所以本文所提算法的总体时间复杂度为O(vtpn+vnm3+nD2)。可以看出,本文提出的采用地标点的快速多视图聚类网络的总体时间复杂度为样本点数n的线性次方,而DiMSC 和FMR 聚类算法的总体时间复杂度为样本点数n的三次方。表1 给出了所提算法与多视图聚类算法DiMSC、FMR 的时间复杂度对比结果。与通常的多视图聚类算法相比本文算法的效率大大提升,且所需的存储开销显著降低,从而可更适用于大规模数据集。 表1 不同方法时间复杂度对比Table1 Complexity analysis of different methods 为了证明本文所提方法对大规模多视图数据的适用性,选取100leaves、Handwritten(HW)、Caltech101-7/20、NUS-WIDE-Object (NUS)五个大规模的多视图数据集进行实验,每个数据集样本点数都在1000 以上,表2 为5个大规模多视图数据集的详细介绍,其中V为多视图数据集的视图编号。本文算法实验是在python3.7 运行,计算机配置为Intel Core i5CPU 1.6 GHz、4 GB 内存,操作系统为macOS Catalina。 表2 数据集介绍Table2 Description of the datasets 将本文方法所得聚类结果与样本真实标签进行比较,利用聚类准确率(ACC)、标准化互信息(NMI)和运行时间(Time)来作为性能评估指标,ACC 和NMI 取值均在0~1,值越大说明聚类性能越佳,运行时间越短说明算法越具有普遍适用性,即越适用于大规模数据集。 为证明本文提出的算法的有效性,将其分别与单视图聚类算法和多视图聚类算法进行对比,对比单视图聚类算法分别为文献[21]中的传统单视图谱聚类算法SC 和文献[15]中的使用K均值进行地标点选择后利用嵌入表示替代拉普拉斯矩阵分解步骤的SCAL-K,同时与4个近期出现的性能优异的多视图聚类算法DiMSC[4]、MLRSSC[6]、MSC_IAS[8]、FMR[10]进行对比。 为保证算法对比的公平性,所有对比算法都遵从算法原论文的实验设置,并调试参数获得其最优值。文献[15]中的SCAL-K 算法及本文算法的自编码器部分的编码器维度设置为p-500-500-2000-10,解码器部分为编码器的镜像,最小批量样本数设置为256,初始学习速率 η设为 0.1,停止阈值设置为h=10−3,并把控制嵌入空间失真程度的平衡参数 λ设置为 0.1。对于两个单视图聚类算法,在数据集的每个视图上运行实验后取多个视图里的最佳结果展示。 各个算法在5个数据集上的实验结果如表3~7所示。实验结果ACC 和NMI 中的性能最优异项被加黑标出。 表3 不同算法在100leaves 数据集上的表现Table3 Performance of different algorithms on the 100leaves dataset 表4 不同算法在Handwritten 数据集上的表现Table4 Performance of different algorithms on the Handwritten dataset 表5 不同算法在Caltech101-7 数据集上的表现Table5 Performance of different algorithms on the Caltech101-7 dataset 本文算法主要针对多视图聚类算法运行效率进行研究,可以看出,本文所提算法在表3~6的4个大规模多视图数据集上的运行速度均快于多视图聚类算法MLRSSC、MSC_IS、DiMSC、FMR,在表7 的NUS 数据集上同样快于多视图聚类算法MSC_IS。并且可以看出,在越大型的数据集上本文所提算法在运行时间上的优越性愈加明显,甚至可以达到相较于传统多视图聚类算法快几个数量级的效果,例如在NUS 数据集上MSC_IS 算法需要36 749.39 s 运行时间而本算法仅需586.61 s。因为执行时间的波动主要受选取的地标点个数m的影响,而100leaves 数据集取得最佳聚类结果时采用的地标点个数在几个数据集中为最小值,因此所提算法在100leaves 数据集上的运行时间最短。并且,同时采用了地标点与深度嵌入的单视图聚类算法SCAL-K(best)在多个数据集上的速度也快于SC(best)。上述现象均说明了采用地标点和嵌入表示替代矩阵分解对提升聚类算法运行速度的有效性。此外,当面对例如NUS 等每个视图的样本点数n超过10000 的数据集时,多种多视图聚类算法例如MLRSSC、DiMSC、FMR 会由于超出存储空间而无法得到实验结果,因此表7 仅给出了SC(best)、SCAL-K(best)、MSC_IS 的对比实验结果,与之相反的是本文所提算法在5个多视图数据集上均能得到实验结果,这证明了本文所提算法需要相较于传统多视图聚类算法更低的存储开销与计算复杂度。上述现象均证明了本算法较传统多视图聚类算法对大规模数据集具有更强的适用性。 表6 不同算法在Caltech101-20 数据集上的表现Table6 Performance of different algorithms on the Caltech101-20 dataset 表7 不同算法在NUS 数据集上的表现Table7 Performance of different algorithms on the NUS dataset 本文所提算法的性能在ACC 方面始终具有明显的优越性,均取得了所有实验算法结果ACC中的最大值,分别在100leaves、HW、Caltech101-7、Caltech101-20、NUS 上超过了第二佳算法1.3%、1.27%、21.3%、4.0%、1.75%。而NMI 方面本文算法同样可实现与其他多视图聚类算法相当甚至更好的性能,这证明了本文算法的一致性与稳定性。可以得出,本文所提出的采用地标点的快速多视图聚类算法在大幅度提升聚类速度的同时仍能够保持较好的聚类精确度。 为了进一步研究改进,本文在Handwritten 数据集上使用t-SNE 进行了二维可视化对比研究。图2(a)为本文算法的聚类结果视图,图2(b)为对比的利用给定标签生成的可视化结果,其中t-SNE_1、t-SNE_2 代表分别采用经t-SNE 方法降维后的二维数据的第1 列和第2 列数据作为可视化呈现的x轴和y轴。可以看出,虽然仍有少部分数据点未进行正确的聚类划分,但总体上本文算法可以良好地反映聚类结构,从而进一步证明本文算法可以在提升大规模数据集算法效率的同时保持较好的聚类精确度。 图2 Handwritten 数据集实验结果t-SNE 可视化Fig.2 Visualization of experimental results on the Handwritten dataset with t-SNE 由于所提方法采用地标点进行原数据重建,地标点个数m越少所提算法的运行时间就越短,但算法的精度却不一定和地标点个数m呈线性关系。因此本文作了敏感分析实验,以100leaves、Handwritten、Caltech101-7 等3个数据集的ACC为例,调整地标点个数m,图3 给出了模型对地标点个数的敏感性。可以看出,地标点个数m太少时难以完整代表原数据所有特征,而当地标点个数m过多时会使其本身的代表性降低并引入额外的错误从而导致性能变差。 图3 地标点敏感实验结果Fig.3 Results of landmark sensitive experiments 本文提出了一种结合地标表示和自编码器的多视图快速聚类方法,在多视图的框架下利用了加权PageRank方法选择地标点以减少存储开销,通过所选择的地标点重构原始多视图数据直接得到多视图共识相似度矩阵,在降低了计算复杂度的同时充分利用了多个视图中具有互补性与一致性的聚类有效信息,利用自编码器替代拉普拉斯矩阵特征分解,联合更新自编码器参数以及聚类中心,以保证聚类精度。在5个多视图数据集上的实验证明本文所提算法拥有良好的性能。但是本文中多个视图的信息仅是通过简单的相加来融合而并未进行视图差异区分,在未来,致力于进一步研究如何在保证计算速度的情况下更好将多个视图的信息具有区分性地融合,以更好地提升聚类性能。2 结合地标点与自编码的快速多视图聚类算法
2.1 图形构造
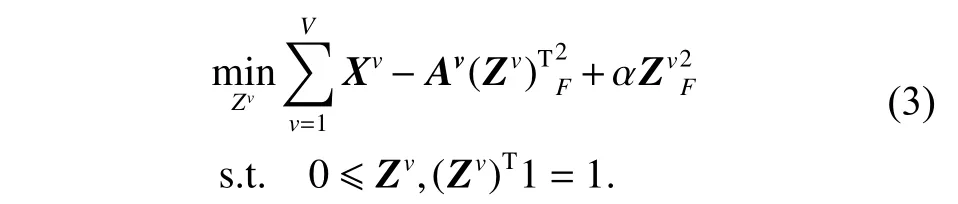


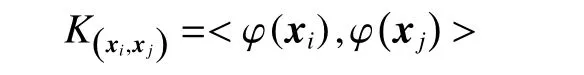
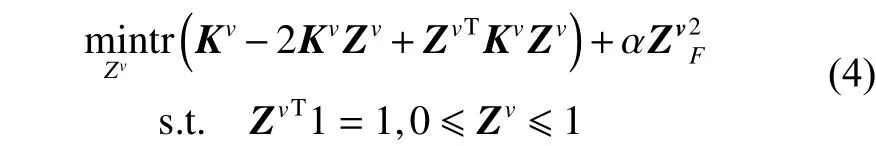
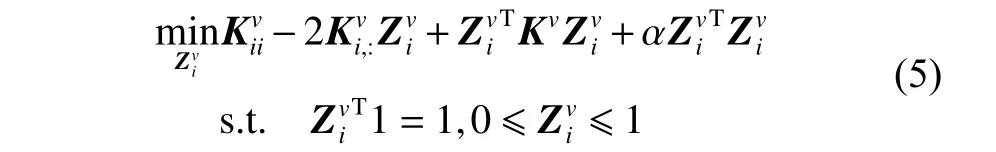

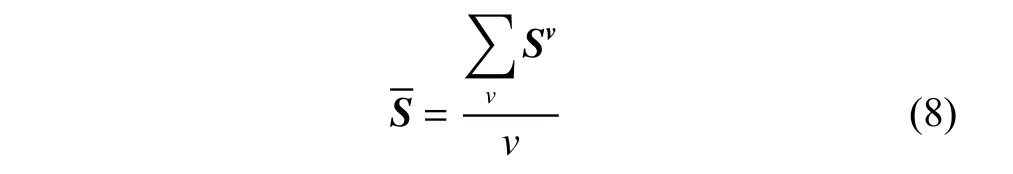
2.2 联合优化框架
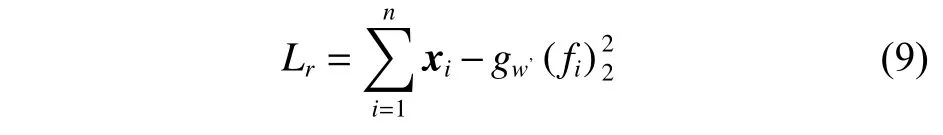





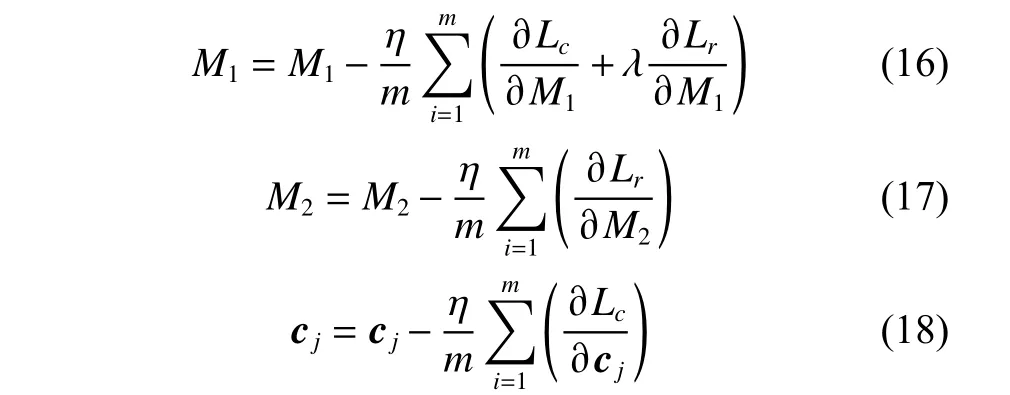
2.3 算法流程图
2.4 算法复杂度分析

3 实验与结果分析
3.1 实验环境及评价指标
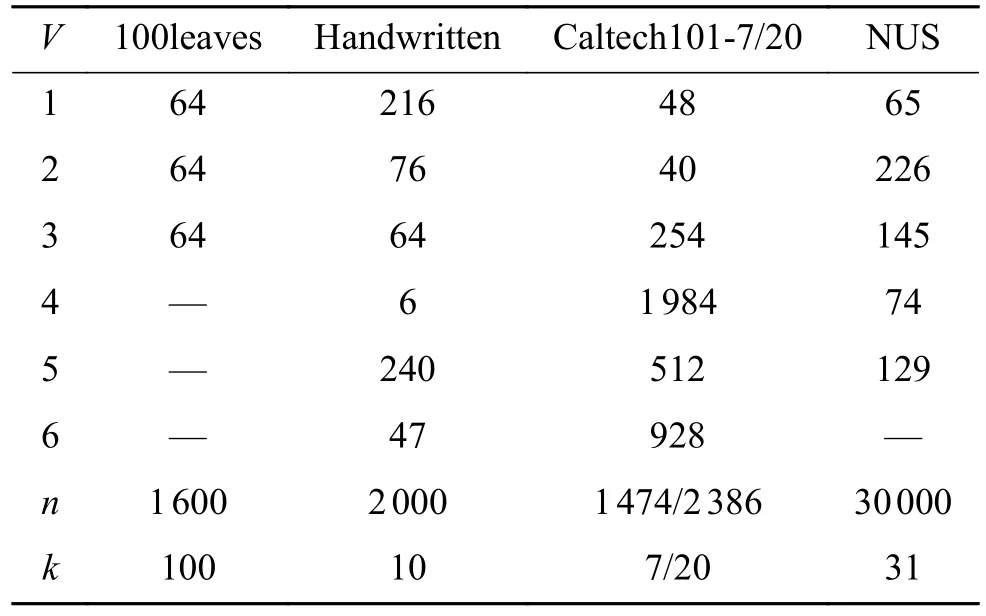
3.2 数据集及对比算法
3.3 实验结果分析

4 结束语
——编码器

