基于融合策略粒子群优化BP神经网络的磨煤机出粉量优化

李浩然,李 力,陆金桂

(南京工业大学 机械与动力工程学院,江苏 南京 211800)

磨煤机系统[1]作为锅炉重要的辅助设备,其出粉量直接影响着锅炉的整体性能,但是由于磨煤机出粉量受诸多耦合因素的影响,在实际生产中很难直接测量,通常采取一些间接方法进行测量。在间接测量中,目前采用的差压法[2]、功率法[3]等都是依靠单一变量判断磨煤机出粉量,这种方法存在一定的缺陷。近几年来,随着测量技术的不断发展和完善,基于多变量的软测量[4]方法被逐渐应用。韩洪兆[5]以证据理论对钢球磨煤机料位进行了软测量的研究,采用支持向量机建立证据合成(D-S)融合法则软测量模型，对磨煤机进行优化。赵凯[6]基于神经网络模型对磨煤机的一次风量进行了软测量。付国仙等[7]采用反向建模法基于神经网络建立磨煤机料位软测量模型,对料位进行了研究和优化。但是只优化单一变量对改进出粉量的效果有限,本文通过研究进出口压差、进口一次风量、进口一次风压、进口一次风温、出口风粉压力、出口风粉温度及电流等多个参数与出粉量的关系,综合优化多个参数,最大限度提高出粉量,提高锅炉整体性能。

误差反向传播算法(BP)神经网络作为软测量方法中数据驱动建模方法中的一种,具有建模过程简单方便、可操作性强等特点,是目前软测量建模研究的热点[8-9]。为了提高测量精度,通常采用融合策略优化模型。黄珍等[10]以混沌粒子群融合果蝇算法改进BP神经网络对磨矿粒度进行软测量。亢菲菲[11]以变步长最小均方算法(LMS)和改进相似极值的集合经验模态(EEMD)分解信号特征提取的方法对BP神经网络进行优化,进而对粉尘浓度进行软测量。白建云等[12]以BP神经网络建模对锅炉生成的NOx质量和浓度进行了软测量。由于研究的对象是磨煤机多个系统参数和出粉量之间复杂的非线性关系,而由于权阈值的选取问题,BP神经网络易陷入局部最优值,导致迭代效果较差、精度较低,影响优化效果。本文提出基于融合策略粒子群优化BP神经网络[13],以小生境法[14]改进粒子群种群多样性,有效增加粒子群算法多样性,并提高寻优速度;加入非线性变化的惯性权重,将学习因子与惯性权重相结合，并引入与惯性权重相关的时间因子,在提高粒子群算法统一性的同时，以惯性权重、学习因子来调整全局和局部搜索的平衡,达到提高精度和效率的双重目的。

将融合策略粒子群算法与BP神经网络结合,发挥融合策略粒子群算法的寻优能力,在权阈值空间搜索最佳权阈值,弥补BP神经网络软测量模型的权值和阈值选择不佳的缺陷,改善BP神经网络的非线性拟合能力,提高算法的速度和精度。利用该算法对磨煤机参数和出粉量建立软测量模型,并与实际测量结果进行对比,最后对磨煤机参数进行优化。

1 融合策略粒子群优化BP神经网络软测量模型

1.1 基本思路

基于BP神经网络的软测量原理就是通过实验点对输入和输出样本之间的非线性映射关系不断地拟合和学习,最终获得可靠的软测量模型。本文的软测量模型采用反向传播的BP神经网络,神经网络的识别信息是按正向传播的；但是其误差信息是按反向传播的,通过这种方式训练软测量模型,当输出的出粉量与真实出粉量有较大的误差时,神经网络模型就会将误差信息由输出层传递到隐含层,由隐含层传递到输入层逆向传播,之后采用误差最速下降法修正各层之间权阈值,直至输出数据的误差小于设定的误差。图1为软测量的神经网络结构。

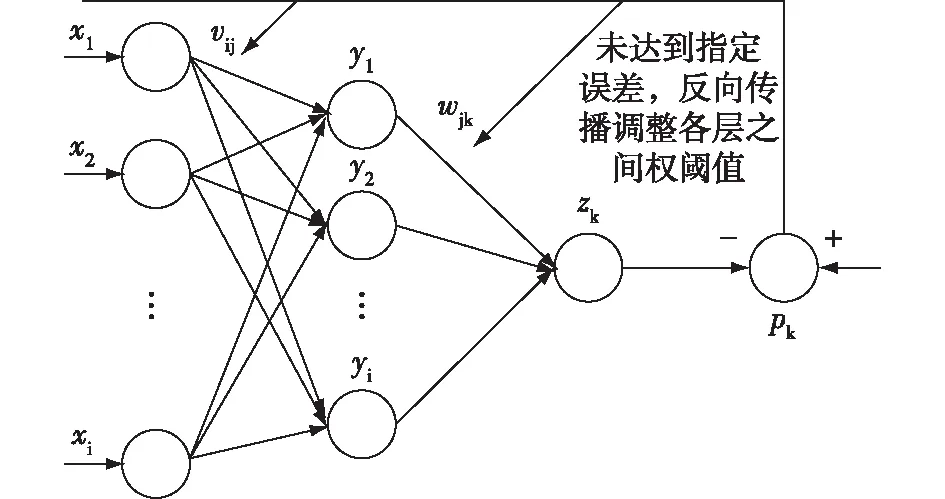
图1 软测量神经网络结构Fig.1 Neural network structure of soft measurement

以磨煤机进出口压差、进口一次风量、进口一次风压、进口一次风温、出口风粉压力、出口风粉温度、磨煤机电流数据为输入层xi,隐含层为yj,出粉量为输出层zk,出粉量的期望输出为pk,vij和wjk分别为输入层与隐含层、隐含层与输出层之间的连接权阈值。BP神经网络连接权阈值通常是在[0,1]范围内随机选取,而该选取方式导致算法收敛减慢且易陷入局部最佳值。普通粒子群算法将鸟群模型中鸟类的栖息地比作所求问题空间中的可能解的位置,通过粒子间信息传递,引导整体粒子向可能解方向移动,在此过程中逐步发现最佳解[15]。通过融合策略改进粒子群算法，从BP神经网络权阈值空间中搜寻全局最佳权阈值，并赋予BP神经网络作为初始权阈值,构建磨煤机参数和出粉量之间的软测量模型,得到最优出粉量预测值,并以此模型对参数进行优化。

1.2 融合策略优化BP神经网络软测量算法

1.2.1 小生境方法提高种群多样性

若某个粒子在连续多次迭代中适应度变化量很小,为保证迭代中粒子群算法的多样性,通过以该粒子为中心,以该粒子和距该粒子最近的粒子之间的距离为半径，构造一个圆形小生境[16]。则小生境子粒子群(Sj)半径(Rj)定义为

Rj=max{‖xj,g-xj,i‖}

(1)

式中:xj,g和xj,i分别为小生境子粒子群中最优粒子(Sj,g)和其他非最优粒子(Sj,i)的半径。

在算法运行过程中,若‖xi-xj,i‖≤Rj(xi为粒子i的半径),则代表该粒子进入了Sj覆盖范围,该粒子就会被该小生境子粒子群所吸收。同时,若两个子粒子群最优粒子距离≤子粒子群的半径之差,则代表两个子粒子群相交,需要将两个子粒子群合并。

划分完小生境群体后,首先对每个子粒子群采用粒子群算法进行计算,得到各子粒子群最优值,该最优值只代表当前子粒子群。随后更新群体,计算各子粒子群适应度,淘汰适应度过低的粒子,同时若有粒子或子粒子群进入Sj覆盖范围或两个子粒子群相交,则吸收粒子或合并相应子粒子群。最后再对新形成的小生境子粒子群采用粒子群算法迭代计算,重复以上步骤直到完成迭代次数或得到满足要求的结果。具体步骤:

①初始化粒子群群体;

②找到中心粒子并确定半径,划分小生境子粒子群;

③使用粒子群算法迭代划分后的子粒子群,得到子粒子群最优值,并更新子粒子群;

④计算各子粒子群适应度,淘汰适应度低的粒子,吸收进入小生境子粒子群半径范围的粒子,合并相交的子粒子群;

⑤更新小生境子粒子群,并重复进行步骤③和④直至达到迭代次数或满足精度要求。

该算法较传统的粒子群算法在维持种群的多样性方面有了很大的提升,可以提高收敛成功率，并能有效减少收敛时间。但是该算法中使用了传统粒子群算法的迭代方法,在迭代中会因为其他参数的影响陷入局部最优解,所以需要对算法进行进一步优化。

1.2.2 惯性权重的动态调整

由于传统粒子群算法的惯性权重通常是线性变化或不变的,而缺陷识别模型的输入与输出关系是复杂非线性关系,采用线性函数调整惯性权重会导致粒子的启发性无法提高,导致算法陷入局部最优解,无法获得准确的迭代数据。为了提高粒子的搜索能力,本文采用动态调整的非线性惯性权重公式代替原有的惯性权重公式,从而提高粒子的搜索能力、算法的效率以及精度。

以Sigmod函数为参考，并配合惯性权重的特征,使该函数能更好地调整惯性权重,将Sigmod函数变形套用于惯性权重(w)的变化，如式(2)所示。

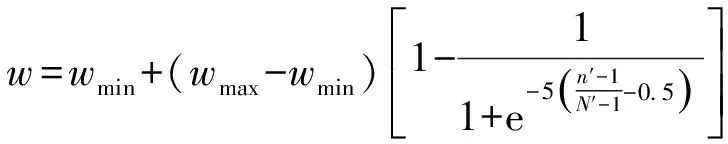
(2)

式中：wmax为惯性权重最大取值,wmin为惯性权重最小取值,N′是迭代总次数,n′为当前迭代次数。

虽然使用该方法时，由于粒子会出现“靠拢”现象,即粒子都聚集在局部极值点附近,导致该算法陷入局部最优解，但本文算法采用小生境法,将聚拢的粒子划为小生境子粒子群,所得最优解即为子粒子群最优解,避免该算法由于粒子“靠拢”从而陷入局部最优解。该算法能有效地提高粒子群算法的精度,但是惯性权重的非线性变化会导致学习因子难以与算法进程统一,同时为了提高搜索速度,需要对学习因子进行调整。

1.2.3 时间因子的调整

在进化迭代过程中,惯性权重与学习因子往往是各自单独调整的,从而导致算法迭代中统一性较弱,对于复杂的非线性迭代来说,会导致迭代过程变得困难,影响搜索时间和模型的识别精度。因此,用惯性权重的变化来控制学习因子的变化,增强惯性权重和学习因子之间的关系,能有效提高算法的优化搜索能力。同时,在算法中引入时间因子,使其随着迭代的次数增加而能有效控制粒子飞行速度,加快搜索效率,提高粒子搜索能力。

在粒子群算法中,粒子是以一定的飞行速度来寻找全局最优解的,在这个过程中,粒子是基于学习和认知来更新自身的速度与位置,而学习因子c1与c2则通过影响粒子的社会学习和自我认知,从而对其运行轨迹进行控制。若设置的学习因子c1过大则会导致粒子在局部范围内活动；c2设置过大则会导致粒子“早熟”,收敛于局部极小值。为了保证学习因子的合理设置,同时为了保证学习因子与惯性权重的一致性,采用式(3)和(4)更新学习因子。

c1=c1s-(c1s-c1e)cosw

(3)

c2=c2s+(c2s-c2e)cosw

(4)

式中:c1s、c2s分别为学习因子的初始值,c1e、c2e分别为学习因子的终止值。

以此方式更新学习因子不仅能加强粒子与惯性权重之间的统一性,有效适应复杂的非线性优化；在前期的迭代中提高搜索速度,增强全局搜索能力;在后期迭代中加强粒子社会学习能力,得到较高精度的全局最优解,提高迭代的精度。

同时,在粒子群算法中,粒子位置更新是以当前位置与当前速度之和来计算下一个位置的。然而速度和位置的量纲不同,不可以直接进行运算,将速度和时间相乘才能够表示距离，从而与位置进行计算,所以在传统粒子群算法中其实也包含了时间量纲,只不过在传统粒子群中将时间因子默认为1,该做法会导致粒子在最优解附近来回震荡。因此，为了改变粒子的时间参数,提高粒子搜索能力,在粒子群算法位置更新中加入时间因子(T),如式(5)所示。

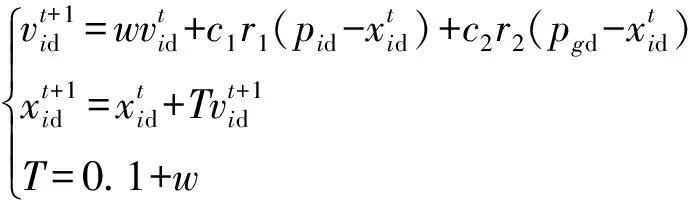
(5)

式中:vid为当前速度,xid为当前位置,t为当前时刻,pid为当前粒子位置,pgd为上一时刻粒子位置,r1、r2为常数。

将T和w相关联,使时间因子随着惯性权重的变化而变化,由于w是非线性减小的,迭代初期，w较大导致T也较大,能有效进行快速全局搜索;而迭代后期，T会越来越小,有利于粒子在局部进行全面搜索,找到全局最优点。

利用该算法设计的磨煤机出粉量软测量模型如图2所示。

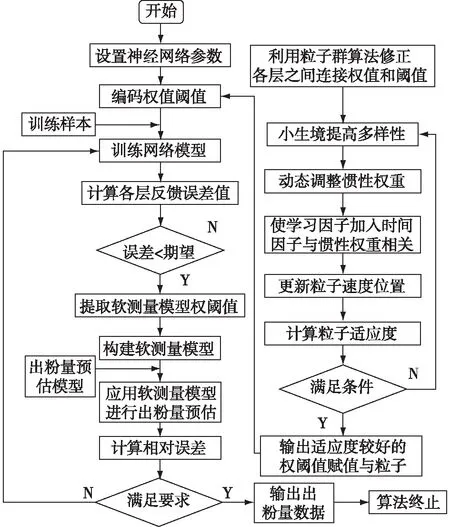
图2 磨煤机出粉量软测量模型Fig.2 Soft measurement model of pulverized coal mill output

2 出粉量软测量实验

2.1 实验数据获取

本文的研究对象为句容某电厂1#磨煤机,通过数据服务器SCADA,从电厂DCS数据库中采集了该磨煤机10 d的历史运行数据,共11 748组数据,从中筛选每天10组，共100组数据作为样本,这些数据采自具有代表性的不同时间段和工况条件,且基本覆盖了该磨煤机各参数的变化范围。

2.2 算法参数设置与对比

从样本数据中随机选取80组数据作为模型的训练样本,剩下20组数据作为模型的测试样本,建立磨煤机出粉量软测量模型。在MATLAB软件中进行融合策略粒子群改进BP神经网络软测量实验[17]。BP神经网络参数设置:神经网络层数设置为3,分别为输入层、隐含层和输出层,输入层输入个数为7(磨煤机各参数),输出层输出个数为1(出粉量)。根据经验公式K=2k+1(K为隐含层节点数,k为变量数),隐含层节点数取为15;学习率较小,虽会牺牲计算速度但会提高算法的精度，故设置为0.1;由于需要达到足够精度,所以神经网络训练次数设为10 000次;训练误差即为精度，设置为10-6。融合策略粒子群算法参数设置:种群规模设置为50;wmax=0.9,wmin=0.5;w按照式(2)动态变化;学习因子设置为c1s=c2s=2,c1e=c2e=1。

2.3 计算结果分析

基于融合策略改进的粒子群(PSO)优化BP算法(PSO-BP)模型预测磨煤机出粉量，并与实际值进行对比，结果如图3所示,绝对误差如图4所示,算法迭代过程如图5所示。

图3 融合策略改进PSO-BP模型的磨煤机出粉量预测值和实际值对比Fig.3 Comparisons between predicted coal mill based on PSO-BP model with fusion strategy and pulverized coal mill yield

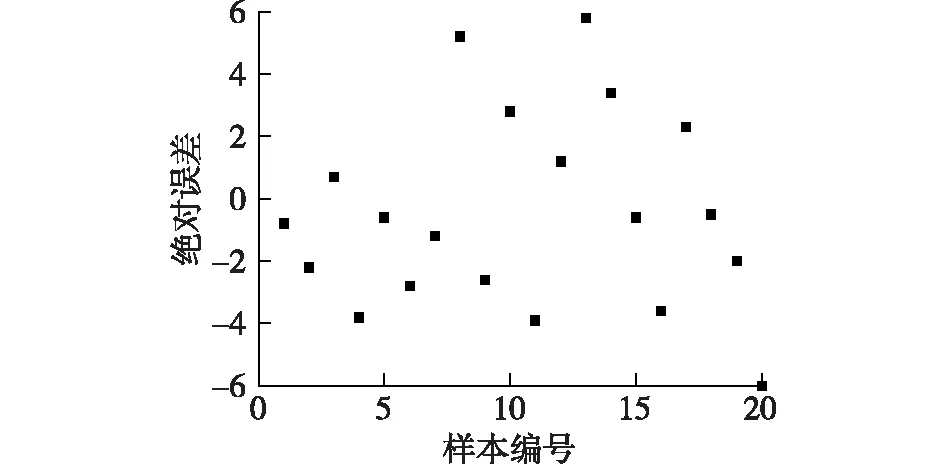
图4 融合策略改进PSO-BP模型的磨煤机出粉量绝对误差Fig.4 Absolutely error of pulverized coal mill output based on PSO-BP model with fusion strategy

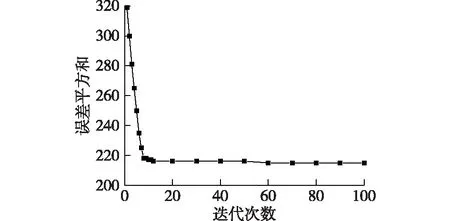
图5 融合策略改进PSO-BP算法迭代寻优效果Fig.5 Iterative optimization effect of PSO-BP algorithm with fusion strategy

由图5可知：融合策略改进PSO-BP算法仅通过10次左右的迭代便基本达到了训练精度,在通过50次迭代之后便基本达到了设定精度,可见该算法可有效提高粒子群的寻优能力。通过设定较高的初始惯性权重和学习因子可使算法在迭代初期快速进行全局搜索,并且由小生境法保证粒子种群多样性,避免算法陷入局部最优解,从而可快速找到全局最优区域,即10次左右迭代便基本锁定全局最优区域。在寻找到全局最优区域后,依据迭代进程降低惯性权重和学习因子并加入调整的时间因子(式(5)),保证算法在局部的搜索精度,准确找到全局最优解,避免了在全局最优区域的多次重复迭代,有效减少了迭代次数,即在50次左右即搜寻到全局最优解,达到设定精度。同时,最终得到的出粉量预测值与实际值平均相对误差为3.813 9%,表明该算法对于误差的控制较为出色。

为了验证模型的泛化能力和寻优精度,利用所建模型对磨煤机出粉量进行仿真,并将该模型的仿真结果与传统PSO-BP模型和BP模型仿真结果进行比较。本文采用均方相对误差、平均绝对误差、平均相对误差和平方相关系数4个统计学检验数据作为模型的评价指标[18],如式(6)—(9)所示。

(6)

(7)

(8)

(9)

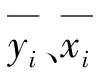
表1为3种模型所得误差结果。由表1可得出:以融合策略改进PSO-BP模型对磨煤机出粉量进行软测量,各项误差均小于传统PSO-BP和BP模型测量值,可见融合策略改进PSO-BP模型精确度较高,在实际应用中效果较好;且融合策略改进PSO-BP模型的R2较其他方法所得结果更加接近1,精度提高较大,更适合磨煤机出粉量的软测量。

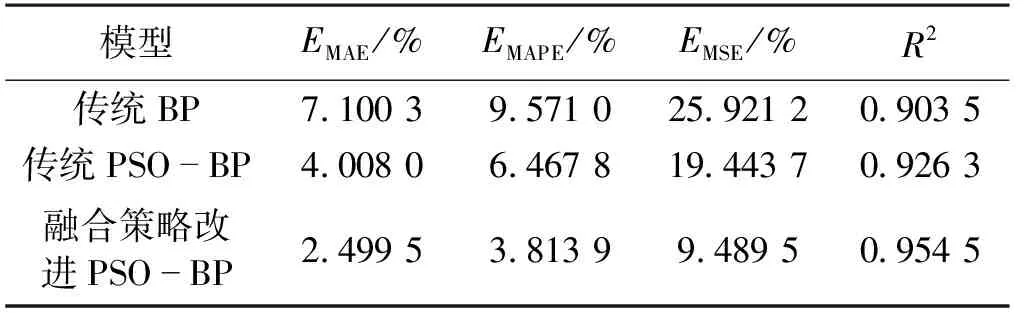
表1 误差对比结果

3 磨煤机出粉量优化

为保证磨煤机在合理工况下运行,同时有效地提高磨煤机的出粉性能,本文提出了基于融合策略改进的粒子群优化BP算法，以磨煤机出粉量模型为基础,选取磨煤机进出口压差、进口一次风量、进口一次风压、进口一次风温、出口风粉压力、出口风粉温度及电流作为模型输入变量,通过磨煤机出粉量模型进行预测,得到磨煤机出粉量这个目标量,利用粒子群算法对其进行寻优,求得最大出粉量和其所对应的运行参数。出粉量的具体优化过程:

①基于磨煤机的型号和工作环境,确定磨煤机运行优化的参数，并采集相应数据;

②采用BP神经网络对选出的磨煤机样本点进行学习训练,建立磨煤机出粉量模型;

③利用融合策略粒子群算法对所建出粉量模型寻优,计算其目标函数输出;

④判断算法是否达到给定的迭代次数,若达到则输出寻优结果,结束计算,否则转到步骤③继续进行寻优计算。

选择融合策略改进PSO-BP算法建立磨煤机出粉量预测模型,即磨煤机出粉性能优化目标,如式(10)所示。

maxf(x)x=(x1,x2,…，x7)

(10)

式中:f(x)为磨煤机出粉量,x1为进出口压差,x2为进口一次风量,x3为进口一次风压,x4为进口一次风温,x5为出口风粉压力,x6为出口风粉温度,x7为电流。

根据实际情况,将优化变量约束条件设置为采集到的各变量所有数据的最大值以及最小值,如式(11)所示。

(11)

设置变量范围后,并以第2.2节方式对融合策略粒子群算法进行设置,对磨煤机出粉量进行优化,结果如表2所示,优化过程中迭代次数与出粉量的关系如图6所示。

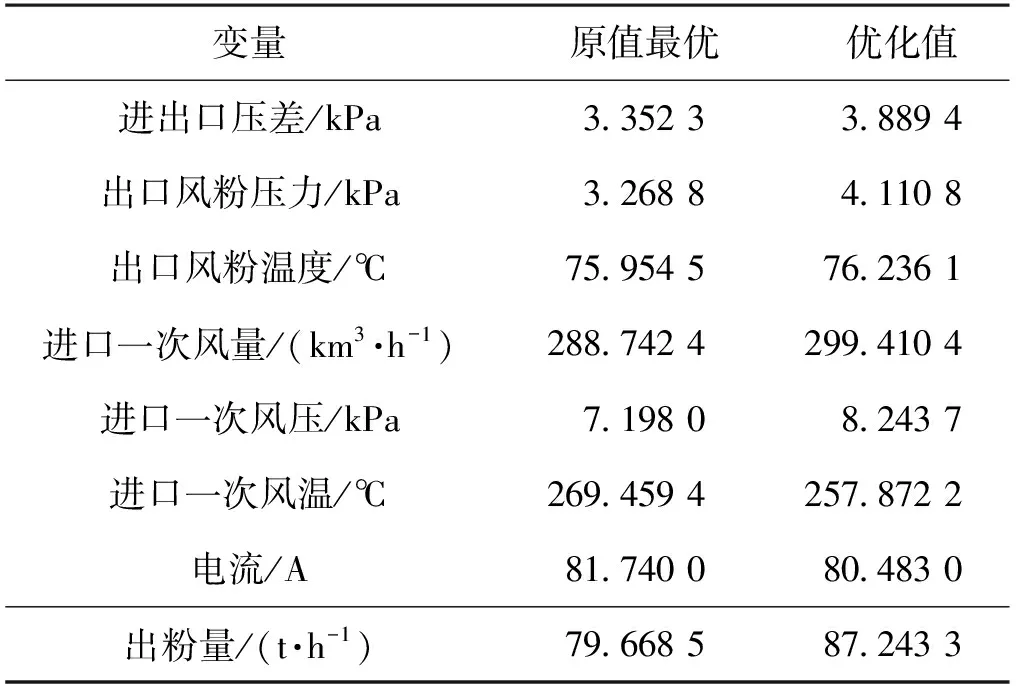
表2 磨煤机出粉量优化结果

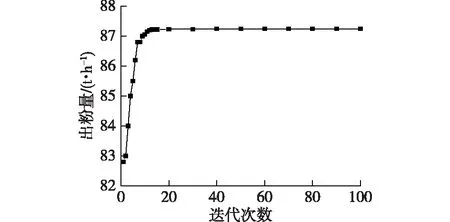
图6 出粉量优化效果Fig.6 Effects of optimizing pulverized coal mill output

由表2可以发现:利用融合策略粒子群算法优化的磨煤机参数中，进出口压差、出口风粉压力、出口风粉温度、进口一次风量、进口一次风压均比采集数据对应的值大,而磨煤机进口一次风温及电流比采集值小,这在一定程度上符合实际生产情况。优化后的出粉量比采集值还高7.574 8 t/h。由图6可看出:通过40次左右的迭代,出粉量基本稳定为87.243 3 t/h,说明基于融合策略改进的PSO-BP算法对磨煤机出粉量进行优化是可行的。由此可见,在实际生产中,按照优化的结果进行生产可以在很大程度上增大出粉量,即可通过在进口处加装鼓风设备或改变进口大小、形状来增大磨煤机进口一次风量和风压;通过改进磨煤机密封系统或通过调整分离器、煤粉分配箱减小磨煤机通风阻力，从而增强进出口压差和出口风粉压力;通过使用高质量的煤或增加燃烧室的氧气可有效提高出口风粉温度;通过给水方式调节进口一次风温;通过改变电路电阻的方式调节电流。

4 结论

1)通过采集磨煤机进出口压差、进口一次风量、进口一次风压、进口一次风温、出口风粉压力、出口风粉温度及电流参数对出粉量进行软测量,预估磨煤机出粉量。

2)以融合策略改进PSO-BP算法进行出粉量软测量建模,以采集的磨煤机参数为输入样本,出粉量为输出样本进行训练,最后以20组数据进行软测量模型的测试。试验结果表明：融合策略改进PSO-BP神经网络软测量模型的平均相对误差仅为3.813 9%,有较好的精度。同时通过与传统BP模型和PSO-BP模型进行对比,进一步地体现了本文算法的优越性和精确性。

3)以融合策略改进PSO-BP算法对磨煤机出粉量进行优化研究,通过设置磨煤机各参数的范围,并以各参数为输入,出粉量为输出,建立优化出粉量模型,从而优化磨煤机的出粉性能。通过适当提高进出口压差、出口风粉压力、出口风粉温度、进口一次风量、进口一次风压和降低进口一次风温、电流,能有效提高磨煤机的出粉量,计算实例表明，最终得出的出粉量提高了7.574 8 t/h,证明本文算法在磨煤机出粉量优化中的可行性和优越性。