计及逆变回馈装置间歇工作制的城轨供电计算

刘 炜 ，李 由 ，张 戬 ，张 浩 ，张 岩

（1. 西南交通大学电气工程学院, 四川 成都611756；2. 新风光电子科技股份有限公司, 山东 济宁 272500）

我国城市轨道交通的发展规模不断增大，有关再生制动能量利用的探讨也逐渐增多. 逆变回馈型再生制动能量利用装置不仅节能效果好、运营成本低，而且能够有效抑制直流牵引网电压波动，因此被新建地铁线路广泛投入使用[1]. 《中国城市轨道交通智慧城轨发展纲要》中对2025年城市轨道交通的发展提出了目标，将再生制动能量综合管理与再利用技术得到广泛推广应用[2].

有关含逆变回馈装置的城市轨道牵引供电系统计算算法的研究日益成熟，但仍有不足. 文献[3]将供电系统中牵引变电所的整流机组与逆变回馈装置等效成晶闸管换流器模型进行建模，并利用交直流交替迭代的方法进行供电计算，但晶闸管换流器模型的母线电压方向在逆变回馈装置处于逆变工作状态时是变化的，与实际的逆变装置工作特性不符；文献[4-5]将供电系统中的逆变回馈装置等效成电压源型换流器进行建模，更准确一些，但此算法被应用在高压直流输电系统，其负荷建模方式与城轨供电系统中的负荷建模有较大差别；文献[6]在直流铁路网络中考虑了含有整流机组与逆变回馈装置的建模，以功率流模拟其工作特性；文献[7-8]在城轨供电系统中，在考虑了逆变回馈装置的情况下，分别提出了交直流混合、交直流统一的潮流计算算法. 虽然现阶段已有很多文献对含有逆变回馈装置的供电系统进行建模与分析，但在仿真与计算过程中均未考虑逆变回馈装置的间歇工作特性，这会导致在逆变回馈装置利用率高的情况下，计算结果与实际出现一定偏差.

目前，有关供电系统节能效果影响因素的研究大多集中在列车运行以及逆变回馈装置的安装位置及容量设置上. 文献[9]采用引力搜索算法优化列车运行图，使系统中再生制动能量的利用效果更好；文献[10]建立考虑了总能耗、制动损耗和逆变装置费用的成本函数，选取逆变回馈装置合适的安装容量，优化逆变装置运行特性；文献[11]考虑了供电系统中压能馈装置容量的影响，提出了基于遗传算法的车-地配合参数优化方法，从而使再生制动能量利用率最大化；文献[12]通过免疫算法选取系统中最佳逆变回馈装置的安装位置. 但以上文献均未考虑整流机组空载电压对系统中再生制动能量分配的影响.

逆变回馈装置在实际运行过程中采用间歇工作制，当通过供电计算来对逆变回馈装置进行选址和容量设计过程中，考虑逆变回馈装置的工作特性模型可以使计算结果与实际情况更加吻合. 为解决上述研究中存在的不足，本文考虑了逆变回馈装置的间歇工作制，基于逆变回馈装置的功率提出了逆变回馈装置负荷过程的动态调整策略，并将其应用于城市轨道供电系统交直流交替迭代的潮流计算，实现逆变回馈装置的状态切换，使负荷过程与实际更加吻合. 以某地铁实际工程为算例，验证了改进的算法与实际工程中逆变回馈装置的负荷过程更加吻合；从主变电所统计整条线路的全日能耗，分析投入逆变回馈装置后，不同逆变回馈装置启动电压、整流机组空载电压和列车发车对数对城市轨道供电系统能耗的影响.

1 逆变回馈装置的工作特性

1.1 逆变回馈装置的间歇工作制

逆变回馈装置以周期工作的方式运行，其间歇工作制是指每个周期内包括一段时间运行和一段时间待机状态的工作方式[13]. 常见的3种工作制分别为矩形工作制（Ⅰ型）、三角形工作制（Ⅱ型）和梯形工作制（Ⅲ型），不同工作制的相关参数如表1所示.其中：I为逆变回馈装置的直流电流；t为时刻；T为逆变回馈装置的一个工作周期；ton为逆变回馈装置在工作周期内的运行时间；Ir为逆变回馈装置的峰值电流；In为逆变回馈装置的持续工作电流；σn为逆变回馈装置的额定占空比. 国内通常使用占空比固定的矩形工作制，即Ⅰ型工作制，该工作制下σn为25.0%.

表1 逆变回馈装置工作制Tab. 1 Working strategy of inverter feedback devices

1.2 考虑间歇工作制的逆变回馈装置负荷过程动态调整策略

逆变回馈装置Ⅰ型工作制下的工作特性曲线如图1所示.

图1中：Ud、Id分别表示牵引变电所（下文简称“牵引所”）直流侧的电压和电流，Id值为负表示逆变回馈装置以逆变状态工作；Ud0为整流机组直流侧的理想空载电压；Uset为设置的逆变回馈装置启动电压；Ur为逆变回馈装置允许的最大工作电压. 当Ud在Ud0与Uset之间（AB段），牵引所中整流机组处于关断状态STOFF，且逆变回馈装置也未启动. 逆变回馈装置有两种工作状态：恒压运行SEFSU（BC段）与恒流运行SEFSI（CD段）. 当Ud达到Uset时，逆变

图1 逆变回馈装置工作特性曲线Fig. 1 Working characteristic curve of inverter feedback devices

回馈装置投入，并将再生制动能量回馈至交流供电网络，此时，牵引网网压始终稳定在Uset，逆变回馈装置工作在SEFSU. 当牵引网上列车继续制动，再生制动能量增多，逆变回馈装置持续工作，当Id达到Ir时(工作点C），逆变回馈装置进入SEFSI，此时，Id恒定. 牵引网中剩余的再生制动能量可能继续抬升直流网压，直到Ud达到Ur时（工作点D），逆变回馈装置启动过压保护不再工作.

考虑逆变回馈装置的间歇工作制后，在固定时间间隔下对装置直流侧允许的最大工作电流进行计算，该时间间隔记为ts. 逆变回馈装置在一个工作周期T内的功率有效值PRMS如式（1）.

式中：ti为第i个运行时刻；Pt为逆变回馈装置在时刻t的功率；Udt、Idt分别为逆变装置直流侧在时刻t的电压与电流.

以逆变回馈装置的额定容量SN为基准，定义装置一个周期内的占空比 σ为

当考虑逆变回馈装置的间歇工作制时，其每一时刻的工作情况均应满足 σ ≤σn.

定义Pmax,j为第j个牵引所中逆变回馈装置在ti至ti+ts时间内未达到 σn时允许的最大运行功率，其计算方法如式（3）所示.

假设在ti至ti+ts时间内Pmax,j=UsetIr，计算得到第j个牵引所中逆变回馈装置在一个工作周期内的占空比为.

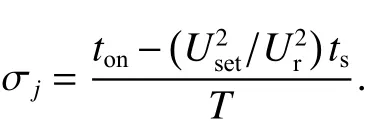
以ts为时间间隔，基于 σj与Pmax,j对第j个牵引所中逆变回馈装置的负荷过程进行动态调整，其策略如式（4）所示.

式中：Idj(ti)为时刻ti第j个牵引所中逆变回馈装置直流侧允许的最大工作电流.

2 考虑逆变回馈装置间歇工作制的城市轨道供电计算

2.1 供电计算模型

对城轨牵引供电系统建模，主要考虑牵引所、牵引网与列车等部分.

牵引所中24脉波整流机组采用多折线外特性工作曲线，通过理想电压源与电阻串联的戴维南等效电路对其进行建模.

对于牵引所中的逆变回馈装置的工作状态，当其为SEFSU时，逆变回馈装置采用理想电压源模型[8]；当其为SEFSI时，逆变回馈装置采用理想电流源模型.为使逆变回馈装置的占空比始终满足其间歇工作制的规定，每次供电计算迭代结束后通过式（4）计算逆变回馈装置该时刻直流侧的Idj(ti). 当逆变回馈装置工作在SEFSU状态时，以重新计算得到的Idj(ti)值对逆变回馈装置峰值电流进行动态限制；当逆变回馈装置工作在SEFSI状态时，以重新计算得到的Idj(ti)值更新时刻ti第j个牵引所在潮流计算矩阵中的电流值，并进行下一步计算.

牵引网包括馈线、上下行接触网、上下行钢轨、回流导线等，本文选取“接触网、钢轨、地”3层地网模型进行建模.

列车在供电计算时通常被等效为电流源或功率源[14-15]，为了提高计算的准确性，本文采用功率源模型对列车进行建模. 仿真过程中，列车每ts的功率恒定，通过牵引网网压求得列车时刻tits的电流值.

2.2 逆变回馈装置的启动电压

列车制动时，产生的再生制动能量通过牵引网给邻近牵引列车使用，或通过逆变回馈装置反馈至交流供电系统，当列车处牵引网网压达到车载制动电阻启动电压Uon时，车载制动电阻启动，消耗多余的再生制动能量.

Uset设置在Ud0和Uon之间，如式（5）所示.

式中：β为逆变回馈装置的启动电压系数，β∈(0,1).

针对整流机组空载电压不同的系统，β的选取影响逆变回馈装置的启动电压，进而影响逆变回馈装置、线路中相邻牵引列车以及车载制动电阻对再生制动能量的利用，从而影响再生制动能量的利用率.

每小时发车对数为Cs，当逆变回馈装置在供电系统中大规模应用时，以主变电所全日能耗W作为供电系统能耗指标，如式（6）所示.

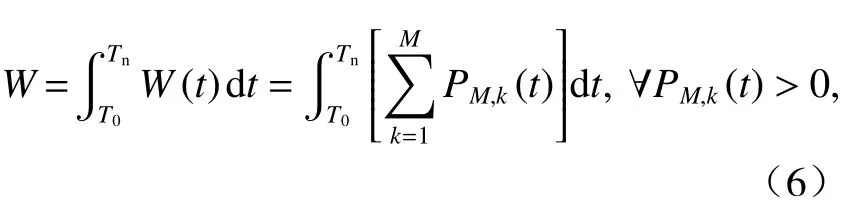
式中：PM,k(t)为第k个主变电所时刻t从电力系统获取的有功功率；M为主变电所数量；T0和Tn分别为列车运行开始和结束的时间.

从主变电所统计能耗不仅包括供电系统中牵引所、牵引网、列车的能耗，也包含了城市轨道中压网络动照负荷的能耗，同时，线路损耗、逆变回馈装置效率等再生制动能量利用过程中的损耗也均被考虑在内. 通过比较W的大小可反映不同β、不同Cs对整个供电系统节能效果的影响.

2.3 供电计算流程

采用交直流交替迭代法[8]对城市轨道供电系统进行求解. 在供电计算中，逆变回馈装置考虑间歇工作制，采用负荷过程动态调整策略，同时考虑了逆变回馈装置运行状态的切换以及车载制动电阻的启动. 改进的城市轨道交直流供电计算算法流程如图2所示.

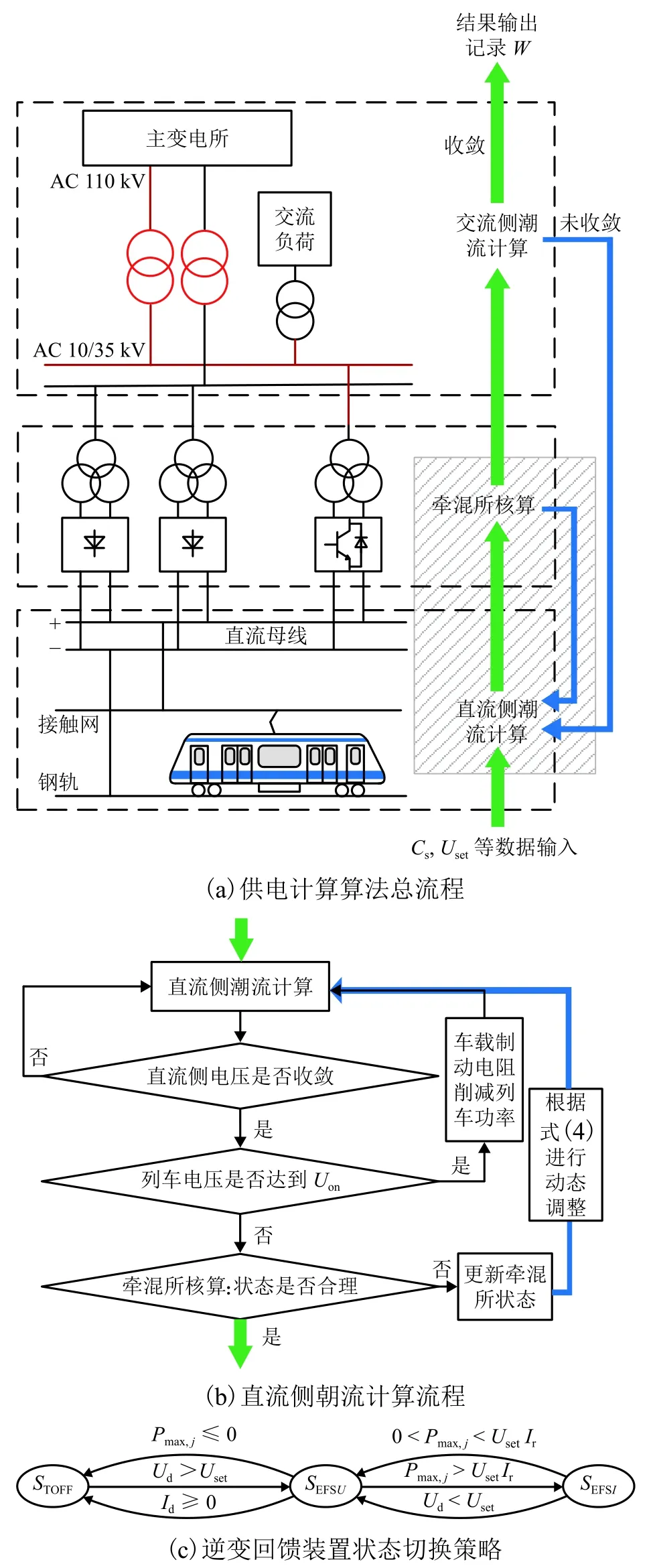
图2 改进的城市轨道交直流供电计算算法流程Fig. 2 Improved algorithm flow of urban rail AC/DC power supply calculation

图2中（a）为供电计算算法的总流程，在对供电系统直流侧进行潮流计算并对牵引降压混合所（下文简称“牵混所”）状态进行核算时，其具体流程如图2（b）所示，当直流侧电压收敛且不超过Uon时，对牵混所的状态进行核算与更新，此时逆变回馈装置的状态切换策略如图2（c）所示. 若牵混所中逆变回馈装置工作，在考虑装置间歇工作制后，为满足其占空比限制，根据式（4）对逆变装置的工作状态进行动态调整，从而使下一个ts的仿真结果与实际更吻合.

3 算 例

以广州地铁某实际工程为计算实例. 该工程开通段长度26 km，采用6辆编组B型车，4动2拖，列车最高运行速度120 km/h，列车额定载重291.8 t.全线共2个主变电所，10个牵混所，其中2个为区间所（牵引所 ⑦、⑧），9个车站. 该线路供电系统简图如图3所示.

图3 广州地铁某实际线路供电系统简图Fig. 3 Outline of power supply system of an actual Guangzhou metro line

3.1 考虑逆变回馈装置间歇工作制前后城市轨道供电系统算法及工程实测的比较

为评估该线路中逆变回馈装置的运行性能，课题组对装有逆变回馈装置的3个牵引所进行现场测试并监测装置的负荷过程，通过在整流机组和逆变回馈装置的直流馈线上安装霍尔电流传感器获得其负荷过程[8].

为比较考虑逆变回馈装置间歇工作制前后的城市轨道供电计算的结果，设置与实际工程相同的仿真条件，分别采用两种算法对供电系统进行仿真，并将结果与实测结果相比较.

该实际工程中，牵引所 ①、⑨、⑩ 设置逆变回馈装置，其中，牵引所 ①、⑨ 的逆变回馈装置安装容量为2 MW，⑩ 的逆变回馈装置安装容量为3 MW，逆变回馈装置启动电压1720 V，发车间隔为525 s. 以牵引所 ⑨ 中逆变装置的某段负荷过程为例，对比改进前后两种算法计算得到的装置直流电流及实测数据统计得到的装置直流电流如图4所示.

从图4可以看出：当运行至第49～64 s时，原始算法由于未考虑逆变装置的间歇工作制，装置仍工作在逆变状态. 改进后算法逆变装置受到工作周期的限制而没有工作，与实际电流曲线更吻合.

图4 算法改进前后及实测的逆变回馈装置直流电流Fig. 4 Measured and calculated DC currents of inverter feedback devices by original algorithm and improved one

改进前后两种算法下及实测数据统计得到的装置占空比曲线如图5所示.

图5 算法改进前后及实测的逆变回馈装置占空比Fig. 5 Measured and calculated duty cycles of inverter feedback device by original algorithm and improved one

从图5可以看出：原始算法由于未考虑逆变回馈装置的间歇工作制，其占空比达到σn后仍继续工作，最高可达27.8%.

实测该牵引所逆变回馈装置反馈电量为164.736 kW•h，改进前该牵引所逆变回馈装置反馈电量为190.818 kW•h，改进后逆变回馈装置反馈电量为177.326 kW•h. 从统计结果来看，考虑逆变回馈装置间歇工作制的城市轨道交直流供电计算与逆变回馈装置的真实运行情况更加吻合.

3.2 不同β、Cs情况下逆变回馈装置节能效果

分别考虑以下两种情况对供电系统进行仿真：

情况1除区间所外全部牵引所安装逆变回馈装置，同时考虑装置的间歇工作制. 该线路中，逆变回馈装置使用表1中的Ⅰ型工作制；

情况2全部牵引所不安装逆变回馈装置.

实际线路中，Uon一般为1790 V. 设置Ud0为1 664 V，改变β的大小从而得到多组Uset，同时设置多组Cs，以发车间隔为周期进行供电仿真，对W进行统计，统计结果如图6所示.

图6 不同β、Cs情况下的WFig. 6 W varying under differentβ andCs

从统计结果来看，相同Cs下，W随β的增大，先降低后升高. 这是因为，当β过小时，Uset过低，线路中制动列车产生再生制动能量时，本能直接通过牵引网给相邻牵引列车利用的再生制动能量被逆变回馈装置吸收，这部分能量通过装置回馈至交流供电系统时产生一定的损耗，甚至会在主变电所处返送电度，导致W增大；当β增大，Uset升高，牵引网网压随之升高，列车运行处网压更易达到Uon，车载制动电阻启动随之增多，W增大. 当β超过0.680，即Uset为1750 V时，W明显增大，此时列车再生制动能量被车载制动电阻大量消耗，造成了制动能量的浪费，逆变回馈装置的节能效果被削弱.

不同Cs下，系统W最低时的β值不完全相同.当Cs为10.00对/h，W在β为0.365时最低，此时Uset为1710 V，情况1相比于相同Cs的情况2系统可多节省12.23%的电量，此时，逆变回馈装置与线路中相邻牵引列车对再生制动能量的利用最合理，更有利于系统的节能. 可见，逆变回馈装置的启动电压会影响列车再生制动能量的利用效果；逆变回馈装置在合适的启动电压下具有更优的节能效果.

3.3 不同Ud0、β情况下逆变回馈装置节能效果

选取与3.2节中相同配置下的情况1与情况2进行仿真. 该地铁线路实际发车间隔为525 s，即Cs为6.86对/h，仿真设置列车发车对数与实际相同，选取多组Ud0，同时改变β的大小，对W进行统计，统计结果如图7所示.

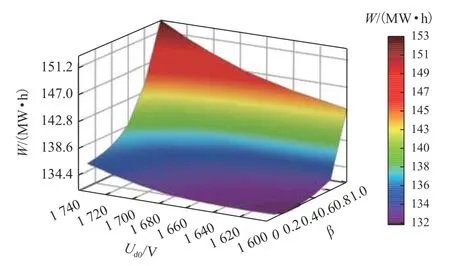
图7 Cs = 6.86时，不同Ud0、β情况下的WFig. 7 W varying under differentUd0 andβ atCs = 6.86

根据地铁线路设计时的远期规划，列车发车更为密集，Cs为20.00对/h，同样改变Ud0与β的大小，进行多组供电仿真，并对W进行统计，统计结果如图8所示.

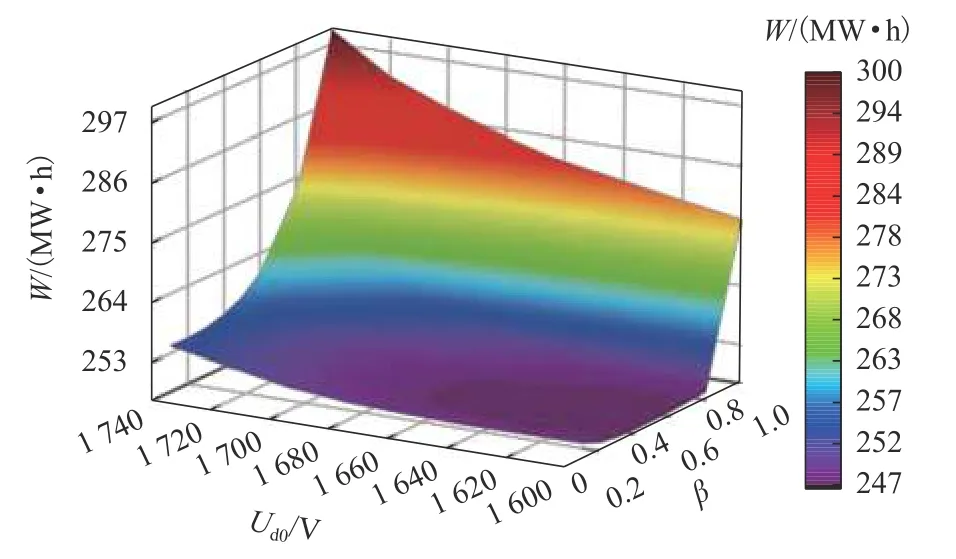
图8 Cs = 20.00时，不同Ud0、β情况下的WFig. 8 W varying under differentUd0 andβ atCs = 20.00

不同Ud0对应系统能耗最低时的β值为βW-min，统计两种Cs下的βW-min，其结果如表2所示.

表2 不同Cs下的βW-min及WTab. 2 βW-min andW under different Cs

对比两种发车对数的结果可以看出：βW-min随Ud0的增加基本呈下降趋势；Cs越小，βW-min整体越低. 当Cs为6.86对/h，βW-min分布在0.100～0.316；当Cs为20.00对/h，βW-min分布在0.200～0.421. 这是由于，当Ud0增加，线路牵引网网压整体抬高，更易达到Uon从而使车载制动电阻介入，此时降低Uset，可以更好地稳定牵引网压，减少车载制动电阻的投入，从而提高逆变回馈装置的节能效果，降低系统能耗，因此βW-min更低；当Cs较小，即发车较为稀疏时，当线路中有列车制动，相邻牵引列车吸收的制动能量较少，为了避免车载制动电阻过多启动，减少制动能量的浪费，Uset应降低，因此βW-min整体更低. 此线路全线牵引所实际Ud0在1680～1720 V波动，根据仿真结果，β选取在0.11～0.18可以使逆变回馈装置在实际运行过程中获得更佳的节能效果.

仿真条件不变，对情况2下两种Cs不同Ud0时的供电系统进行仿真，对比情况1下β为βW-min时的W与情况2下的W，其结果如图9所示.

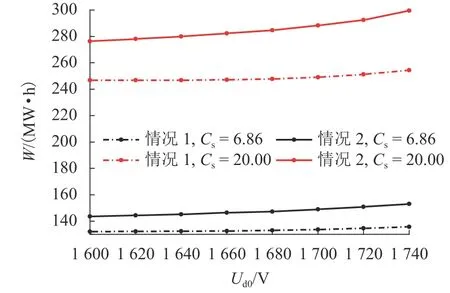
图9 不同Ud0时，情况1下β为βW-min时的W与情况2下的WFig. 9 With differentUd0,W change in case 1 whenβ=βW-min and in case 2

城市轨道牵引供电系统目前广泛使用电缆供电，运营的城市轨道交通线路普遍存在牵引所交流侧电压较高、整流机组空载电压偏高的情况. 从图9可以看出：不同Cs时，情况2下W随Ud0增加呈上升趋势；当Cs为6.86对/h，Ud0为1740 V时的W相比1600 V时增大6.56%，当Cs为20.00对/h，Ud0为1740 V时的W相比1600 V时增大6.98%. 这是由于Ud0增加，全线牵引网网压抬升，虽然可以一定程度上降低供电系统网损，但由于车载制动电阻介入更加频繁，导致再生制动能量利用率变低，W增加.

不同Ud0时，情况1下当β为βW-min，即系统节能效果最好时，相比情况2系统的W，逆变回馈装置的节能率[7]如表3所示.

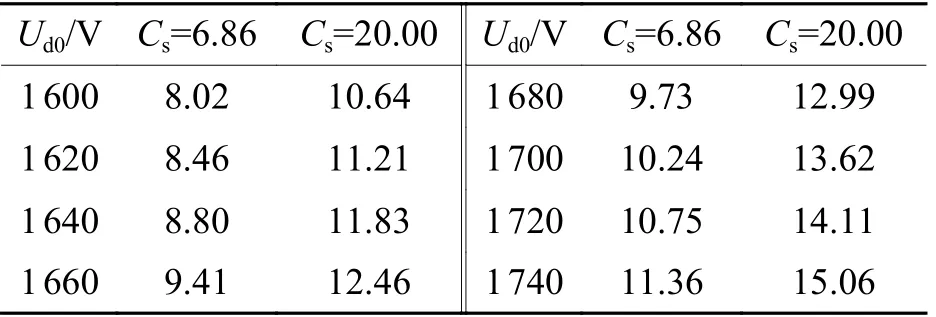
表3 不同Cs下的系统节能率Tab. 3 Energy saving rate of system under differentCs %

从表3可以看出：随着Ud0的增加，逆变回馈装置的节能率提高，Cs为20.00对/h时节能率最高可达15.06%.Ud0越高的场合，逆变回馈装置对系统的节能效果越明显.

4 结 论

本文考虑了逆变回馈装置的间歇工作制，改进了城市轨道交直流供电计算算法. 通过对实际工程进行仿真研究，探讨系统能耗的影响因素，得出结论如下：

1） 本文基于逆变回馈装置的功率提出了逆变回馈装置负荷过程的动态调整策略，并将其应用于城市轨道供电计算算法，使装置负荷过程及占空比变化过程与实际更加吻合.

2） 逆变回馈装置的启动电压会影响供电系统的能耗；整流机组空载电压、列车发车对数均会影响逆变回馈装置最佳启动电压的选取：当空载电压较高，或当发车对数稀少时，适当降低逆变回馈装置的启动电压（较低β值）以获得更佳的节能效果. 当Cs为6.86对/h，Ud0在1600～1740 V变化时，逆变装置最优启动电压系数βW-min在0.100～0.316，Ud0为1740 V时，主变电所能耗W比未安装逆变回馈装置的系统W减少11.36%，；Cs为20对/h，Ud0在1 600～1740 V变化时，βW-min在0.200～0.421，Ud0为1740 V时的W比未安装逆变回馈装置的系统W减少15.06%.