基于高斯过程回归模型的大坝位移预测
庞帅峰 杨利娟 夏占营
(1.自然资源部第七地形测量队,海南 海口 570100; 2.海南天涯人力资源管理服务有限公司,海南 海口 570100;3.河南豫兴测绘有限公司,河南 滑县 456400)
1 引言
近年来国家水利大力发展下,大坝带来了巨大经济效益,但以往发生的与大坝相关的重大安全事故,不仅威胁百姓的人身安全财产,更给国家带来严重的经济损失。随着科学技术的发展及研究人员的不断探索,GNSS、应变传感器、激光测距仪、多点位移计、渗压计等仪器和技术逐渐用于坝体安全自动化监测领域,并在实际工程中不断改进,目前坝体位移监测系统的数据收集、处理、存储等功能均已达到世界先进水平。但由于我国建立坝体安全监测系统时一些开发工作较为落后,国内目前在分析监测资料时仍采用传统的回归模型等。考虑到传统方法的局限性,建立一个有效且精确的坝体安全监控预测模型尤为重要。
早在上世纪20 年代便有人认识到大坝安全的重要性,但由于技术发展所限收效甚微。直到1955 年国外专家学者Rocha 和Fanelli 等人采用统计回归的数学方法分析大坝监测资料。1964 年Silvera[1]引用幂函数作为时效分量,使大坝监测得到进一步发展。1977 年Faneli 等创建了坝体形变的确定性模型和混合模型[2]。1984 年Pedro 等[3]进行定量模拟观测模型。1985 年,高斯-马尔科夫理论被Guedes引入多远线性回归模型。此后Purer等在回归分析中加入效应量的前期观测值,使混合模型计算精度得到很大提高。1991 年熊支荣等基于灰色理论创建了数学模型。2002 年李雪红等提出灰色-时序模型。此后,岳建平等[4]学者基于灰色系统理论,对坝体形变做出精准预测。2003 年张晓春等[5]建立了径向基神经网络(RBF)模型,极大提高了计算效率。随后几年,多位专家学者基于神经网络、灰色理论、模糊聚类分析、粒子群优化算法、卡尔曼滤波等进行了深入研究。2012 年吕开云[6]应用支持向量机建立大坝变形预测模型,并应用于黄河小浪底水利枢纽预测,取得较好的拟合及预测精度。2017 年朱俊[7]从大坝安全的影响因素和必要性出发,对当前大坝安全监测现状进行分析总结。2018 年李洪宇[8]采用高斯过程回归模型,取得了很好的结果。2019 年王申波在高斯过程中通过粒子群算法优化超参数并选择最优协方差函数,取得极高精度。
大坝变形的主要形式有:整体或局部位置随时间变化而发生位移及坝体裂缝等影响坝体正常运行的变形。在温度、渗水、库水压力等外界因素对坝体的长期连续作用下,坝体强度降低,由此产生形变。对于混凝土坝来说,水压、温度是长期影响坝体位移的因素,时效位移不可逆在大坝建成初期形变较明显,随时间增加而稳定,地基稳定性也很重要 ;其次对水压、温度、时效这三大影响因素分别建立坝体位移数学模型。
2 数据来源及预处理
2.1 数据来源
小浪底水利枢纽位于河南省洛阳市孟津县与济源市之间,三门峡水利枢纽下游130 公里、河南省洛阳市以北40 公里的黄河干流上,控制流域面积69.4 万平方公里,占黄河流域面积的92.3%。坝址南岸为孟津县小浪底村,北岸为济源市蓼坞村,是黄河干流三门峡以下唯一能够取得较大库容的控制性工程,既能较好地控制黄河洪水,又可利用其淤沙库容拦截泥沙,进行调水调沙运用,减缓下游河床的淤积抬高。小浪底工程投运以来,发挥了巨大的社会效益、经济效益和生态效益,为保障黄河中下游人民生命财产安全、促进经济社会发展、保护生态环境做出了重大贡献。
小浪底水库正常蓄水位时淹没影响面积277.8km2,施工区占地23.33km2,共涉及河南、山西两省的济源、孟津、新安、渑池、陕县、平陆、夏县、垣曲8 县(市)33 个乡镇,动迁年移民20 万人。因此对该大坝进行安全监测很有必要,在大坝安全监测评价体系中,坝体位移可以很好地反映大坝运行状态,该大坝往年监测资料如表1 所示。

表1 大坝坝顶某点监测点位移量成果
2.2 数据预处理
由于输入X特征的单位(水位、温度、时序)或者大小相差较大,容易影响位移Y的结果,使得一些算法无法学习到其他特征。因此需通过一些转换函数将特征数据转换成更加适合算法模型的特征数据。把原始数据变换到均值为0,标准差为1 范围内:

3 高斯过程回归模型
3.1 高斯过程回归原理

3.2 核函数
由于坝体位移的变化是非线性的,需要将输入X映射到一个更高维的空间中来拟合坝体位移Y,这种将某个特征空间到另一个特征空间的映射通过核函数实现。核函数选择要求满足Mercer 定理,即核函数在样本空间内的任意格拉姆矩阵(核矩阵)为半正定矩阵。可用的核函数包括径向基函数核、马特恩核、有理二次函数核、正弦平方核、点积核等。本文使用正弦平方核进行实验对比。正弦平方核可对周期性函数进行建模,由长度尺度l>0 及周期参数p>0 实现参数化:

4 结果与分析
为验证算法的有效性和适用性,本文将高斯过程回归模型与K 邻近回归模型、回归数模型、随机森林横向对比,计算所有结果并对比预测结果的中误差。
4.1 高斯过程回归分析
高斯过程回归分析中核参数中长度尺度设置为0.01,周期设置为8,长度尺度范围设置为(0,100),周期范围设置为(1,100);高斯过程回归参数中噪声水平设置为0.05,优化器默认为fmin_l_bfgs_b。
模型训练之后测试精度为0.9448,预测精度为0.9764,其中训练最大误差为0.5116dm,测试点最大误差为0.5313dm,预测最大误差为0.4588dm,预测中误差为0.2260dm。程序输出折线图如图1 所示,详细位移误差如表2 所示。
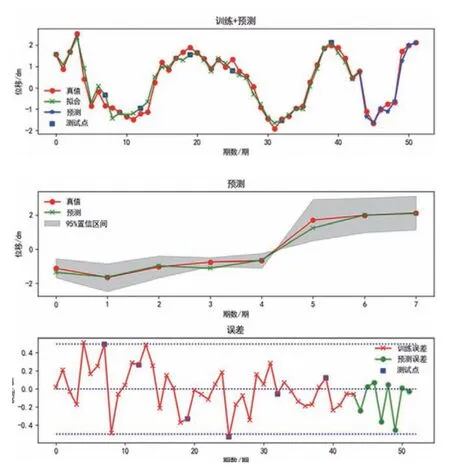
图1 高斯过程回归结果输出
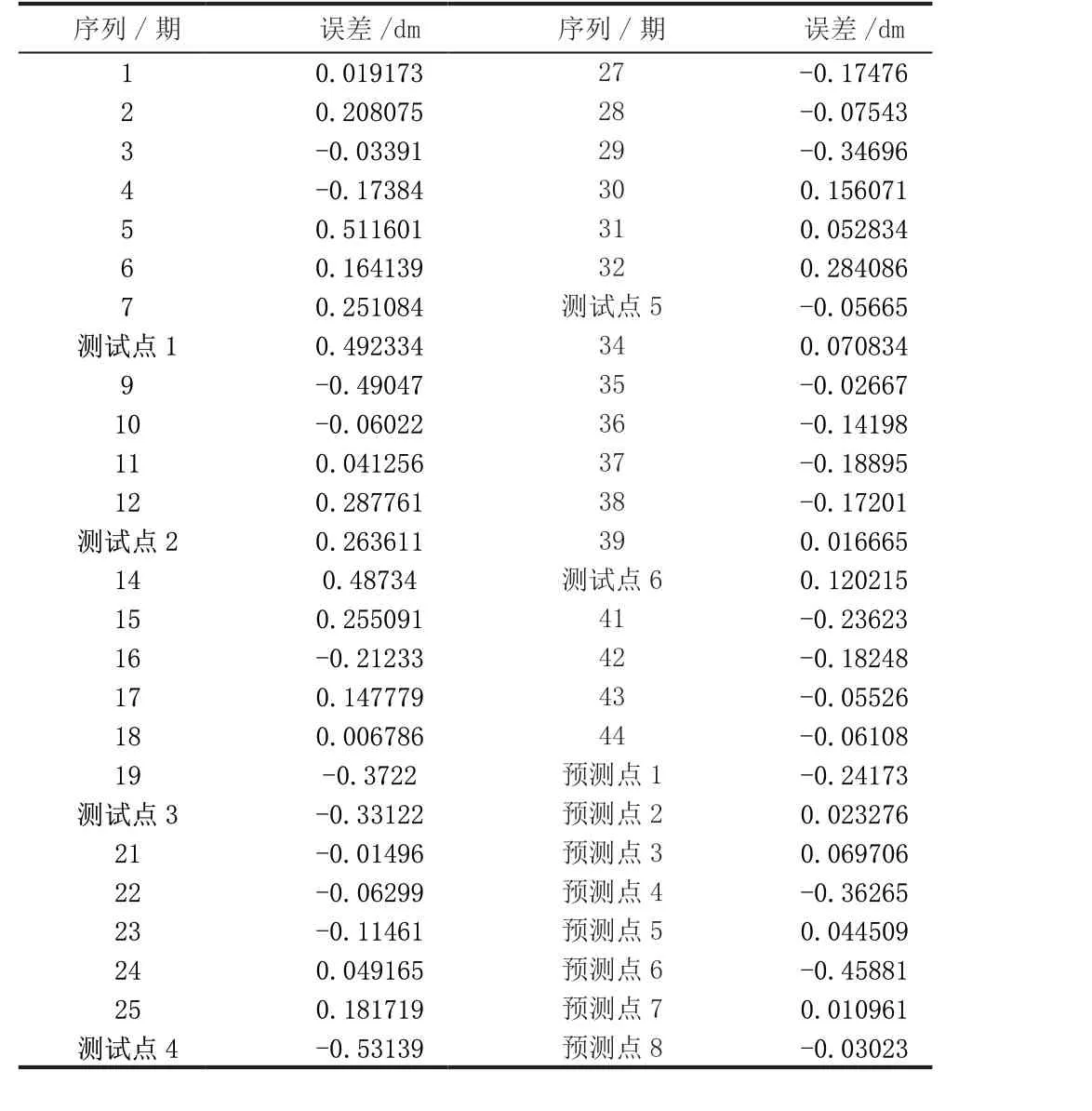
表2 高斯过程回归分析训练及预测误差
4.2 其他回归分析
4.2.1 K 临近回归分析
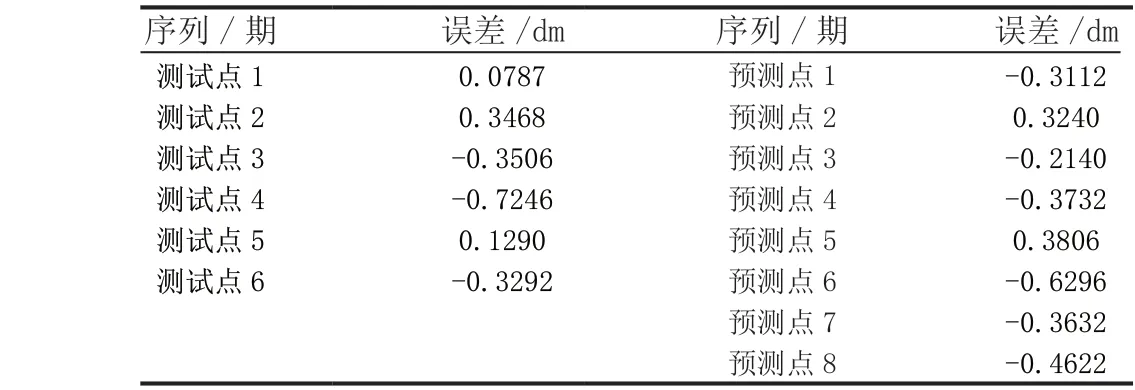
表3 KNR测试及预测误差
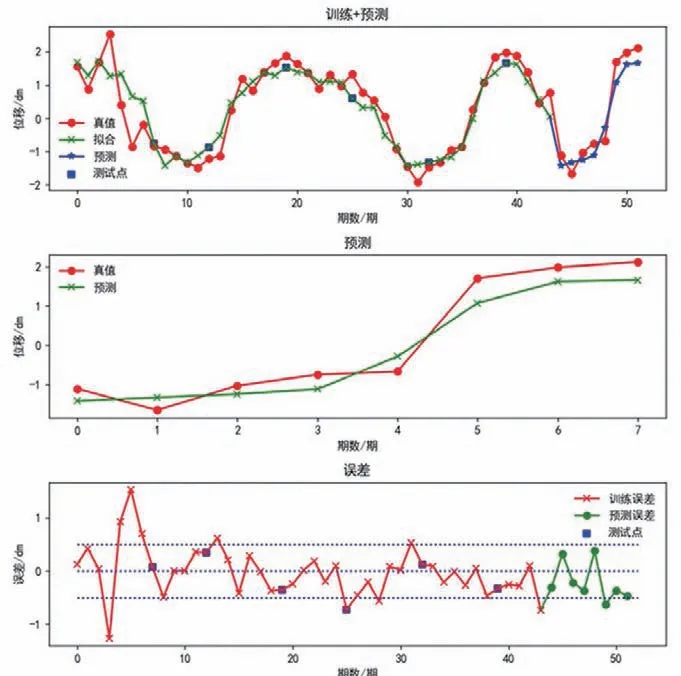
图2 KNR结果输出
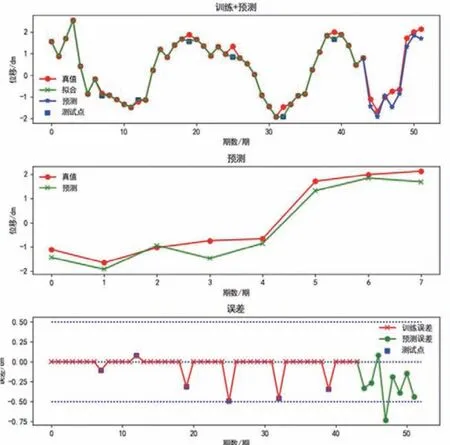
图3 回归树结果输出

图4 随机森林结果输出
采用该方法回归分析,模型训练后测试精度为0.9468,预测精度为0.9351,其中测试点最大误差为0.4960dm,预测最大误差为0.7300dm,预测中误差为0.3845dm。程序输出折线图如图3 所示,详细位移误差如表4 所示。

表4 回归树测试及预测误差
4.2.3 随机森林分析
采用随机森林回归分析,当n_estimators 设置为81 取得较好的结果。模型训练后测试精度为0.9516,预测精度为0.9504,其中测试点最大误差为0.5075dm,预测最大误差为0.5064dm,预测中误差为0.3277dm。程序输出折线图如图4所示,详细位移误差如表5所示。

表5 随机森林测试及预测误差
4.3 对比分析
汇总以上所有结果并计算中误差,结果如表6 所示。
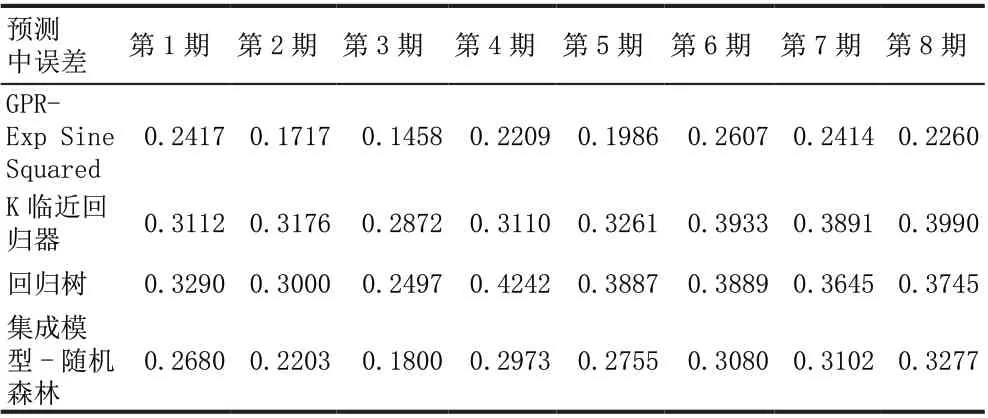
表6 预测中误差对比
对于本研究来说,高斯过程回归在各期相较于其他回归模型预测结果都表现优异。
5 结论
将高斯过程回归方法应用于坝体水平位移预测进行探讨和研究,建立了多个不同内核的高斯过程回归模型,并对结果进行分析,结果表明高斯过程回归在一定程度上能较准确地预测坝体位移。但由于水平及时间所限,研究还不够深入全面,在今后应加强相关理论知识的学习,并在以下两方面开展进一步研究:
(1)高斯过程回归中只进行了单个核函数实验,并未对不同核函数进行对比实验,下一步需对不同核函数进行对比并对模型进行优化;
(2)由于观测资料所限,模型只是针对小浪底坝体某点观测资料,因此模型目前不具有泛化性;下一步需要进一步收集整理该坝体其他观测点数据,以及其他坝型数据资料,不能只局限于混凝土坝。

