容量悬殊道路的交叉口多参数协调控制方法
丁柏群,杨 柳,徐 赫,骆丽珍
(1. 东北林业大学 交通学院, 黑龙江 哈尔滨 150040; 2. 江苏百盛工程咨询有限公司, 江苏 南京 210000;3. 新疆交通建设集团股份有限公司, 新疆 乌鲁木齐 830016)
0 引 言
主次道路交叉口通常采用保障主要道路通行能力的主路优先控制策略;但在主次道路容量差距较大的交叉口,当交通流达到过饱和时,这种控制方式会导致次路车辆随信号周期循环持续累积,排队过长乃至溢出,进而干扰甚至“锁死”上游交叉口,造成局域路网交通控制失灵、交通运行瘫痪。
当过饱和状态持续发展到一定程度时,主次道路交叉口的主要矛盾实际上已经由保障通行效率转换为避免交通中断和均衡交通需求。目前在一些较大城市,双向八车道至十车道以上的主干路日渐增多,这些道路容量很大,可以容纳较多车辆排队;如何充分利用主路容量以控制过饱和交通流导致的次路排队溢出,综合平衡主次道路的交通需求,维持局部路网的交通运行和微循环,是一个值得考虑的问题。
排队溢出现象也可以表述为交通过饱和,X. WU等[1]将交叉口绿灯损失时间和通行效率作为评估过饱和严重度的指标。不同学者对排队长度的计算提出了不同的方法;R. WUNDERLICH等[2]通过计算机模拟预测交叉口呈稳态流时的最大排队长度;P.MIRCHANDANI等[3]以排队论为依据建立车辆呈现稳态分布时排队长度的计算模型;H. LIN[4]在出租车实际定位数据的支持下,计算交叉口的排队长度和延误时间,所得结果适用于非拥堵路况。
在排队长度模型的基础上,多种多参数信号控制策略被提出。K. ABOUDOLAS等[5]将信号控制的各项参数和约束视为二次规划问题,在交叉口平衡各进口道的排队长度;李振龙等[6]以排队长度最短、车辆延误最小、尾气排放量最少为目标建立多目标优化模型,求得最优化配时方案;王进等[7-9]基于相邻关联交叉口的排队长度计算模型,建立了关联交叉口的信号控制优化方案;成卫等[10]提出一种基于感应控制的流量转移方法以解决某方向排队溢出而导致的拥堵问题。
多数对过饱和交叉口的研究集中在利用相邻交叉口的联动协调控制将较大的排队压力分散到上游交叉口,但涉及到主次道路容量悬殊交叉口的多参数协调控制的研究较少。针对次要道路过饱和状态车辆排队过长导致的不利影响,综合协调主次道路交通容量、排队和延误等因素,为容量悬殊道路的交叉口建立针对性控制策略。
1 次要道路红末排队计算模型
在交通波理论和交通流二流理论的基础上建立次路红灯末期排队长度模型,使用VISSIM仿真软件检验模型的可靠性。
1.1 模型建立
1.1.1 单车道模型
信号交叉口进口道内最终排队车辆数等于上周期滞留车辆数与本周期滞留车辆数的总和,如式(1):
ΔN(r+C)=N(r)+N1(r+C)-N2(r+C)
(1)
式中:N(r)为上周期路段滞留车辆数,pcu;N1(r+C)为本周期内进入车辆数,pcu;N2(r+C)为本周期内离去车辆数,pcu;ΔN(r+C)为本周期红灯结束时上下游断面的车辆总数,pcu。
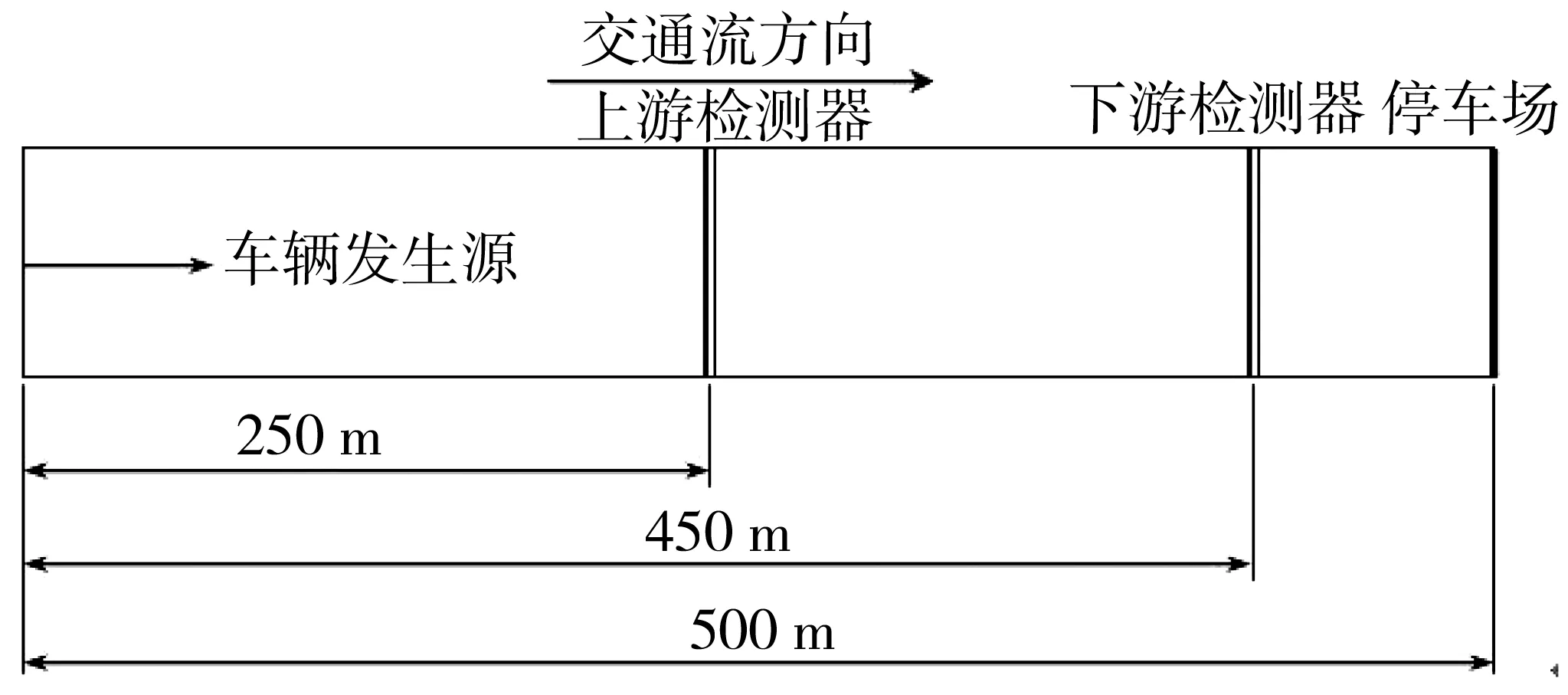
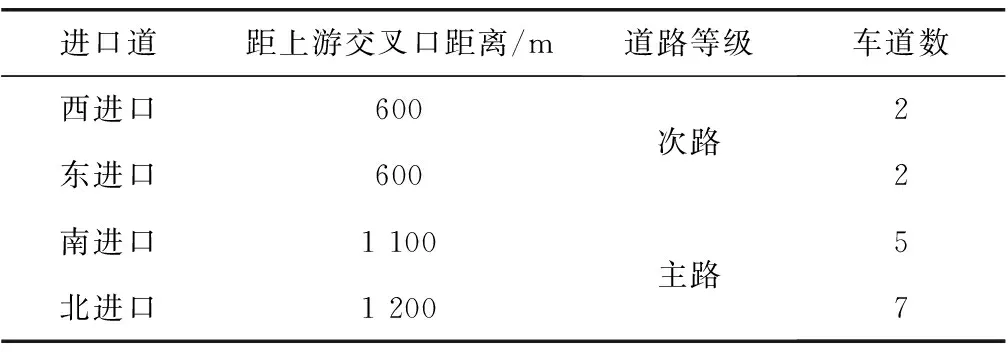
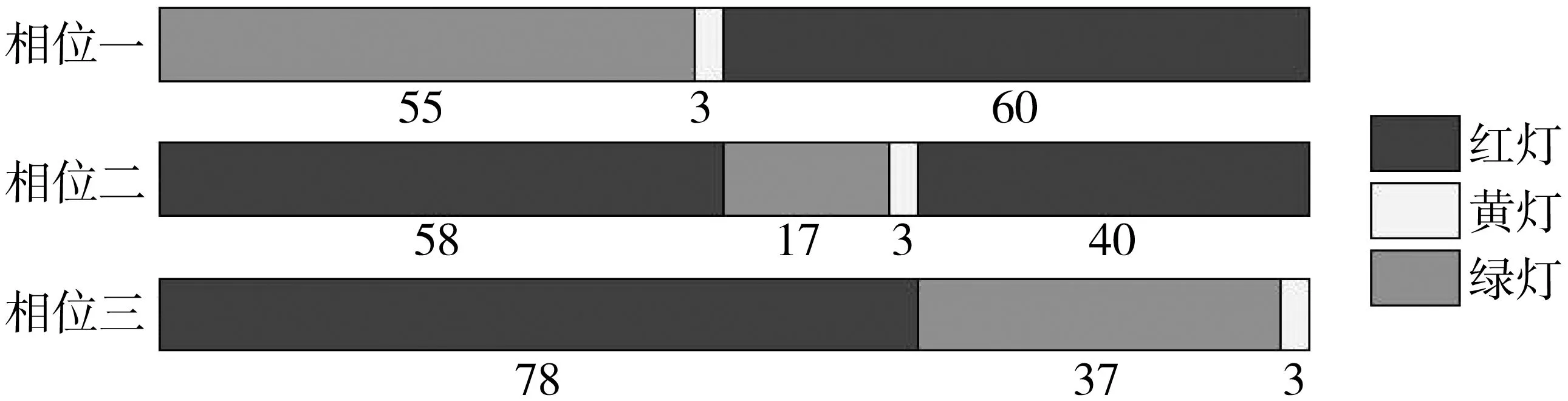
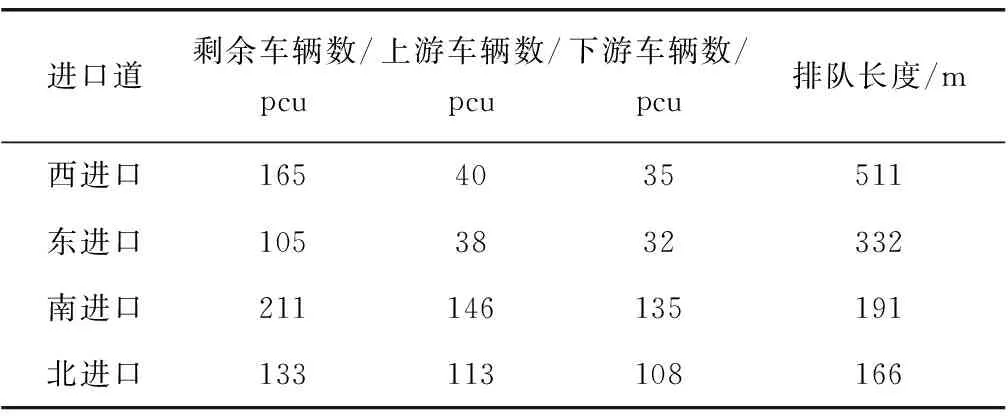
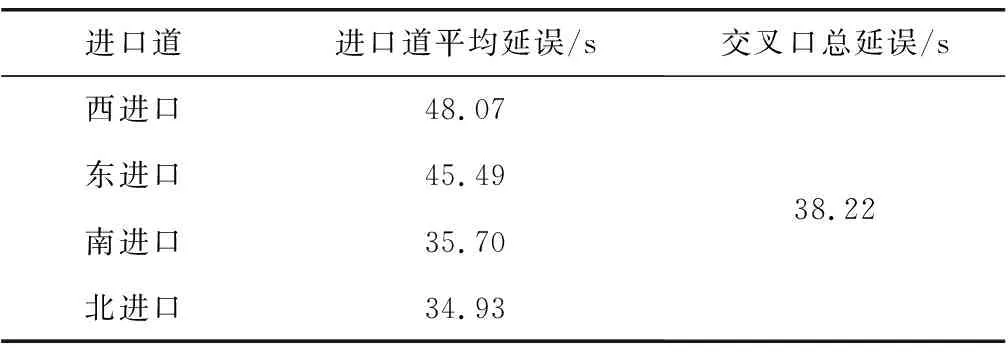
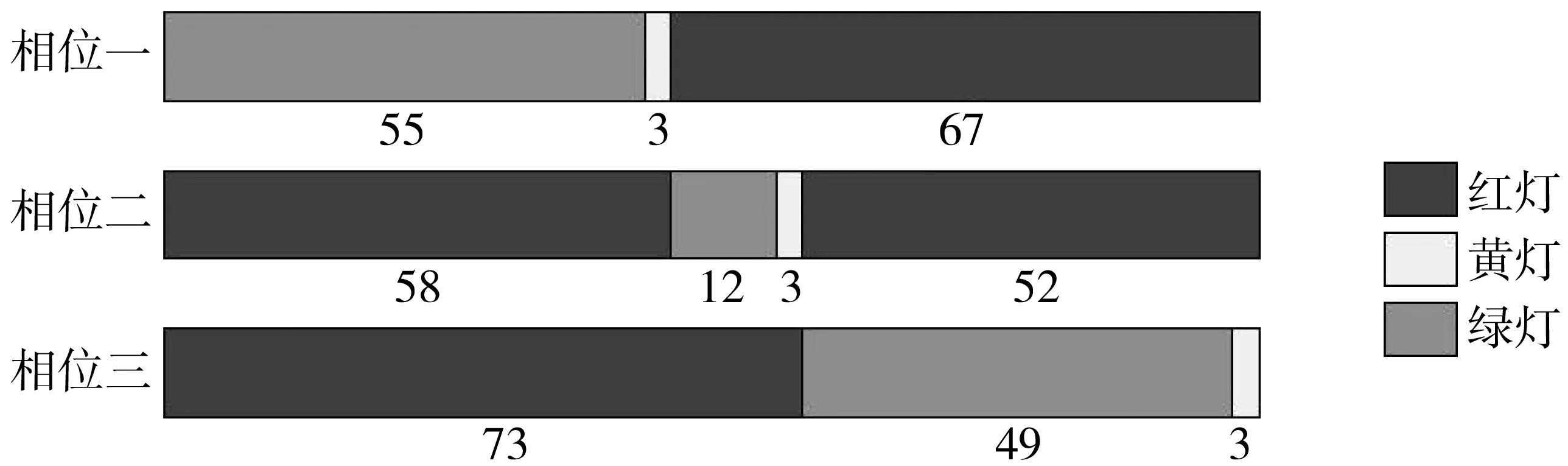
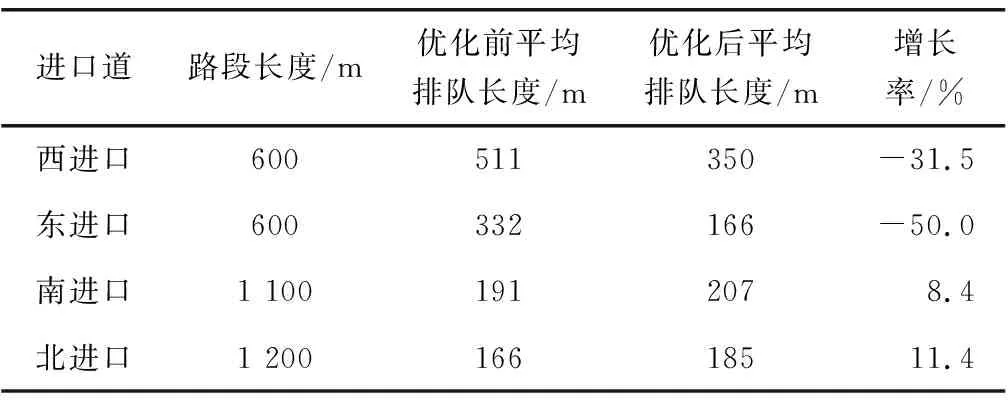
图1表示交叉口进口道红灯时的通行状态,N(r)表示LA段排队等待放行的车辆,此密度近似为阻塞密度kj;N1(r+C)为本周期内进入该路段车辆数,即为LB与LC段即将开始排队的车辆,在LB段车辆开始减速进入队列,LC段车辆正常行驶,此时密度kc介于最佳密度km与阻塞密度kj之间,即km 图1 路段下游产生排队交通流实际运行情况Fig. 1 Actual operation of queued traffic flow downstream ofthe road section N2(r+C)为本周期内离去的车辆数,此时密度kq将由阻塞密度开始减小,故该周期最大车辆排队长度为: (2) 式中:LD为该周期红灯结束时上下游断面间的排队长度,m;kj为上下游断面间的阻塞密度,pcu/m。 当路面状态处于最佳运行状态时,密度为畅行密度km,进口道路段长度为L,此时ΔN(r)=km·L,排队长度LD=0;当路面状态处于阻塞状态时,密度为阻塞密度kj,此时ΔN(r)=kj·L,故排队长度LD=L。因km 1.1.2 多车道模型 当交通流拥挤时,车道变道现象减弱。车流密度越大,空间可压缩性越小,车道间相互影响越小。这时可将多车道视为一个整体,利用交叉口进口单车道红末排队长度模型计算多车道整体排队情况,即: (3) 1.2.1 参数检验 阻塞密度kj是速度为0时的交通流密度。在VISSIM仿真软件中设置3种不同的仿真方案见表1,探讨阻塞密度的取值。仿真结果如图2。 图2 交通密度仿真结果Fig. 2 Traffic density simulation data 表1 仿真方案设置Table 1 Simulation scheme setting 从仿真结果可得,3个方案的阻塞密度kj均在160 pcu/km左右,故取kj=160 pcu/km为仿真与验证模型时的阻塞密度。根据格林柏对数模型如式(4),得到最佳密度km为59 km/h。 (4) 绿灯放行时刻,停车线前后20 m路段的交通密度在90~110 pcu/km之间,kq取均值100 pcu/km。 VISSIM对确定kc位置没有明确方法,提出一种估计方式,由于已知km (5) 1.2.2 仿真方案设置 按照每条车道长500 m、宽3.25 m进行设置,饱和流率为1 800 pcu/h;图3内的上游检测器处安装数量检测器,下游检测器处安置数量检测器和排队计数器,停车线处安置信号灯,单周期60 s,绿灯20 s,红灯37 s,黄灯3 s;仿真时间3 600 s。如图3。 图3 进口道检测器设置方案Fig. 3 Inlet detector setting scheme 连续仿真60个周期,发现从第10个周期开始产生车辆排队,第30个周期开始稳定。为使试验结果更稳定,选择第41到第60个周期作为试验研究对象,模拟排队长度与计算排队长度的当量差在±13 m之间,相对误差均低于±5%。 从相对误差来看,模型计算值与VISSIM模拟排队长度十分接近,使用跟踪误差来描述模型计算值与模拟排队长度之间的偏差,偏差越小意味着模型越可靠,通常认为偏差小于10时,模型可靠。 (6) 式中:Lmi为模型计算的排队长度,m;Lei为模拟试验的排队长度,m;M为周期数。 计算出建立的单双车道模型跟踪误差σ分别为6.78和9.11,因此可认为模型可靠。 路段最大容量是指在现有交通条件下能够容纳的最大车辆数。相邻交叉口之间路段的剩余容量是确定下游交叉口信号控制方案的重要参数之一,通过计算该方向进口道红末排队长度可以得到其剩余道路容量[11]。 2.1.1 道路总容量 取相邻交叉口之间的路段作为研究背景,路段总长度为L,上游交叉口为A,下游交叉口为B,如图4。 图4 研究路段Fig. 4 The section being studied 该路段的总容量为: (7) 2.1.2 排队车辆所占的道路容量 由前文分析可知,路段上车辆排队的长度为L′,那么正在排队的车辆占用路段的容量为: (8) 式中:Q0为排队的车辆占用的道路容量,pcu;L′为路段上已有车辆的排队长度,m。 2.1.3 路段剩余容量 路段上的剩余容量可以通过两个方法计算得到。一是通过总容量和占用容量的差值得到,计算方法见式(9)。 (9) 式中:Qr为路段剩余容量,pcu。 二是通过排队长度计算出未占用路段的长度,该长度所能容纳的车辆数即为路段剩余容量。未占用路段长度为: L″=L-L′ (10) 式中:L″为路段未被占用长度,m。 则剩余容量为: (11) 为避免因次要道路排队溢出而导致的局部路网通行中断,当其排队长度和剩余容量达到一定限值时,应对常规的主路优先控制方案进行调整,降低次路排队长度,减少溢出风险;当排队长度降低到一定程度时,再返回主路优先控制方案,以保证交叉口及其局部路网交通的正常运行。 某相位红灯末期,次路车辆排队达到一定长度,道路剩余容量等于甚至小于下周期内进入交叉口的车辆数,即Qr≤N1时,排队溢出将导致上游交叉口锁死,以此判断控制方案转换的临界值。将式(11)与其联立整理得: (12) 式中:N1为下一周期到达的车辆数,pcu。 将排队长度与道路容量的比值y1作为次路放行的判定条件,即: (13) 式中:y1为容量适配比,m/pcu。 式(12)与式(13)联立,整理得到基于道路剩余容量预测模型的控制方案转换阈值[y1]: (14) 研究对象为四相位固定周期的十字信号交叉口,本节内研究的信号优化方案适用于次要道路处于过饱和状态的交叉口。交叉口车辆排队长度采用1.1节的计算方法,建立主次道路排队长度协调、交叉口延误最小的多目标优化函数,并利用遗传算法求解。 3.2.1 多目标优化遗传算法 多目标优化问题的数学模型为: (15) 式中:Vmin为向量极小化,即向量目标函数f(x)中的子目标函数都尽可能达到极小化。 3.2.2 权重系数法转化 对于多目标优化问题,若给每个子目标函数fi(x)(i=1, 2, …,n)赋予权重ωi(i=1, 2, …,n),其中ωi为对应的fi(x)在多目标优化函数的重要程度,各个子目标函数fi(x)的线性加权和表示为: (16) 若以u作为多目标优化问题的评价函数,则可将多目标优化问题转化为单目标优化问题,即可利用单目标优化遗传算法求解多目标问题。 为降低次要道路的排队长度,充分发挥主路容纳排队的能力,使主、次道路排队长度与其各自容量协调匹配,选取控制交叉口延误、平衡排队长度为优化目标建立函数。 3.3.1 信号交叉口延误模型 交叉口车辆延误是指车辆在交叉口受到信号控制而引起的行程时间损失。研究发现,定数理论适用于车辆到达率大于通行能力的过饱和交叉口的延误评定,计算式为[12-13]: (17) (18) (19) 式中:N为通行能力,pcu/h;q为车流到达率;p为饱和度;d为各车道每车平均延误,s;R为红灯时间,s;y为每小时时平均过饱和滞留车辆数,pcu·h;T为调查持续时间,一般取15 min。 一个周期内交叉口车均延误时间为各进口道延误的加权平均值: (20) 式中:dI为交叉口每车的平均延误,s。 3.3.2 排队均衡策略 排队长度均衡策略是在过饱和交通和主次道路容量差距较大的情况下,为避免某方向(通常是次要道路)排队过长或溢出,分配给排队长度与道路容量之比较大的方向更多绿灯时间,以便及时疏散相应排队车流,防范发生更严重的交通问题[14]。 根据上述思路,单点信号交叉口的控制目标可以简述为: (21) (22) 式中:LE为排队长度均衡性能指标;L′i为各进口道红末排队长度,m;Li为路段长度。 3.3.3 多目标优化模型 目标函数为交叉口车均延误最小,各车道排队长度均衡。利用加权系数法将双目标转化为单目标函数,优化条件及约束条件为: (23) s.t. 式中:α、β为权重系数;dO、LO为优化配时方案交叉口车均延误、排队长度均衡性能指标;dI为原始配时方案交叉口车均延误;LE为排队长度均衡性能指标;C为信号周期,s;gi为有效绿灯时长,s。 以哈尔滨市征仪路与科研街交叉口为例。征仪路为南北方向,双向12车道;科研街为东西方向,双向4车道,为比较典型的容量悬殊的主次道路交叉口,基本情况见表2。信号控制有3个主要相位,相位一为南北直行,相位二为南北左转,相位三为东西直行左转,配时参数如图5。 表2 进口道情况Table 2 The condition of each entrance lane 图5 交叉口配时方案(单位:s)Fig. 5 Timing scheme of intersection 利用摄像法对交通情况进行采集,部分数据如表3。 在交叉口及上游交叉口处设置检测器进行观测并记录经过检测器处的车辆数,计算得到排队长度。表4为多周期数据的平均值。 表4 交叉口排队Table 4 Intersection queuing data 利用式(18)~式(21)计算交叉口各进口道的平均延误以及交叉口的总延误,结果如表5。 表5 交叉口延误Table 5 Intersection delay 通过分析目标交叉口道路交通及控制现状,发现交叉口西进口饱和度最高,因此在计算转换阈值时将西进口作为判断标准。 4.2.1 方案转换判断 取车辆的当量长度l=6 m,前后两车的尾首间距h=2 m,式(13)所涉及排队长度及道路容量的计算参数,根据表4可知西进口道的排队长度L′为511 m,车道数为2条。经计算,容量适配比y1的计算结果为3.4 m/pcu。 下周期内到达车辆数N1的平均值为40 pcu,将各参数代入式(14),计算得到转换阈值[y1]=2.9,y1=3.4>[y1],交通流状态符合方案转换的标准,可以采用笔者提出的控制方法。 4.2.2 权重系数的确定 优化算法求解问题中权重系数α和β的取值通常由主要道路提供的服务水平所决定。当主路服务水平较高时,减小排队长度应该作为主要改善指标,即α<β;当主路服务水平较差时,减小道路延误应作为主要改善指标,而减小排队长度则转移为次要因素,即α>β;服务水平为中等时,α=β。取值范围如表6[6]。 表6 权重系数取值范围Table 6 Value range of weight coefficient 分析征仪路与科研街交叉口,北进口车均延误为34.93 s,相应服务水平为C级;南进口车均延误为35.70 s,相应服务水平为D级。故取值α=0.5,β=0.5。 将采集到的数据输入到优化模型中,利用遗传算法求解,得到优化后的信号配时方案以及该配时方案下的交叉口车均延误和排队长度;对比优化前后的延误、排队长度等数据,以检验模型的适用性和效果。 图6 优化后交叉口配时方案(单位:s)Fig. 6 Timing scheme of intersection after optimization 从表7和表8中可以发现,南北方向主路的排队长度和延误时间略有增加,但东西方向次路的排队长度和延误时间显著降低,交叉口总延误时间与优化前相差不大。图7~图8能够更清楚地显示出协调优化前后各指标的变化情况。 表7 信号配时优化前后延误对比Table 7 Comparison of delay before and after signal timingoptimization 表8 信号配时优化前后排队长度对比Table 8 Comparison of queue length before and aftersignal timing optimization 图7 信号配时优化前后延误对比Fig. 7 Comparison of delay before and after optimization 在原控制方案下,西进口的排队长度接近路段长度,东进口的排队长度接近路段长度的2/3,两个进口道方向均存在排队过长以及溢出的风险。优化后,西进口的排队长度降低到进口道长度的1/2左右,东进口的排队长度降低到进口道长度的1/6左右,大大降低了排队溢出的发生风险;而主要道路在优化前后的排队长度均在路段长度的1/5左右,可以认为优化效果比较均衡,优化方案合理有效。 1)当过饱和交通流持续发展到一定程度时,主次道路容量悬殊的交叉口主要矛盾由保障通行效率转移为避免局部交通阻断和均衡交通需求,控制策略也应相应转变;多参数协调控制方法综合考虑主次道路容量、延误、排队长度、服务水平等,有助于充分利用主路容量以控制次路排队长度、降低排队溢出风险,平衡主次道路的交通需求。 2)实例分析显示,采用多参数协调控制的主次道路交叉口总延误增加了6.44%,主路排队长度增加了8%~11%;但次路延误下降约17%,排队长度下降约30%~50%,表明笔者优化方法在略微增加交叉口总体延误、主路排队长度的同时,较大地降低了次路排队长度和延误,避免排队溢出导致局部路网交通堵塞,控制效果比较均衡合理。
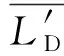
1.2 模型检验
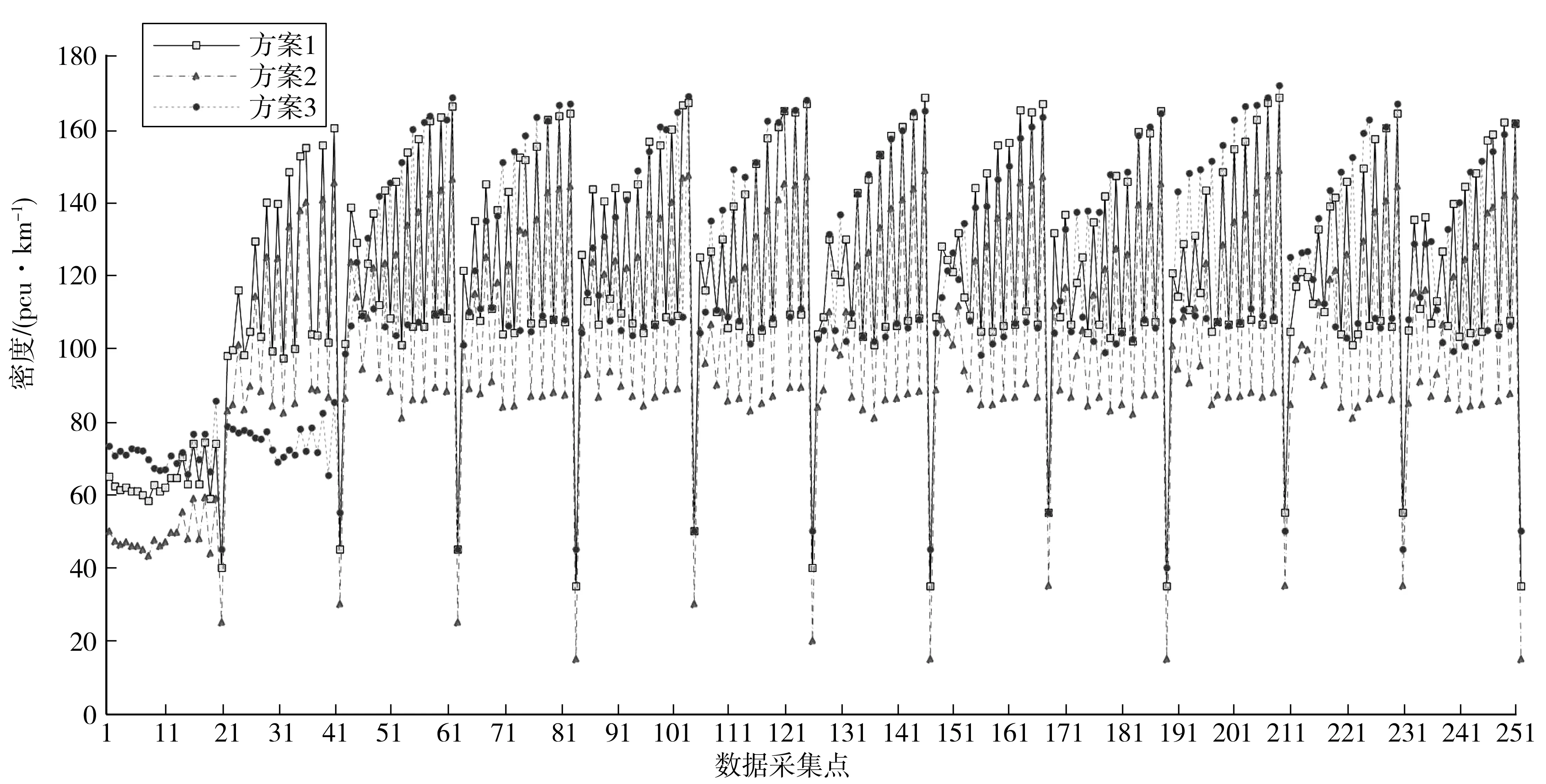

2 信号控制方案转换阈值研究
2.1 路段剩余容量预测模型

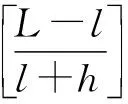
2.2 控制方案转换阈值
3 主次道路多参数协调控制模型
3.1 控制条件
3.2 多目标信号控制优化模型
3.3 优化目标函数及交叉口建模
4 交叉口实例分析
4.1 交叉口道路交通及控制状况
4.2 优化求解

4.3 改进方案对比


5 结 论

