基于纹理特征的PVA纤维束搅拌分散均匀性研究

曹源文，夏 杰，廖 科，曾建民，程志豪

(1. 重庆交通大学 机电与车辆工程学院，重庆 400074； 2. 河南郑州西绕城公路发展有限公司，河南 郑州 450052；3. 云南省交通规划设计研究院，云南 昆明 650299)

0 引 言

聚乙烯醇(PVA)纤维的氢氧碳基团与水泥基的氢氧基团能形成牢固的氢桥[1-4]。在水泥基中加入PVA纤维可有效地增强水泥基的抗裂性能，提高水泥基的寿命[5-8]。然而，PVA纤维是束状形式的微米级材料，在水泥基中难以分散均匀，导致PVA纤维的优良性能在公路交通建设中难以显现[9]。

笔者在水泥基中加入PVA纤维之前，对PVA纤维进行搅拌分散，以此达到在水泥基中提高PVA纤维的分散效果，增强水泥基强度。PVA纤维的束分散均匀性是将PVA纤维束状形态分散为单丝网状形态的程度。纤维分散效果评价方法对研究纤维分散均匀性是最重要的一部分。能快速、准确地评价PVA纤维束在水泥基中的分散效果对于实际工程中提高PVA纤维束分散均匀性具有较大参考和借鉴价值。

传统纤维束分散评价一般是通过直接观察纤维束的分散情况进行。景元琳[10]使用透明容器装纤维混合液，直接观察纤维束的分散情况；白光等[11]通过对实验得到的混凝土性能进行测试，得到PVA纤维束对水泥基的强度影响情况；仇何等[12]根据测量分散后的分散系数等相关参数对分散效果进行评价。笔者利用数字图像处理技术，采集PVA纤维束分散统计型纹理特征信息，采用灰度共生矩阵理论，分析评价了PVA纤维束和粉煤灰质量比、搅拌转速及搅拌时间对PVA纤维束分散均匀性的影响，得到了最佳质量比、最佳转速和搅拌时间。

1 统计型纹理特征

纹理是反映图像中不受颜色、亮度变化影响的同质现象的视觉特征。纹理特征可表示图像的灰度等级分布，纹理特征基本元素为：① 纹理基元，由像素组成具有一定色调、大小、形状和区域属性的连续集单元；② 纹理基元排列组合，通过纹理基元进行排列组合形成纹理。

统计型纹理特征能很好地表示图像纹理的分布均匀性情况[13]。统计型纹理分析是指从区域统计方面来进行图像纹理分析，通过图像灰度空间分布情况对图像纹理的粗细度、均匀性、方向性进行描述。笔者研究的是PVA纤维束分散后图像，图像中PVA纤维与混合物质的灰度值差异大，故统计型纹理特征能很好表示PVA纤维束的分散均匀性。

2 统计型纹理特征评价方法

统计型纹理特征根据像素及周围的灰度信息，研究区域内的灰度统计特征。统计型纹理特征参数用灰度共生矩阵特征参数表达，灰度共生矩阵表示在某个方向上相隔d个像素的一对像元的灰度值分别是i和j的概率，这是计算估计图像的二阶组合条件概率密度方法，能很好表示图像纹理的分布均匀性情况。

2.1 灰度共生矩阵理论

定义灰度等级为e1的点为原点，某像素点距离此点(Δx, Δy)的灰度等级为e2，坐标关系如图1。

图1 灰度共生矩阵点对的位置关系Fig. 1 The positional relationship of the point pairs of the graylevel co-occurrence matrix

(Δx, Δy)取不同值时，在不同方向上就可得到像素点对的灰度共生矩阵P(e1,e2,d,θ)，如式(1)：

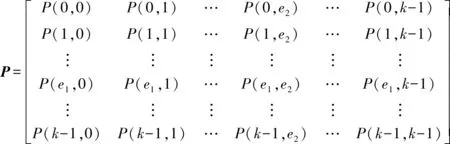
(1)

(2)

式中：d为灰度共生矩阵的生成步长；θ为灰度共生矩阵的生成方向；N为灰度共生矩阵元素总数。

2.2 统计型纹理特征参数选取

灰度共生矩阵有很多的特征参数，其中，R.M.HARALICK[14]定义了14个特征参数来描述纹理特征。这14个参数中角二阶矩反应了图像分布均匀性，熵值反应了图像纹理粗细和复杂程度。笔者选用角二阶矩和熵值这两个参数来进行PVA纤维分散的均匀性评价。

1)角二阶矩计算如式(3)：

(3)

从式(3)中可看出：在图像中纹理越粗，角二阶矩f1的值更大，灰度分布更不均匀；相反，纹理越细，角二阶矩f1值更小，灰度分布更均匀。

2)熵值f2(entropy)的计算如式(4)：

(4)

当图像中没有纹理时，矩阵P为零矩阵，熵值f2趋近零；当图像中充满了大量纹理，矩阵P(e1,e2,d,θ)中的数值几乎相似，此时熵值f2最大；当图像中有较少纹理时，矩阵P(e1,e2,d,θ)中元素数值差异较大，熵值f2较小。

2.3 图像统计型纹理特征参数提取

PVA纤维通过分散试验之后，对分散后的试验样品进行图像提取，得到分散纤维的RGB图像，利用MATLAB的图像格式转换程序将RGB彩色图像转化成灰度图像。将灰度图像利用灰度共生矩阵程序在MATLAB中计算，得到分散纤维角二阶矩和熵值两个特征参数[15]。采集流程如下：

1)将灰度图像进行等级压缩，将256级压缩到16级；

2)取d=1，θ=0°、45°、90°、135°，在不同方向下计算出4个灰度共生矩阵；

3)将矩阵归一化处理；

4)按照式(3)、式(4)，得到灰度图像角二阶矩和熵值；

5)在0°、45°、90°、135°这4个方向上进行计算，得到角二阶矩和熵值，并对其进行平均化，得到统计型纹理特征参数。

2.4 PVA纤维束搅拌分散均匀性评价

笔者提取试验后的PVA纤维图像统计型纹理特征，用灰度共生矩阵中的角二阶矩与熵值表示，用此特征参数来进行均匀性评价。在PVA纤维理想状态的图像中，图像纹理越大，灰度分布越不均匀，角二阶矩越大；图像纹理越小，灰度分布越均匀，则角二阶矩就越小。若灰度共生矩阵中数值都相同，则图像熵值最大，纹理分布最复杂；若灰度共生矩阵中数值差异很大，则图像熵值越小，纹理分布复杂程度越低。

因此，对分散后的PVA纤维束提取样本，其角二阶矩越小、熵值越大，即呈现单丝网状结构图像纹理越细小、分布越复杂，则PVA纤维分散均匀性效果越好。

3 PVA纤维束搅拌分散试验及分析

3.1 搅拌分散装置设计和材料选取

使用双轴双电机搅拌设备对PVA纤维束进行分散处理。搅拌装置包括电机控制器、两个电动机、两个搅拌轴、联轴器、搅拌叶片、搅拌槽，使用联轴器将两个电机的输出轴分别和两个搅拌轴连接。

将粉煤灰和PVA纤维束混合进行搅拌分散试验。粉煤灰等级为二级，细度为43 μm，密度为2.4 g/cm3，含水量为0.5%；PVA纤维束长度为18 mm。图2(a)为粉煤灰，图2(b)为PVA纤维束。

图2 粉煤灰和PVA纤维束Fig. 2 Fly ash and PVA fiber bundle

3.2 不同质量比对PVA纤维束分散效果试验分析

在研究不同质量比对PVA纤维束分散效果影响时，选用4组不同的PVA纤维和粉煤灰比值，分别为：1∶15、1∶30、1∶45、1∶60。电机转速为700 r/min，对纤维和粉煤灰搅拌时间为2 min。为保证试验的准确性和防止设备、操作等误差影响，每种质量比进行5次搅拌分散试验，然后提取每次的角二阶矩和熵值两个纹理特征参数，并对5次试验特征参数求平均值。图3为试验后不同质量比下的PVA纤维与粉煤灰混合示意。

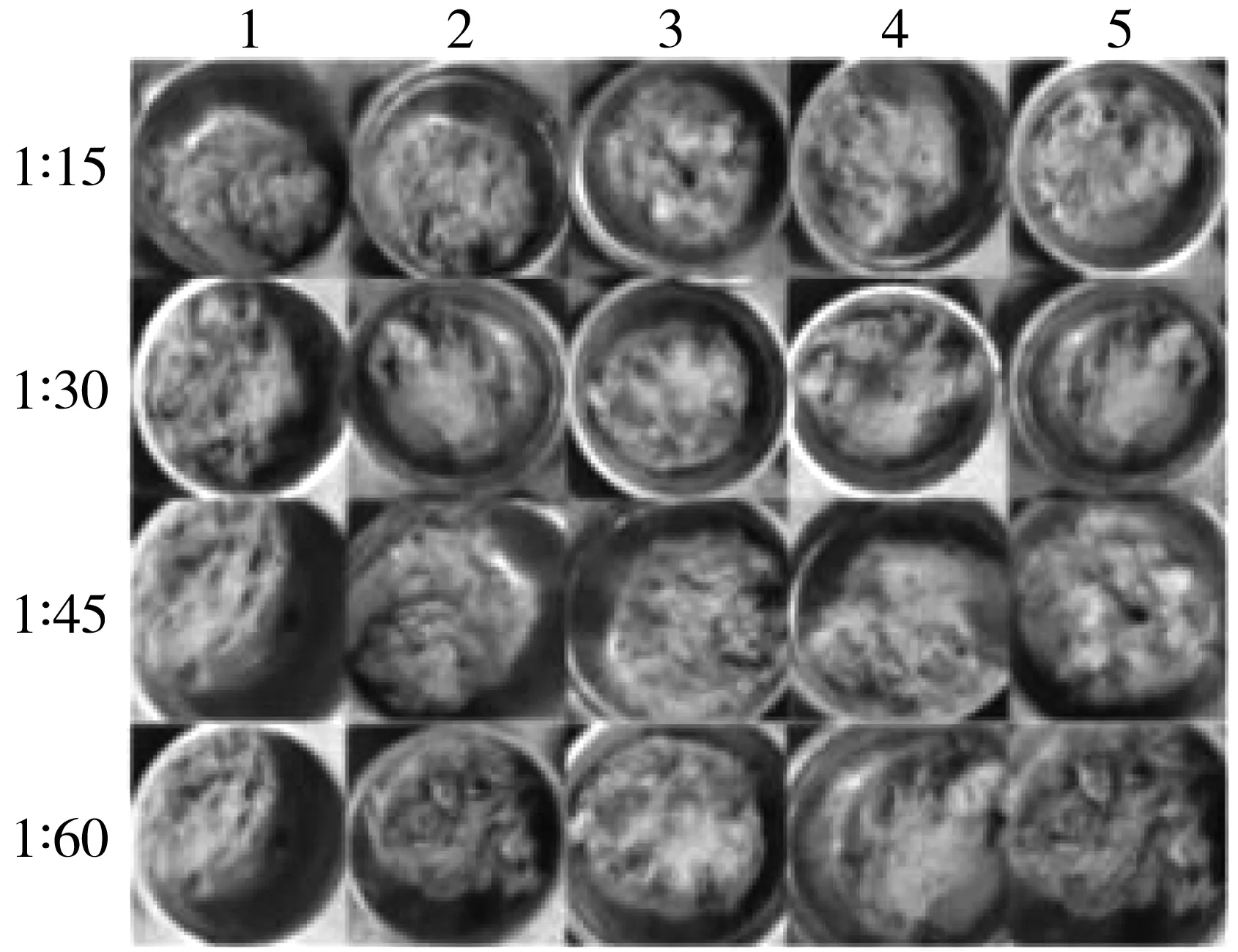
图3 不同质量比下分散后的PVA纤维Fig. 3 PVA fiber dispersed at different mass ratios

搅拌分散试验后，使用料筛将粉煤灰筛去，用水洗去PVA纤维上剩余的粉煤灰，图4为水洗后的PVA纤维。

图4 水洗后PVA纤维Fig. 4 PVA fiber after washing

采集水洗后的PVA纤维图像，提取经处理后的图像统计纹理特征参数，得到每次试验的PVA纤维角二阶矩与熵值；然后对每组质量比下得到的角二阶矩与熵值求其平均值，将特征参数平均值作为评价PVA纤维束分散效果参数。

利用得到的PVA纤维角二阶矩和熵值平均值绘制角二阶矩随质量比变化曲线和熵值随质量比变化曲线，如图5。

图5 角二阶矩和熵值分别与质量比关系曲线Fig. 5 Relationship curve between angular second-order moment, entropy and mass ratio respectively

从图5可看出：PVA纤维中加入一定的粉煤灰，对PVA纤维束分散起着促进作用。图5(a)中：随着加入粉煤灰比例增加，分散后的PVA纤维图像角二阶矩越小，分散质量越好，当纤维束和粉煤灰比值增加到1∶45之后，图像角二阶矩变化不明显，对提升纤维束分散质量不明显。图5(b)中：随着加入粉煤灰比例增加，分散后的PVA纤维图像熵值更大，分散质量越好，当纤维束和粉煤灰比值增加到1∶45之后，熵值变化很小，对于提升纤维束的分散质量影响不大。

3.3 不同转速对PVA纤维分散效果试验分析

在转速对PVA纤维分散质量的影响试验中，纤维束和粉煤灰质量比为1∶45时进行试验。当转速为300～900 r/min时，进行了7种转速工况的试验，每种转速工况相差100 r/min，搅拌时间为2 min，每组试验使用5 g PVA纤维。

试验得到不同转速下搅拌分散后PVA纤维的角二阶矩和熵值平均值，并绘制角二阶矩随转速变化曲线和熵值随着转速变化曲线，如图6。

由图6可看出：提高装置转速，对PVA纤维束分散起着促进作用。图6(a)中：随着转速增加，分散后的PVA纤维图像角二阶矩越小，分散质量越好，随着转速达到700 r/min后，图像角二阶矩变化不明显，对提升纤维束分散质量不明显。图6(b)中：随着转速增加，分散后的PVA纤维图像熵值更大，分散质量越好，当转速达到700 r/min后，熵值变化很小，对提升纤维束分散质量影响很小。

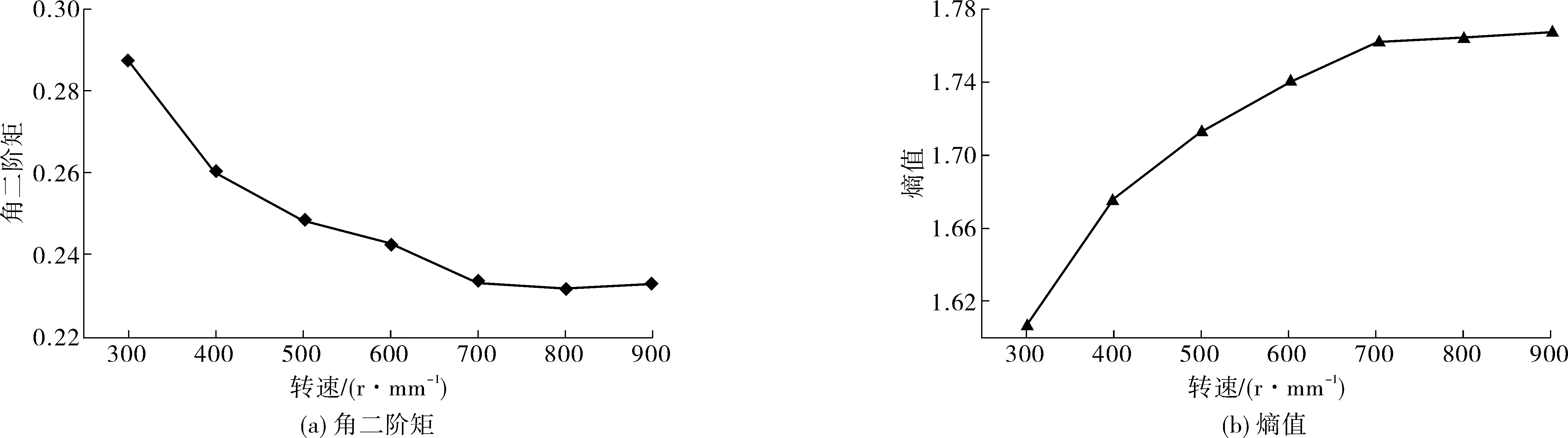
图6 角二阶矩和熵值分别与转速关系曲线Fig. 6 Relationship curve between angular second-order moment, entropy and speed respectively

3.4 不同搅拌时间对PVA纤维分散效果试验分析

在搅拌时间对PVA纤维分散质量影响试验中，纤维束和粉煤灰质量比为1∶45，转速为700 r/min时进行试验。搅拌时间为2～4 min，进行了5种不同搅拌时间试验，每次搅拌时间相隔0.5 min，每组试验使用5 gPVA纤维。

试验得到不同搅拌时间下的PVA纤维角二阶矩与熵值平均值，绘制角二阶矩随搅拌时间变化曲线和熵值随着搅拌时间变化曲线，如图7。

从图7可看出：增加试验搅拌时间，对PVA纤维束分散起着促进作用。图7(a)中：随着搅拌时间增加，分散后的PVA纤维图像角二阶矩越小，分散质量越好，随着搅拌时间增加到3 min后，图像角二阶矩变化不明显，说明继续增加搅拌时间对提升纤维束分散质量不明显。图7(b)中：随着搅拌时间增加，分散后的PVA纤维图像熵值更大，分散质量越好，当搅拌时间达到3 min后，熵值变化很小，甚至有下降趋势，对提升纤维束分散质量影响不大。

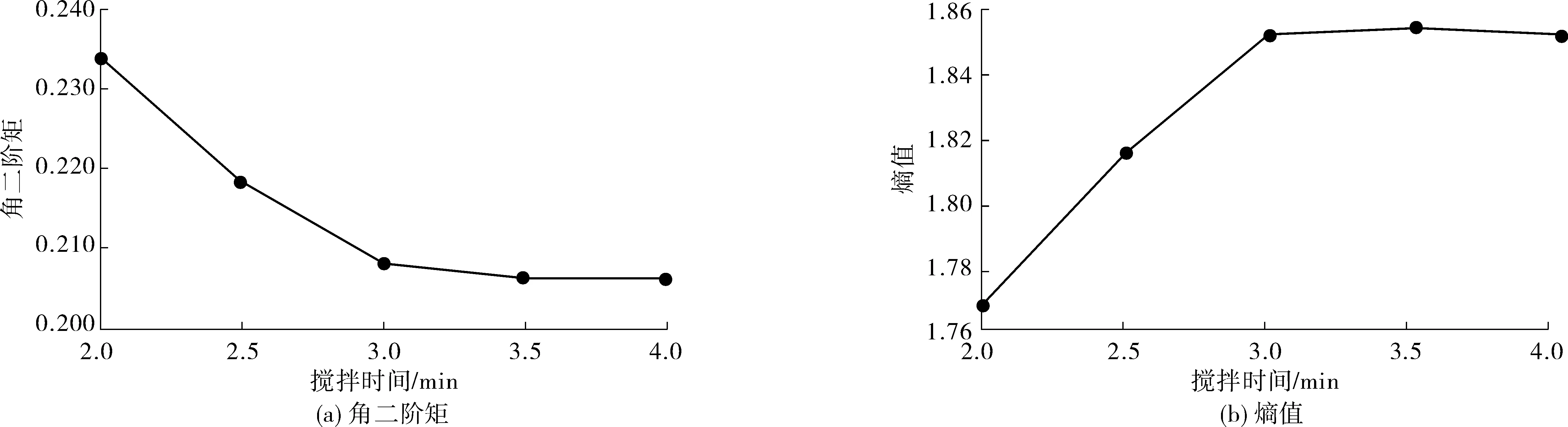
图7 角二阶矩和熵值分别与搅拌时间关系曲线Fig. 7 Relationship curve between angular second-order moment, entropy and stirring time respectively

4 结 论

1)笔者采用数字图像纹理处理技术，对搅拌分散试验后的PVA纤维束提取图像进行处理，利用灰度共生矩阵理论提取图像的统计型纹理特征参数：角二阶矩和熵值，以此表征图像纹理均匀性分布情况，实现对搅拌分散后的PVA纤维束进行均匀性评价。该方法能快速、准确地评价纤维束搅拌分散均匀性情况。

2)笔者开展了在不同PVA纤维束与粉煤灰质量比、不同转速和不同搅拌时间下的PVA纤维束搅拌分散试验。结果表明：粉煤灰加入比例越高，分散效果越好，但PVA纤维和粉煤灰质量比达到1∶45后，继续添加粉煤灰，改善分散效果不明显；提高转速，能改善PVA纤维分散效果，但转速达到700 r/min后，继续提升转速，对分散效果没有促进作用，甚至降低PVA纤维束分散效果；增加搅拌时间，能改善PVA纤维分散效果，但搅拌时间在3 min后，增加搅拌时长对PVA纤维分散效果提升不大。试验表明：最佳质量比为1∶45，最合适转速为700 r/min，最佳搅拌时间为3 min。