无人飞行器协同探测构型方法研究

丁力全,刘亚飞,吴 楠,白显宗

(1. 战略支援部队信息工程大学数据与目标工程学院,河南 郑州 450000;2. 战略支援部队兴城特勤疗养中心，辽宁 兴城 125105； 3. 中国人民解放军66132部队,北京 100042; 4. 军事科学院国防科技创新研究院,北京 100000)

通过运用飞行器如助推滑翔飞行器、导弹、卫星等进行协同作战,可以实现通信共享,有效躲避敌方的识别和侦察,同时又可以实时同步地对目标进行侦察、跟踪、决策和打击,突防能力相比单飞行器作战有飞跃式的提升。协同探测是协同作战领域的重要环节,协同探测技术是指利用多平台上的传感器的量测数据进行信息的融合,使用融合后的数据对观测目标进行定位与跟踪,该技术能够综合利用全面、多维度的信息得到比单传感器更加准确、可靠的定位与跟踪结果。飞行器协同探测可以更好地扩大探测范围,进一步提升跟踪定位精度。协同探测在经济成本、可操作性、便捷性、实时性等方面具有一定的优势,是协同作战领域中不可或缺的一环。

当前,常用的定位手段有雷达探测、红外观测等方法。对于雷达探测,现有的研究大多集中于地面、海面静止或移动传感器跟踪定位目标。对于红外传感器,常用的手段是卫星定位。在国内外公开文献中,多是对机载、无人机载协同探测原理进行研究。而飞行器在空间中具有速度快、飞行距离远、容易躲避攻击等优势,因此协同作战在空间战场上的应用价值更高,具有重大的研究意义。

衡量定位精度需要用一定的参数指标作为参考,目前,有以下几种方法可以评价定位精度:几何精度稀释(GDOP)、克拉美罗下界(Cramer—Rao Lower Bound,CRLB)、椭圆误差概率(Circular Error Probable,CEP)等。其中GDOP本质上可以看作最小二乘估计,而CRLB是最大似然估计,当系统为线性系统且噪声为高斯独立白噪声情况下,两者等价,但非线性系统中,两者不同。这是由于,GDOP忽略了误差协方差对角线元素,对传感器几何位置敏感性要高于CRLB,是用作传感器目标几何不确定性的分析工具,而CRLB用作基于源自目标的传感器观测值的统计性能评估工具。

因此,本文将同时运用不同组合的雷达与红外传感器对地面目标进行探测,通过数据处理,利用GDOP对不同场景的探测构型进行分析对比,同时兼顾飞行器成本,给出了一种最佳的探测构型。

1 目标模型建立及GDOP求解

1.1 目标模型的建立

考虑观测目标为地面静止目标,然后可以确定目标的状态方程如下:

状态矢量设为目标在地固系中的位置矢量

(1)

由于为静止目标,状态方程为

+1=

(2)

即状态转移矩阵为三阶单位阵。

1)对于红外传感器,测量量只有俯仰、方位角两个数据,即需要建立观测矢量(,)与状态矢量的函数关系。假设飞行器在地固系中的位置矢量为

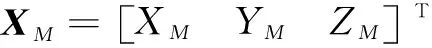
(3)

飞行器与目标之间的视线矢量在地固系中可表示为

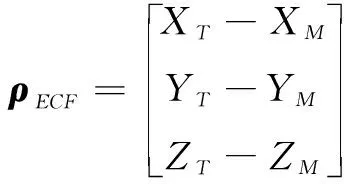
(4)

将地固系下的视线矢量转换到地心惯性(视场)坐标系中,可表示为

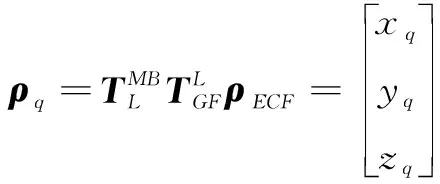
(5)

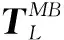
利用视场坐标系中的视线矢量计算观测矢量:

(6)

2)雷达的测量量包括俯仰角、方位角和距离,观测矢量:

(7)

1.2 GDOP求解

以雷达为例,设其在地固系下的位置为(,,),第个雷达观测的距离、方位、俯仰角分别为、、,可表示如下:

(8)

令=(,,,,,),=(,,,,,),=(,,,,,),对上式取微分可得:

(9)

相比于卫星、雷达和机载传感器,飞行器由于其运动非线性较强,一阶导数很难用计算得到。在此,利用雅克比矩阵对一阶偏导数进行求解,可得到较为精确的数值。

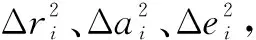
令

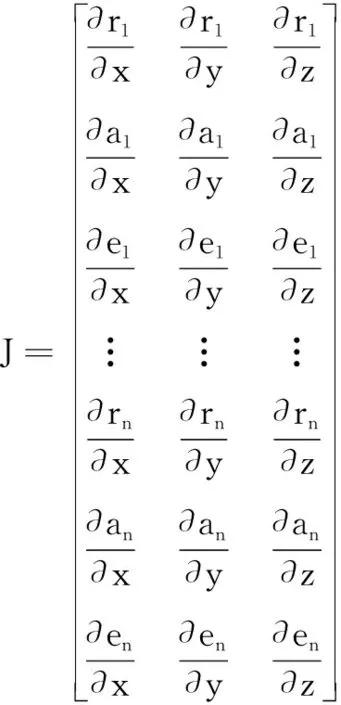
(10)

由极大似然准则,融合后误差协方差矩阵和定位精度GDOP可表示为:

=()

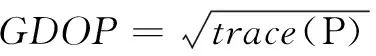
(11)

红外传感器与雷达原理相同,只是缺少距离测量量,在此不再赘述。本文使用的信息融合方法选用集中式融合,详细步骤见文献[19]。

1.3 构型影响因素分析

为了便于仿真分析,对模型适当简化,此时可以构建误差分析解析模型,在一定程度上能够反映问题的本质机理,即使模型后续进一步复杂,也不会影响或者推翻本质结论。

以双视线定位构型对精度的影响分析为例。对该问题进行简化抽象,三点可以确定一个平面,相对位置如图1所示。

图1 双视线定位构型示意图

图中为目标位置,1和2分别为两个飞行器的位置,假设角度、、为未知量，为已知量,或为待求量,求出任何一个就可以完成目标定位。根据图中几何关系,可知

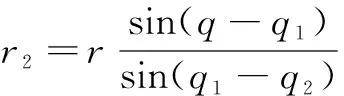
(12)

式中，假设、是精确已知的,、有测量误差,分别求关于、的偏导数：

(13)

(14)

偏导数相当于误差传播系数,数值越大,则测量误差导致的定位误差就越显著,因此需要偏导数数值尽量要小,基于这个原则,可以看出:

1)当两个视线角相等时,即两个传感器和目标在一条直线上,偏导数的分母趋近于0,定位效果相对较差;

2)文献[20]详细描述了两部传感器与目标之间的角度与GDOP数值的关系,在本文中,引用该理论,可以得出结论:当存在=90°-2-2时,计算偏导数为最小,可以使GDOP值达到最小,定位精度最高,此时目标与两部传感器之间的位置关系为等腰三角形,定位效果最好;

3)当视线角的差一定时,越大，偏导数越大,定位效果越差,即飞行器离目标距离越远，定位效果越差。

4)随着传感器数量的增加,则需要每两个传感器和目标之间保持等腰三角形的位置关系。当三个传感器时,传感器之间几何关系为正三角形,以此类推,从而使偏导数达到最小值,提升定位精度。

2 仿真及分析

2.1 仿真场景

2.2 已知先验信息和原则

1)所有飞行器的发射区域和飞行空间区域是有限且确定的,构型和路径设计均应包含在此区域内;且多传感器发射高度假定相同(即在同一水平面内发射)；

2)不考虑信号级的影响,纯从空间几何角度考虑,可测距的雷达导引头探测性能不受相对构型影响,因为单传感器即可完成定位,定位模型与其他传感器并没有交联;

3)从空间几何角度考虑,受地球曲率影响,飞行高度越高,对目标的可观测弧段越长,发现目标越早,但飞行高度还应受动力学和突防要求约束;

4)当测角精度一定时,传感器距离地面目标越近,定位系统精度越高,但飞行器与目标距离还应受动力学和突防要求约束;

5)对于仅测角的红外导引头,由于单个传感器无法对目标进行立体定位,需要多个传感器协同定位,因此定位精度与传感器构型关系密切,需重点研究;

6)红外导引头由于是被动探测,突防性能优于雷达导引头,但不能测距,两者各有优劣;

7)在满足定位精度需求条件下,飞行器数量尽量少,雷达导引头数量尽量少。

2.3 雷达传感器构型仿真分析

1)飞行器不同间距情况下的GDOP。假设飞行器发射位置在一条直线上,间距离分别设为1 km、2 km和3 km,雷达测量的俯仰角和方位角误差均为0.1°,测距误差设置为100 m。分别对比1～10个雷达在不同间距下的GDOP数值,仿真结果见图2。

图2 雷达在不同间距下的GDOP对比图

由图2可以看出,对于雷达传感器而言,相邻两个雷达站间距2 km相比于雷达间距1 km的精度提升3.04%,间距3 km相比于间距2 km的精度提升4.1%,间距3 km相比于间距1 km的精度提升7.1%,在发射半径一定的条件下,雷达站间距越大,GDOP值越低,定位精度越高。从图形斜率可以看出,雷达间距1～3 km的GDOP及各方向的精度变化规律相同,在雷达站数量为1～5部时,斜率较大,精度提升较快;在5～10部时,斜率较低,精度变化相对平缓。通过分析GDOP值,可以得出:雷达站间距1 km～3 km时,1～5部雷达的精度变化率分别可以达到56.1%、58.1%、60.5%,5～10部雷达精度变化率分别只有30.8%、33.8%、35.8%。

2)几何位置对定位精度的影响。假设飞行器发射位置在同一平面内,构成不同的几何形状。参数设置与(1)相同。由上述分析可知,5个以上飞行器协同探测的精度变化较为平稳,因此只分析3～5部雷达在不同几何位置关系下的GDOP,见表1～表3。

表1 三部雷达不同位置下的GDOP

表2 四部雷达不同位置下的GDOP

表3 五部雷达不同位置下的GDOP

对于雷达而言,在边长一定的情况下,正多边形布站构型的精度相对其余构型虽然在各方向上的精度略有差异,但整体GDOP值最小。就整体数值而言,雷达传感器由于能够观测到目标与传感器间的距离,因此传感器构型对定位精度影响不大。

3)不同发射时刻情况下的GDOP。令发射点与的连线和轴共面,点在轴所构成的平面外,分别讨论正三角形与平面夹角为90°、60°、45°、30°四种情况(飞行器在不同平面内同时发射,与在同一平面内发射时刻不同的场景等效)。仿真结果见表4～表6。

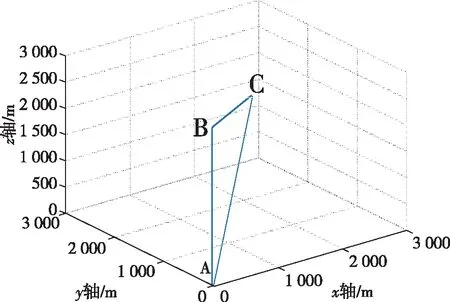
图3 飞行器发射位置关系

表4 三部正三角形构型条件下雷达不同发射角度(时刻)的GDOP

表5 四部正方形构型条件下雷达不同发射角度(时刻)的GDOP

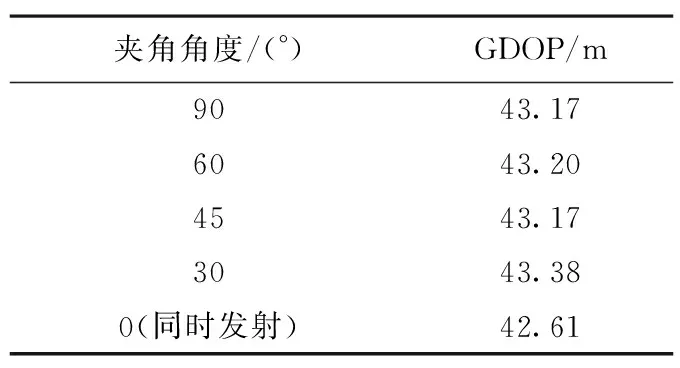
表6 五部正五边形构型条件下雷达不同发射角度(时刻)的GDOP

由仿真结果可以看出,雷达进行多站协同探测,当构型相同时,满足同时发射(轴位为多点发射面的法线)才能保证精度最高。

4)全轨道定位GDOP分析。考虑全轨道定位的效果,以间距为3 km的正三角形、正方形和正五边形布站类型作为仿真条件,对全轨道定位GDOP进行分析。对于雷达俯仰、方位角误差分别设为0.1°、0.1°,测量距离误差为100 m,仿真结果见图4。

图4 雷达全轨道定位GDOP

根据仿真结果,传感器在接近目标的过程中,随着与目标的距离减小,测量精度也不断提升。由于飞行器具有相同的初始飞行条件,因此在飞行过程中构型位置变化可近似看作不改变,因此,仍然满足传感器越多,精度越高的这一结论。

2.4 红外传感器构型仿真分析

1)飞行器不同间距情况下的GDOP。假设飞行器发射位置在一条直线上,间距离分别设为1 km、2 km和3 km,红外测量的俯仰角和方位角误差均为0.1°，分别对比2～10个红外在不同间距下的GDOP数值,仿真结果见图5(由于单部红外传感器只有1组俯仰角和方位角数据,无法进行精确定位,故在此不进行对比)。

图5 红外在不同间距下的GDOP对比图

对于红外传感器,相邻两个飞行器间距2 km时相比于间距1 km的精度提升49.3%,间距3 km相比于间距2 km的精度提升30.4%,间距3 km相比于间距1 km的精度提升64.7%,与雷达传感器相同,在发射半径一定的条件下,随着红外传感器间距增大,GDOP数值减小,定位精度不断提升。而且在传感器距离变化相同的情况下,随着距离的增加,红外传感器要比雷达传感器精度提升更明显。从图形斜率可以看出,红外传感器间距1～3 km的GDOP及各方向的精度变化规律也是相同的,在传感器数量为2～5部时,斜率较大,精度提升较快;在5～10部时,斜率较低,精度变化相对平缓。通过分析GDOP值,可以得出:红外传感器间距1 km～3 km时,2～5部传感器精度变化率分别可以达到71.2%、71.5%、71.4%,5～10部传感器精度变化率分别只有53.2%、52.1%、49.6%。

2)几何位置对定位精度的影响。假设多传感器发射位置在同一平面内,构成不同的平面图形。红外传感器测量的俯仰角和方位角误差均为0.1°,分析3～5部红外传感器在不同几何位置关系下的GDOP,见表7～表9。

表7 三部红外不同位置下的GDOP

表8 四部红外不同位置下的GDOP

表9 五部红外不同位置下的GDOP

红外传感器相比雷达传感器,在测量误差相同的情况下,由于没有观测距离,因此构型的设计影响观测的角度,所以构型不同对于精度影响较大。对于三站传感器,等边三角形布站精度相比于直角三角形提升14.4%,相对于三点共线提升30.5%。对于四站传感器,正方形布站精度相比于平行四边形提升7.4%,相比于四站共线提升47.7%。对于五站传感器,正五边形布站相比于任意五边形提升24.8%,相比于五点贡献提升37.6%。因此,选用红外传感器进行观测时,应选用正多边形布站类型,能使定位精度得到有效的提升。

3)不同发射时刻情况下的GDOP。仿真设置与2.3节中第(3)部分相同。结果见表10～表12。

表10 三部正三角形构型条件下红外不同发射角度(时刻)的GDOP

表11 四部正方形构型条件下红外不同发射角度(时刻)的GDOP

表12 五部正五边形构型条件下红外不同发射角度(时刻)的GDOP

由仿真结果可以看出,红外传感器同样满足同时发射,才能保证精度最高,而且其精度提升相比于雷达传感器更为明显。

4)全轨道定位GDOP分析。与雷达全轨道定位精度分析类似,红外俯仰、方位角误差均设为0.1°、0.1°,仿真结果见图6。

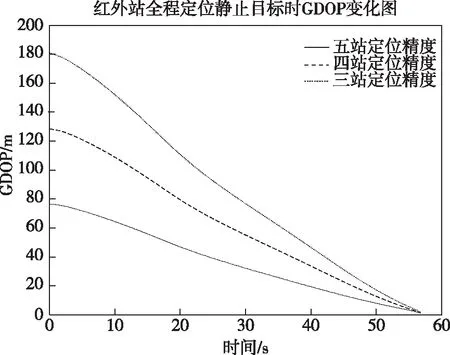
图6 红外全轨道跟踪下的GDOP

根据仿真结果,红外定位仍然满足观测站越多,精度越高的这一结论。

2.5 组合测量仿真分析

由于雷达与红外传感器有各自的观测精度和造价成本,因此,需要选择性价比最高的组合测量方式,既能满足观测精度,又能减少成本,使费用与精度达到最优比,能够更好地应用于工程实际。

假设一部雷达的成本为50万元,一部红外传感器的成本为10万元,导引头雷达与红外的测量俯仰角和方位角误差均为0.2°,雷达的距离测量误差为0.3 m。布站类型均采用正多边形布站,传感器间的距离均设为3 km,成本和观测精度所占权重分别为0.5,下述精度最高与精度最低的GDOP取值区间为[1.432 923 95,51.395 288],费用最高与费用最低的取值区间为[2,25],归一化参数可表示为

归一化参数=[(GDOP-1.432 923 95)/(51.395 288-1.432 923 95)]*0.5+[(PRICE-2)/(25-2)]*0.5

按不同方式组合测量结果见表13。

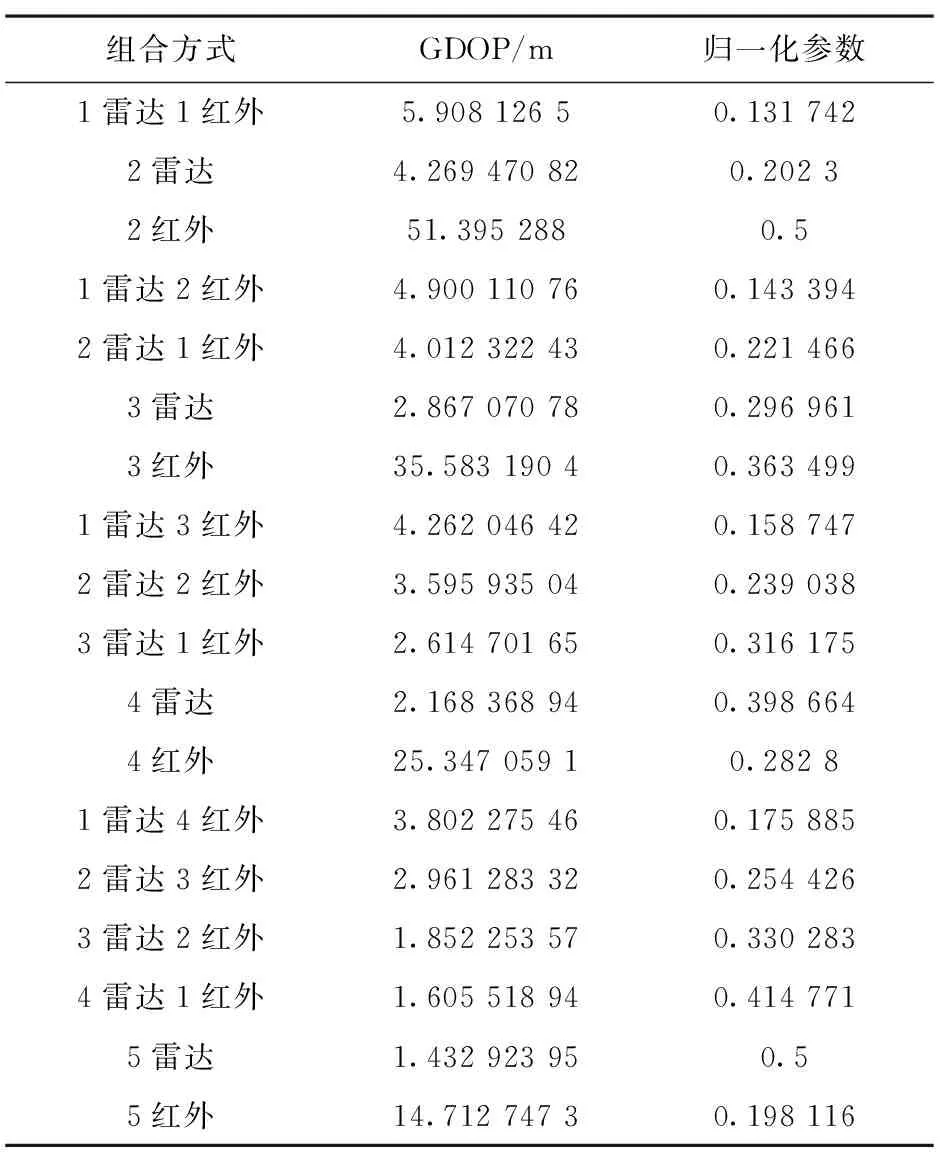
表13 不同组合测量方式下的归一化参数

由上表可知,按照上述归一化参数计算条件,1部雷达和1部红外传感器进行组合测量时,归一化参数最低。在实际应用中,应按照实际需求,对归一化参数进行计算,以此来选择最合适的组合方式进行测量。

3 结束语

本文利用GDOP指标,通过改变飞行器之间的距离、飞行器的位置、飞行器的发射时刻等条件,验证了协同探测精度的影响因素。本文首先分析了影响探测精度的因素,在飞行器间距方面,雷达和红外传感器,在发射半径一定的条件下,站间距增大,GDOP值减小,定位精度不断提升。在飞行器位置方面,正多边形布站方式可以实现定位精度最高。其中,红外传感器的观测精度受构型的影响较大。在发射时刻方面,当飞行器同时发射时,定位精度最高。其次,证明了在飞行器从发射到打击目标的全过程中,随着飞行器与目标之间的距离减小,GDOP值也不断减小,定位精度不断提升,且在全轨道的定位过程中也能较好地满足定位精度要求。最后,结合探测精度和传感器成本因素,提出一种最优参数设计方案,当给定定位精度和价格的权重时,依据此方案能够计算出最优参数,以便选择最佳的传感器数量和最佳探测构型。