初中学生数学原理学习状况的调查研究

张青云

摘  要：初中数学深度学习是对数学知识本质的理解，是对知识内在联系的认识和整体把握. 在数学原理的学习过程中，调查数据显示，当前初中学生对运算法则的理解程度不高，对数学对象的性质、定理的推导与证明水平不高，对初中数学知识的整体结构和内在联系的理解和掌握不够理想. 提出三项教学建议，即以SOLO分类评价构建数学原理学习的目标层级，加强数学原理学习的过程教学，加强数学原理关联知识结构的整体教学，并提出了数学原理学习的实施路径.

关键词：数学原理;深度学习;SOLO分类

一、问题提出

根据深度学习教学改进项目组对深度学习的界定，在由刘晓玫主编的《深度学习：走向核心素养（学科教学指南·初中数学）》一书中，对初中数学深度学习的内涵做了这样的界定：初中数学深度学习就是在教师引领下，学生围绕具有挑战性的数学学习主题，全身心地积极参与、体验成功、获得发展的有意义的数学学习过程. 在这个过程中，学生开展以从具体到抽象、运算与推理、几何直观、数据分析和问题解决等为重点的思维活动，获得数学核心知识，把握数学的本质和思想方法，提高思维能力，发展数學学科核心素养，形成积极的情感、态度和正确的价值观，逐步成为既具有独立性、批判性、创造性，又具有合作精神的学习者. 在数学知识分类中，通常把公理、定理、法则、公式、数学对象的性质等统称为数学原理. 初中数学原理学习是初中数学课程内容的核心之一，也是初中数学深度学习的重要主题材料. 在当下的初中数学学习过程中，我们的学生对初中数学原理学习的效果到底如何？是否体现了初中数学深度学习的发生？为此，我们展开了一项针对初中学生数学原理学习状况的调查研究.

二、研究方法

1. 调查目的

了解初中学生对初中数学课程中常见的三类数学原理（即法则、性质、定理）的理解和掌握水平.

2. 调查方法

调查采用问卷方式进行，通过文献梳理学习，自编“初中学生数学原理学习状况的调查问卷”，在2020年7月上旬学年即将结束之际，向工作室学员所在学校的学生发放问卷，要求在30分钟内闭卷回答，回收到初中三个年级学生的有效答卷400份. 其中，七年级、八年级各100份，九年级200份.

3. 数学原理学习状况的评价维度

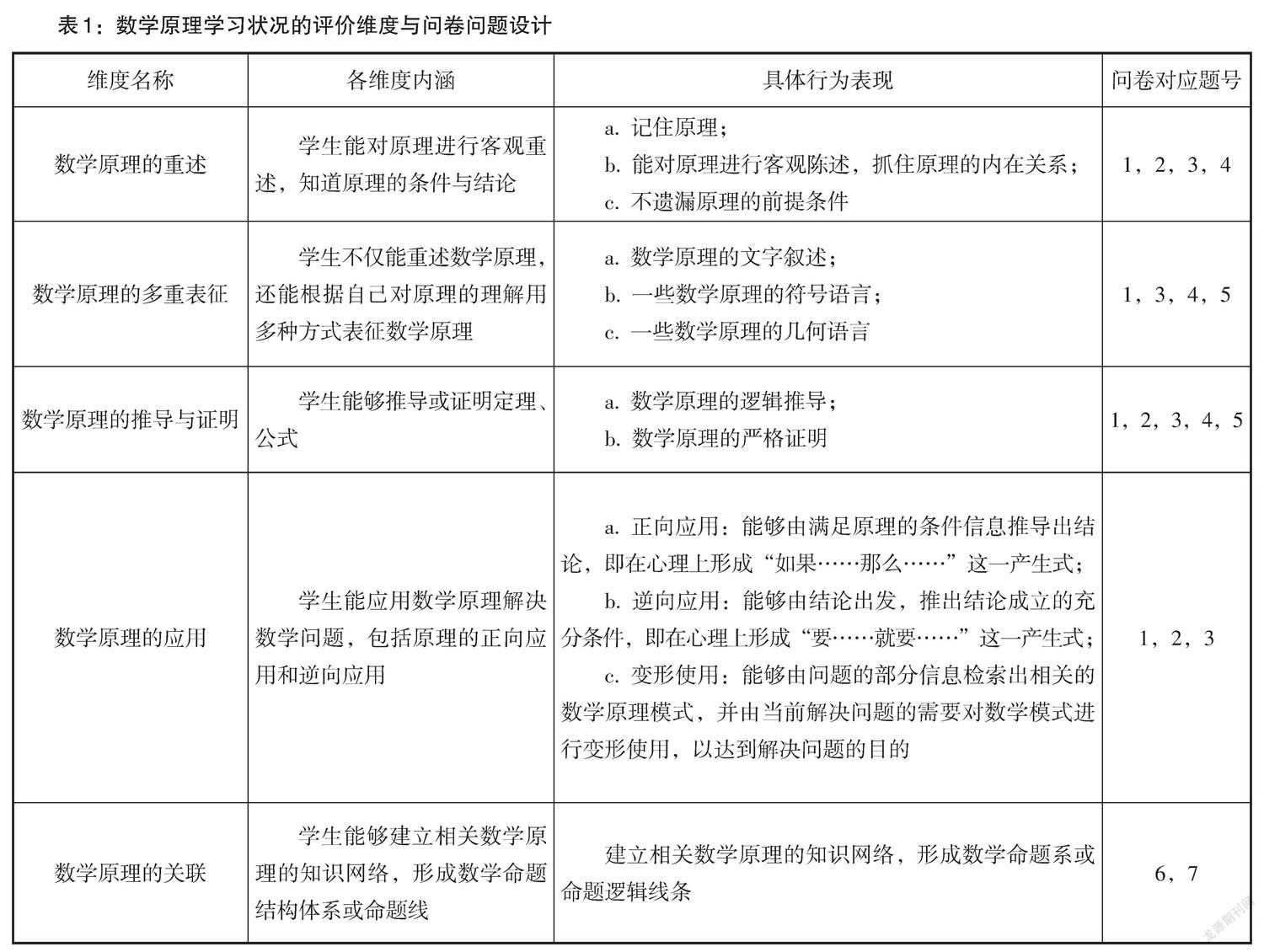
根据有关文献，我们将数学原理学习状况的评价维度确定在数学原理的重述、数学原理的多重表征、数学原理的推导与证明、数学原理的应用和数学原理的关联五个方面，并与调查问卷的各问题对应起来，具体如表1所示.

三、结果与分析

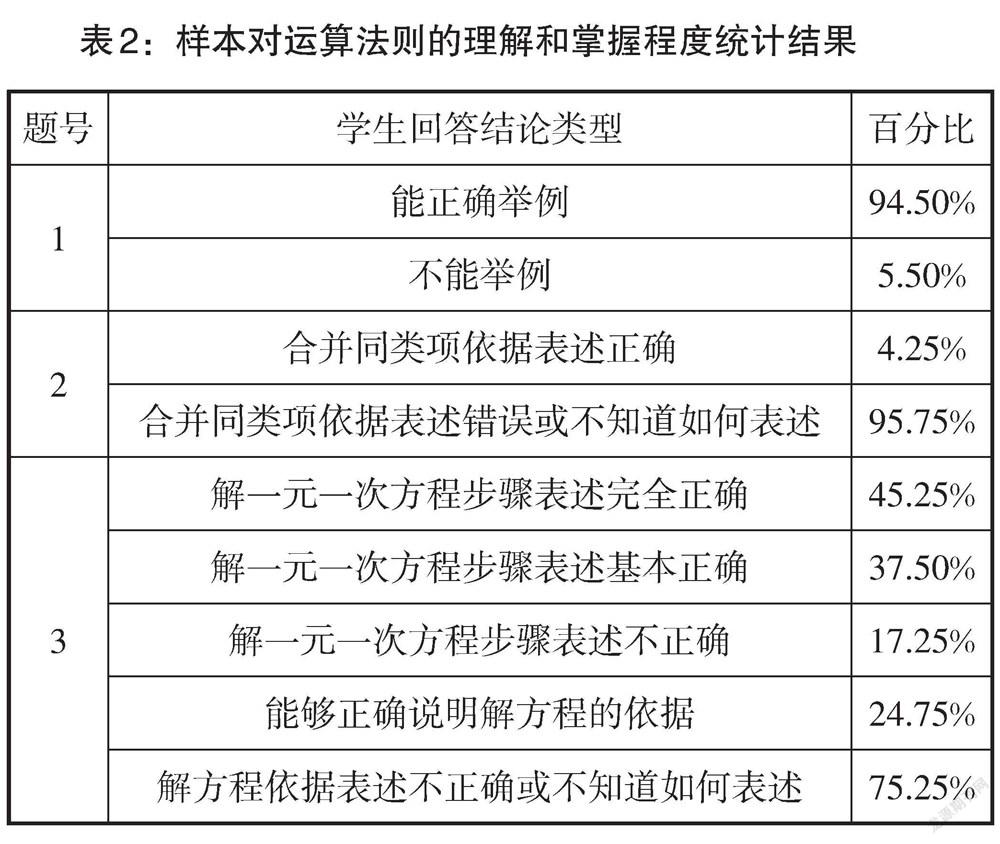
1. 运算法则的理解程度不高

调查结果显示，初中学生对运算法则的理解和掌握程度并不乐观. 对问卷所给的简单的数式运算、解方程等，大多数学生都能正确算出结果，但不懂算理的现象却相当普遍. 由表2可以看出，有95.75%的学生对合并同类项的依据表述错误或不知道如何表述;有17.25%的学生对解一元一次方程的步骤表述不正确;更有75.25%的学生对解方程的依据表述不正确或不知道如何表述.

在回答第2题“计算：[-2x+5x-6x=]     ，运算的依据是     ”时，所有的学生都能运算正确，但对运算依据的理解极不到位. 多数学生填写“合并同类项”，把内容名称与运算依据混为一谈. 有的学生就是表述具体的操作过程，如“-2x + 5x = 3x，3x - 6x = -3x”“先把两个负数加起来，再与正数相加”“x都是相同的数，拿出来后，即（-2 + 5 - 6）x，最后得出结果”“未知数不管，数字之间加减”. 也有一部分学生表述张冠李戴，如“化简求值”“提取公因式”. 还有的学生可能从来都没有想过这样的问题，如回答“不知道怎么说”.

在说明第3题“解方程[x+13=x2]时，要有哪些步骤？解方程的依据是什么？”时，解方程步骤表述完全正确的只有45.25%，七年级学生可能因为学习时间更近，比例稍大，占56%，约有37.5%的学生只是部分知道，但并不完全正确，如“去分母、解方程”“同时乘6，再合并同类项”“移项、变号、系数化为1”“交叉相乘，化简、计算”，答案中均有瑕疵. 有的学生表述为此方程的具体过程，如“2（x + 1） = 3x，2x + 2 = 3x，x = 2”. 而对于解方程的依据，仅有24.75%的学生表述正确为“等式性质”，更多学生是留空或以自己的语言进行表述，如“等号两边值相等”. 这表明他们数学原理的表征、应用水平都很不足，许多知识是呈碎片化的状态，从而使得他们的运算能力与理想中的初中数学深度学习的要求相差甚远.

值得思考的是第1题“计算：-5 + （+2） =      ，并举一生活实例，以说明其合理性”. 试题本是一道情境开放型问题，但学生呈现的精彩实例并不多，绝大多数学生所举实例都跟费用、金额有关，如“我欠了别人5元钱，还了2元，现在还欠别人3元”“买菜，给别人5元，别人找回2元，你花了3元”等. 一方面，反映了商品经济社会对学生的潜在影响;另一方面，反映了学生的数学视野比较单一，思维不够开阔，“用数学眼光观察世界”的思维习惯没有养成，数学原理的应用水平较低.

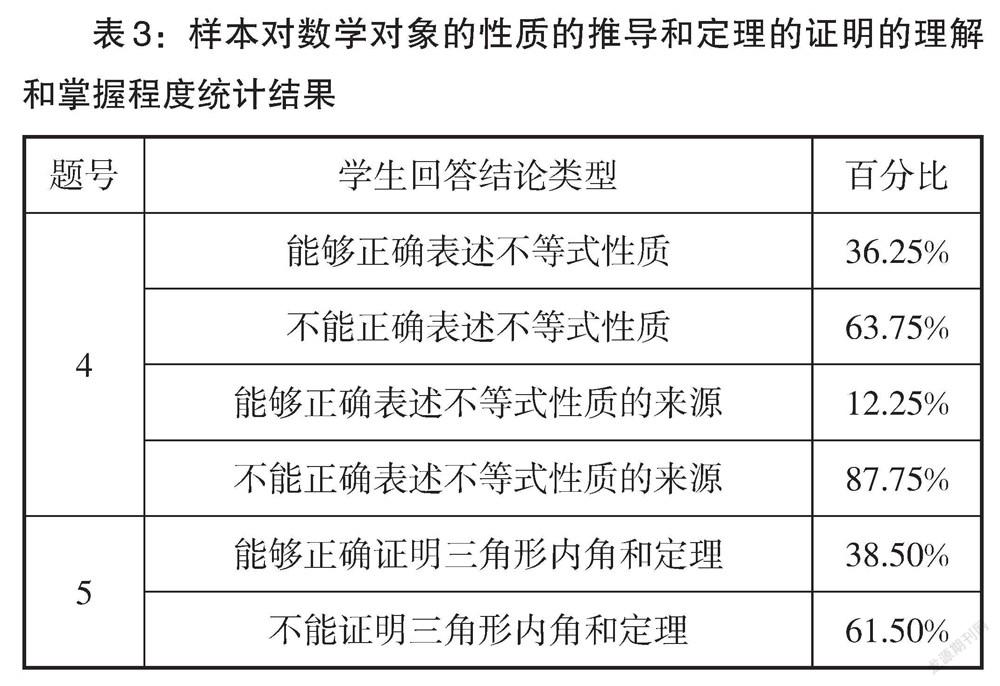
2. 对数学对象的性质、定理的推导与证明水平不高

不等式的性质是七年级下学期的学习内容. 教材上是通过类比等式的性质，以计算和比较的方式，从具体到抽象、从特殊到一般归纳推理，得到三条性质. 三角形内角和定理和勾股定理作为几何图形性质的两大基石，其重要性不言而喻. 三角形内角和更是学生在小学就已经学习过的知识，在初中的定理推导证明中，也会使用多种证法进行证明. 但表3的调查数据显示，有63.75%的学生并不能正确表述出不等式的任何一条性质，如有的学生回答成不等式的概念，有的学生的回答文字表述不清、不全，而采用符号语言表述的就更少. 有87.75%的学生不能够清楚地表述其来源，多数学生留空或乱写一通，如“听老师讲课”“书上，老师都有教”“老师说的，不晓得”. 对于三角形内角和定理的证明同样也不容乐观，有61.5%的学生不能正确证明或推理错误.

典型的错误推理有以下三类.

错证1：如图1，作AD⊥BC于点D，

因为∠ADC = ∠2 + ∠B，∠ADB = ∠1 + ∠C，

所以∠ADC + ∠ADB = ∠B + ∠1 + ∠2 + ∠C = 180°.

所以∠B + ∠BAC + ∠C = 180°.

错证2：如图2，延长BC，

因为∠1 = ∠A + ∠B，∠1 + ∠ACB = 180°，

所以∠1 + ∠ACB = ∠A + ∠B + ∠ACB = 180°.

所以∠B + ∠A + ∠ACB = 180°.

错证3：如图3，延长BC，CA，AB，

因为∠1 = ∠BAC + ∠ABC，∠2 = ∠ABC + ∠BCA，∠3 = ∠BCA + ∠BAC，

又因为∠BCA + ∠1 = 180°，∠ABC + ∠3 = 180°，∠BAC + ∠2 = 180°，

所以∠BCA + ∠1 + ∠ABC + ∠3 + ∠BAC + ∠2 = 540°.

所以∠BCA + ∠BAC + ∠ABC + ∠ABC + ∠BCA + ∠BAC + ∠BAC + ∠ABC + ∠BCA = 540°.

所以∠ABC + ∠BAC + ∠BCA = 180°.

以上三个错证，都运用了三角形的外角性质来证明，其实三角形外角性质本身是三角形内角和定理的推论，所以在逻辑上犯了循环论证的错误. 还有一种类似的错误，有些学生运用多边形的内角和公式[n-2 · 180°]，当n = 3时，得到结论，这当然也是不正确的，因为多边形的内角和公式，本身也是三角形内角和定理的推广，是通过从特殊到一般归纳得到的.而三角形内角和定理，本质上是运用平行线的性质（或平行公理），将三个内角转化成一个平角来推理证明的.

3. 对初中数学知识的整体结构和内在联系的理解和掌握不够理想

初中數学深度学习要求能够整体呈现初中数学内容的结构，以融会贯通的方式对学习内容进行组织、整合，尽可能地体现内容本质之间的联系. 由表4中的调查数据显示，仅有18%的学生能够清晰、正确地表述学习整式、函数、几何图形的基本路径，有42.5%的学生对整式、函数、几何图形的学习路径完全不知道或留空. 对于初中阶段所学的数学知识整体，只有19.5%的学生能够自觉地以一种有序的结构框架图的形式呈现.

第6题：我们学习整式（或函数或几何图形）的学习路径是怎样的？有63.75%的学生选择几何图形来回答. 这表明，几何图形的学习更容易引发学生的学习兴趣，使得学生有话可说. 同时，很多学生可能从没有思考或者听说过“学习路径”这样一种说法，表示“听不懂，不明白”. 有的学生理解为如何做一道数学题，如“先看题目条件，看图形有什么性质、定理，标记图象，作答”“先大概估测一下几何图形的特殊性，再根据相关图形的性质进行证明，完成题目（解答），不然就放弃”. 还有的学生理解成如何学习整式或几何的，如“先预习，再听课，不断写题，不懂就问”“记笔记上课专心，认真听讲，整理错题，时时刻刻想着学习，不懂就问”. 从SOLO分类理论来看，这些回答的结构大都属于前结构、单点结构，远没有达到高阶思维的水平层次. 根据调查问卷的结果，特别引起我们不安的是：无论选择哪个内容，都有相当多学生的回答映衬出了当下的应试教育生态，“数学学习就是大量做题”的错误观念几乎成为他们看待数学学科的全部：“先自己自学一遍，然后再听教师讲一次，查漏补缺，课后多练题”“多做导教导学案，课堂导学案，课堂大考卷，课时分层作业本”“多刷题，摸清规律，一般给出什么题型，学会运用定理”“先学会知识点，再运用并多次练习”“通过不断地做题、刷题，看每一个星期的数学周测和老师让学生在课堂上做的练习题，课本的教学、归纳总结，周末作业”“听课，看练习册，做题，学习函数原理”. 这些表明了学生平时长期处在一种简单、粗暴的浅层学习状态.

第7题：试用合适的方式梳理表述到目前为止你在初中阶段学过的所有数学知识. 有68%的学生是在简单地罗列所学的数学知识，想到哪写到哪，没有逻辑顺序，支干不分. 有的学生既罗列章节名称，也罗列某个具体的定理或结论;有的学生列举出的知识条目达58条之多，还有的学生是没有任何组织地直接把数学课本目录抄写了一遍. 这说明他们欠缺思维表达的方式，数学知识的整体性结构意识薄弱，数学概念、数学原理之间的关联度不高，知识碎片化严重.

四、教学建议

初中数学深度学习是对数学知识本质的理解，对知识内在联系的认识和整体把握. 数学原理的学习，要改变忽视思维教学、依靠大量机械刷题以增加考试分数的现象. 数学教育家傅种孙先生曾经说过，几何之务不在知其然，而在知其所以然;不在知其然，而在知何由以知其所以然. 这里所说的虽然是几何学习，但同样应当成为数学原理学习的指路明灯.

1. 以SOLO分类评价构建数学原理学习的目标层级

深度学习要求学生能够掌握学科的核心知识，把握学科的本质和思想方法. 数学原理的学习，当然不只是满足于知道数学原理是什么.《义务教育数学课程标准（2011年版）》（以下简称《标准》），对初中数学原理学习内容和结果目标的描述通常为：了解（同类词：认识）、理解（同类词：会）、掌握（同类词：能）、应用（同类词：证明）. 例如，“掌握有理数的加、减、乘、除、乘方及简单的混和运算”“掌握平行线的性质定理：两条平行直线被第三条直线所截，同位角相等”“了解平行线性质定理的证明”.“了解、理解、掌握、应用”借鉴了布鲁姆的认知技能目标分类理论，其具体内涵如图4所示.

对照这个目标，由调查数据可以看出，很多学生对数学原理的学习花费了很多时间，刷了许多题目，但其实学习的层级很低，学生对很多数学原理的学习并没有达到理解的目标层次.

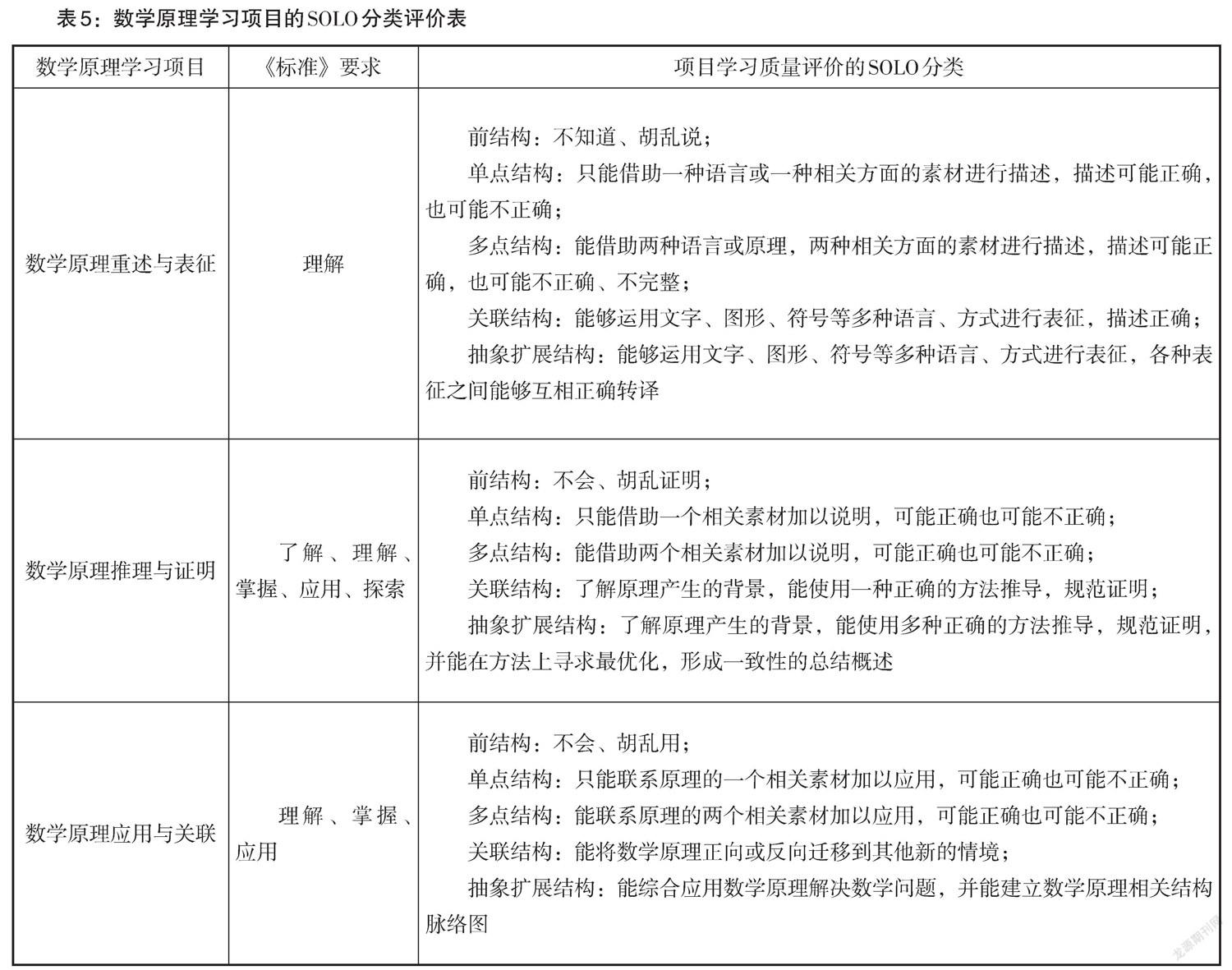
當然，认知结果四个层级目标是对所有数学内容学习结果的评价，并不特别针对数学原理的学习. 从数学原理学习目标要求出发，可以借鉴SOLO分类理论进一步精准建构数学原理学习过程的评价层次框架.

基于SOLO分类理论，我们根据数学原理学习关注的三个核心，即是什么、从何而来、迁移应用，在符合《标准》要求的基础上，设置典型的评测问题，根据学生回答的表现，由低到高划分成前结构、单点结构、多点结构、关联结构和抽象扩展结构五个不同的思维结构层次，以此来精准调控数学原理学习的达标情况，具体如表5所示.

2. 加强数学原理学习的过程教学

初中数学深度学习要求学生在经历知识产生的过程中体会其中的思想方法，形成数学的思维方式.《标准》中，对很多原理的教学要求，还有“探索”“探索并证明”. 什么是探索呢？探索是独立或与他人合作参与特定的数学活动. 在活动中，发现问题和提出问题，分析问题的思路，发现数学对象的组成要素或相关要素之间的关系，以及与其他相关对象之间的关系，从而获得一定的理性认识. 史宁中教授说过，智慧表现在过程之中. 学生会想问题，会做事情，在本质上是学生自己在过程中悟出来的. 我们要创造一个过程，让学生亲身经历的过程，让他们在想的过程中学会想，让他们在做的过程中学会做. 所以，数学原理的学习，一定要加强原理获得的过程和原理证明的过程，也就是知识的发生、发展过程. 没有过程的体验，也就没有感悟，也就没有经验的积累，无法形成理性的认识. 只会做题而依据全都不知道的运算能力可信吗？理解运算法则、懂得算理是有效提高运算能力的必要条件，帮助学生体会运算法则的意义和合理性，才是运算法则教学的根本. 抛开过程的体验，换以大量的重复训练，这是本末倒置、急功近利的短视行为. 性质定理的学习也是如此，不能推导或证明，不能做到知其所以然，也就没有达到有效、深刻的理解层次，思维能力的培养也就无从谈起.

同时，习惯性地跳过原理过程的学习，将数学原理的学习变成大量刷题训练，对学生的情感、态度、价值观的形成有促进作用吗？真的有利于他们的终身发展吗？我们可以根据如表6所示的国家义务教育质量监测数学学习情感、态度相关指标来加以判断.

从全国范围来讲，有近四成的学生对数学学习普遍感到焦虑，缺乏自信心. 所以，从初中数学深度学习出发，在原理学习过程中，通过精心设计问题情境，引发学生认知冲突和深度思考，经历原理学习的发生和发展过程，既是学科本质的要求，又是现实的呼唤.

3. 加强数学原理关联知识结构的整体教学

数学是一个整体，构建一个逻辑连贯、前后一致、迁移能力强的数学认知结构始终是数学教学的核心任务. 数学原理与数学概念一样，都是这个认知结构大厦中的核心材料. 一个数学原理并不是孤立存在的，它一定连接着数学概念、数学原理，所以数学原理的学习也要加强数学整体性的认识，注重揭示数学原理与原理、数学原理与概念、概念与概念之间的联系，构建原理学习的整体网络结构体系. 以三角形内角和定理为例，在小学阶段，学生是有操作了解并简单应用三角形内角和定理结论的，但在初中阶段，我们不仅要重点探索并证明三角形内角和定理本身，还要在学习过程中，以联系的、整体的观点，呈现出三角形内角和定理的来龙去脉，相关联的一系列概念、原理的知识结构网络（如图5），是一个有逻辑的、具有发展性的、不断拓展放大的结构网络.

在数学原理学习过程中，综合以上教学建议，在不违背《标准》要求的背景下，采用SOLO分类目标层级框架评价原理学习的结果质量，仿照波利亚“怎样解题表”的形式，构建了数学原理学习实施路径（如表7）.

总之，我们一致认为，要在数学原理的学习过程中注重引导学生对数学原理内容积极主动地理解，建立有关联的整体结构，设计有效的数学活动，让学生去经历、探索数学原理产生、说理或证明的过程，感悟其中的数学思想方法，形成数学的思维方式，达到“知其然、知其所以然、何由以知其所以然”的境界，并将获得的数学原理等知识、方法应用于现实世界，解决现实问题，以实现初中数学原理的深度学习.

参考文献：

[1]刘晓玫. 深度学习：走向核心素养（学科教学指南·初中数学）[M]. 北京：教育科学出版社，2019.

[2]吴有昌，高凌飚. SOLO分类法在教学评价中的应用[J]. 华南师范大学学报（社会科学版），2008（3）：95-99，160.

[3]JOHN B BIGGS，KEVIN F COLLIS. 学习质量评价：SOLO分类理论（可观察的学习成果结构）[M]. 高凌飚，张洪岩，译. 北京：人民教育出版社，2010.