基于CCRAA熵值模型的双向顶推钢混组合梁风险评估

李丽超，薛洪运，崔凤坤，葛颜慧

(1.山东科技大学 土木工程与建筑学院，山东 青岛 266590;2.山东交通学院 交通土建工程学院，山东 济南 250300)

0 引言

随着蒙华铁路跨汉宜高铁特大桥、泸州长江大桥等桥梁的成功建设与应用，桥梁技术在顶推施工领域取得了突飞猛进的发展。桥梁顶推施工是将梁体在桥跨两侧沿桥纵轴线方向逐段拼装完成，在千斤顶顶推作用下沿纵向滑移至预定位置，最终降落就位的一种桥梁施工方法。该施工方法既避免了桥梁施工对既有线路的运营干扰，也降低了安全风险发生的概率。然而，与传统的支架现浇、预制吊装等桥梁施工工艺相比，桥梁顶推施工跨度大，施工技术难度高，不确定因素复杂，存在很大的安全风险隐患。因此，为提高桥梁在顶推施工过程中的整体安全性，有必要进行全面的风险源辨识和整体风险评估。

目前，国内桥梁施工风险分析取得了一定研究成果，常用的桥梁施工风险评估方法包括层次分析法、LEC法、结构失效概率法、肯特指数法、有限元法、蒙特卡罗算法、模糊综合评判法等[1-4]。杨磊[5]应用有限元分析、模糊综合评判理论对顶推施工进行等级划分，并提出了相应风险控制措施，虽然客观性强，但是解释性弱。张运涛[6]运用层次分析法、模糊数学理论、定性与定量相结合的方法对钢混组合梁施工进行风险分析，但层次分析法过度依赖专家主观臆断，结果误差大。贾布裕[7]采用FORM算法和有限元可靠度分析理论对钢混组合梁上部结构施工进行风险分析，虽然解释性强，易于人接受，但计算结果分散性强，实用性低。

由于上述桥梁施工风险分析方法存在局限与不足，因此提出基于修正的LEC法和CCRAA熵值模型综合评判的施工风险评估方法。采用补偿竞争风险聚合算法(Compensation Competition Risk Aggregation Algorithm，CCRAA)对各指标权重值进行权重补偿，实现权重值的聚合收敛，降低主观臆断与客观片面带来的影响。通过某大悬臂双向顶推钢混组合梁桥的实例分析，构建实用的大悬臂双向顶推钢混组合梁桥施工风险分析模型，保证桥梁施工安全。

1 确定风险因素指标值

安全生产LEC(Likelihood Exposure Consequence)评价法起源于美国，是对具有潜在危险性作业环境中的风险源及风险因素进行半定量的安全评价方法[8]。根据修正的LEC评价法和《公路桥梁和隧道工程施工安全风险评估指南》[9]确定风险因素指标值，具体计算公式为：

U=LEC，

(1)

式中，U为风险指标值；L为发生事故的可能性大小；E为暴露于危险环境的频繁程度；C为发生事故产生的后果。

在大悬臂双向顶推钢混组合梁桥施工过程中，应避免施工安全管理制度、管理水平及现场实际操作规程的不同，而造成项目整体风险评估等级误差较大的后果[10-11]。张雪等[12]通过安全生产管理补偿系数对转体施工桥梁的各风险指标值进行风险补偿，最终得到风险源等级，但未给出安全生产管理补偿系数的具体取值，具有一定模糊性。此处针对大悬臂双向顶推钢混组合梁桥施工特点，结合专家及现场管理人员经验，通过引入风险调整系数k，分别对特大、重大、较大、一般、较小5个等级进行各风险因素指标打分与计算,计算公式为：

U=kLEC，

(2)

式中k为风险调整系数，一般取经验值0～2.5。

风险指标值U越大，说明风险源存在的危险性越高，施工过程中事故发生的可能性越大，造成的人员伤亡和财产损失越大，需要加强风险控制措施。

2 基于CCRAA熵值的风险综合评估模型建立

以层次分析法、熵权理论、CCRAA、模糊数学理论为基础的CCRAA熵值的风险综合评估模型，是在大量吸收专家经验和学识的前提下，考虑大悬臂双向顶推钢混组合梁桥施工风险因素的不确定性等问题，对多指标风险因素进行风险聚合优化计算的理想方案。利用熵权法与CCRAA模糊聚类特点[13]，解决施工风险体系中各风险因素的权重问题。根据经典的模糊综合评判法计算各指标特征值的模糊矩阵，对比隶属度函数，最终完成大悬臂双向顶推钢混组合梁桥施工风险源辨识与风险等级的确定。

2.1 建立风险指标影响因素集

根据大悬臂双向顶推钢混组合梁桥施工方案的特点与现场管理制度，基于修正的LEC法确定风险因素评价指标值，结合富有经验的专家及现场管理人员、技术人员的意见，建立大悬臂双向顶推钢混组合梁桥施工风险层次分析模型，如图1所示。

图1 施工风险层次分析模型

2.2 构造CCRAA熵值的风险综合评估矩阵

2.2.1 建立风险指标评判矩阵

通过修正的LEC法评价各风险源D关于风险因素评判指标V的评价指标值U，确定风险因素隶属集合V=(v1,v2,…,vn)，对具有模糊性的指标值以有序三元组X=(D,V,U)进行描述。将第i个风险源的第j个风险因素构成的风险指标评判矩阵记作Xij，即：

(3)

式中，Xij为i个评判对象的j维评判矩阵；Di为第i个评判对象，i=1,2,…,m；vj为第j个评判对象的评判等级，j=1,2,…,n；Uij为第i个风险评估对象与第j个评判等级的隶属关系。

2.2.2 构造最优化风险指标评判矩阵

为提高风险因素指标值的合理性与可靠性，对风险因素指标值进行最优化处理，基于最优化原则的基本要求，针对大悬臂双向顶推钢混组合梁桥施工特点与施工步骤，采用适中型原则，计算式为：

(4)

式中，uij为评价对象最优化指标值；minDij,midDij,maxDij分别为评估对象指标值的最大值、中间值、最小值。

因此，最优化风险指标评判矩阵γij，即：

(5)

2.2.3 确定风险因素权重

权重是整个风险评估体系中衡量各风险源风险等级的重要体现。基于大悬臂双向顶推钢混组合梁桥施工工序与风险评价标准，为避免主观臆断给各风险因素指标带来的影响，采用客观赋权的熵权法确定各风险因素的权重值[14]，具体计算步骤如下。

(1)根据熵权法的定义，若有m个风险评估对象，n种风险指标对应隶属关系，在最优化风险指标评判矩阵γij中，第i个风险指标值的熵值Fui的表达式为：

(6)

式中，Fui为第i个风险指标值的熵值；n为风险指标对应隶属关系状态数目。

(2)依据计算的第i个风险指标值的熵值Fui，计算各风险指标权重Wui：

(7)

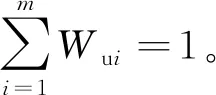
2.2.4 构造CCRAA熵值的综合评判矩阵

大悬臂双向顶推钢混组合梁桥施工属于复杂的系统工程。考虑多个风险指标之间的互相影响，为获得更加有效与实用的风险评估结果，要进行风险聚合。风险聚合常用的方法有风险值求和法、求最大风险值法、求风险质心等方法[15-16]。然而，单一的风险聚合方法都会对所得权重值产生过度依赖，导致评估结果趋于发散。因此，先对各风险指标权重值进行补偿，再聚集到类聚中心，以避免上述缺点带来的影响[17]。具体计算如下。

(1)确定风险指标聚类因子

模糊聚类是将聚类中心作为聚类单元全集的实际样本，而聚类中心是聚类全集的一个虚拟理想样本，它综合反映聚类全集的样本特性，表征其他样本的敛散度[18]。符合实际工程需要的聚类中心与样本之间的关系越收敛越好。

假设A和B是聚类单元全集C上的2个模糊子集，将实际工程应用中子集A和B之间的距离记为δ(A,B)，即：

(8)

式中，cA(xi)和cB(xi)分别为聚类单元全集中A集合与B集合在y方向的坐标值。

将理想的聚类中心样本初值设为R0，各风险指标在y方向的坐标值为Ri，则风险指标聚类因子s可表示为：

(9)

(2)风险指标特征值补偿原则

为保证风险指标聚类因子s的收敛性，就要缩小各风险特征值组成的聚类样本与聚类中心样本初值之间的距离，使聚类样本靠近聚类中心，实现风险指标值权重的风险补偿。风险补偿是通过聚类因子s对熵权法求得的各风险指标权重值进行比例分配。

设有m个风险值，将风险值由小到大排序构成风险补偿序列，聚合风险指标的权重补偿值记为Rgi，具体补偿原则为：

(10)

式中[m/2]为不超过m/2的最大整数。

(3)确定CCRAA的熵权矩阵

风险指标补偿值计算完成后，对比通过熵权法确定的各风险因素权重值，以向聚类中心样本初值R0靠近为原则，进而确定CCRAA的熵权矩阵Rfi=[Rf1，Rf2,…，Rfm]，即：

Rfi=[Rf1，Rf2,…，Rfm]。

(11)

2.3 构建模糊综合评判模型

为综合评判大悬臂双向顶推钢混组合梁桥施工风险评估结果，基于最优化原则处理得到的各风险因素指标值及构建的CCRAA熵权矩阵，采用经典的模糊综合评判法并结合隶属集合，对大悬臂双向顶推钢混组合梁桥施工风险进行等级评判，建立模糊综合评判模型Ji：

Ji=Rgi·γij，

(12)

式中Ji为各风险源模糊评估矩阵。

3 实例分析

3.1 工程背景

某大悬臂双向顶推钢混组合梁桥，双幅布置，总桥宽38 m，桥梁斜交角30°，位于直线段处，设双向2%横坡。桥面板采用架设的8 cm预制板，现浇17 cm厚混凝土桥面板。主梁为钢混组合连续梁桥，施工工艺为双向顶推施工，跨径布置为(57+59+57) m，基础为钻孔灌注桩。

主梁采用标准钢箱梁逐段焊接而成，由于施工环境不确定因素多，跨越干渠施工风险大，为避免多指标风险因素带来的人员伤亡和财产损失，在大悬臂双向顶推钢混组合梁桥施工前，要进行风险源辨识。基于修正的LEC法确定评价对象指标值，依据大悬臂双向顶推钢混组合梁桥施工工序建立施工风险层次分析模型，分别对钢箱梁焊接与拼装、钢箱梁顶推施工、横隔板安装、预制桥面板铺装、落梁施工5种风险源及对应风险因素进行风险评估，风险层次分析模型如图1所示。

3.2 建立并优化风险评估判断矩阵

根据大悬臂双向顶推钢混组合梁桥施工现场条件，分析各风险因素的特点，权衡富有经验的专家及现场安全管理技术人员的意见，运用上述修正的LEC法建立风险指标判断矩阵。然后，采用适中型的优化处理原则，获取优化后的风险评估判断矩阵。以钢箱梁顶推施工为例进行详细的风险分析与计算。

3.2.1 风险指标判断矩阵

风险指标值的大小依据修正的LEC评价法和《公路桥梁和隧道工程施工安全风险评估指南》评分原则确定。以钢箱梁顶推施工的淹溺事故为例，按照式(2)对各二级风险因素进行计算：

D=kLEC=2.1×3×1×7=44。

(13)

钢箱梁顶推施工的其他风险因素特征指标值计算同上，见表1。

表1 钢箱梁顶推施工各风险因素特征指标值

通过修正的LEC法评价各风险源Di关于风险因素评判指标Vi的评价指标值Uij，则第2个风险源的8个风险因素构成的风险指标评判矩阵Xij为：

(14)

3.2.2 风险指标判断矩阵最优化处理

在风险源辨识过程中，风险指标特征值越大，表明风险发生的可能性越高，在风险评估过程中越要重视。在顶推施工前全面制订风险控制措施，降低风险带来的危害。根据式(4)～(5)对风险指标评判矩阵Xij进行适中型优化处理，得到优化后的风险指标判断矩阵γij，即：

(15)

3.3 确定风险指标权重

权衡大悬臂双向顶推钢混组合梁施工的风险因素特点，分析风险因素对施工的影响程度，进而对各风险指标值进行定量分析。根据3.2.3节的介绍，应用熵权理论对各风险指标值的权重进行求解，通过式(6)～(7)得出钢箱梁顶推施工各风险因素指标的具体计算结果，见表2。

表2 钢箱梁顶推施工各风险因素权重计算结果

3.4 构造CCRAA熵值的综合评判矩阵

依据各风险因素的权重结果及专家经验，确定大悬臂双向顶推钢混组合梁施工的权重初始值为0.1。根据式(8)～(9)，计算得到钢箱梁顶推施工风险指标聚类因子s为0.088。再基于式(10)的风险补偿原则，得到各风险指标权重的风险补偿值，见表3。

表3 钢箱梁顶推施工各风险因素权重补偿值

按比例对各风险因素权重值进行分配，以向聚类中心样本初值靠近为原则，按照式(11)，得到CCRAA的熵权矩阵Rfi，即：

Rf2=[0.094，0.261，0.118，0.103，0.09，

0.195，0.079，0.106]。

(16)

3.5 建立模糊综合评判模型

基于上述计算的大悬臂双向顶推钢混组合梁桥各风险指标的补偿权重值，根据风险评价系统分析中的隶属函数V=(特大、重大、较大、一般、较小)的对应关系，确定钢箱梁顶推施工风险源的施工等级。按照式(12)，计算可得钢箱梁顶推施工风险源模糊综合评判矩阵，即：

J2=Rf2·γij=[0.580,0.581,0.400,0.481,

0.366]。

(17)

根据上述计算方法，其他4种风险源的模糊综合评判矩阵为：

[J1,J3,J4,J5]=

(18)

大悬臂双向顶推钢混组合梁桥整体风险评估与上述计算方法一致，综合考虑各风险源的CCRAA熵权值与各风险指标的模糊评价矩阵，得到大悬臂双向顶推钢混组合梁桥整体风险评估结果J，如下：

[0.169,0.051,0.105,0.111,0.126]·

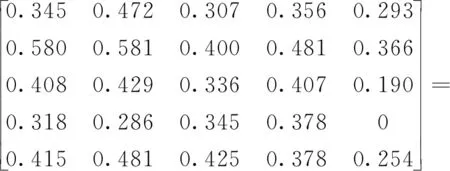
[0.218,0.248,0.199,0.220,0.120]

(19)

式中，Rgi为聚合风险指标的权重补偿值；Ji为各风险源模糊评估矩阵。

由以上计算结果并结合隶属函数可知，各风险源中，钢箱梁焊接与拼装、钢箱梁顶推施工、横隔板安装、落梁施工4种风险源为重大风险源，预制桥面板铺装为一般风险源。大悬臂双向顶推钢混组合梁桥整体风险等级为重大风险。

对于重大风险，要制订合理的风险控制措施，开展安全防范教育培训，提高现场安全管理人员及施工人员的安全意识，避免风险带来的人员伤亡和财产损失。对一般风险也不能忽略，根据安全管理制度做到零风险、无意外，保证桥梁施工安全进行。

3.6 风险评估流程

基于上述风险评估结果，本研究的风险评估方法具有合理性与有效性。目前，国内外针对大悬臂双向顶推钢混组合梁桥施工风险评估的研究甚少，为保证桥梁施工的安全开展，给出专门适用于大悬臂双向顶推钢混组合梁桥施工阶段的具体风险评估流程，如图2所示。

图2 大悬臂双向顶推钢混组合梁桥施工风险评估流程图

4 结论

本研究通过修正的LEC法确定评估对象指标值，研究了基于CCRAA熵值模型的风险综合评估矩阵在施工风险评估中的应用，给出实际工程进行风险分析，得出以下结论：

(1)基于修正的LEC法实现了大悬臂双向顶推钢混组合梁桥施工风险分析的多维变量评判，工程实例证明，引入修正系数的LEC法，不仅结果解释性强，还达到了风险指标特征值客观量化的目的。

(2)建立CCRAA熵值模型时，考虑了多指标风险因素不确定性的综合效应问题，对优化处理后的风险指标值进行了权重计算与补偿，实现了客观理论分析与主观认知的统一。合理确定风险聚合初始值，依据风险指标权重值收敛于聚类中心的原则，使补偿后的权重值向聚类中心聚合，避免了单一聚合方法对风险指标权重值的过度依赖性。

(3)基于修正的LEC法的CCRAA熵值模型的应用，对大悬臂双向顶推钢混组合梁桥施工进行风险评估，保证了专项风险指标评估的真实性与有效性。通过建立模糊数学模型及相关理论综合分析，确定了各风险源以及桥梁施工整体风险等级，给出了专门适用于大悬臂双向顶推钢混组合梁桥施工风险评估的具体分析流程。