考虑套管影响的钢绞线斜拉索索力测试方法
刘殿元,齐铁东,王晓雷
(1.交通运输部公路科学研究院,北京 100088;2.中路高科交通检测检验认证有限公司,北京 100088)
0 引言
斜拉索为斜拉桥重要构件之一,主要分为平行钢丝斜拉索和平行钢绞线斜拉索。由于平行钢绞线斜拉索可现场单根张拉,极大降低了运输及安装要求,同时后期维护时易于更换,使其在工程中得以广泛应用。斜拉桥施工过程中能否准确测量斜拉索的索力,对于指导桥梁施工、保证施工过程中的安全具有重要意义[1-2]。振动频率法由于理论成熟、操作简单、可重复测量等优点而成为最广泛的索力测定方法[3-8]。
工程上为了提高钢绞线的耐久性,通常在拉索外部安装HDPE外套管。采用频率法测定钢绞线斜拉索索力时,一般将传感器置于外套管上[9-10]。一般而言,钢绞线斜拉索在张拉完成、单根钢绞线索力调整均匀后在塔、梁锚固端附近安装拉索紧箍装置,使得内部钢绞线呈规则的六边形形状。但是拉索终张拉之前,由于斜拉索锚板的直径大于HDPE套管的直径,在斜拉索张拉过程中,HDPE外套管对内部钢绞线起环向约束作用。另外由于套管自重的原因,又会使得内部钢绞线自上而下逐层接触。钢绞线斜拉索与外套管及钢绞线内部之间复杂的接触状态,使得采用频率法测定钢绞线斜拉索索力时产生较大误差。本研究主要采用有限元法综合分析HDPE套管环向约束及自重引起的挤压接触双重作用,对钢绞线斜拉索内部接触情况进行计算分析,并提出考虑HDPE套管影响的钢绞线斜拉索索力计算公式。
1 工程概述
息县淮河大桥主桥为钢管混凝土独塔斜拉桥,桥梁全长175 m,跨径布置为(100+75)m,为塔、梁、墩三向固结体系。桥梁整幅布置,桥梁宽度为24.0 m。主梁为单箱五室预应力混凝土连续箱梁。主塔为钢管混凝土塔柱,双柱形式,桥面以上塔高为59.91 m。斜拉索采用平行钢绞线斜拉索,抗拉强度为1 860 MPa。全桥共计52根,斜拉索编号分别为L1~L13、R1~R13。桥型布置图如图1所示。
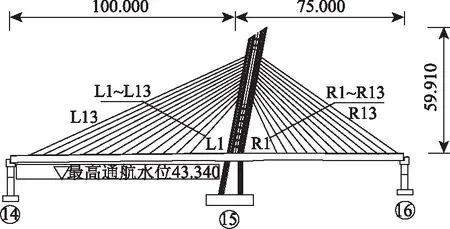
图1 桥型布置图(单位:m)
2 钢绞线斜拉索内部接触影响因素分析
根据弦张理论,工程上常用的考虑两端铰支边界条件的索力与频率的计算关系为[11]:
(1)
索力-频率计算公式为:
(2)
式中,EI为斜拉索的抗弯刚度;T为拉索的轴向拉力;m为斜拉索单位长度的质量(线密度);fn为斜拉索的第n阶振动频率;n为振动阶次;l为斜拉索长度。
采用频率法对钢绞线斜拉索索力测试时,由于外套管与所接触的钢绞线数量及钢绞线内部接触情况未知,最终导致计算时采用的斜拉索线密度与实际情况不符,所测得的频率也不能反映出拉索实际索力的大小,即通过频率法准确测得钢绞线斜拉索索力的关键在于准确分析外套管与内部钢绞线之间的接触情况。一旦确定套管与钢绞线内部接触情况后,可以将HDPE外套管的自重换算为与套管接触的内部钢绞线的线密度,即可以通过修正线密度的方式对理论计算频率予以修正。
为了分析钢绞线斜拉索内部接触情况,以R13号斜拉索为例,说明套管的环向约束作用及套管自重作用对钢绞线接触的影响。R13号斜拉索型号为15.2-61型,锚板尺寸327 mm,外套管尺寸为φ235×8 mm。斜拉索具体物理参数见表1,断面图及内部钢绞线布置图如图2所示。

表1 R13号斜拉索物理参数
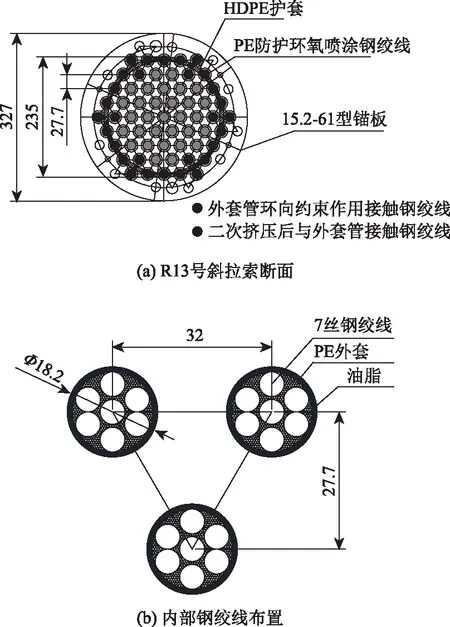
图2 R13号斜拉索断面图及内部钢绞线布置图(单位:mm)
2.1 套管环向约束作用
由图2(a)中钢绞线的孔位布置情况可知,部分孔位位于HDPE套管之外。在钢绞线单根安装、张拉的过程中至索箍安装前,图2中位于HDPE套管之外孔位的钢绞线必然因受到外套管的环向约束作用而与其发生接触。同时,由于已与套管接触的外部钢绞线因受到环向约束作用而内移,进而可能继续与内部钢绞线发生接触。套管环向约束作用主要存在于斜拉索张拉过程中,在外套管的环向约束作用下,外周钢绞线与套管发生接触连成整体。15.2-61型斜拉索中钢绞线总数量为61根,由图可知,在外套管的环向约束作用下共有32根与外套管接触,占总钢绞线数量的52.46%,即仅HDPE套管的束箍作用会导致1/2以上数量的钢绞线与套管接触。
2.2 套管自重作用
钢绞线斜拉索张拉后,由于钢绞线两端施加了张拉力,其刚度远大于HDPE外套管,计算时可忽略外套管对斜拉索刚度的影响。由于套管的环向约束作用,在重力作用下,自身重力垂直于轴线方向的分量首先由斜拉索内部外围钢绞线来承担,最外围钢绞线由于受到外套管重力作用发生下挠。
分析因外套管自重而对钢绞线产生的挤压作用时,首先按照内部钢绞线的孔位布置,将考虑套管环向约束作用而接触的钢绞线剔除后剩余钢绞线在拉索内部的相对位置进行分层,并定义各层间距离为d。
若在自重作用下,最外围钢绞线垂直于拉索轴线方向的变形量超过钢绞线层间距离,则承担外套管自重的最外围钢绞线的上层部分钢绞线会与第2层钢绞线在垂向变形量大于d的位置发生接触,外套管自重由外围钢绞线和第2层钢绞线承担,导致第2层钢绞线继续发生垂向变形。如果发生接触的钢绞线的变形量超过层间距离,则与第3层钢绞线接触,套管的重量由外围钢绞线及第2、第3层钢绞线承担。以此类推,如果套管的自重分量足够大或斜拉索索力相对较小时,会使得斜拉索内的各层钢绞线均发生层间接触[12-13]。斜拉索内部钢绞线在套管自重作用下的挤压接触变形如图3所示。
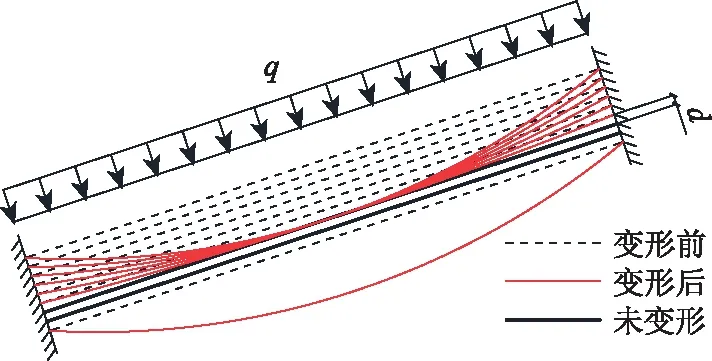
图3 拉索内部钢绞线在套管自重作用下的挤压接触变形示意图
3 考虑接触的钢绞线斜拉索自振频率计算
3.1 等效截面计算
通过以上关于钢绞线斜拉索内部钢绞线的接触过程分析可知,套管的重量除由外围钢绞线承担之外,还随着层间接触的发生而逐层传递。在计算钢绞线内部层间接触时,为了便于分析,将钢绞线截面进行等效计算,等效截面主要分为两部分,其中一部分为外围因套管环向约束而接触的钢绞线截面等效,一部分为因外套管自重作用而接触的钢绞线截面等效。等效原则为换算前后截面的面积、层间距离和抗弯刚度相同,截面等效计算如图4所示。
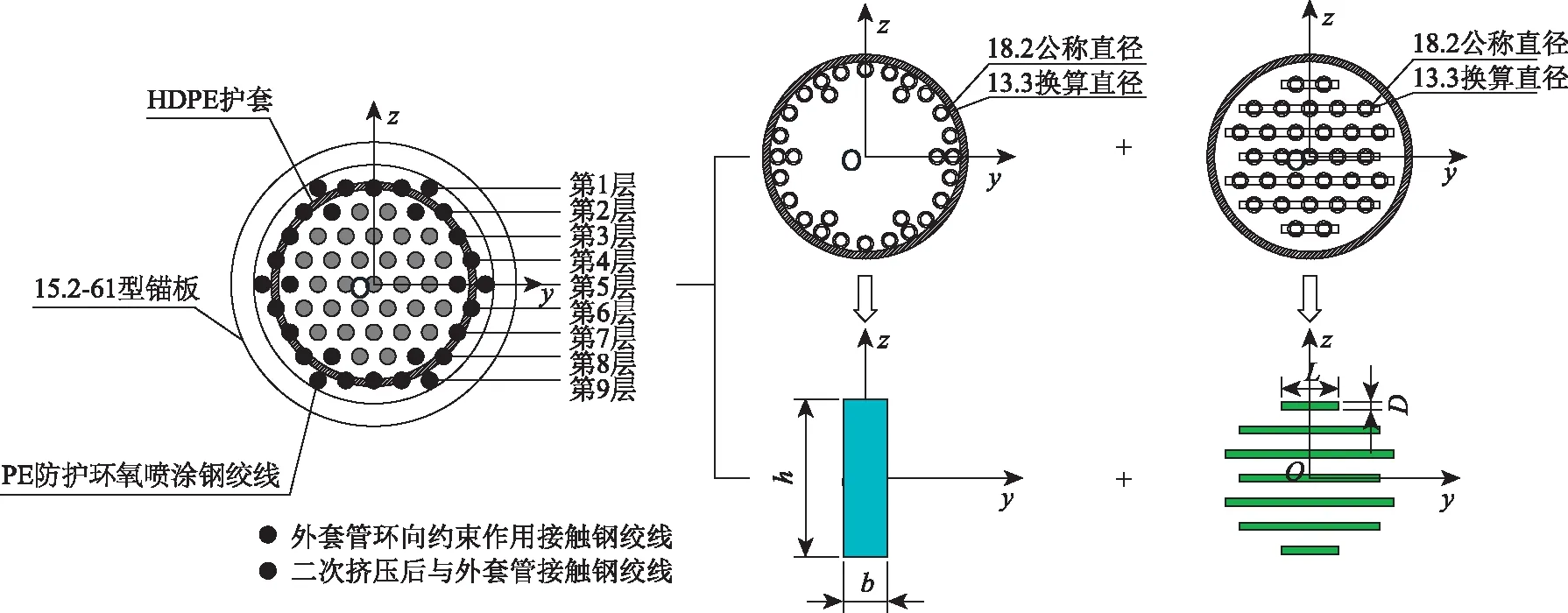
图4 钢绞线截面等效计算模型
外围钢绞线及内部分层钢绞线的等效截面计算结果如表2所示,截面换算时外围钢绞线考虑钢绞线和HDPE套管的线密度,不考虑套管刚度;内部分层钢绞线按照钢绞线的有效面积139 mm2计算,由于主要计算在套管自重作用下钢绞线逐层接触的情况,因此在截面等效时考虑抗弯惯性矩IOy及截面有效面积等效。
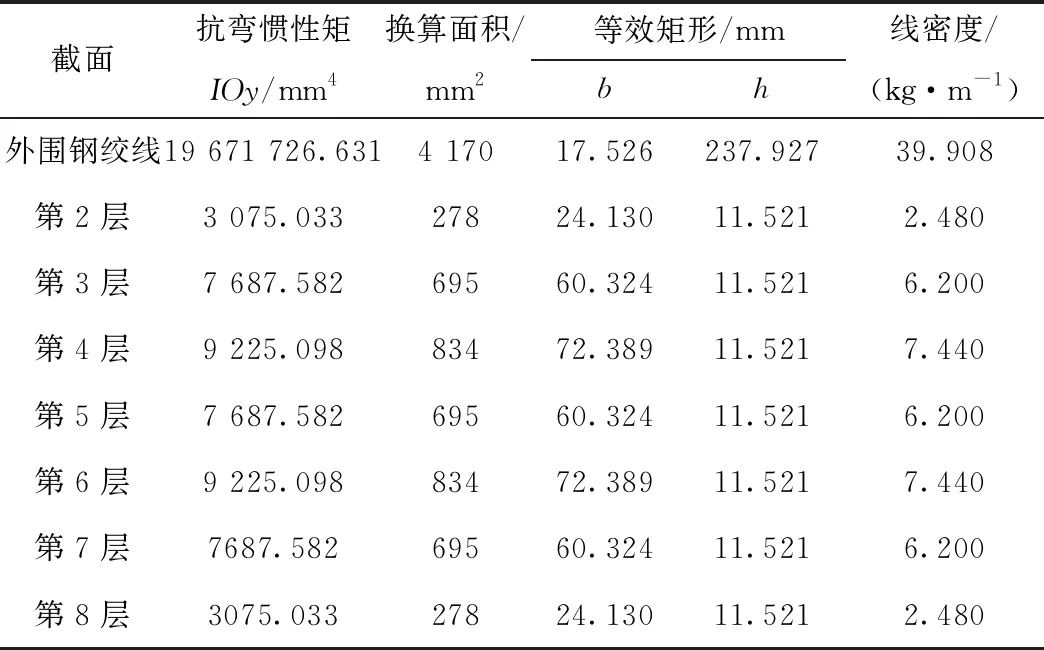
表2 等效截面计算结果
3.2 有限元模型
采用通用有限元软件ABAQUS计算内部钢绞线层间挤压接触情况,本研究接触行为的本构关系接触行为在法向采用“硬”接触,切向行为定义为库伦摩擦。ABAQUS判断两个面是否接触的条件为其面-面间距是否为0,一旦判定为接触后便在发生接触的节点上施加约束。
计算时采用8节点6面体实体单元模拟斜拉索,弹性模量取值为1.95×105MPa,线密度按照截面等效的计算结果分别赋予不同层间的钢绞线,建立的有限元模型如图5所示。
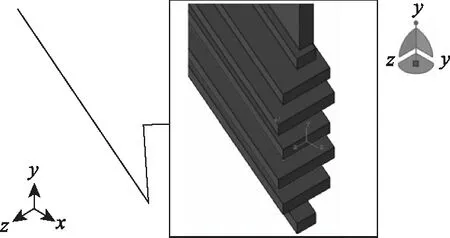
图5 有限元计算模型
通过有限元计算发现,钢绞线在套管环向约束作用及自重作用下,外围钢绞线与内层钢绞线的第2层发生接触,由于拉索索力较大,外围钢绞线与第1层接触后没有继续向下传递给第3层钢绞线。外围钢绞线等效截面底面、第2层顶面及第3层顶面的变形的计算结果如图6所示。
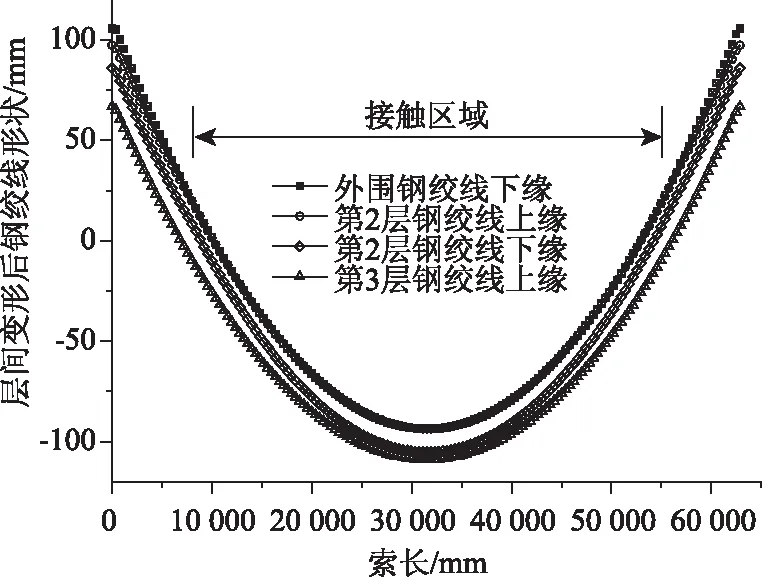
图6 钢绞线层间接触区域
由图可知,外围钢绞线与第二层钢绞线在约1/8处开始接触,至约7/8位置结束。接触后第2层钢绞线继续发生变形,但未与第3层钢绞线相接触。由此可见,R13号斜拉索首先由于套管的束箍作用,使得被约束的外围钢绞线基本可以承受套管的自重,钢绞线层间传递仅仅与第2层接触后未继续发生传递变形。
3.3 接触对斜拉索频率的影响
在外围钢绞线与第2层钢绞线发生层间接触的前提下,进行斜拉索振动分析,分别提取与套管接触钢绞线面内前6阶振型及未与套管接触钢绞线面内前2阶振型如图7所示。其中图7(a)~(f)为与外套管接触钢绞线的面内1~6阶振型,图7(g)~(h) 为未与外套管接触钢绞线的面内1~2阶振型。
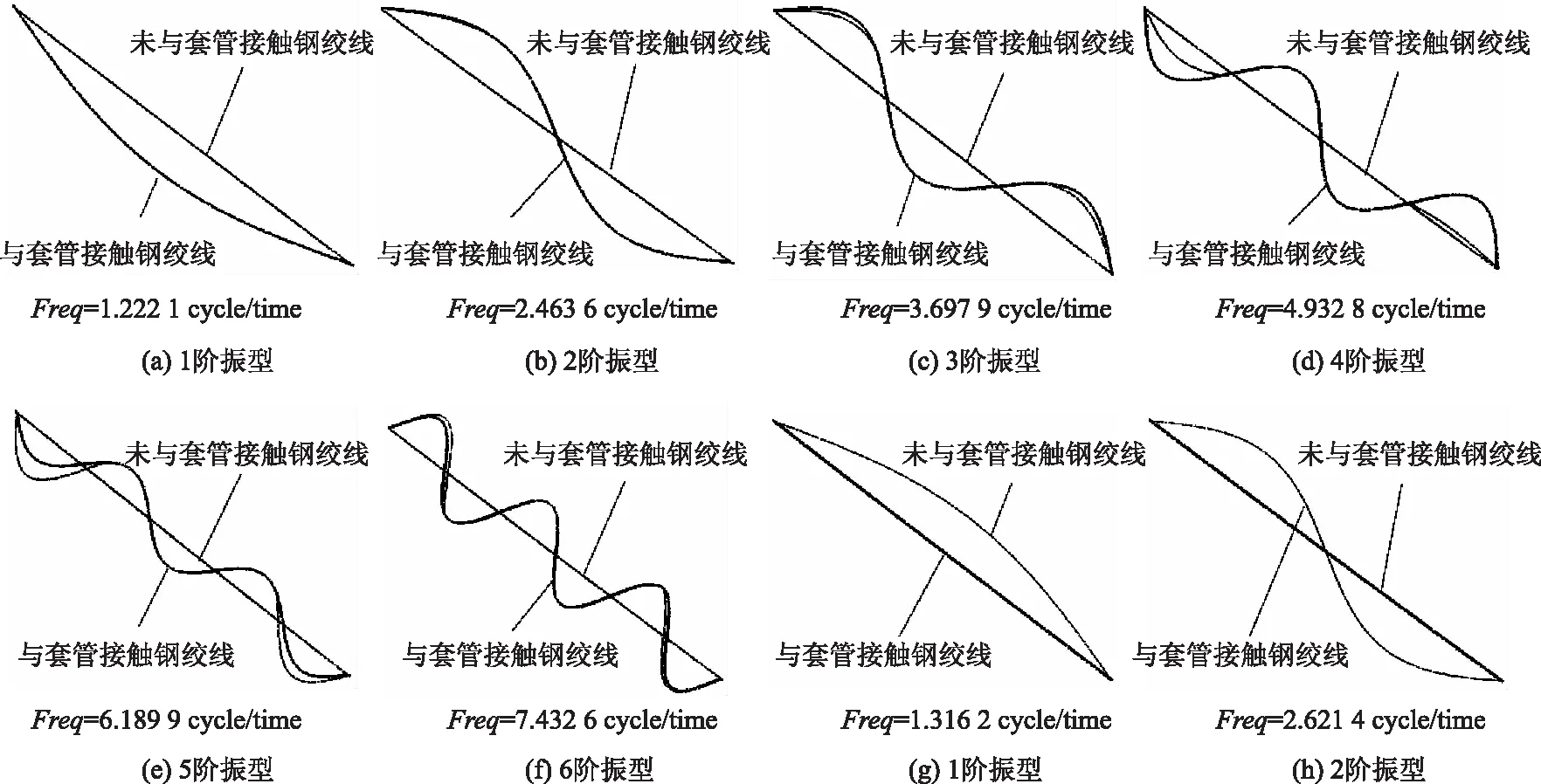
图7 R13号索钢绞线面内自振模态图
由图7可见,与外套管发生接触的钢绞线表现为与外套管一致振动,未发生接触钢绞线表现为独立振动。与外套管发生接触钢绞线的自振频率f1=1.222 1,f2=2.463 6,未发生接触的钢绞线自振频率f1=1.316 2,f2=2.621 4。由于外套管附着在外围及第2层钢绞线,与钢绞线接触后其自重由外围及第2层钢绞线承担。相同斜拉索索力前提下,与外套管发生接触的钢绞线自振频率小于未与外套管接触的钢绞线同阶次自振频率。另外由图7可知,对于3阶以上的振型,未与外套管接触的钢绞线产生明显的“层间剥离”现象,随着模态阶次升高,出现层间剥离钢绞线振动为主的干扰振型。
采用频率法测试斜拉索索力时,一般选择将传感器放置于梁端附近,对于高阶振型频率的数据采集,传感器的摆放位置可能会对其产生影响,实测时尽可能选择一阶频率,同时尽可能将传感器的摆放位置远离梁端及塔端。
4 钢绞线斜拉索索力测定公式修正
确定外套管与钢绞线内部接触情况后,可通过对拉索-频率常用计算公式予以修正,准确计算钢绞线斜拉索理论自振频率。拉索-频率修正计算公式为:
(3)
式中,EI为斜拉索内单根钢绞线抗弯刚度;T为拉索单根钢绞线的轴向拉力;mk为钢绞线换算线密度,mk=m1+m2/(k1+k2),其中m1为钢绞线线密度,m2为HDPE外套管的线密度;k1,k2分别为束箍作用导致的外围钢绞线与套管接触的根数,和套管自重导致的内部钢绞线层间接触的根数,其中k1数量通过拉索的型号及套管的尺寸确定,k2通过有限元分析确定;fn为斜拉索的第n阶振动频率;n为振动阶次;L为斜拉索长度。
息县淮河大桥R13号索在施工过程中分3次张拉,各张拉阶段采用修正后公式法的计算1阶频率与有限元法计算的1阶频率结果如表3所示。由表3可知,与未修正公式法相比,采用修正后的公式法计算的斜拉索各张拉阶段1阶频率与有限元法计算结果一致,二者最大偏差为0.63%。
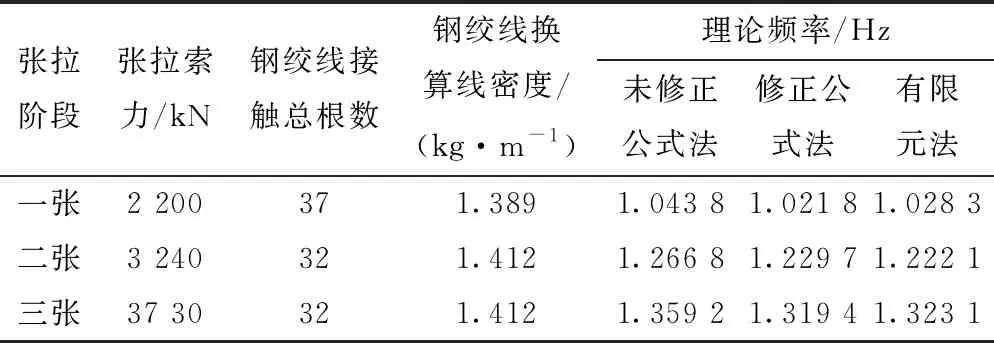
表3 R13号斜拉索1阶频率计算对比
采用频率法测试斜拉索的索力时,需考虑拉索两端的边界条件、索的刚度及线密度等对拉索计算长度、振动频率的影响。公式(3)为基于弦张理论假设拉索边界为铰接得到的,而斜拉索的支撑条件介于铰接和固结之间[14],常见的边界条件处理方法为考虑锚具的影响对计算索长进行修正。另外需要通过对比锚下张拉力,对斜拉索的实际刚度、线密度进行参数识别[15-18],斜拉索张拉过程中的锚下张拉力可通过锚下传感器或千斤顶油压传感器测得。本研究中的方法主要解决钢绞线斜拉索张拉过程中的索力测试的问题,此时拉索减震阻尼未安装,而对于成桥后的索力测试还需考虑钢套管部位的减震阻尼对拉索振动频率的影响。
经过参数识别后的斜拉索实测索力与锚下张拉力的对比结果如表4所示。
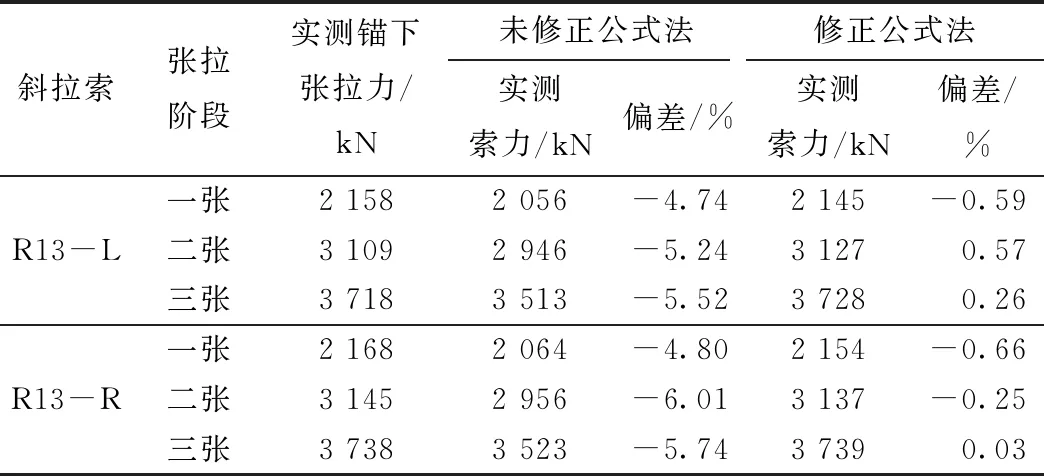
表4 R13号斜拉索实测索力对比
由表4中采用频率法的测试结果与实测锚下张拉力的对比结果可知,与修正前相比,根据修正后的公式计算实测索力与锚下张拉力的实测结果更为接近,也验证了此方法在钢绞线斜拉索索力测试时的准确性。
5 结论
本研究以息县淮河大桥为背景工程,采用有限元法分析HDPE外套管对钢绞线斜拉索振动频率的影响,并提出拉索-频率常用计算公式的修正方法。得到如下研究结论:
(1)HDPE外套管对钢绞线斜拉索振动频率的影响因素主要为套管环向约束作用及自重引起的挤压接触作用,分析外套管与内部钢绞线之间的接触时,需对两种因素进行综合考虑。斜拉索张拉过程中,HDPE外套管的自重主要由外围钢绞线承担。
(2)分析结果表明,与外套管发生接触的钢绞线自振频率小于未与外套管接触的钢绞线同阶次自振频率。随着模态阶次升高,出现以层间剥离钢绞线振动为主的干扰振型。采用频率法测试时传感器的位置尽量避开梁端、塔端位置,建议实测时尽可能选择一阶频率。
(3)通过综合考虑套管环向约束及自重的双重作用,对拉索-频率常用计算公式进行修正,修正后的计算结果与有限元计算结果一致。同时结合依托工程现场实测基频结果验证了外部护套与内部钢束的振动一致性,索力监测时可以直接在外部套管上安置拾振器测量斜拉索的振动频率。结合参数识别,考虑外套管影响修正后的索力测试结果与实际张拉力更为接近,该方法可应用于实际工程。

