基于平行控制理论的循环流化床锅炉床温智能预测模型

刘文慧，严博文*，吴江，任一君，孔维政，谌际宇

（1.内蒙古蒙泰不连沟煤业有限责任公司煤矸石热电厂，内蒙古准格尔 010321；2.华北电力大学控制与计算机工程学院，北京 102206）

0 引言

随着可再生能源的发展和社会环保意识的增强，火电机组在灵活性和污染物排放方面受到了严格的限制。由于在燃料适应性、污染物控制和负荷调节方面的优势，循环流化床（CFB）燃烧技术在过去50年取得了重大进展［1］。到2017年，中国有超过4 000台CFB 锅炉机组，总容量超过100 GW［2］。CFB燃烧技术正朝着更高参数、更大容量的方向发展。到2020 年，已经有46 台超临界CFB 锅炉投入使用，总容量接近17 GW［3］。

随着我国能源革命的发展，碳中和背景下以新能源为主体的新型电力系统加速构建，越来越多的间歇性可再生能源，如风能、太阳能以及分布式发电系统接入电网，火电机组面临着快速变负荷、超低负荷的运行要求，为火电机组的安全稳定运行带来了挑战。CFB锅炉机组运行参数的精准预测模型可以为现场运行提供指导和帮助，从而提高机组运行的安全性与稳定性。许多研究发现，维持正常床温是CFB 锅炉稳定运行的关键［4］，机组运行过程中，几乎所有的控制和调节都是围绕维持稳定的床温进行的。床温预测可以通过研究锅炉燃烧过程，求解质量和能量守恒方程，建立基于力学的模型［5-6］。然而，床温的影响因素有很多，如各因素之间的耦合、大延迟效应以及炉内气固两相流特性都会导致机理模型较为复杂，不适合现场控制系统的设计和优化［7］。在实践中，力学模型所需要的变量有时难以获得，因此，大多数基于力学的床温预测模型存在精度不足的问题。平行控制系统的理念最早于2004年由王飞跃提出［8］，基于平行系统的理念，利用智能算法构建虚拟系统，实际系统不断向虚拟系统提供数据和支撑，虚拟系统则利用寻优、预测等手段为实际系统的运行提供指导和帮助，为机理模型的不足提供了解决办法。

随着计算机技术的发展，机器学习越来越多地应用在工业领域。文献［9］分析了近年来利用神经网络算法预测脱硫系统SO2排放量的算法网络结构、输入参数等算法细节，讨论了神经网络算法应用于脱硫系统的特点。倪绍佑［10］利用反向传播（BP）神经网络对CFB 锅炉的SO2排放进行了建模，发现以锅炉蒸发量、一次风量、烟气含氧量等作为模型输入时的建模效果最佳。张媛媛等［11］利用BP神经网络算法构建了NOx排放质量浓度预测模型，并采用遗传算法优化了BP神经网络的权值和阈值，通过建模确定了机组在100 MW 超低负荷下的主要优化参数。韩义等［12］利用BP 神经网络对某300 MW 循环流化床机组进行建模以预测机组出力，通过数据预处理减少异常数据对模型精确度的影响，通过主成分分析法（PCA）降维减少输入变量个数,预测结果具有较好的精确性与稳定性。崔博洋等［13］将提取的电厂厂级信息监测系统（SIS）数据库数据特征作为长短期记忆（LSTM）神经网络的输入，得到脱硫吸收塔pH 值预测模型。受这些研究的启发，本文采用基于时序注意力机制的长短期记忆（TPA-LSTM）神经网络模型对床温进行建模，以“时序片段关注模式”替代传统注意力机制的“点关注模式”。机组试验数据表明，TPA-LSTM 模型取得了更好的预测效果。本文的预测模型能够根据现有测点数据预测出未来20 s 的床温值，可为进一步的机组运行提供参考。

1 理论背景

1.1 CFB锅炉运行简介

CFB 锅炉运行过程中，煤矸石经干燥粉碎后与石灰石混合进入锅炉，在一次风的作用下以“流化”状态进行燃烧发热。为保证煤粉完全燃烧，通常在炉壁的不同高度安装二次风喷嘴，为燃烧提供充足的氧气。一次风由炉膛底部的布风板吹出，以保证床料的流动性，二次风出口通常布置于炉壁周围，为燃烧提供足够的氧气。燃烧产生的烟气经由水平烟道进入旋风分离器。在旋风分离器中，较重的颗粒被分离并返回炉膛进行再循环，未燃尽的煤和石灰石被循环回收，提高了燃料的燃烧效率以及石灰石的利用率。

双支腿型CFB 锅炉部分结构如图1所示。床层中的混合颗粒由部分燃烧的煤、石灰石及灰分组成，床层物料会因直径和密度的不同而发生分离，大颗粒大多停留在炉底，定期排出炉外，只有细颗粒才能被通过炉膛的烟气携带。

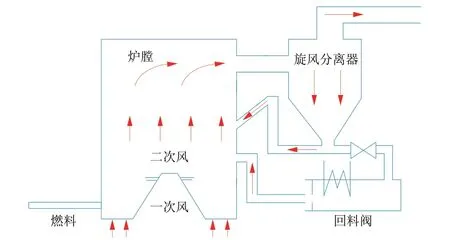
图1 双支腿型CFB锅炉部分结构Fig.1 Partial structure of a pant-leg circulating fluidized bed boiler

床温通常指物料在密相区的温度，它对CFB 锅炉的安全运行起着重要的作用。床温是燃烧过程中关键的受控变量，具体来说，床温越高，焦炭的挥发和反应速度越快，锅炉的燃烧效率也就越高。床温受锅炉负荷、给煤量、煤质、一次风量、二次风量、灰渣排放等因素的影响；同时，床温表征了炉内燃烧情况，较高的床温往往会有较快的变负荷速率，但会导致更多的污染物生成。在超低负荷运行、快速变负荷以及超低排放三大要求下，床温成为平衡这些要求的重要参数。在动态运行过程中，床温不可能保持在一定的温度范围内，因此，若能对床温进行提前预测，则可为现场运行策略调整带来新的思路。本文研究了床温的单点预测，提供了床温未来的变化信息，对床温的控制和预警具有重要意义。

1.2 平行控制系统理论

平行控制系统旨在指导实际系统与虚拟系统的交互，促进两者的协同发展。平行系统指由实际系统和对应的虚拟系统所组成的共同系统，如图2所示。通过构造与实际系统对应的虚拟系统，采取在线学习、离线计算、虚实互动等技术，使得虚拟系统成为运行实验室，以计算试验的方式为实际系统的运行提供借鉴、预估和引导，从而为企业管理运行提供高效、可靠、适用的科学决策和指导。

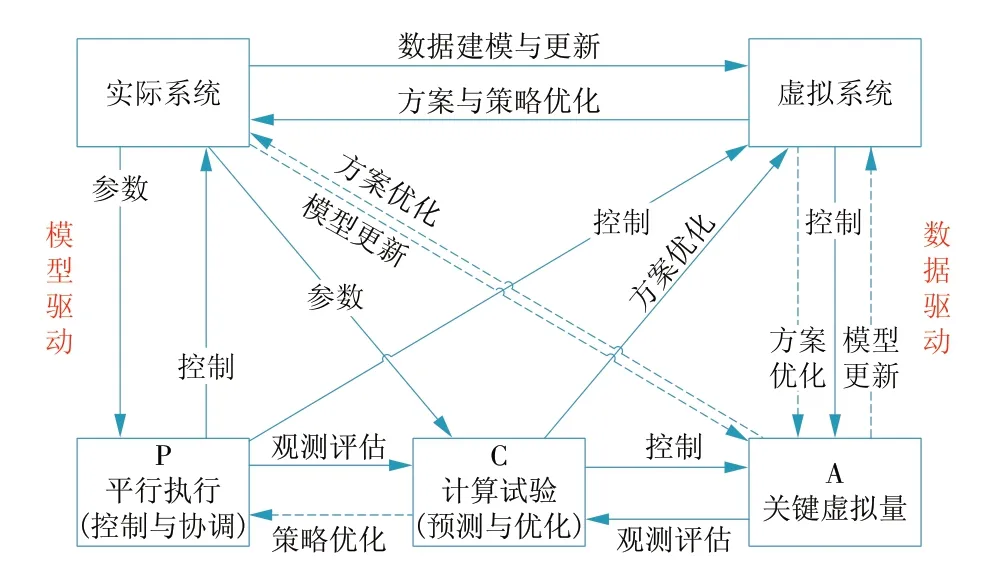
图2 平行系统理论结构关系Fig.2 Structural relations of parallel control theory

CFB 锅炉内部反应十分复杂，传统的机理建模很难实现对床温的精准预测，因此很难构建基于床温参数的虚拟系统。通过深度学习对床温参数进行建模，从而实现从实际系统到虚拟系统的跨越。本文主要研究平行控制的虚拟系统构建及计算试验。虚拟系统通过采集实际系统的数据构建出精准的预测模型，为进一步的优化控制及虚拟量构建奠定基础。

2 模型算法概述

2.1 TPA-LSTM 模型

虚拟系统的构建采用TPA-LSTM 模型，TPALSTM 模型由2部分组成：前一部分为长短期记忆神经网络（LSTM）模型，后一部分为时序关注层。模型输入首先通过LSTM 模型进行计算，接着进入时序关注层，时序关注层的输出为最终的模型输出。

LSTM 模型由Hochreiter 与Schmidhuber 在1997年提出［14］。图3展示了LSTM 模型的细胞结构，模型的核心为细胞状态ct。

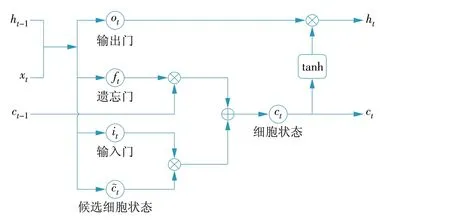
图3 LSTM 细胞结构Fig.3 LSTM cell structure

LSTM模型的计算过程为：当前时刻的输入xt与上一时刻的细胞输出ht-1进行结合，形成LSTM 模型的细胞输入；细胞输入经过权重变换形成遗忘门ft、输入门it、输出门ot及细胞候选状态c～t［15］。

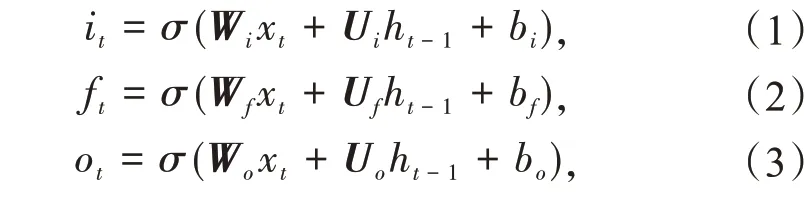
在LSTM 模型中，ht-1的不断传递形成了循环神经网络的一大重要特征——记忆功能。LSTM 神经网络通过遗忘门对细胞中存储的记忆进行选择，实现了LSTM 神经网络的遗忘机制，大大提高了模型效率，由此避免了循环神经网络的“长期依赖”问题。

除了LSTM 神经网络，注意力机制也引起了研究者们的兴趣［16］。注意力机制是在模型中构建关键向量、值向量以及查询向量，通过关键向量与查询向量之间的相似度得分对值向量进行选择，由此提高模型的计算效率和预测精度。TPA-LSTM 最早由Shih 等于2019 年提出［17］。Shih 等使用一组滤波器来提取数据的时序信息，类似于将时间序列数据转换为“频域”，然后提出采用一种新的注意力机制来选择相关时间序列并利用其“频域”信息进行预测。TPA-LSTM 模型注意力机制计算过程如图4 所示（图中：hi为不同特征变量在i时刻的值）。时序关注层的输入为LSTM 神经网络的输出。利用一维卷积对时间序列进行过滤，类似提取“频域”信息。将同一个特征变量的不同卷积核提取出的“频域”信息作为注意力机制中的关键向量及值向量，将最后一个时刻的LSTM 模型输出ht作为查询向量进行注意力机制的计算。最终的结果vt同ht一起形成模型最终的输出。

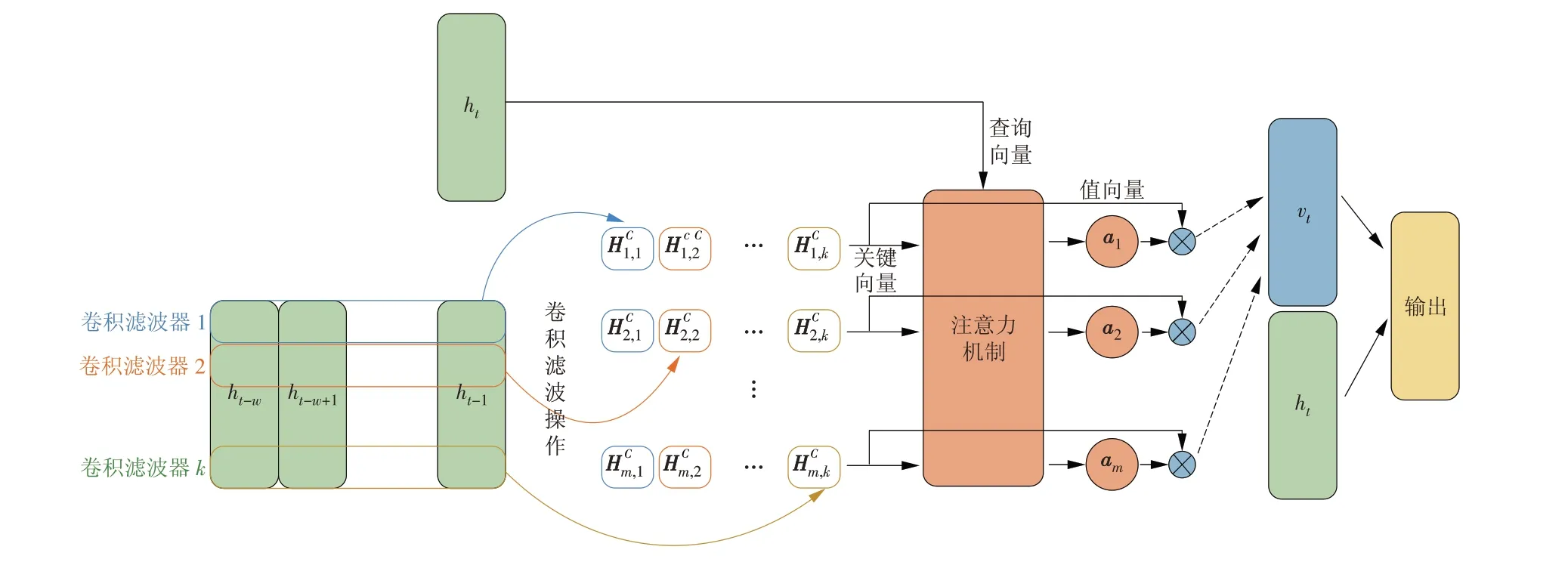
图4 TPA-LSTM 模型注意力机制计算过程Fig.4 Calculation results of TPA-LSTM model attention mechanism

TPA-LSTM 神经网络是在传统的LSTM 神经网络层之后加入了时序注意力机制。为了便于陈述，本文定义以下变量：H为LSTM 层的输出，H的行向量代表同一个特征在不同时间步上的时序，列向量表示在同一时间步上的m个特征值。

首先对H矩阵进行一维卷积操作，得到HC矩阵，其中卷积核的尺度为1×d（d为任务所需关注时序段的最大长度）；卷积操作之后将数据在时序方向进行加权和操作，由于卷积操作的卷积核数量为k，因此每个特征会生成k个不同的卷积结果；单一特征变量利用生成的不同卷积核滤波结果进行关注度计算，最终根据关注度对滤波结果进行加权求和，计算过程如下。

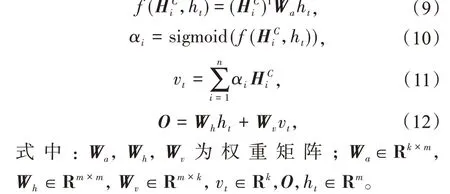
通过以上计算，利用卷积滤波提取时序数据中的时序信息，再根据计算所得的关注度选择与时序部分最后时刻的状态ht类似的数据信息，从而提高模型的预测精度。

2.2 灰色关联度分析法

在虚拟系统构建过程中，需要对实际系统的数据进行筛选，避免冗余变量对模型预测产生影响，从而提高虚拟系统计算试验的准确性。床温受多个参数的影响，这些参数之间存在不同的时滞和相互作用，床温与所有相互作用参数之间的关系就像一个灰色系统。灰色关联分析法（GRA）是由Deng［18］提出的一种根据数据曲线的相似度来度量多个性能之间相互关联度的有效统计方法，本文采取GRA 法来选择模型的输入，其中灰色关联度（GRG）表示参考序列与可比性序列之间相关性的数值度量，该值越接近1，说明2 个序列之间的重合程度越高。灰色关联度分析的主要步骤如下。

（1）首先，将目标序列和比较序列进行标准化处理，本文采用最大最小归一化方式。

2.3 性能评价指标

为了评估不同试验场景下的预测性能，选择多种科学性能指标进行时间序列预测。本文用平均绝对误差EMA、平均绝对百分比误差EMAP评估不同模型的性能。

平均绝对误差

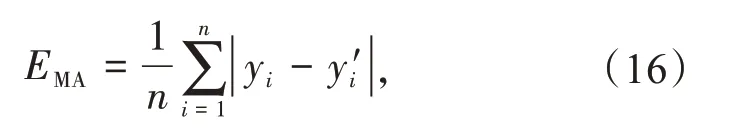
平均绝对百分比误差

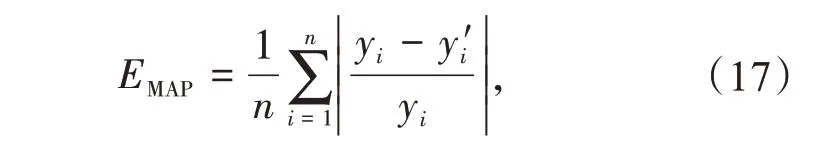
式中：y′i为预测模型的预测值；n为预测数据的数量；yˉ为实际值的平均值。

通常情况下，EMA和EMAP值越低，表示预测精度越高。

3 实例分析

3.1 数据集划分

以某330 MW 循环流化床机组的生产数据为例，说明预测建模步骤。本文的预测方法以20 s 后左侧床温为预测目标，以历史采样数据作为模型的输入数据。数据均来自现场分散控制系统（DCS），数据采样间隔为5 s，数据数量为42 000。数据集按照37 800，1 600，2 600 的数据段依次分为训练集、验证集、测试集。以负荷为例，图5展示了数据集划分的结果。其中，数据集1，2，3分别表示训练集、验证集和测试集。由图5 可知，机组大部分时间处于变负荷阶段，因此采用传统的建模方法很难实现对床温的精准预测，因此本文采用深度神经网络模型对床温进行预测。需要注意的是，整个采样期间，煤质并未发生明显变化，因此本文的模型并未考虑煤质对床温的影响。

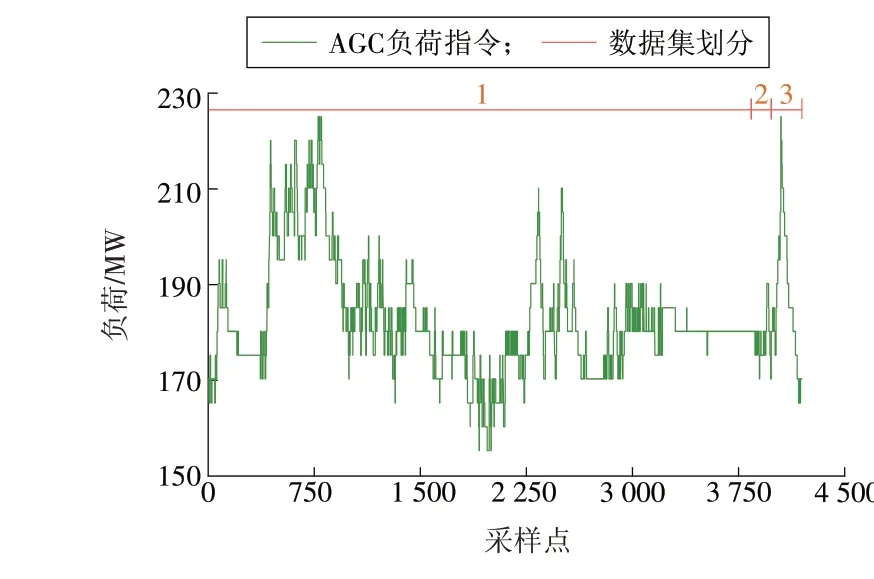
图5 数据集划分Fig.5 Data set partitioning

3.2 变量筛选及模型超参数选择

在虚拟系统构建过程中，本文对输入变量进行了灰色关联度分析。为了便于展示结果，本文将输入变量进行编号，见表1（表中，AGC 为自动发电控制）。灰色关联度分析结果如图6所示。

图6 灰色关联度分析结果Fig.6 Results of grey correlation degree analysis

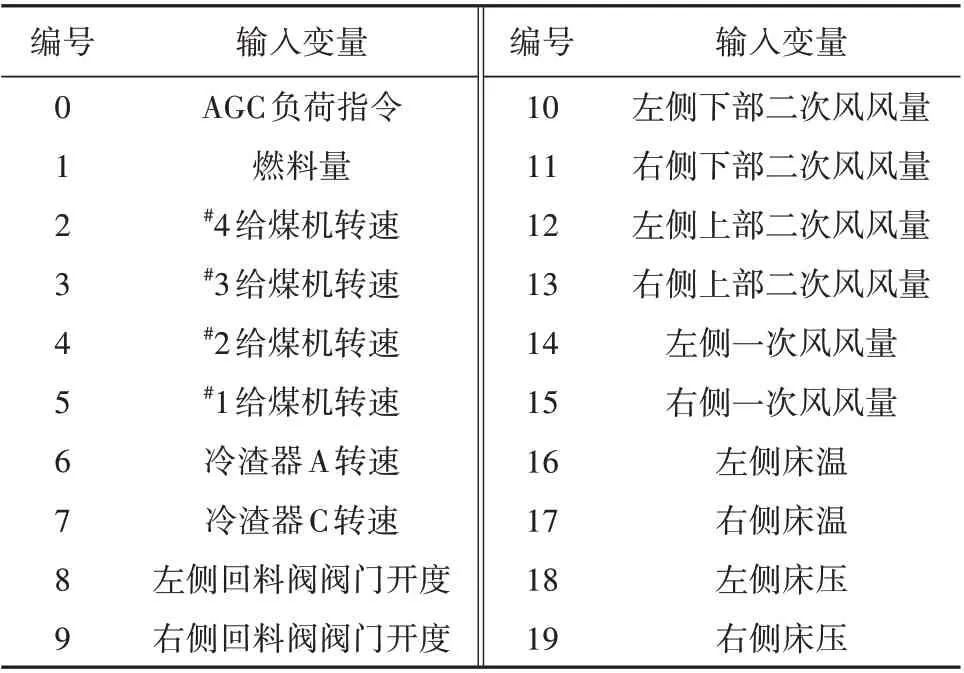
表1 输入变量编号Table 1 Numbering for the input variants

以左侧床温为例进行预测。设置灰色关联度阈值为0.7，根据灰色关联度分析结果选择模型的输入变量为#4 给煤机转速、#3 给煤机转速、#2 给煤机转速、#1 给煤机转速、左侧一次风风量、右侧床温及右侧床压。需要注意的是，为了减少目标变量自相关性的影响，本文采用床温的一阶差分预测法，计算方法如下

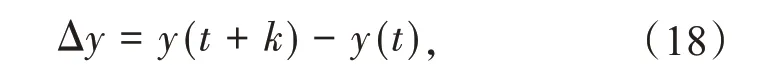
式中：y(t+k)为预测目标在t+k时刻的值；y(t)为预测目标在t时刻的值；Δy为2个时刻的差值。

本文采用TPA-LSTM 模型对炉膛左侧床温进行预测。通过训练集对模型参数进行训练，并采用验证集进行模型超参数选择。模型训练的损失函数采用MAE，采用Adam［19］优化器进行训练。模型的超参数选择结果见表2。

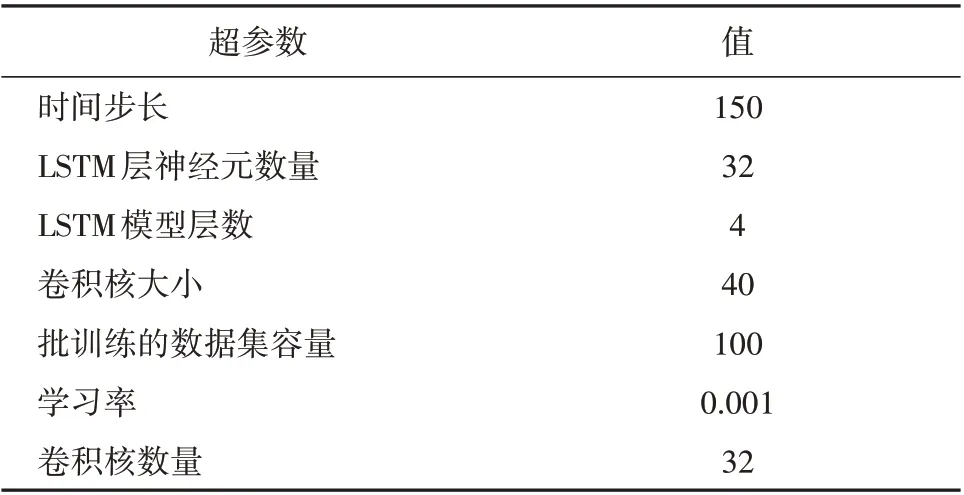
表2 模型超参数选择结果Table 2 Hyperparameter selection for the models

3.3 模型预测结果

利用训练好的模型对测试集数据进行预测，预测结果如图7所示（图7a为测试集的全部预测结果，图7b—图7h 为局部放大后的细节图）。采用EMA，EMAP对预测结果进行评价，其中，预测性能的真实值采用20 s 后的床温测量值，评价结果显示：EMA=0.131 7 ℃，EMAP=0.014 29%。从评价结果可见，本文构建的预测模型能够很好地对床温进行建模并提前预测床温。这种精准的预测结果可为平行控制系统中的平行执行及关键虚拟量构建奠定研究基础，实现虚拟系统对实际系统的优化和指导。

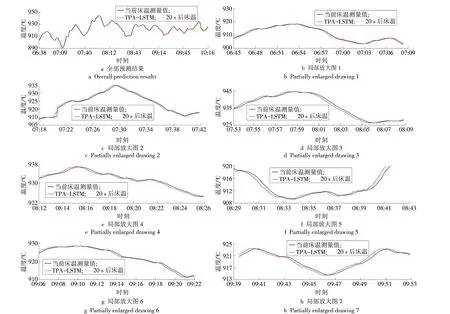
图7 TPA-LSTM 模型预测结果Fig.7 Prediction results of the TPA-LSTM model

3.4 模型预测性能对比

为了验证本文所提出预测算法的优势，将TPA-LSTM 模型与传统的LSTM 模型进行对比。2个模型均采用相同的输入变量。为了更好地展示对比效果，采用20 s后的床温值作为真实值，对比结果如图8 所示（图8a 为测试集的全部预测结果，图8b—图8h为局部放大后的细节图）。

图8 不同模型预测结果对比Fig.8 Prediction results of different models

采用EMA，EMAP指标对2 种模型的预测结果进行评价，预测性能对比见表3。从对比结果可以看出，本文提出的TPA-LSTM 预测模型能够更准确地对床温进行预测，预测性能相较于LSTM 神经网络模型有一定提升。实际工业过程中，系统运行数据通常存在不同程度的滞后，传统的LSTM 模型仅考虑了时序数据的前后关联；同时，LSTM 模型的遗忘机制并不能很好地选择最佳的时序段，本文通过加入时序关注模式，使得模型能够选取最有效的时序段对目标变量进行建模和预测。

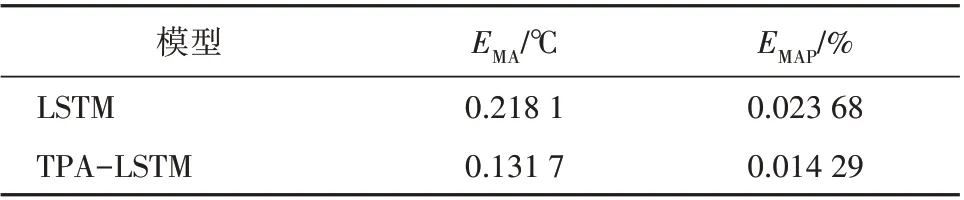
表3 模型预测性能对比Table 3 Performance comparison of the forecast models

3.5 平行控制应用展望

本文的主要研究针对平行控制的虚拟系统构建及计算试验。利用历史数据结合预测模型构建床温参数的虚拟系统，以实现对床温的预测；将预测值实时反馈给现场运行人员，现场运行人员通过判断对机组运行进行适当调整，实现虚拟系统对实际系统的指导作用；虚拟系统源源不断地从实际系统获取数据，对模型结构、参数进行调整；虚拟系统的预测结果将为实际系统的运行提供指导和优化，从而实现虚拟系统与实际系统之间的交互。

后续的平行控制应用研究将结合预测模型实现对机组运行参数的优化，以最佳床温运行范围为主要优化目标，以控制量（如#4 给煤机转速、#3 给煤机转速、#2给煤机转速、#1给煤机转速以及左侧一次风风量）为优化对象，中间量（如右侧床温和右侧床压）需要保持与当前时刻测点数据一致。通过优化结果对机组的运行策略进行调整，采用启发式优化算法对控制量进行寻优，实现虚拟系统对实际系统的优化。

尽管给出了具体的实施方法，但在目前的运行中仍存在以下问题。（1）程序计算时间过长，无法对机组进行实时控制调整。尽管通过优化计算机硬件可以适当缩短计算时间，但其根源在于优化算法的计算量过大。（2）模型输入中非控制量的约束问题，如将右侧床温及右侧床压固定为当前时刻的测量值，如何针对非控制量进行约束是一个亟须解决的问题，希望后续的研究能在这些方面有所突破，实现由虚拟系统到实际系统的优化。

4 结束语

在平行控制的理论背景下，本文针对循环流化床的床温参数进行了虚拟系统构建和计算试验，实现了对床温的精准预测。通过灰色关联度对模型输入进行了筛选，利用TPA-LSTM 模型对床温值进行预测，取得了精准的预测结果。本文的预测模型可为变负荷工况下的机组控制策略提供参考。与LSTM 模型进行对比，本文的预测模型的预测性能有一定提升。尽管本文的模型取得了非常好的预测效果，但本文的研究并未考虑煤质变化对模型预测效果的影响，今后会在这一方面进行深入研究。

后续将对计算试验与平行执行、关键虚拟量构建之间的互动关系展开研究，为发电机组智能平行控制理论的应用奠定基础。