基于有限元分析的大型核电汽轮机轴系中心偏差的影响分析

姜海涛

（辽宁红沿河核电有限公司，辽宁大连 116319）

0 前言

由于核电站蒸汽参数较低，电功率较大，汽轮机需要大流量的蒸汽，所以汽轮机的排汽面积设计得较大，末级叶片较长，核电汽轮机体积较火电汽轮机更大［1-5］。同时，为降低离心力作用，通常采用半速汽轮机。本文所述的汽轮机组为功率1 120 MW 的核电半速汽轮机。

汽轮发电机通常由多个转子组成，各个转子用联轴器连接起来，构成一个多支点的转子系统，统称为轴系。轴系找中心的目的在于使各个转子的中心线在一条平滑的轴线上［6-9］。良好的轴系中心状态可以限制各个轴瓦的负荷，从而防止振动增大和轴瓦过载，并且控制交变弯曲应力在一个低的水平，从而限制疲劳，防止缺陷发展［10-11］。

汽轮机运行时，由于基础沉降、轴承钨金磨损、轴承座位移等因素，汽轮机轴系中心会发生变化，所以在检修时要对汽轮机组中心进行重新调整［12-13］。然而在实际检修过程中，我们发现轴系中心在调整前的偏差曾达到0.60 mm 以上，远超设计要求的0.02 mm，但是轴瓦和转子在上一个周期的运行状态良好，且轴瓦的解体检查情况也良好。本文拟通过定量分析，确定轴系中心的偏差具体会产生哪些影响。

1 汽轮机结构介绍

某核电百万千瓦汽轮发电机组为单轴半速机组，由1 个高中压合缸、3 个低压缸和1 个发电机组成，总共5 根转子，每根转子由2 个轴承支撑。相邻的转子通过刚性联轴器连接，总计10 个支撑轴承、4 组联轴器，整个轴系长度约66 m。

其中支撑轴瓦为三可倾瓦结构，每个轴承包括主要承载的底瓦、辅助承载的侧瓦和限制向上位移的顶瓦。联轴器由液压对轮螺栓紧固，每对联轴器均匀分布有16 个螺栓孔，螺栓与联轴器螺栓孔形成过盈配合。过盈配合保持了联轴器的同心度，保证各个联轴器精确的刚性耦合。

2 汽轮机轴系找中心理论

汽轮机轴系找中心的原理是使一个转子中心线与另一个转子中心线重合，使之成为一条连续的曲线，从而保证各转子通过联轴器形成一根连续的轴，通过测量相邻联轴器的外圆和张口来保证联轴器对中。完全对中的联轴器在紧固后应保证无垂直和水平方向的应力，联轴器螺栓仅在轴向上受拉力，从而保证联轴器端面有足够大的摩擦力来承载旋转扭矩。

2.1 单个转子的静挠度曲线

汽轮机转子重量大、跨距大，为挠性转子，在重力的作用下会发生挠性弯曲。对低压转子进行建模和有限元计算，叶片未进行建模，按照重力加载。轴瓦和转子的接触面按照无穿透接触单元处理，设置摩擦。轴承底部为球面垫铁支撑，可自由旋转，接触面按照无穿透接触单元设置。垫铁底部进行固定约束设置。网格模型采用四面体单元，单元总数432 246 个，节总数662 308 个，对于结构突变区域进行局部细化。

计算结果表明转子在重力作用下以轴承支撑位置为基准点，联轴器向上位移，最大值为0.39 mm；转子中心位置向下位移，最大值为0.52 mm。在变形后的转子上取点，绘制低压转子在重力下的挠度曲线如图1 所示，变形后的转子为一条光滑的挠度曲线。

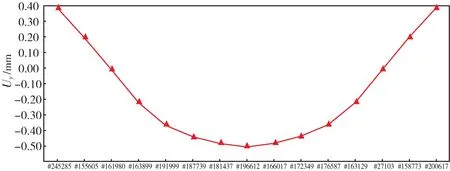
图1 低压转子在重力下的挠度曲线Fig.1 Deflection curve of low pressure rotor under gravity

2.2 轴系找中心原理

根据转子在重力下的形变图可知，转子在重力的作用下形成一个弯曲的挠度曲线，联轴器上移，联轴器端面除了在上下方向的位移外，联轴器上下位置在轴向上会产生大小不一的位移量［6，8-9］。为保证多个转子成为一条连续的曲线，需要调整轴承的标高，根据计算，对于双转子，当前后端的轴承标高为1.99 mm 时，联轴器处张口为0，整个轴系能够成为一条光滑的挠度曲线，如图2 所示。

图2 轴系的挠度曲线Fig.2 Deflection curve of shafting

2.3 轴系找中心调整计算

一般中心偏差会出现3 种情况：（1）端面平行但中心不重合；（2）端面不平行中心重合；（3）端面不平行且中心不重合［10］。实际汽轮机检修中经常出现第三种情况。

汽轮发电机组轴系共有4 组对轮，找中心后需保证每一组对轮的中心偏差在标准范围内。先将其进行简化，对一组对轮进行分析，如图3 所示。

由相似三角形得出：b/c=d/CE；b/e=d/CE；a/c=AE/CE；a/e=AC/EC。其中，b为平面偏差（平面张口）；a为圆周偏差（圆周错口）。

根据以上关系，即可计算如图3 所示的中心偏差为a（圆周偏差）和b（平面偏差）时，支承C和E的调整量c和e为：

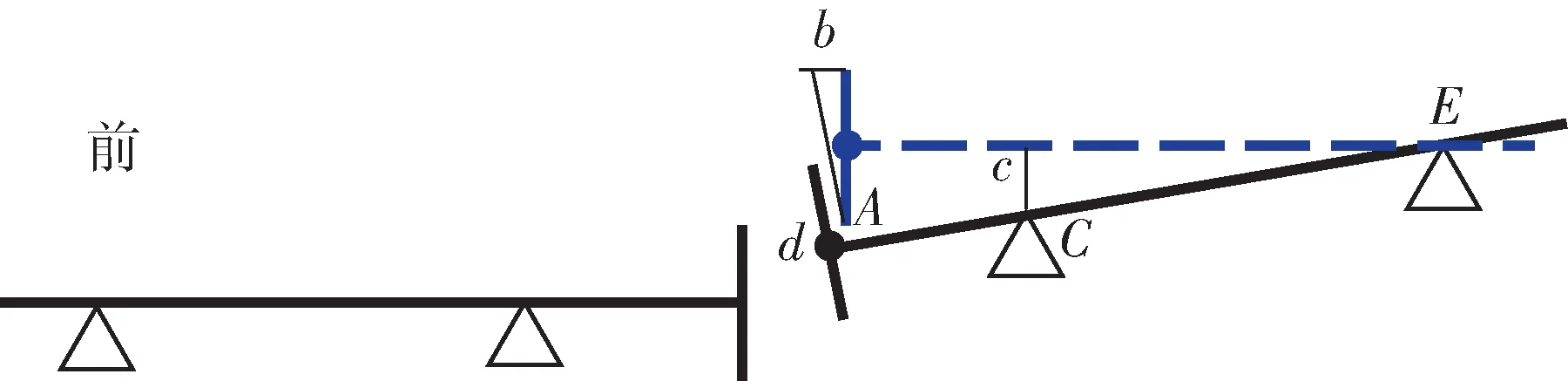
图3 中心偏差图Fig.3 Center deviation diagram

计算结果中若c、e为正值，表示需抬高；若c、e为负值，表示需下调。

以某弹性基础的汽轮机轴系为例，如图4 所示。选取4#和5#对轮进行计算，如调整4#、5#号对轮偏差，可通过对3#、4#、5#、6#轴承（低压缸）及Ⅲ弹簧基础进行调整。

图4 中e1、e2、e3、e4为3#、4#、5#、6#地脚调整量、转子直径为d、初始中心为a1、初始张口为b1、调整后的中心为a′1、张口b′1、弹簧Ⅲ调整量为f。

图4 轴系中心计算模型Fig.4 Calculation model of shafting center

调整完e1、e2、e3、e4及弹簧f后的张口和同心度为：

3 轴系中心偏差的影响

联轴器中心的外圆和张口偏差通过联轴器螺栓虽然可以消除，但是联轴器会发生变形，从而产生应力，在转子高速旋转下会发生交变应力，导致联轴器部件发生疲劳。另外中心偏差也会对轴瓦载荷产生影响，偏高的转子负荷增加，导致瓦温升高，同时偏低的转子负荷减少，会使轴承接触不良造成振动上涨或上部轴瓦磨损。通过计算不同外圆和张口偏差下，轴系的轴瓦载荷和转子应力，确定轴系中心偏差的影响。

3.1 模型建立

以两个低压转子连接的轴系为例，进行建模和有限元计算，叶片未进行建模，按照重力加载。轴瓦和转子的接触面按照无穿透接触单元处理，设置摩擦。由于联轴器为刚性连接，两个联轴器的接触面按照接合单元处理。4 个轴承的底部为球面垫铁支撑，可自由旋转，接触面按照接触无穿透单元设置。网格模型采用四面体单元，单元总数884 679 个，节总数1 351 806 个，对于结构突变区域进行局部细化。整个模型设置重力载荷，根据不同的张口和外圆偏差对垫铁底部进行位移约束设置。

采用四面体单元，有4 个节点，单元的节点位移有12 个自由度，因此每个方向的位移场可以设定4 个待定系数，根据节点个数以及确定位移模式的基本原则，选取该单元的位移模式为：

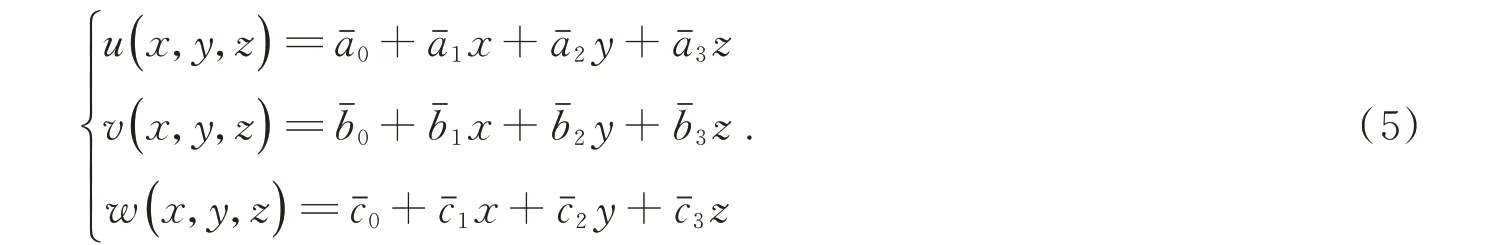
在材料的弹性区域之内，应力和应变之间存在一定的关系，即满足胡克定律，这个关系可以用下列方程式表示：

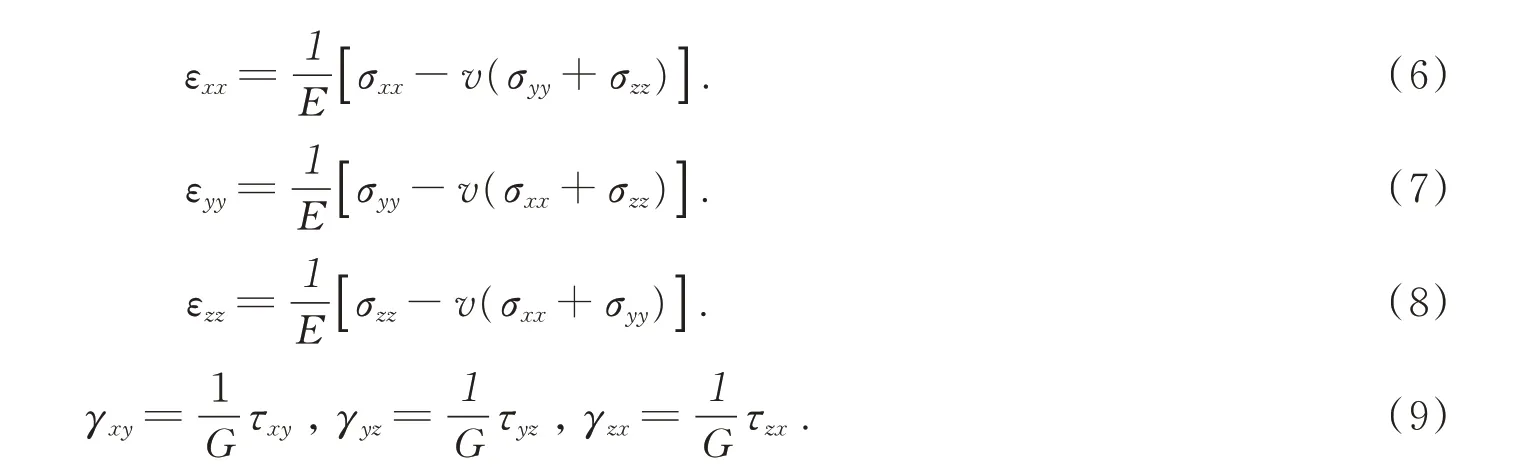
3.2 上下外圆偏差的影响

两个转子按照前后顺序分别编号为LP1 和LP2，轴承按照前后顺序编号为1#—4#轴承，分别设置外圆上下偏差0 mm、0.1 mm、0.2 mm、0.3 mm、0.4 mm、0.5 mm、0.6 mm 总计7 个状态进行有限元计算，得到的底瓦和侧瓦的载荷及联轴器的等效应力值进行处理，绘制曲线，如图5—图7 所示，由此得出以下结论：

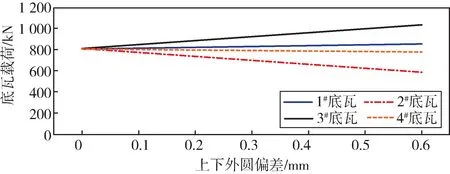
图5 上下外圆偏差与底瓦载荷的关系曲线Fig.5 Relation curve between upper and lower outer circle deviation and bottom pad load

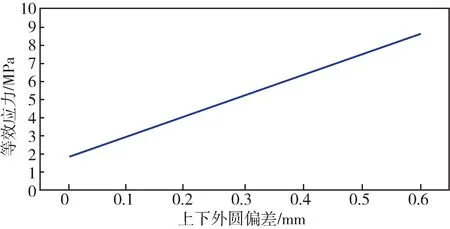
图7 上下外圆偏差与等效应力的关系曲线Fig.7 Relation curve between upper and lower cylindrical deviation and equivalent stress

外圆偏上的联轴器，紧固后对应的轴瓦载荷更大，外圆偏下的联轴器对应的轴瓦载荷更小。随着LP2 外圆的升高，2#底瓦和2#侧瓦的载荷明显减小，3#底瓦和3#侧瓦的载荷明显增加，整体趋势呈线性分布。

外圆偏差对相邻轴瓦的载荷影响较大，对外部的1#、4#轴瓦影响较小。当外圆偏差达到0.6 mm 时，对2#、3#底瓦和侧瓦载荷的影响约27%；对1#、4#底瓦和侧瓦载荷的影响约4.5%。

随着外圆偏差的增大，等效应力值不断增大，联轴器应力最大值在轴瓦与转子接触的承载面附近，如图8 所示。

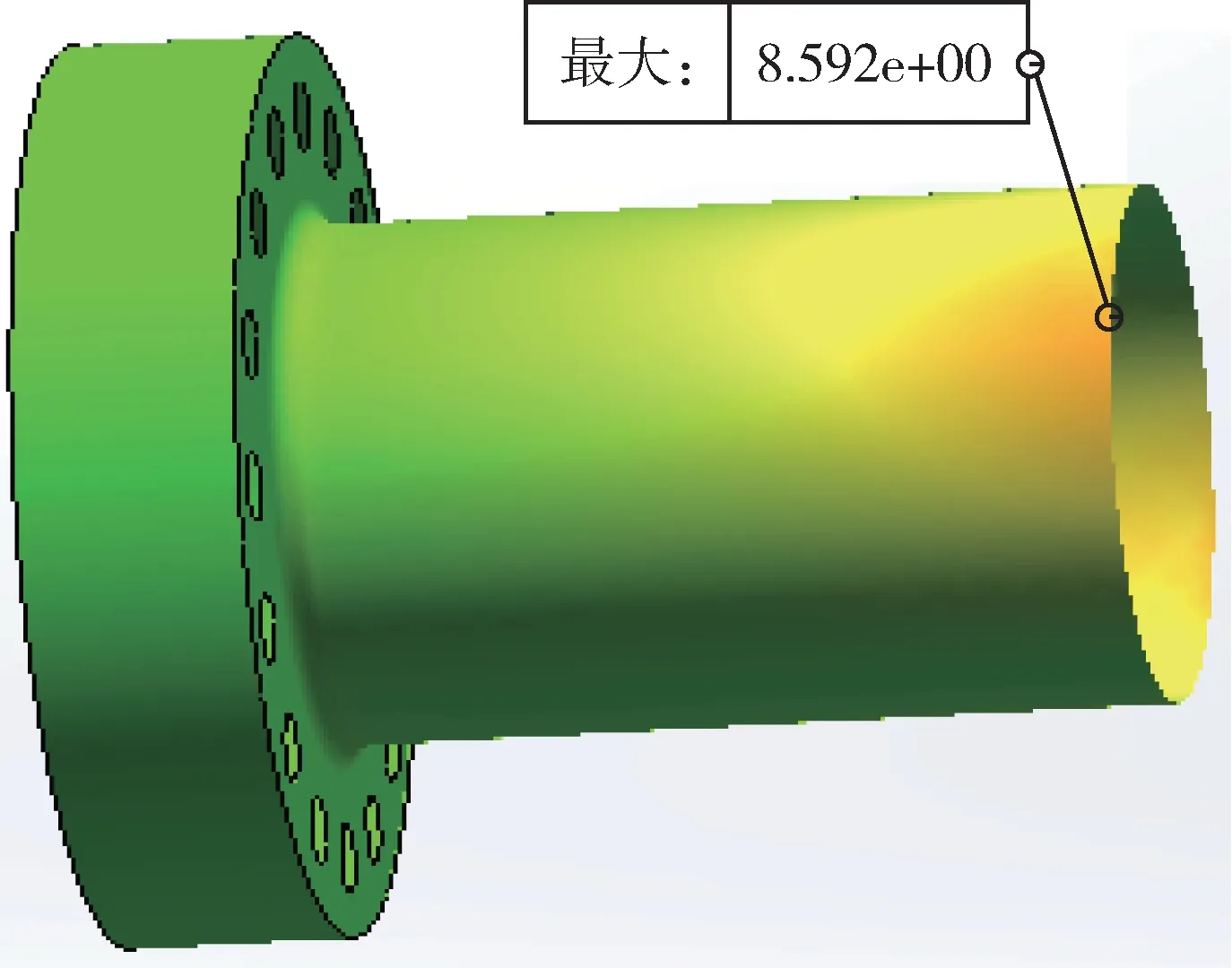
图8 上下外圆偏差对应力的影响Fig.8 Influence of upper and lower cylindrical deviation on stress

图6 上下外圆偏差与侧瓦载荷的关系曲线Fig.6 Relation curve between upper and lower outer circle deviation and side pad load

3.3 左右外圆偏差的影响

同3.2 节设置7 个状态进行有限元计算，同时向左侧移动3#、4#轴承，得到的底瓦和侧瓦的载荷及联轴器的等效应力值进行处理，绘制曲线，如图9—图11 所示。由此可以得出以下结论：

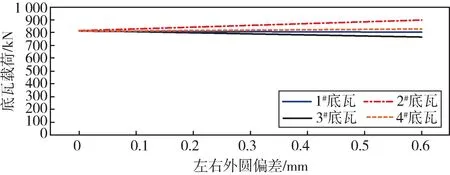
图9 左右外圆偏差与底瓦载荷的关系曲线Fig.9 Relation curve between left and right outer circle deviation and bottom pad load

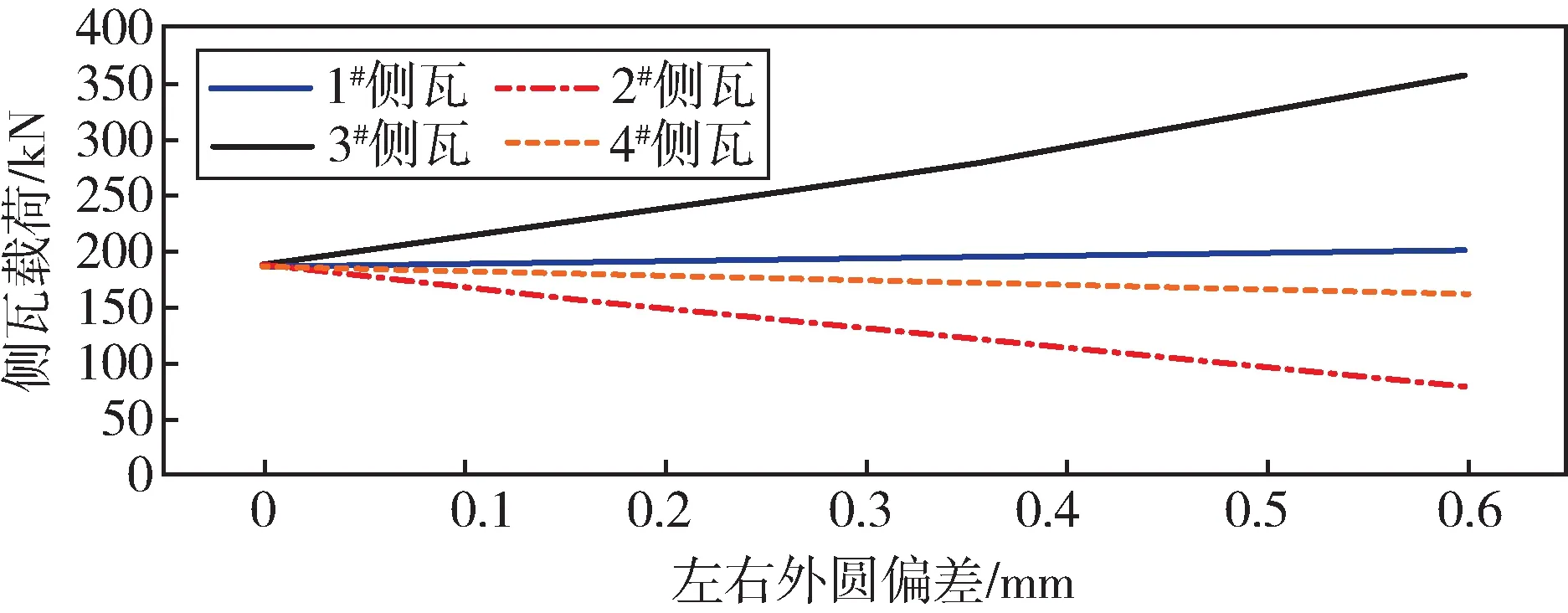
图10 左右外圆偏差与侧瓦载荷的关系曲线Fig.10 Relation curve between left and right outer circle deviation and side pad load

图11 左右外圆偏差与等效应力的关系曲线Fig.11 Relation curve between left and right outer circle deviation and equivalent stress

随着左右外圆偏差的增大，底瓦和侧瓦的载荷偏差逐渐增大，整体趋势呈线性分布。外圆偏差对相邻轴瓦的载荷影响较大，对外部的1#、4#轴瓦影响较小。对侧瓦载荷的影响较大，对底瓦载荷的影响相对较小。当外圆偏差达到0.6 mm 时，2#、3#侧瓦的最大载荷增加了将近一倍，而2#、3#底瓦的最大载荷增加了10%左右。对1#、4#底瓦载荷的影响为1.6%左右，基本未产生影响，对1#、4#侧瓦的最大影响为12%左右。随着外圆偏差的增大，等效应力值不断增大，联轴器应力最大值在轴瓦与转子接触的承载面附近，如图12 所示。

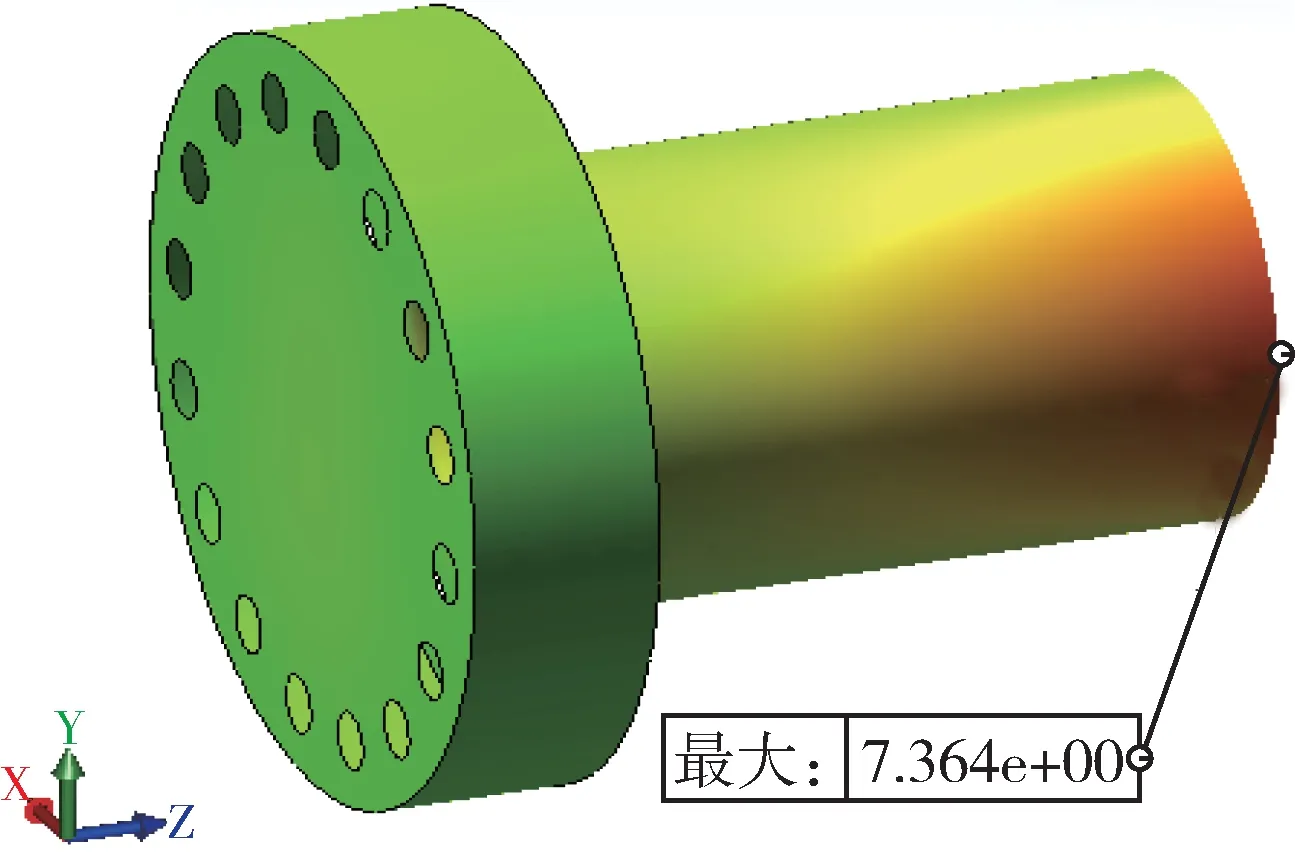
图12 左右外圆偏差对应力的影响Fig.12 Influence of left and right outer circle deviation on stress

3.4 上下张口偏差的影响

分别设置上下张口偏差-0.3 mm、-0.2 mm、-0.1 mm、0 mm、0.1 mm、0.2 mm、0.3 mm 总计7 个状态进行有限元计算，对计算的数据进行处理，绘制曲线，如图13—图15 所示。由此可以得出以下结论：

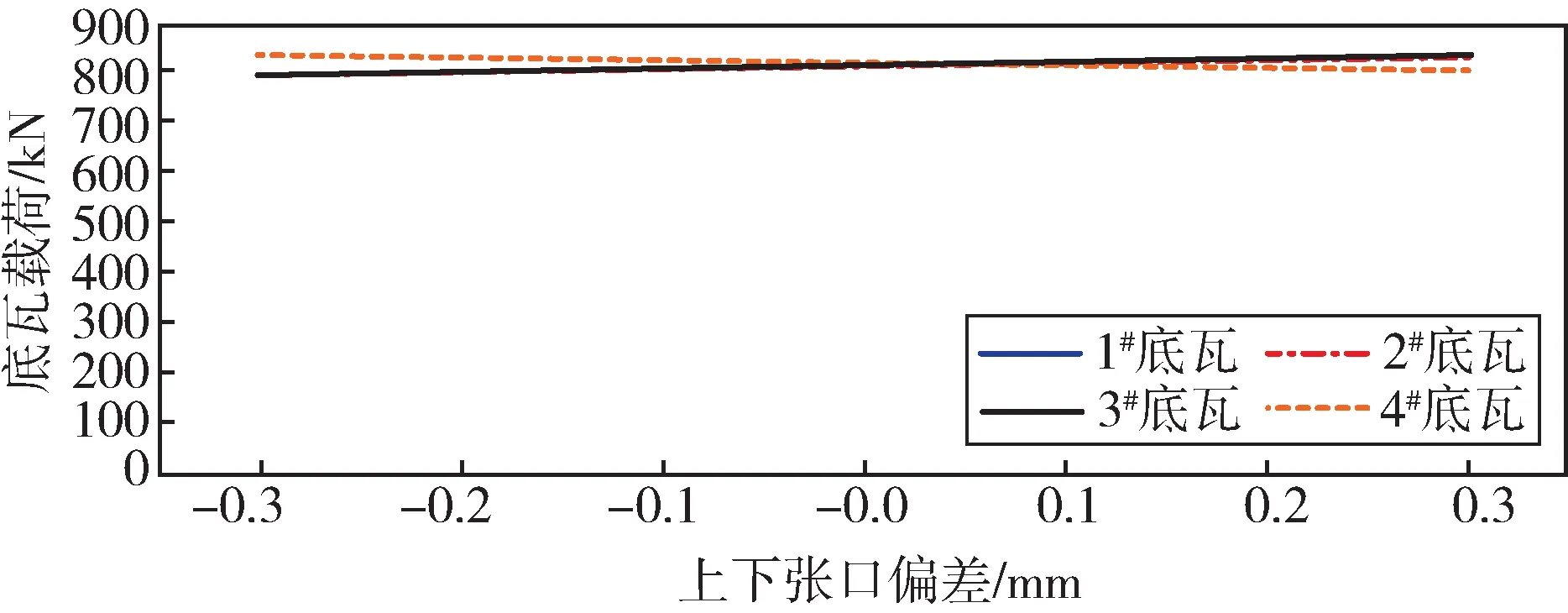
图13 上下张口偏差与底瓦载荷的关系曲线Fig.13 Relation curve between upper and lower opening deviation and bottom pad load

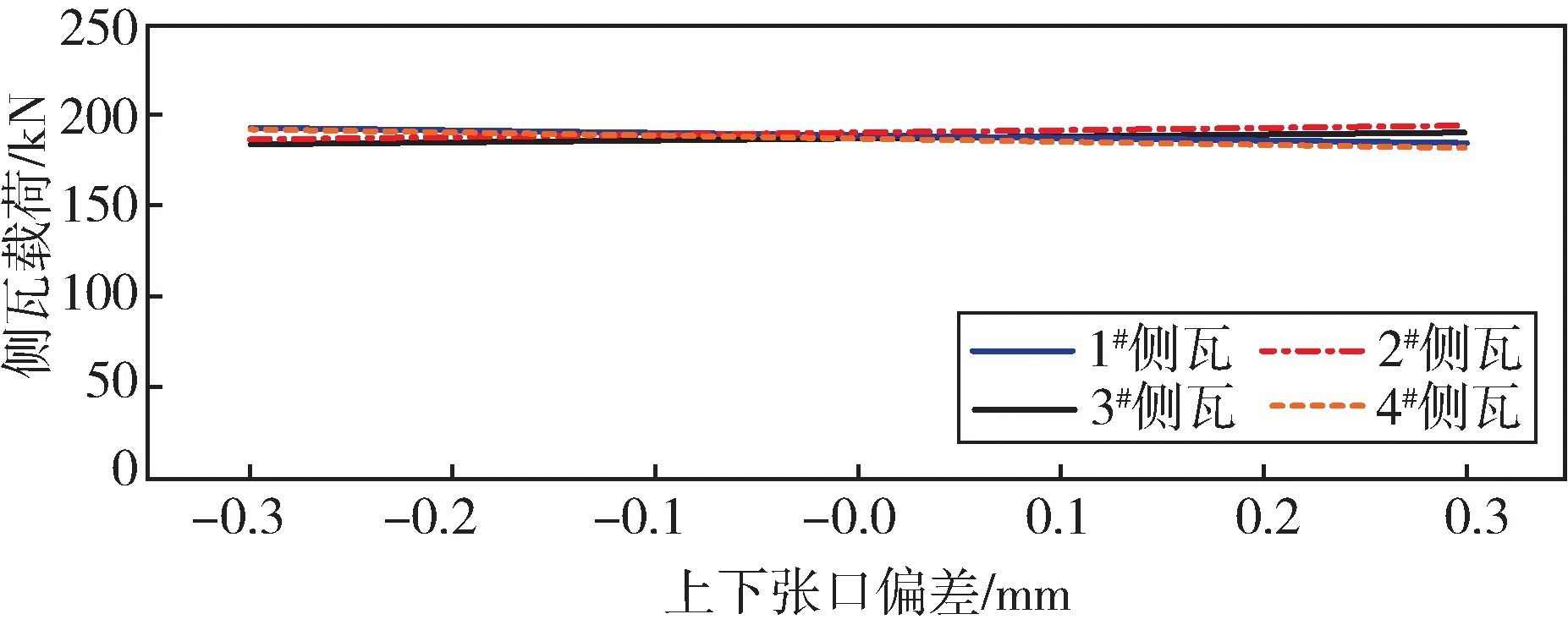
图14 上下张口偏差与侧瓦载荷的关系曲线Fig.14 Relation curve between upper and lower opening deviation and side pad load

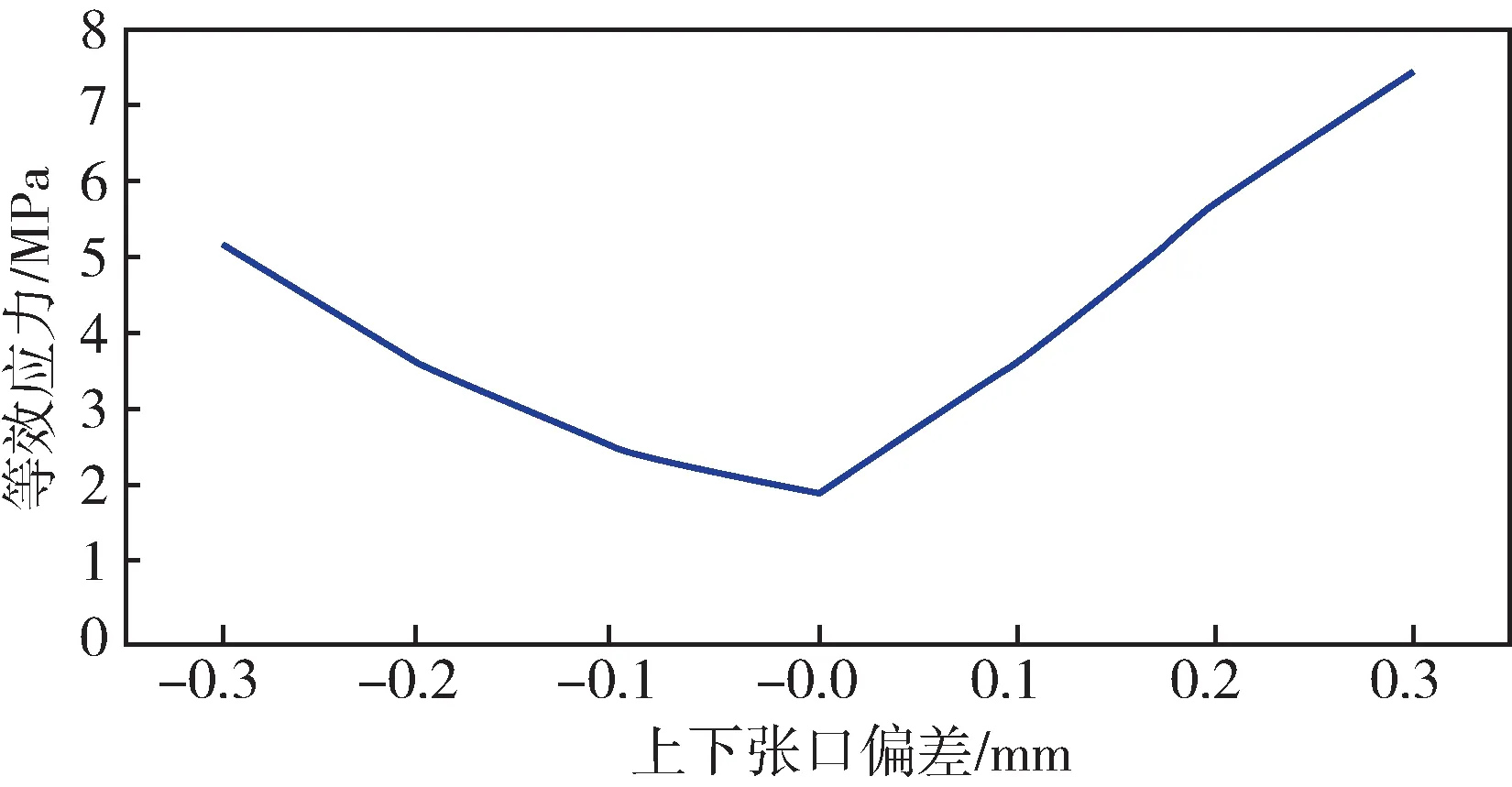
图15 上下张口偏差与等效应力的关系曲线Fig.15 Relation curve between upper and lower opening deviation and equivalent stress

随着上下张口偏差的增大，底瓦和侧瓦的载荷偏差逐渐增大，整体趋势呈线性分布。张口偏差对各个轴瓦载荷的影响基本一致，对相邻轴瓦的载荷影响与外部的1#、4#的轴瓦影响大小一致，方向相反。上张口导致相邻的2#、3#轴承载荷较大，外部的1#、4#轴承载荷变小。对底瓦和侧瓦的载荷影响也基本一致，当张口为0.3 mm 时，偏差范围在2%～3%之间，相对于同样大小的外圆偏差，上下张口偏差对轴瓦载荷的影响明显偏小。随着外圆偏差的增大，等效应力值不断增大，联轴器应力最大值在轴颈和对轮连接处，如图16所示。

图16 上下张口偏差对应力的影响Fig.16 Influence of upper and lower opening deviation on stress

3.5 左右张口偏差的影响

同3.2 节设置7 个状态进行有限元计算，得到的底瓦和侧瓦的载荷及联轴器的等效应力值进行处理，绘制曲线，如图17—图19 所示。由此可以得出以下结论：

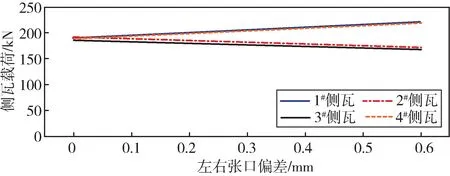
图18 左右张口偏差与侧瓦载荷的关系曲线Fig.18 Relation curve between left and right opening deviation and side pad load

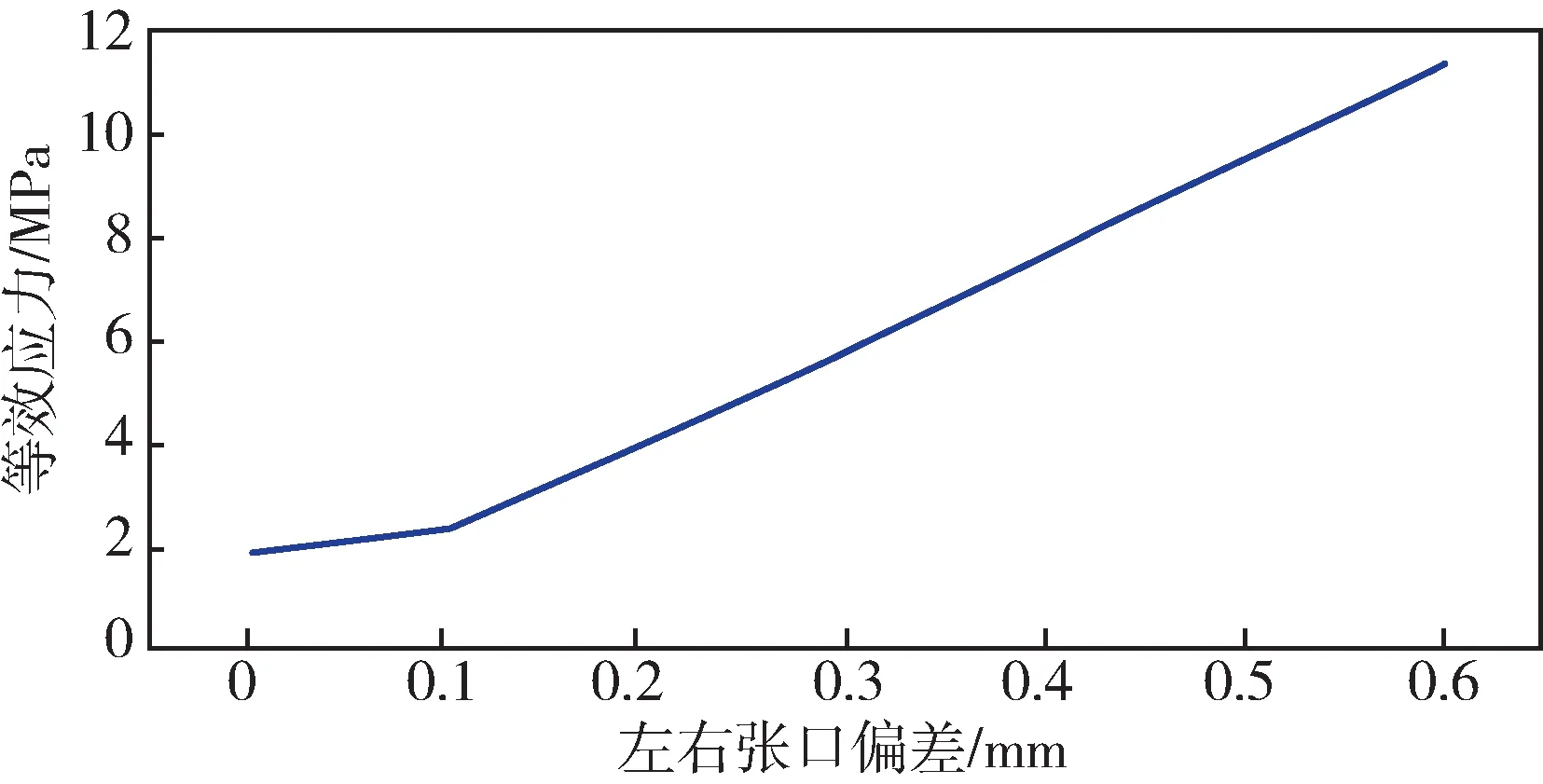
图19 左右张口偏差与等效应力的关系曲线Fig.19 Relation curve between left and right opening deviation and equivalent stress

随着左右张口偏差的增大，底瓦和侧瓦的载荷偏差逐渐增大，整体趋势呈线性分布。张口偏差对各个轴瓦载荷的影响不一致，对相邻轴瓦的载荷影响与外部1#、4#轴瓦的影响方向相反。对侧瓦的影响较大，对底瓦的影响较小。相对于同样大小的外圆偏差，左右张口偏差对轴瓦载荷的影响明显偏小。

随着外圆偏差的增大，等效应力值不断增大，联轴器应力最大值在轴颈和对轮连接处，如图20 所示。

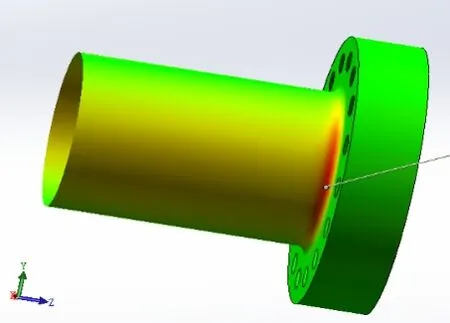
图20 左右张口偏差对应力的影响Fig. 20 Influence of left and right opening deviation on stress

4 检修及运行数据分析

选取某次大修检修前后的轴系中心和轴瓦运行数据，如表1 所示，表中检修前的中心偏差最大值为圆周偏差0.29 mm、平面偏差0.11 mm，调整后的中心偏差均在标准值0.02 mm 以内。查询对应的轴瓦运行参数，检修前后瓦温的最大偏差为1.3 ℃，振动的最大偏差为7.6 μm，检修前后的轴瓦温度和振动值未见明显的变化。检修前的中心偏差值未对轴系的运行状态造成明显影响。

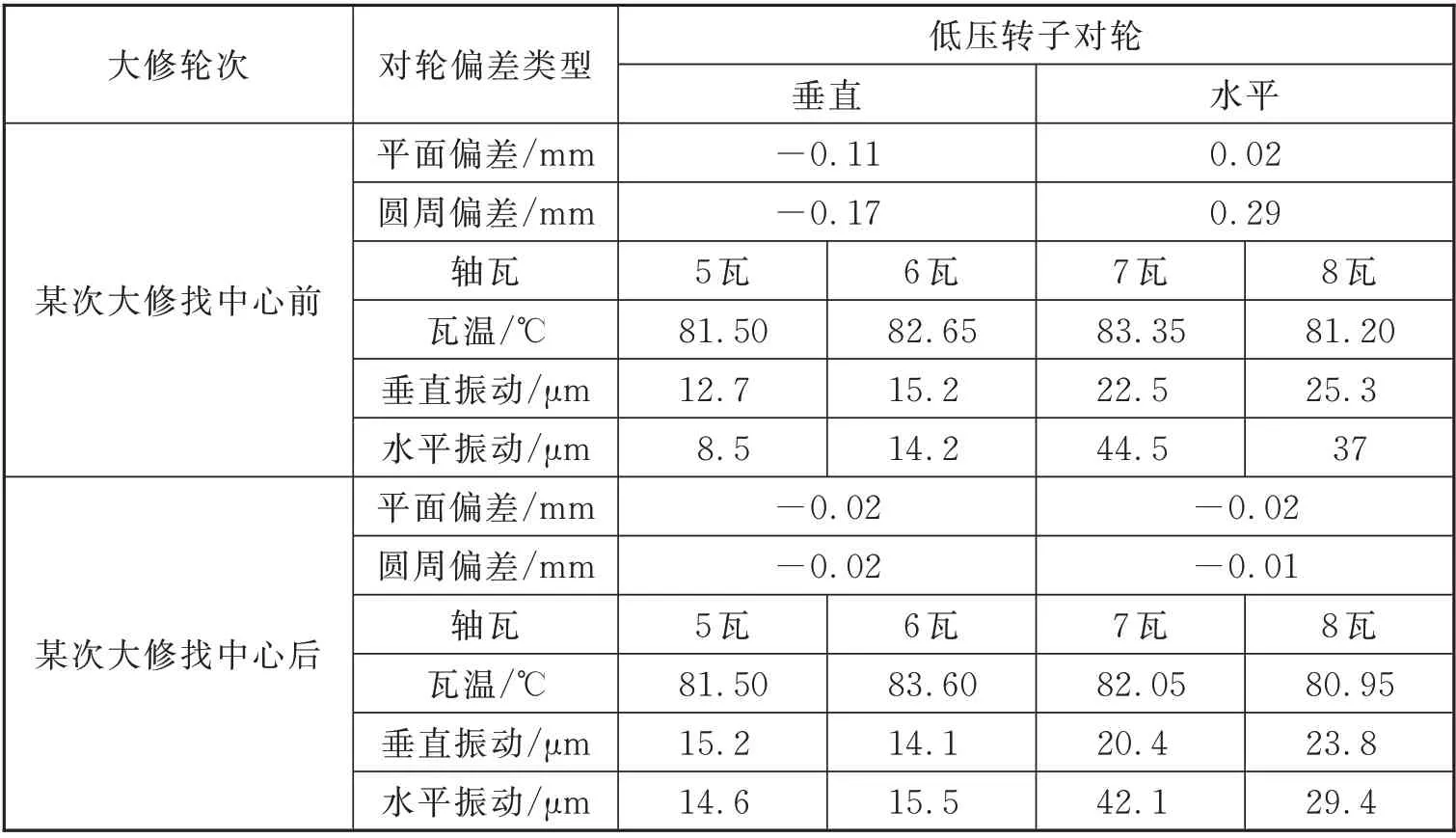
表1 检修前后的轴系中心和运行状态数据Tab.1 Shafting center and operation status data before and after maintenance

5 结论及应用

轴系中心作为影响机组运行状态的关键参数，其标准控制较为严格，通过计算，得到不同的中心偏差对轴瓦载荷和转子应力的影响，过大的中心偏差会导致轴瓦载荷分布不均，从而造成轴瓦温度升高或者轴瓦振动增大。同时过大的中心偏差会显著地增加转子的应力，在转子高速旋转的状态下产生交变应力，增加转子高周疲劳的风险。然而，一定的中心偏差未造成明显的轴瓦温度和振动的上升。

影响轴系中心的因素除了检修之外，还受低压缸真空和温度变化导致的轴承座膨胀、油膜参数、发电机内部气体压力等诸多因素影响。轴系中心调整除了以制造厂的标准要求为基础外，同时需要考虑凝汽器真空度、发电机内部压力等影响；涉及对通流间隙有影响的，还需要结合机组通流间隙调整要求，并参考检修前机组的振动和瓦温状态，结合检修工期要求等因素综合考虑。