基于Simulink的无刷电机模型正弦波信号优越性研究

卢 佳,赵鹏禄,吴 洁,周 洋,马佳兴,高 恺

(江苏大学,江苏 镇江 212013)

0 引言

无刷直流电机是用电子换向器代替传统有刷电机的新型电机。相较于传统有刷电机,它不仅具有质量轻盈、使用寿命长、工作效率高的优点,还具有更高的输出转矩和体积比。因此,无刷直流电机被广泛应用于对电机大小要求较高的场合,如电动摩托车的电机等。这对于无刷电机的稳定性以及可靠性研究极具现实意义。

1 国内外研究现状

根据宋煜[1]研究表明:在对正弦波和方波驱动的研究中,发现方波驱动可以减少20%转矩脉动;通过控制相电压,使相电压尽可能靠近正弦波,可将转矩脉动从14%降低到3.4%;对于非理想反电动势波形无刷直流电机的研究中发现,正弦波驱动和方波驱动都会存在转矩脉动,而正弦波驱动的方式将有效减少转矩脉动。可见正弦波信号输入有一定的优越性,而本文针对正弦波信号的优越性,创新性切换研究角度,主要研究负载转矩部分,相较于方波信号,正弦波输入提高无刷电机的稳定性。

2 关键技术(方法)介绍

本实验忽略涡流,磁滞损失等问题,采用理想无刷直流电机仿真,其无刷电机内部电压平衡方程如下:

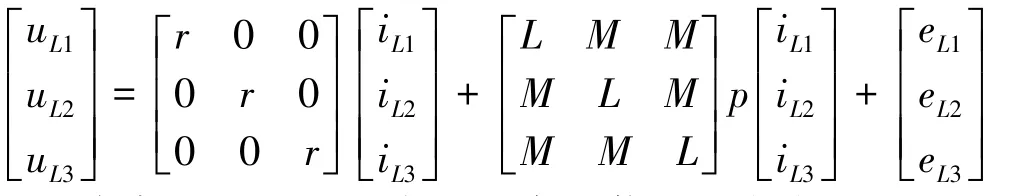
式中,uL1,uL2,uL3为电机定子绕组三相相电压;iL1,iL2,iL3为电机定子三相绕组相电流;eL1,eL2,eL3电机定子绕组三相反电势;r为电机定子绕组电阻;L为定子绕组的自感;M为定子绕组的互感;p为微分算子 。

电磁转矩方程式为:Te=(eaia+ebib+ecic)/ω

2.1 模型介绍

为了保证实验稳定性和可靠性,本实验调用了Matlab软件中自带的无刷电机模型,此模型中,参考速度为3 000 rpm,原始模型如图1所示。

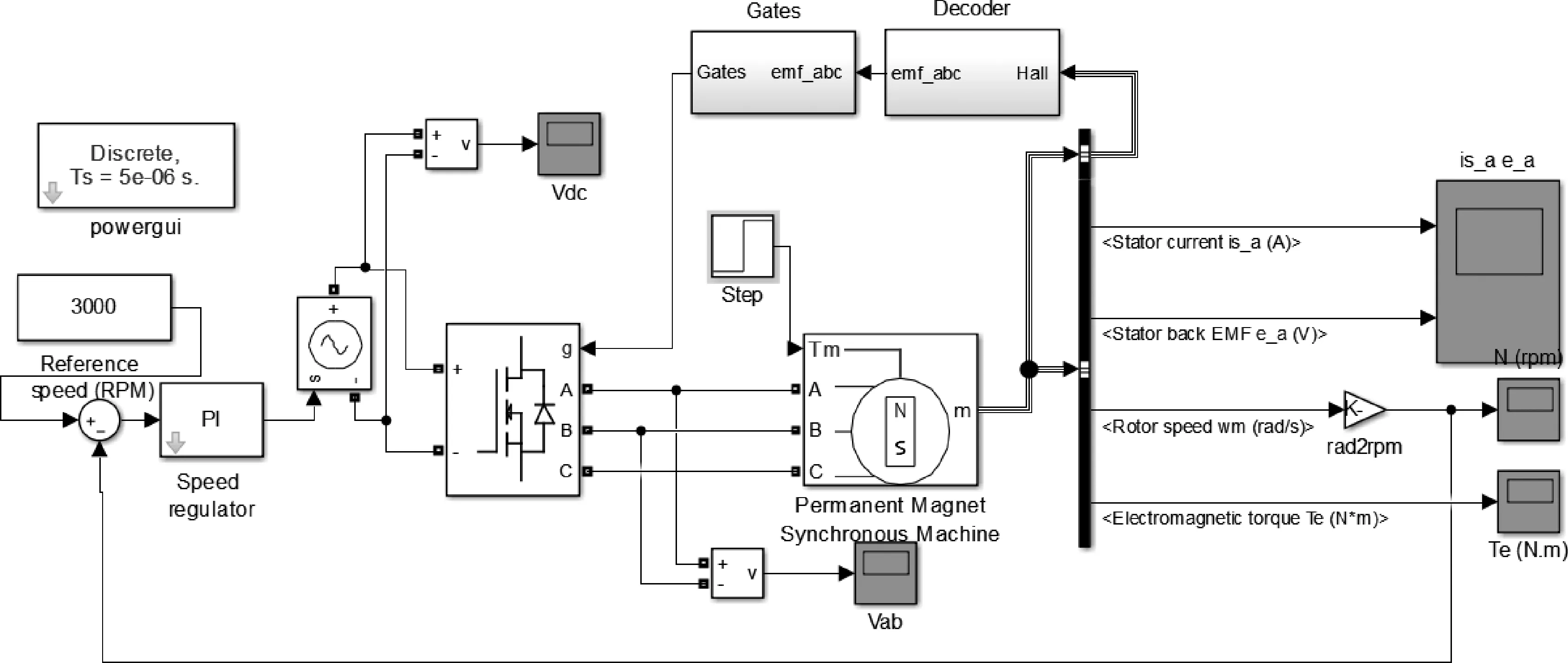
图1 原始无刷电机模型

2.2 初步实验

针对现有模型,本文进行了初步的仿真实验,仿真所用负载转矩为周期0.02 s,幅值为3 A的方波信号,其他具体实验参数见模型简介部分[2]。实验结果显示,定子电流初始波动峰值为20 A;稳定后,仍然呈现类周期性波动,波动幅值为4.5 A,波动较为激烈。电压方面,初步波动后,最终呈现类周期性波动,幅值为200 V左右,具体实验结果如图2所示。

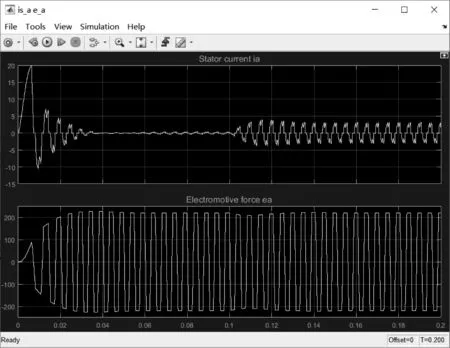
图2 定子电流和电压的初步仿真结果

2.3 优化实验模型

优化实验部分,笔者将负载转矩(Tm)变为了等幅值,同周期的正弦波信号(I=3 A,W=31.4 rad/s),同时进行相关仿真实验,取得一定效果,具体电路模型如图3所示。

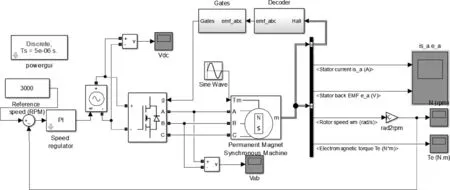
图3 优化后的具体仿真实验电路

2.4 优化实验结果

针对优化模型,本文进行了进一步的仿真实验,仿真所用负载转矩为周期0.02 s,幅值为3 A的正弦波信号[3]。可以看到,电流初始波动峰值为20 A,稳定后,仍然呈现类周期性波动,波动幅值为3 A左右,但是波动情况相较于方波信号,明显更加平稳;而电压方面,初步波动后,最终呈现类周期性波动,幅值为200 V左右,与方波信号类似具体实验结果如图4所示。

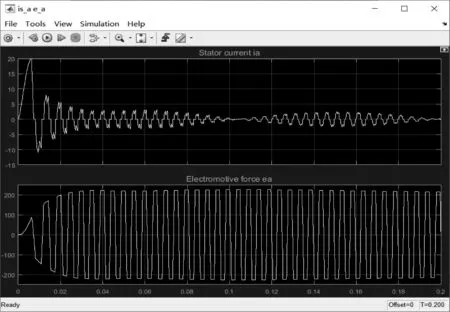
图4 定子电流和电压的优化仿真结果

2.5 优化实验小结

实验优化实验部分,主要讲负载转矩由原来的方波信号变为等幅值。同周期的正弦波信号,实验仿真结果表明,相较于方波信号的负载转矩,同条件的正弦波信号负载转矩在定子电流、转子转速、电磁转矩等方面都有显著提升稳定性的表现。本仿真实验,可以得出,同条件正弦波信号负载转矩将更有利于无刷直流电机的相关稳定性调试的结论,实验主体研究目的达成[4]。

3 结语

本文给出了一种优化无刷电机稳定性的方案,具体为将负载转矩由方波信号变为同条件正弦波信号。仿真结果显示,优化后的实验结果稳定性明显优于原有的方波信号。本实验具有一定现实意义,但由于各种限制,本实验对于此现象机理包括无刷电机反电动势的研究以及提供正弦信号负载转矩的可行性研究涉及较少,有待进一步深入[5]。综上所述,本实验提供了一种新型稳定性优化方案,对无刷直流电机的稳定性优化具有一定的研究价值和意义。