基于二相编码信号的SAR 成像

蔡永俊，牛诚翔

(中国航空工业集团公司雷华电子技术研究所，江苏 无锡 214063)

0 引言

现代战争中，雷达面临着越来越复杂的电磁环境，低截获概率(Low Probability of Intercept，LPI)雷达是一种能够提高我方战场生存能力的一种新体制雷达系统。传统SAR 雷达发射线性调频信号，但是其形式过于简单，易被截获，相位编码信号采用码型捷变技术，使得其抗干扰能力很强，但是易受多普勒频移的影响，在多普勒频移变化较大场合需要对其补偿。本文研究将二相编码信号应用于SAR 成像，并分析在SAR 信号获取过程中多普勒频移产生的影响，目标提升SAR 抗干扰和低截获能力[1-3]。

1 二相编码

二相编码信号通过调相而获得，将宽脉冲分成许多短的子脉冲，这些脉冲宽度相等，但各自以特殊的相位被发射。每个子脉冲的相位依照对应的相位编码来选择。当发射的频率不是子脉冲宽度的倒数的整数倍时，编码信号在倒相点不连续[4-6]。

对于二相码，信号的复包络为：

式中T 为子脉冲宽度，ck为第k 个码的取值(l 或-l)，码长为P。

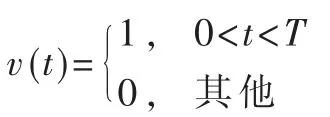
巴克码是一种二元随机序列码{cn}，cn∈{+1，-1}，n=0，1，2，…，N，其非周期自相关函数满足：

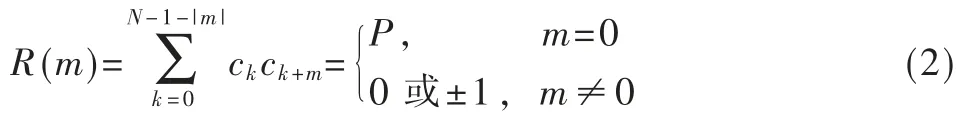
巴克码自相关函数的主旁瓣比等于压缩比，即为码长P，且有均匀的旁瓣，因此巴克码是一种较为理想的脉冲压缩信号。13 位巴克码信号形式及频谱如图1所示。

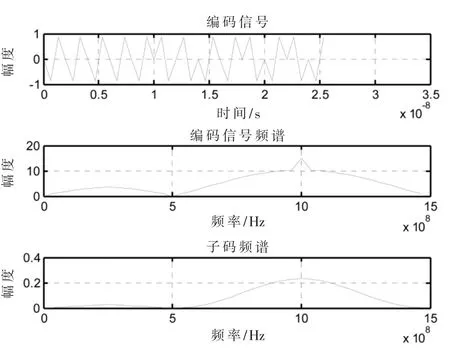
图1 13 位巴克码信号形式及频谱

m 序列通常采用线性逻辑反馈移位寄存器来产生，一般来说，一个n 级线性反馈移位寄存器可能产生的最长周期等于2n-1，最长线性反馈移位寄存器序列的简称也就是m 序列。由于m 序列具有周期性，其自相关函数也具有周期性。它的周期自相关函数很理想，但是，它的非周期自相关函数就不尽如人意，如果序列长度为N，当N＞＞1 时，主旁瓣比接近于。不同码长m 序列及127 位m 序列频谱如图2 所示。

由上述结果可知，二相编码信号的脉压特性主要由码长决定，而信号的频谱主要取决于子脉冲的频谱。

与LFM 信号相比，相位编码最突出的一个问题便是“多普勒敏感性”[7]，即当回波信号存在一定的脉内多普勒频移时，对于回波信号是一种内调制，破坏了匹配滤波器的相关性。随着多普勒频移的增加,相位编码信号脉冲压缩的处理结构与脉内多普勒偏移失配，会导致脉冲压缩后信号主瓣展宽，峰值下降，旁瓣升高，影响了距离分辨率，严重时信号无法检测[8-9]。下文将基于非“停走停”假设推导回波准确的表达式，从本质上阐述脉内多普勒偏移的由来，并以此分析多普勒敏感性对于SAR成像的影响。

2 非“停走停”假设下回波信号表达式

SAR 成像几何中，不考虑“停走停”假设，雷达与目标的瞬时斜距为：

在距离时间t=0 处进行泰勒级数展开，由于在极短的脉冲持续时间内，因此可忽略其二次及更高次项的影响，展开后瞬时斜距可表示为：

所以，当t=0 时，R(ta，0)=Ra。雷达的发射波形抵达目标的时间为：

设在极短的脉冲调制周期内雷达与目标的径向速度保持不变，则雷达照射到目标时的瞬时斜距为：

则目标的回波延迟为：

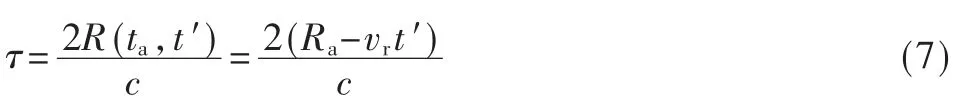
结合以上几式可得，目标回波延迟为：

代入回波信号表达式：

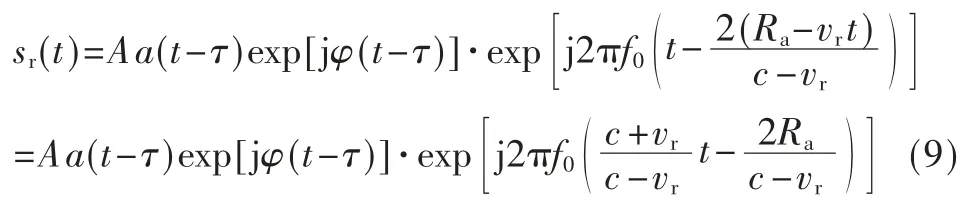
由于vr=c，则：

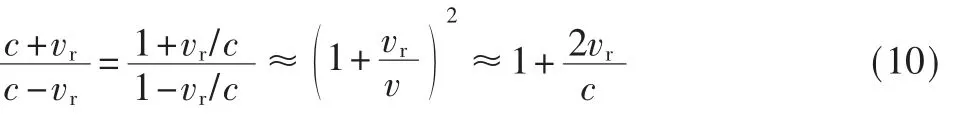
所以回波信号表达式为：

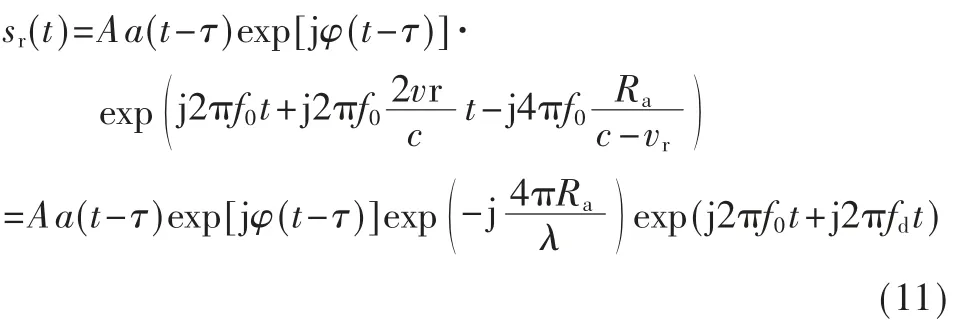
下变频后的回波信号表达式如下：

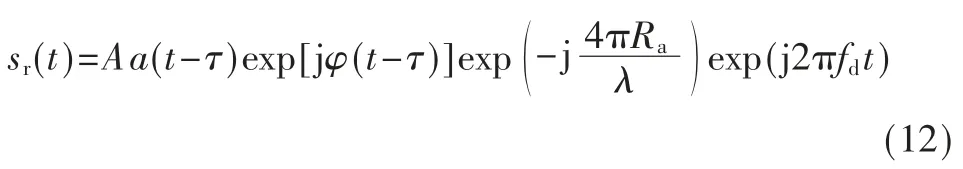
其中，A 是目标对发射信号的幅度调制，为信号窗函数，第一个指数项为相位编码信号序列，第二个指数项为方位相位表示雷达与目标相对运动的多普勒历程，由第三个指数项可知，回波信号存在着附加的多普勒偏移。由于上式回波信号是在不考虑“停走停”假设情形下推导出的，因此对于相位编码信号而言，该频率属性为脉内多普勒频率，是在单个脉冲从发射到接收其回波这一“快时间”内产生的多普勒频率。而与之不同的是，第二个指数项包含的是对于方位成像有益的脉间多普勒频率，是两个发射脉冲在其“慢时间”间隔产生的多普勒频率[10-12]。

3 距离多普勒成像

由上文分析可知，相位编码信号的峰值旁瓣比只取决于编码长度P，理论上可以通过增加编码信号长度来提升峰值旁瓣比，但由上节可知，一味地增加码长将导致回波信号对多普勒频移更为敏感，对于多普勒频移较大的应用场合，将导致峰值旁瓣比迅速下降甚至失配从而抵消通过增加码长来提升峰值旁瓣比的效果，因此多普勒频移对回波脉压的实际影响需要结合具体应用场景及实际系统参数而具体分析，当发射脉宽确定，若码长太小将导致回波自相关性能下降峰值旁瓣比降低，若增加码长也将同时导致码元宽度的减小，从而也会增加系统的复杂性[13-15]。

相位编码信号具有复杂的相位结构是低截获概率雷达信号的主要形式之一[7]，下文结合实际场景利用Baker 二相码进行SAR 成像仿真，并分析脉内多普勒偏移在SAR 成像模式下的影响。

距离多普勒(RD)成像算法其基本思想是将二维的匹配滤波的过程分解成两个一维处理的级联[8]，先对回波信号进行距离向匹配滤波，然后将信号变换到距离多普勒域，通过插值来校正由于相对运动所引起的距离徙动，最后通过方位向匹配滤波实现数据的完整聚焦处理。其中距离向利用脉冲压缩实现高分辨，方位向利用脉间多普勒信息实现方位聚焦。

(1)脉内多普勒频移补偿

由于SAR 成像主要针对地面静止目标，因此对于脉内多普勒频移的补偿与对空搜索等主要针对动目标的场合不同，只需要补偿地速引起的脉内多普勒频移即可，补偿因子为：

补偿后信号表达式为：

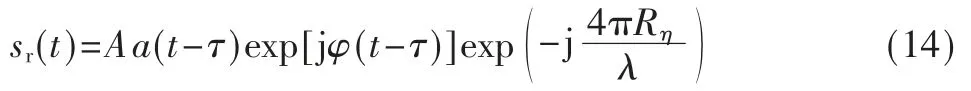
(2)距离压缩

距离压缩依靠相位编码信号的回波和相位编码的本振信号进行求自相关。对SAR 回波距离压缩，第一步对回波进行快时间域傅里叶变换，可得：

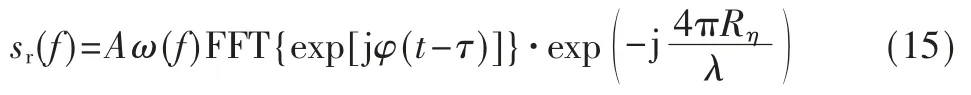
同样对相位编码本振信号复共轭进行傅里叶变换：

将sr(f)与sm(f)相乘然后进行IFFT 得到：

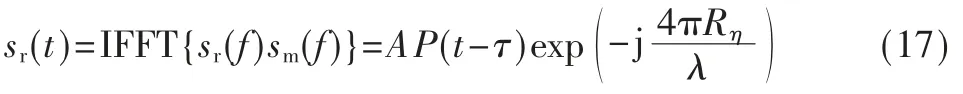
其中P(t)为宽度为2T 的一个编码信号压缩脉冲。

(3)距离徙动校正

对于小斜视角情形，点目标瞬时斜距可以表示为：

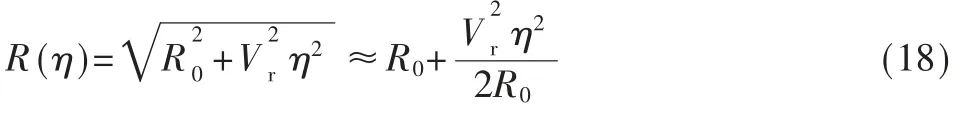
将上式代入式(17)：

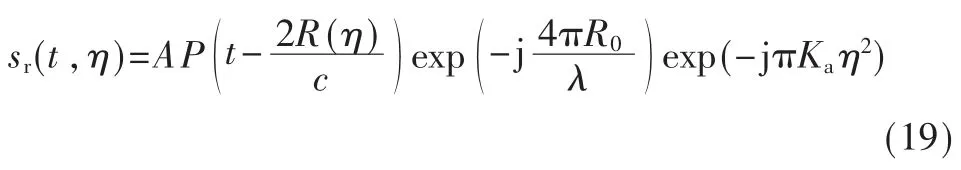
由于距离相同方位位置不同的所有目标的距离徙动(RCM)轨迹在距离多普勒域轨迹重合，因此在距离多普勒域对一个目标的RCM 校正等同于对一组目标的RCM 校正，此时RCM 表达式为：

将式(19)进行方位向傅里叶变换可得到信号在距离多普勒域的形式：

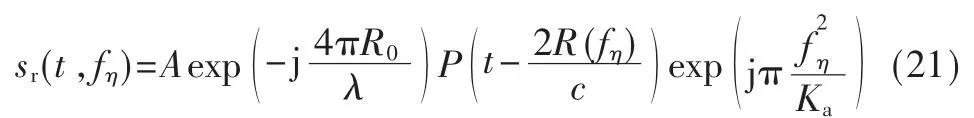
经过距离徙动校正后，信号在RD 域的表达式为，

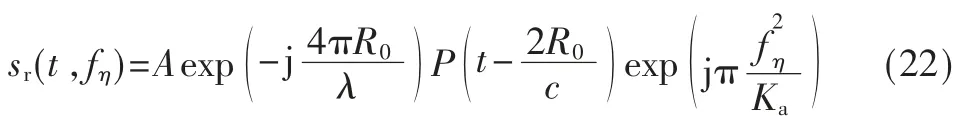
此时，所有目标回波轨迹在距离多普勒域均为一条直线，可以进行方位向匹配滤波完成场景的聚焦。

(4)方位压缩

方位向匹配滤波的参考函数为：

将式(22)与式(23)相乘并进行傅里叶逆变换即可完成方位压缩：

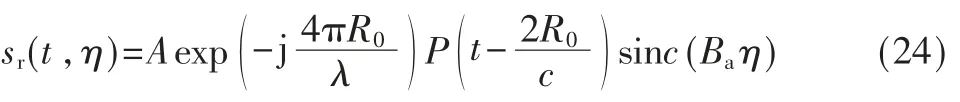
其中Ba为方位多普勒带宽。

算法流程图如图3 所示。

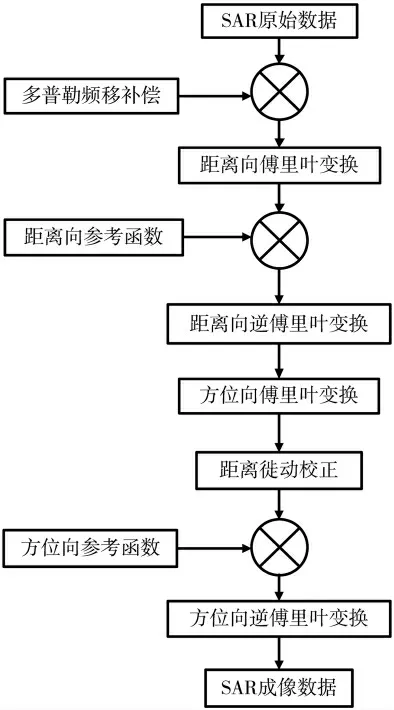
图3 距离多普勒成像流程

4 仿真分析

根据上文对相位编码回波信号及波形参数分析，选用127 位m 序列作为发射信号为例仿真距离多普勒成像。仿真参数如表1 所示。

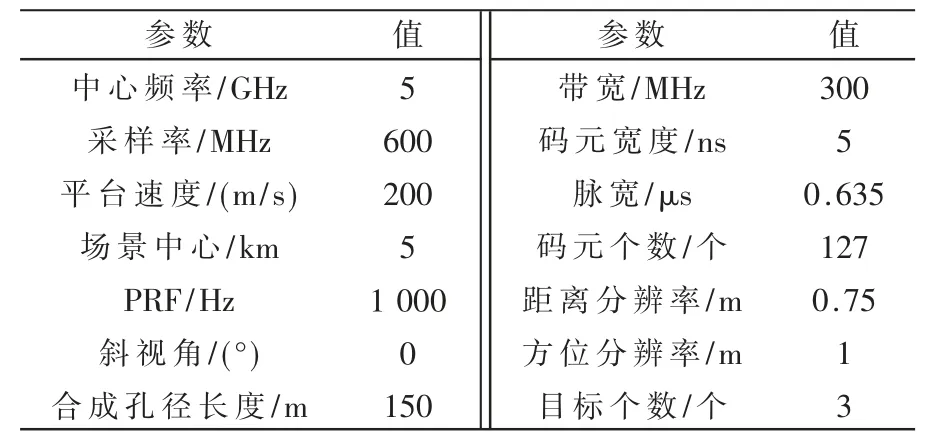
表1 仿真参数

经过距离徙动校正后，回波数据域方位向上最大值在一条线上，校正前后如图4 所示。

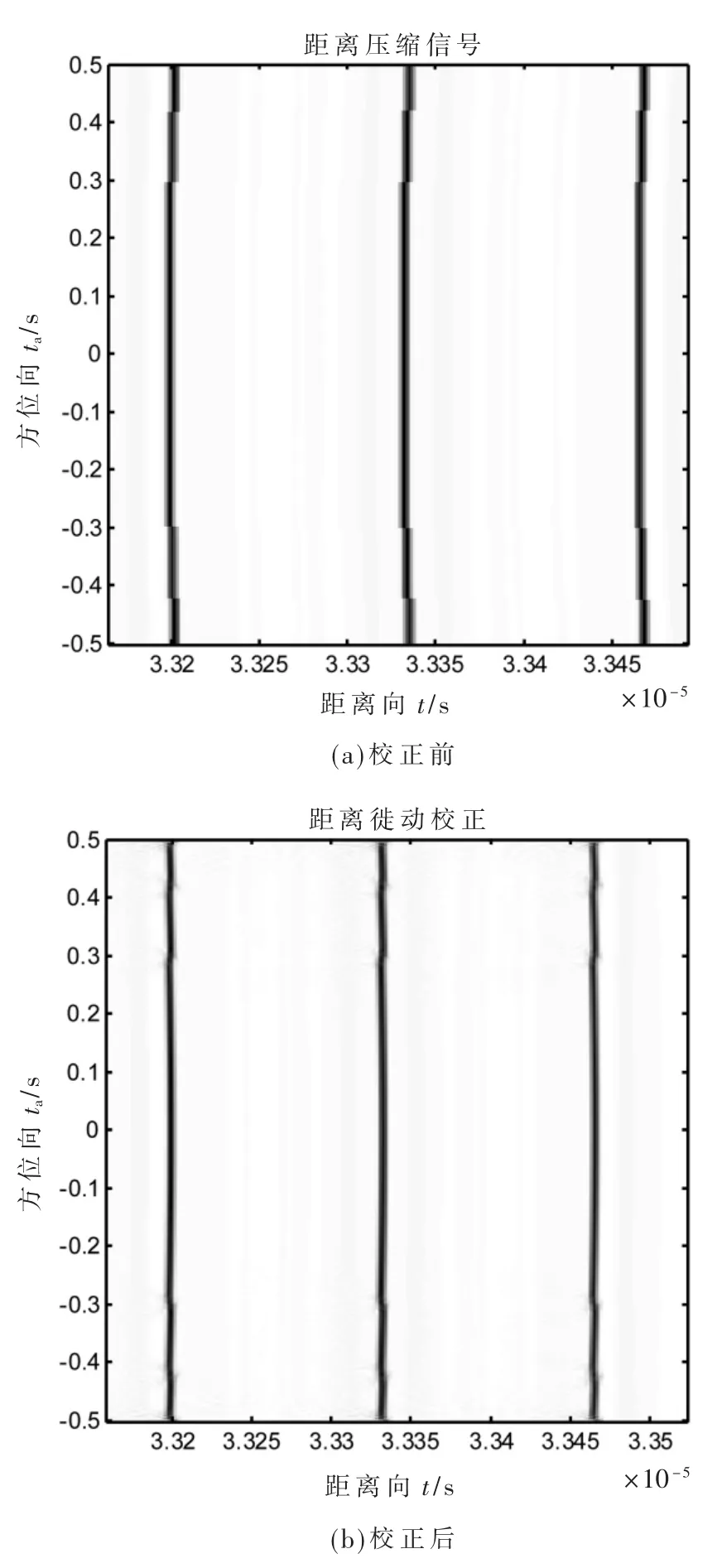
图4 距离徙动校正前距离徙动校正

编码信号由于存在脉内多普勒敏感现象，在该系统参数下分析多普勒频移对成像结果的影响，结果如图5所示。发现当有多普勒偏移时即不补偿多普勒频移时，成像结果剖面与补偿多普勒频移时几乎重合，表明在该系统下多普勒偏移对成像结果几乎没有影响。

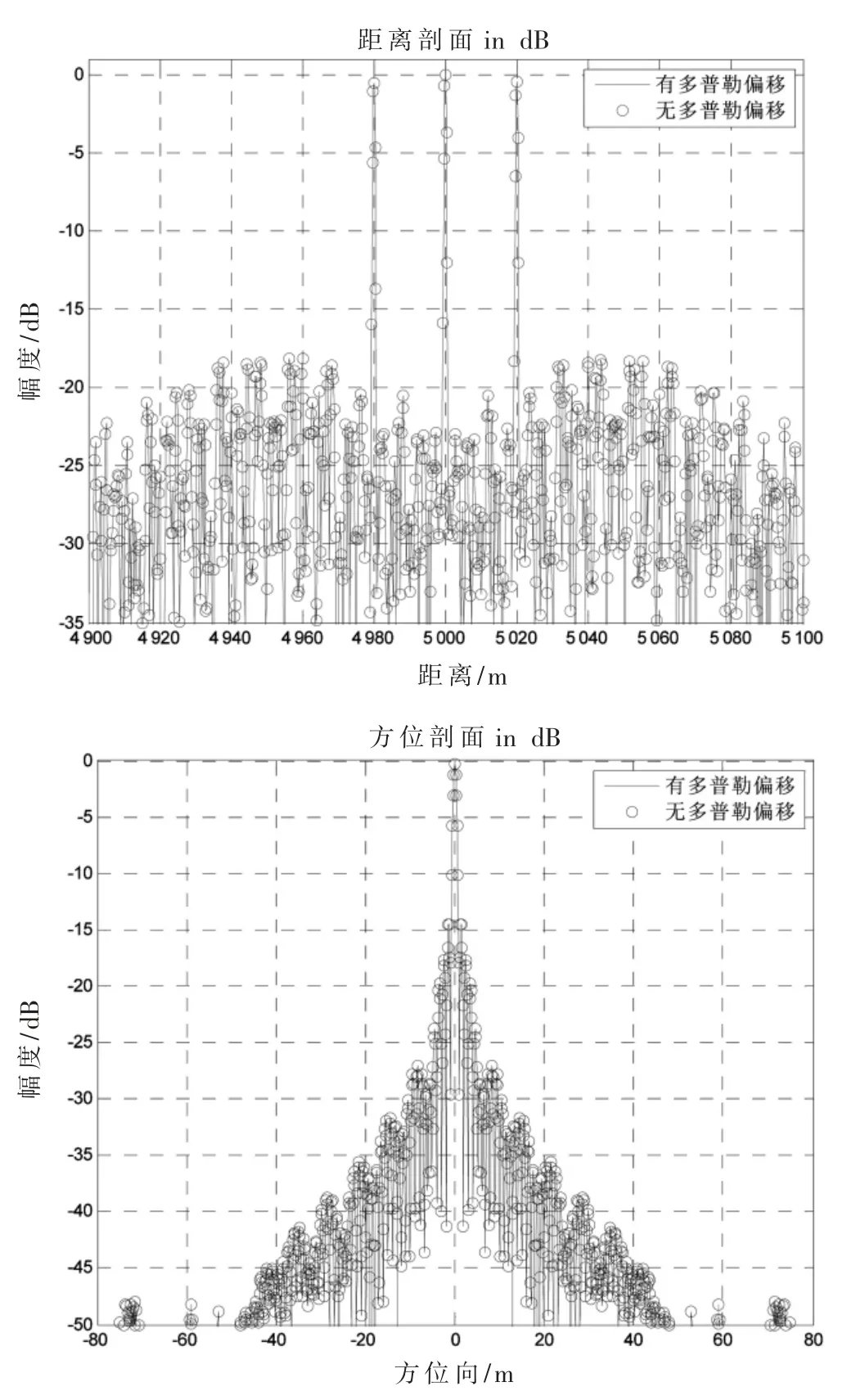
图5 距离剖面方位剖面

多普勒偏移引起的主瓣增益损失如图6 所示，点图像及等高线图如图7 所示。通过仿真参数知，该系统下的最大脉内多普勒偏移值为75 Hz，而图6 显示了当存在多普勒偏移值时成像处理目标增益的损失随脉内多普勒频率的变化关系曲线。由图可知，当多普勒偏移引起主瓣增益损失达到3 dB 时需要的偏移值为696.5 kHz，而在该组仿真参数的SAR 模式中最大的多普勒偏移值为75 Hz，远远小于696.5 kHz，所以此时多普勒偏移对成像结果的影响可以忽略不计，成像剖面图符合预期。因此该波形参数及雷达参数下，多普勒变化较窄，多普勒容限较宽。

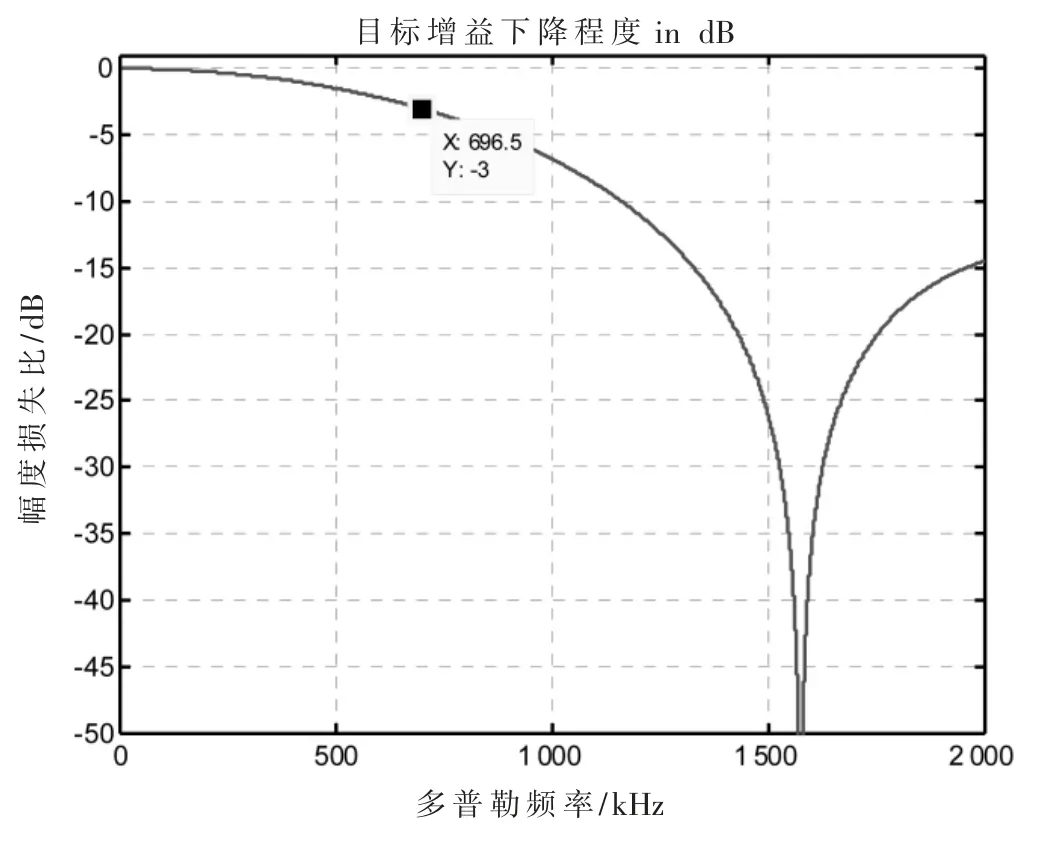
图6 仿真参数下多普勒偏移引起的主瓣增益损失

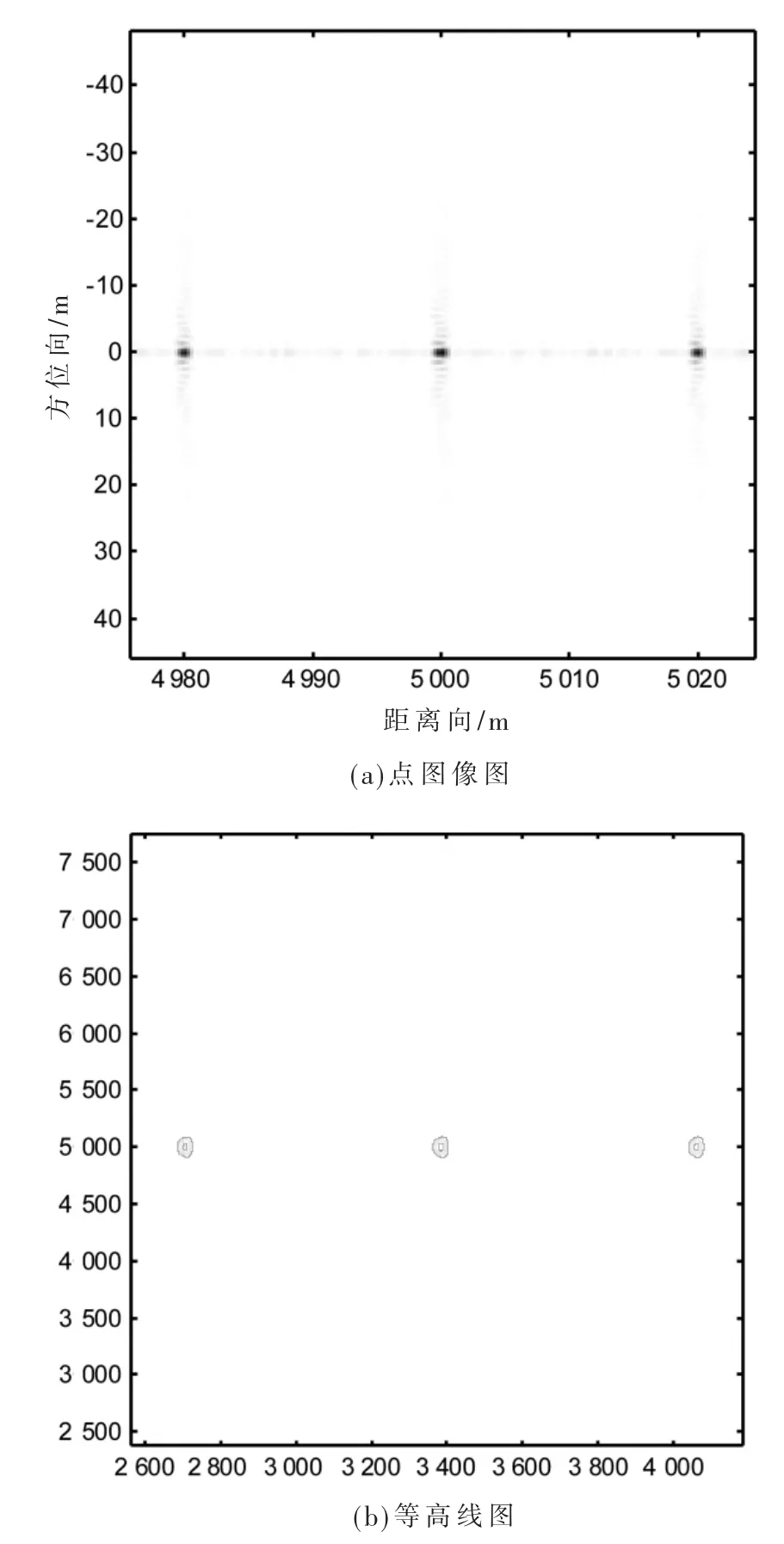
图7 点图像及等高线图

同时，由剖面图可知，距离旁瓣电平为-18.15 dB，方位旁瓣电平为-14.5 dB。

5 结论

本文从非“停走停”假设角度推导了回波信号的准确表达式，从本质上去揭示了相位编码信号的脉内多普勒偏移的来源，并基于此分析相位编码信号的多普勒敏感性。对于SAR 成像处理，由于成像一般针对地面静止目标，其频率偏移受载机速度和姿态的影响，可以事先由雷达参数得出，只需在距离向处理时在不同方位时刻分别补偿掉脉内多普勒偏移，当偏移远远小于多普勒容限时可以忽略。最后通过仿真验证了本文分析的有效性。