基于全连接神经网络的车辆短预瞄电磁导引方案*
杨豫龙 ,赵 娟 ,2,黄 原
(1.中国地质大学(武汉) 自动化学院,湖北 武汉 430074;2.复杂系统先进控制与智能自动化湖北省重点实验室,湖北 武汉 430074)
0 引言
通有交变电流的导线附近会产生磁场。电磁导引利用这一特性,通过预先铺设在路面的电磁线,实现对车辆的导引[1]。相较于视觉、雷达、卫星定位等引导方式[2],电磁导引方案对环境的抗干扰能力较强,不易受外界光照、天气等条件的影响[3],广泛应用于工业、物流等路径相对固定的场景中[4]。
为实现车辆电磁导引,文献[5]通过一行紧密排布的传感器,检测车身相对路面电磁线的位置。文献[6]利用最小二乘法,对当前位置处的电磁感应强度与车身侧向偏移量的函数关系进行曲线拟合,从而确定车身相对路面的位置。文献[7]提出一种“差比和”算法,用两传感器值之差除以两传感器值之和来描述车身的侧向偏移量,然后使用PID 控制器实现跟随。
但上述方案仍未解决阻碍电磁导引发展的根本问题,即:电磁传感器的探测距离十分有限,导引速度难以提高,若使用延长杆等机械结构增大电磁传感器探测距离,会导致车辆体积庞大、机械性能变差。
因此,本文利用神经网络模型优异的特征学习能力,提出一种基于全连接神经网络模型的车辆短预瞄电磁导引方案。实验结果表明,该方案极大优化了电磁导引在短预瞄车辆上的控制效果,同时,使电磁导引系统变得小型化和轻量化,拓展了其在小型车辆无人驾驶领域的应用前景。
1 车辆预瞄跟随模型
根据郭孔辉的预瞄跟随理论[8-10],建立四轮自动导引车辆的单点预瞄跟随模型。记R 为车辆转弯半径,L为轴距,i 为转向系传动比,δ 为舵机转向角,车辆的运动服从Ackermann 几何关系:

讨论车辆在既定路线上行驶的情况,路线中心位置表示为f(t),车速记为v。在t 时刻,车辆具有瞬时状态y:

设传感器前向预瞄距离为d,则预瞄时间T 为:

经时间T 后,车辆的横向位置记为:
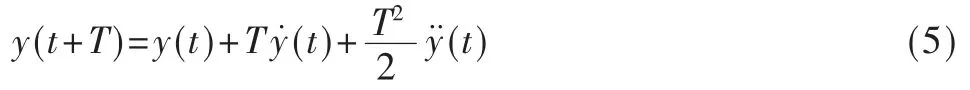
在上述假设条件下,希望车辆能够实现对预瞄点的跟随,即沿曲率为的轨迹行驶距离d 后,在(t+T)时刻到达的预期位置f(t+T)。该过程表示为:
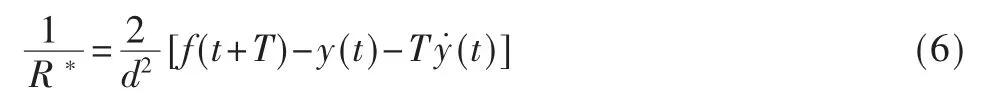
由此得到,要使车辆运动到所期望的预瞄位置,即y(t+T)=f(t+T),控制系统输出舵机转向角加速度应该为:
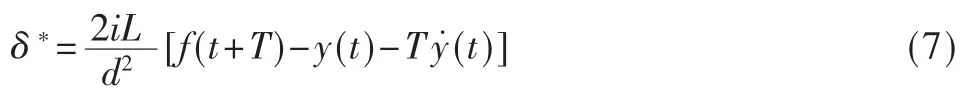
综上所述,画出如图1 所示的控制系统方框图。由于车辆的转向机构动作存在一定的时滞,在高速行驶状态下,该时滞不能被忽略不计,因此,引入一阶滞后环节e-τs。系统的传递函数为:

图1 车辆预瞄跟随控制系统方框图

在这个存在滞后环节的车辆转向控制系统中,要提高运行速度,必须增大预瞄距离。因此,对高速运行车辆前方的道路进行超前探测是一种克服控制系统自身时滞,获得更好控制效果的可行方案。若只提高车辆运行速度而不增大预瞄距离,则会导致车辆的侧向控制跟随效果变差,甚至发散[11]。
2 传感器布局设计
传感器的布局直接影响到电磁导引的方案设计,因此,首先通过分析确定传感器的最佳布局方式。
实验环境采用20 kHz 正弦波产生变化的磁场作为电磁导引信号。传感器为10 mH 电感与6.8 nF 电容构成的LC 谐振电路,谐振频率与磁场频率匹配。
当车身上的电磁传感器高度固定时,电磁感应强度与传感器侧向偏移距离呈负二次幂关系。从图2 可以看出,使用单个电磁传感器只能确定车身侧向偏移距离的绝对值,而不能确定偏移的方向。
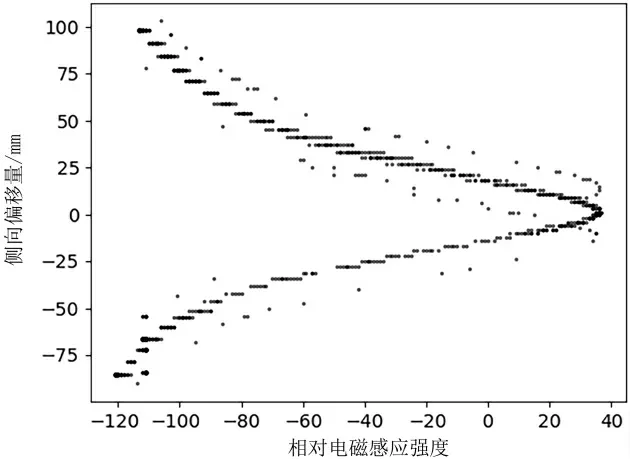
图2 单个传感器电磁感应强度与侧向偏移距离关系
为获取更多车身姿态信息,本文将传感器的数量增加至7 个,并按图3 所示相对位置排布。此时,分析多个传感器之间的相互关系。

图3 电磁传感器排布位置示意图
将同一行上两个相互对称的电磁传感器作为一组,例如图3 中的S1 和S5,绘出电磁感应强度与侧向偏移距离的关系,如图4 所示。根据两个传感器的值,能够唯一确定一个偏移量。这说明两个对称排布的传感器能够确定电磁导引车辆的侧向偏移方向和偏移距离,即完全确定车身在水平方向上的位置。
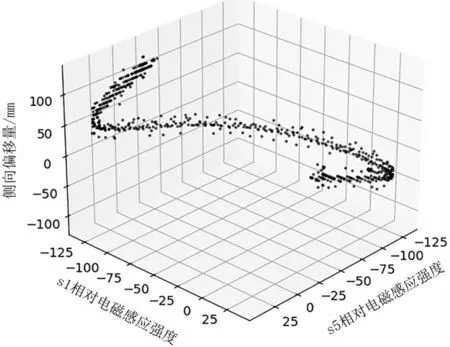
图4 对称位置传感器电磁感应强度与侧向偏移距离关系
将同一对角线上的两个电磁传感器作为一组,例如图3 中的S1 和S7、S5 和S6。将两个传感器测得的电磁感应强度作差,绘出该差值与车辆行驶方向相对电磁线偏离角度(以下简称纵向偏移角度)的关系,如图5 所示。由图可见,曲线在-30°~30°范围内具有较好的线性特性。这说明呈对角线排布的一对传感器能够反映车身纵向偏移角度的变化。
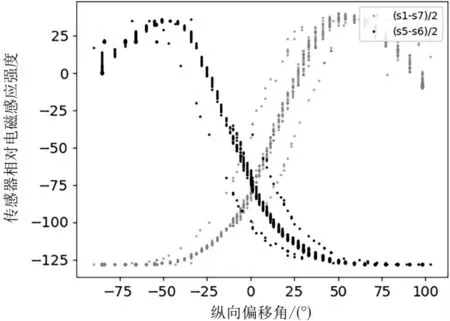
图5 对角位置传感器电磁感应强度差值与偏移角度关系
本文根据此传感器排布方案,搭建一辆四轮车模型,如图6 所示。其中,7 个电磁传感器按图3 排布方式分别安装在车身的前部和中后部。车模长为295 mm,宽为199 mm,高为95 mm,轮距为153 mm,轴距为202 mm。传感器最前端到前转向轮轴心沿前进方向的水平距离为42 mm。考虑到电磁传感器的探测距离极短,可认为该车模电磁导引系统的预瞄距离为42 mm,约为车身轴距的1/5。

图6 本文所使用的四轮车模
除此之外,车模上还搭载了一套独立的摄像头导引系统,其预瞄距离达300 mm。该系统仅用于在神经网络训练阶段,引导车模在实验环境中以3.2 m/s 的速度稳定运行,以获得高质量的数据集。
3 全连接神经网络模型
在人工神经网络模型中,神经元是一种多输入、单输出的非线性模型[12]。基于神经元模型,搭建一种5 层全连接神经网络,如图7 所示。输入层包含7 个神经元,分别用于接收S1~S5 5 个电磁传感器数据,以及(S1-S7)/2、(S5-S6)/2 两对传感器的差比和数据;神经网络设置3层隐含层;输出层神经元个数为1,输出结果作为控制量输出至舵机。
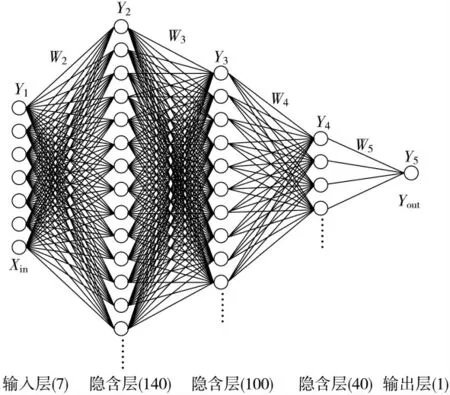
图7 全连接神经网络模型
基于多次实验结果,综合权衡使用不同激活函数的利弊[13],本文选择tanh 函数作为隐含层第一、第二层的激活函数,选择ReLU 函数作为隐含层第三层的激活函数。

将神经网络输入矩阵记为Xin,输出矩阵记为Yout,各层输出矩阵记为Yn,权值矩阵记为Wn,偏置矩阵记为Bn,其中整数n∈[1,5]。该全连接神经网络模型的完整结构表示为:

不失一般性地,忽略隐含层之间的复杂关系,将上述神经网络模型看作输入Xin到输出Yout的映射h(Xin;θ),其中θ 为神经网络模型参数矩阵,包括权重W 和偏置B,基于该映射构造均方差(Mean Square Error,MSE)损失函数L(Yi,Xin)作为目标函数:
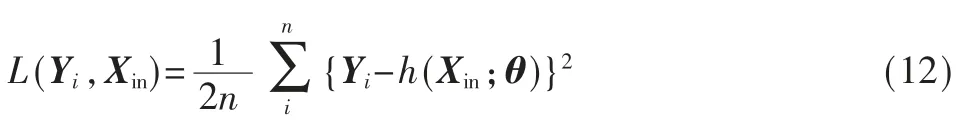
全连接神经网络训练的基本方法是首先通过正向计算误差,然后将该误差反向传播。每一层参数的更新依赖于后一层的损失,各层利用梯度下降法更新参数,如式(13)所示。

式中,梯度即目标函数L(Yi,Xin)对参数θ 的偏导数,α为学习率。
由于使用的训练集数据量较大,为了提高迭代速度,将训练集划分为m 个大小为n 的样本,进行小批量梯度下降[14]。由式(12)、式(13),得到式(14):
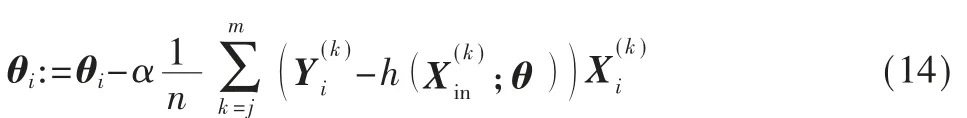
神经网络的训练过程就是通过上述方法不断迭代训练,寻找参数θ 的最优解,使目标函数趋于全局最小的过程。训练流程如图8 所示。

图8 神经网络训练流程图
在训练开始前,向神经网络模型提供一套合适的初始参数[15],然后,使用Adam 优化器在每次迭代时指引神经网络各个参数向正确的方向更新。在每次模型迭代后,使用测试集验证新模型的性能,以决定是否保留该模型,并根据验证结果调整学习率继续迭代,直至MSE值下降到所期望的范围以内,或训练再无进展。
4 系统性能测试
本次训练使用的数据集总量为75 464 条,每20 次训练为一次迭代,共迭代200 次。训练过程的MSE 下降曲线如图9 所示。从图中可以看出,训练前期MSE 下降迅速,随后下降趋于平缓,最终训练集和测试集MSE 均稳定在0.002 左右,低于预期目标MSE 值0.005,说明该神经网络模型训练结果较好。

图9 神经网络模型训练MSE 下降曲线
在将神经网络模型部署到车模之前,对模型进行模拟运行测试。为了避免模型对单一数据集可能存在过拟合现象,模拟测试是在不同的场地上重新采集数据,然后将传感器数据按时间顺序依次输入训练好的模型进行预测,以模拟车辆在场地上的运行过程。由于摄像头导引系统具有很好的控制效果,可以将其输出结果视为标准结果。然后将神经网络模型的实时输出结果与标准结果进行对比,如图10 所示。结果表明,神经网络模型输出结果与摄像头导引方案的实际控制量基本一致,证明该模型跟随情况良好,已经具备较强的控制能力。
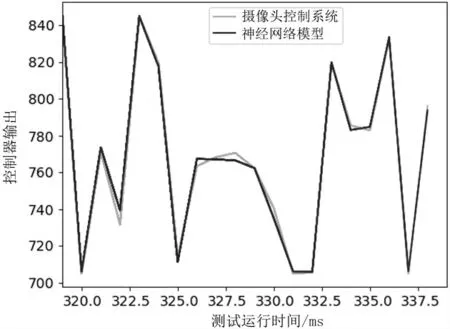
图10 神经网络模型运行模拟测试
完成模拟测试后,将神经网络模型部署至车模。在同一场地上,使用同一短预瞄车模,分别使用传统“差比和”PID 算法[7]和本文构建的全连接神经网络模型控制车模运行,记录车模在不同运行速度下偏离路线中心线的最大距离,如表1 所示。从此表可以看出,当车模低速(1 m/s)运行时,两种方案均具有较好的控制效果;随着运行速度的提高,前者受预瞄距离的限制,控制效果迅速变差,出现较大幅度的震荡,而后者依然能保持较好的控制效果;当速度提高到2.5 m/s 时,前者已经无法引导车模按照正确路线运行,后者的控制精度有所降低,但依然能够引导车模正常运行。因此,全连接神经网络模型不论是最高运行速度,还是控制稳定性与精度,较传统电磁导引算法均有较大提高,极大地改善了短预瞄电磁导引的控制效果。
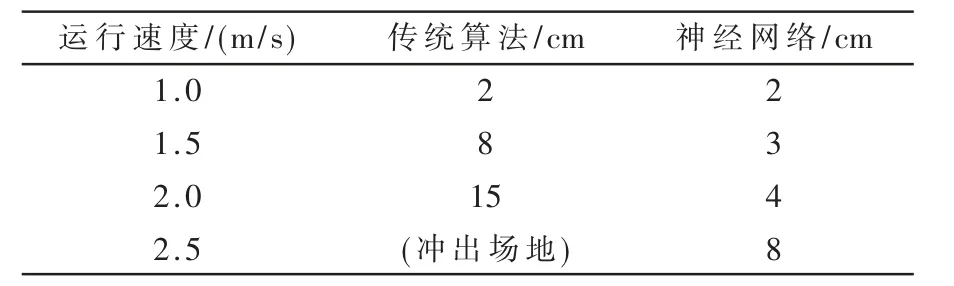
表1 不同导引方案运行过程中的最大侧向偏移距离
5 结论
本文提出了基于全连接神经网络模型的车辆短预瞄电磁导引控制方案。该方案利用全连接神经网络出色的非线性拟合能力,从短预瞄电磁传感器的有限数据中挖掘出尽可能丰富的车身位置、姿态等信息,基于这些信息对前方道路进行预测,从而弥补预瞄距离不足的缺陷,达到更好的控制效果。测试结果表明,其控制精度和最大稳定运行速度均远远超出传统的电磁导引控制算法。同时,本方案大大缩小了电磁导引系统的体积,拓展了电磁导引在小型车辆上的应用场景。电磁导引依靠其价格低廉、抗干扰能力强的优势,有望为未来无人驾驶技术提供新的思路与方式。

