互补谐振耦合型电磁式直线位移传感器

赵 静，汤其富，彭 松，李 咪，郭羊庭

(重庆理工大学，机械检测技术与装备教育部工程研究中心，重庆 400054)

0 引言

直线位移的测量在工业领域中极其重要，直线位移传感器为获得精密的直线位移提供了便利和保障。工业生产制造中常用的直线位移传感器可以分为电场式、光电式和磁场式3种类型[1-3]。电场式直线位移传感器包括容栅和电场式时栅等，它们能达到较高的测量精度但环境适应性较差；光电式直线位移传感器包括激光干涉仪、光栅和光场式时栅等，它们的测量精度极高但生产要求和使用要求都较高；磁场式直线位移传感器包括感应同步器、Balluff BIP系列传感器、LVDT、磁栅、磁场式时栅和Zettlex传感器等，虽然它们的测量精度不及前两种，但由于具有较大的量程且是基于电磁感应原理的传感器，所以能应用于有油污、粉尘、冲击振动等环境恶劣的工业领域[4-5]。另外，采用PCB(printed circuit board)技术的平面型电磁感应式直线位移传感器使得该类型的传感器更易于设计制作[6-7]。作者在研究电磁感应式直线位移传感器时发现，文献[8]研究的传感器原始误差小于15 μm，但由于其在动尺和定尺上均引线，且动尺和定尺最大间隙不大于0.5 mm，因而使用场合受限；文献[9]研究的传感器的动尺采用导磁体，降低了使用要求,但原始误差较大，达到了100 μm以上；文献[10]研究的传感器采用无源谐振电路作动尺，但由于定尺结构和单边传感等问题，原始误差在80 μm左右。针对上述问题，本文开展了互补谐振耦合型电磁式直线位移传感器的研究，在传感器的安装及使用要求方面和原始测量精度方面进行提升。

1 传感器的结构和工作原理

1.1 传感器结构

传感器由1块定尺和2块动尺组成，其基本结构如图1所示。传感器定尺采用的结构是基于文献[5]和文献[11]而提出的改进型结构。动尺安装在动尺基体上随运动部件做直线运动，定尺安装在定尺基体(图中未画出)上保持静止。每个感应线圈中的导线正反绕制后首尾串联，可以使得在没有动尺时，各感应线圈中的感应电动势为0，从而使感应信号尽可能地只与动尺位移相关[12]。

图1(c)所示的定尺上有2个按正弦形状布置的感应线圈，感应线圈Ci1和Ci2的结构周期长度都为L，Ci1和Ci2在测量方向(X)上相差L/4。激励线圈Ce按矩形形状布置在感应线圈四周。动尺有2块，每块上有1个线圈Cm，Cm在测量方向上的宽度为L/2。

1.2 传感器工作原理

该传感器工作时，在激励线圈中通以交流信号，则激励线圈周围产生交变磁场，该交变磁场以共模方式对感应线圈产生作用。由于感应线圈采用对称的正反向绕制结构，所以激励磁场在感应线圈中被抵消，理论上不引起感应电动势。2块动尺上的线圈接收激励磁场，感应出的交变电流使其产生自身的交变磁场，该交变磁场以差模方式作用于感应线圈。随着动尺的移动，动尺上的磁场周期性地改变感应线圈中的磁通量，在感应线圈中产生与动尺位移有关的感应电动势(感应信号)，从而基于该感应信号得到直线位移信息[13]。

设激励线圈中通入的交流激励为

U(t)=Umsin(ωt)

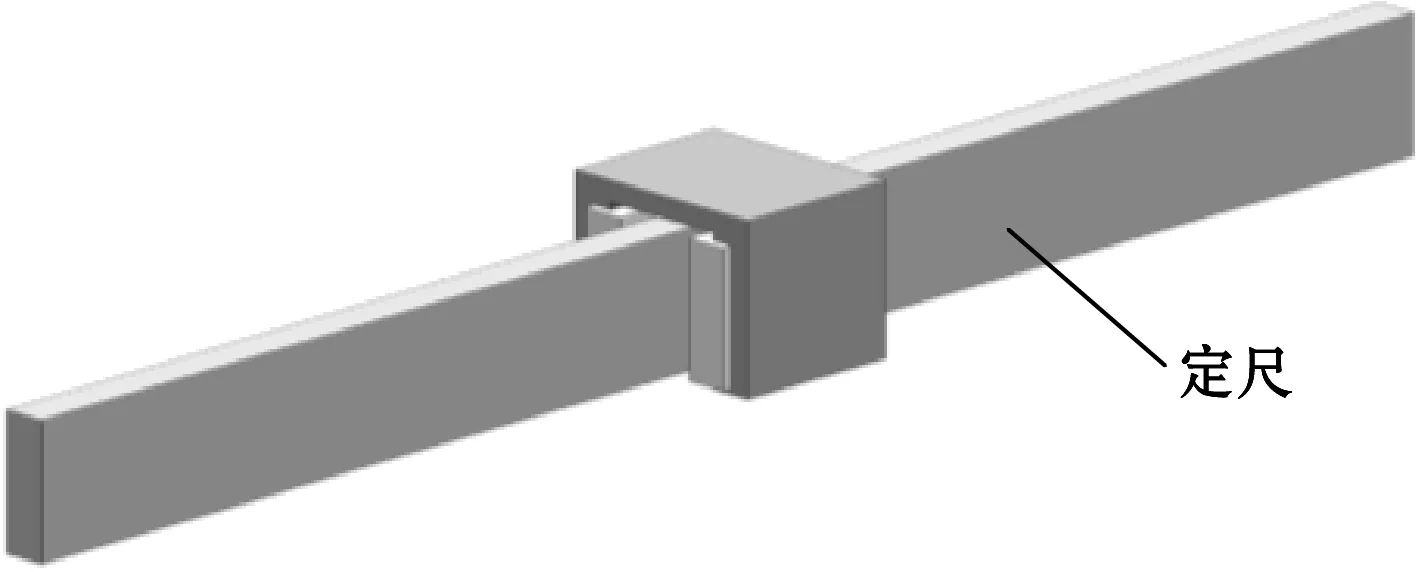
(a)传感器总体结构图

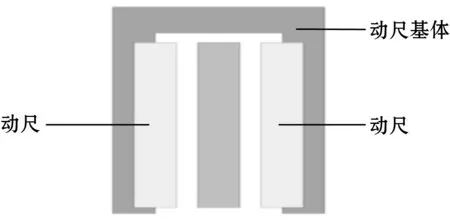
(b)传感器总体结构左视图

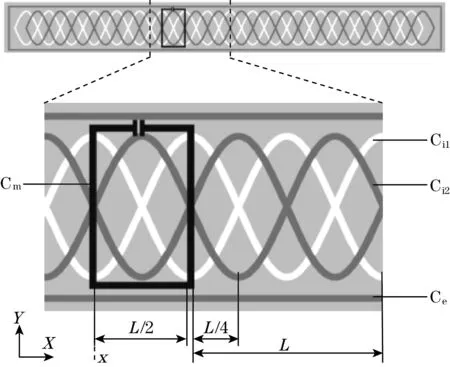
(c)动定尺结构示意图图1 互补谐振耦合型直线位移传感器结构示意图

则在矩形激励线圈周围产生近似均匀的交变磁场，其磁感应强度为

B=aUmsin(ωt)

式中a为常量系数。

由于矩形激励线圈周围产生的磁场近似均匀分布，所以动尺线圈中的磁通量可近似表示为

Φ=BS=aSUmsin(ωt)

式中S为动尺线圈垂直于磁场方向的面积。

从而根据法拉第电磁感应定律，在动尺线圈上产生的感应电动势为

(1)

则由动尺线圈产生的磁感应强度为

B=-abωSUmcos(ωt)/R

式中：b为常量系数；R为动尺线圈的交流阻抗。

设感应线圈1和感应线圈2的函数分别为

f1(x)=Asin(2πx/L)

f2(x)=Acos(2πx/L)

式中：A为幅值；L为感应线圈1和感应线圈2的重复结构周期长度；x为动尺线圈最左侧的增量位移，如图1(c)所示。

动尺线圈在测量方向上的宽度为L/2。如果规定感应线圈中感应电流向X正向一侧流动时感应线圈中的磁通量为正，则感应线圈1中的磁通量为

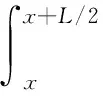
(2)

同理，感应线圈2中的磁通量为

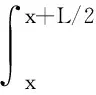
(3)

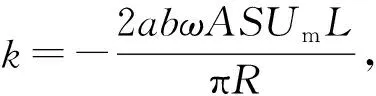
(4)

(5)

由于2块动尺均参与传感，所以最后感应线圈1、2中的感应电动势分别为

(6)

(7)

显然，以上2路信号是以传感器动尺直线位移为调制信号、与激励信号同频率的信号为载波的调幅波。随着动尺的移动，这2路感应信号幅值变化而相位不变，于是可以用鉴幅信号处理方式进行后续的处理。可以得到：

(8)

求反正切得动尺线圈相对于感应线圈1和感应线圈2走过的增量位移：

(9)

该传感器采用基于鉴幅的信号处理方法，其信号处理模块的工作原理如图2所示[14]。由FPGA产生频率为2 MHz的方波，作为激励信号。感应信号经过开关混频、低通滤波和放大后，代表动尺直线位移的低频成分被放大。然后，信号经过模数转换器成为FPGA可以直接处理的数字量，FPGA对这些数字量进行反正切运算得到动尺位移。

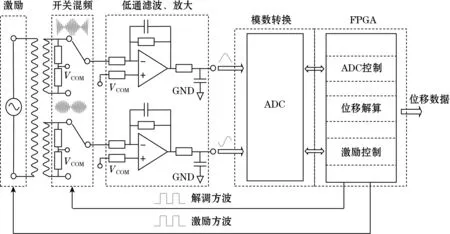
图2 传感器信号处理模块工作原理示意图

2 传感器的模型和仿真

为了验证传感器结构及其工作原理的可行性，用三维软件建立了如图1所示的传感器三维模型，并将其导入有限元仿真软件进行了电磁仿真，仿真参数如表1所示。

为了减少计算机的资源占用，只进行该传感器结构和原理可行性的定性分析，而不做定量计算。将仿真时间步长设置为0.02 μs，动尺起始位置为0，并以步长0.5 mm移动8 mm，每个位置仿真时间为0.5 μs。仿真结果如图3所示，感应线圈感应到的感应电动势波形是幅值随动尺位移变化而改变、相位不变的驻波。感应信号幅值随动尺位移的变化曲线如图4所示，表明当动尺在感应线圈Ci1、Ci2上移动一个结构周期，即8 mm时，Ci1、Ci2上的感应电动势V1、V2分别为

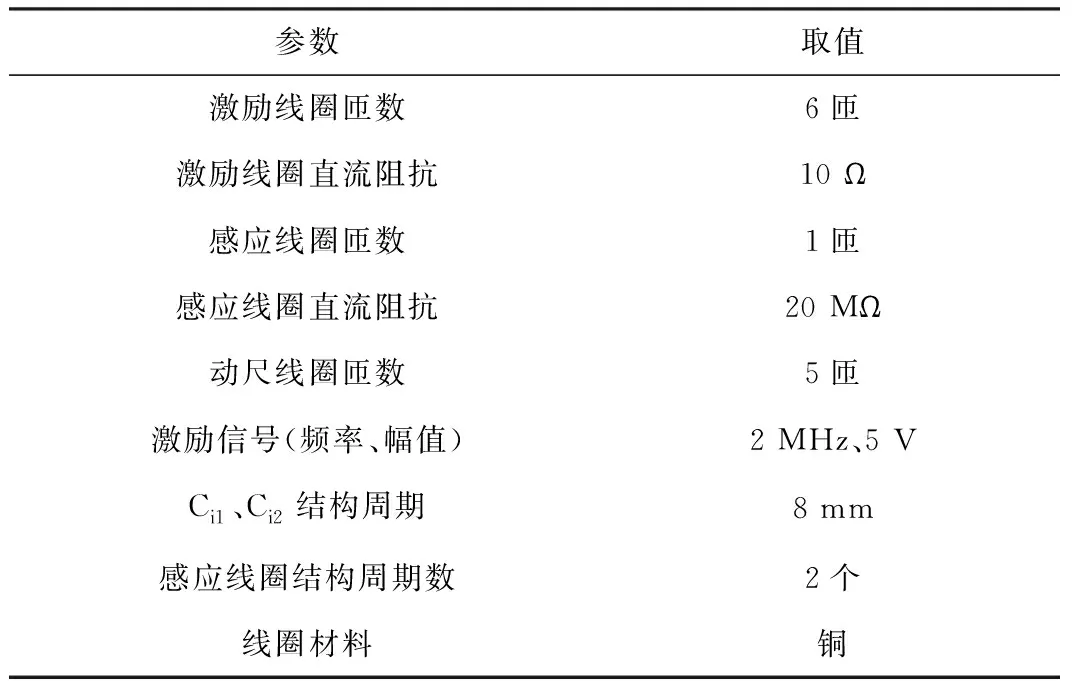
表1 传感器电磁仿真模型的主要参数设置

正弦、余弦信号。这正是前面推导的式(6)、式(7)对应的函数波形，表明仿真结果与理论相符，即验证了传感器结构和原理的可行性。

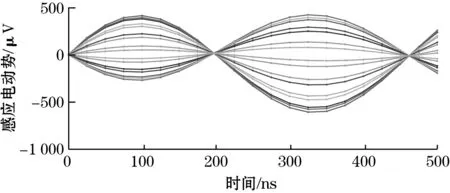
(a)感应线圈1的感应电动势

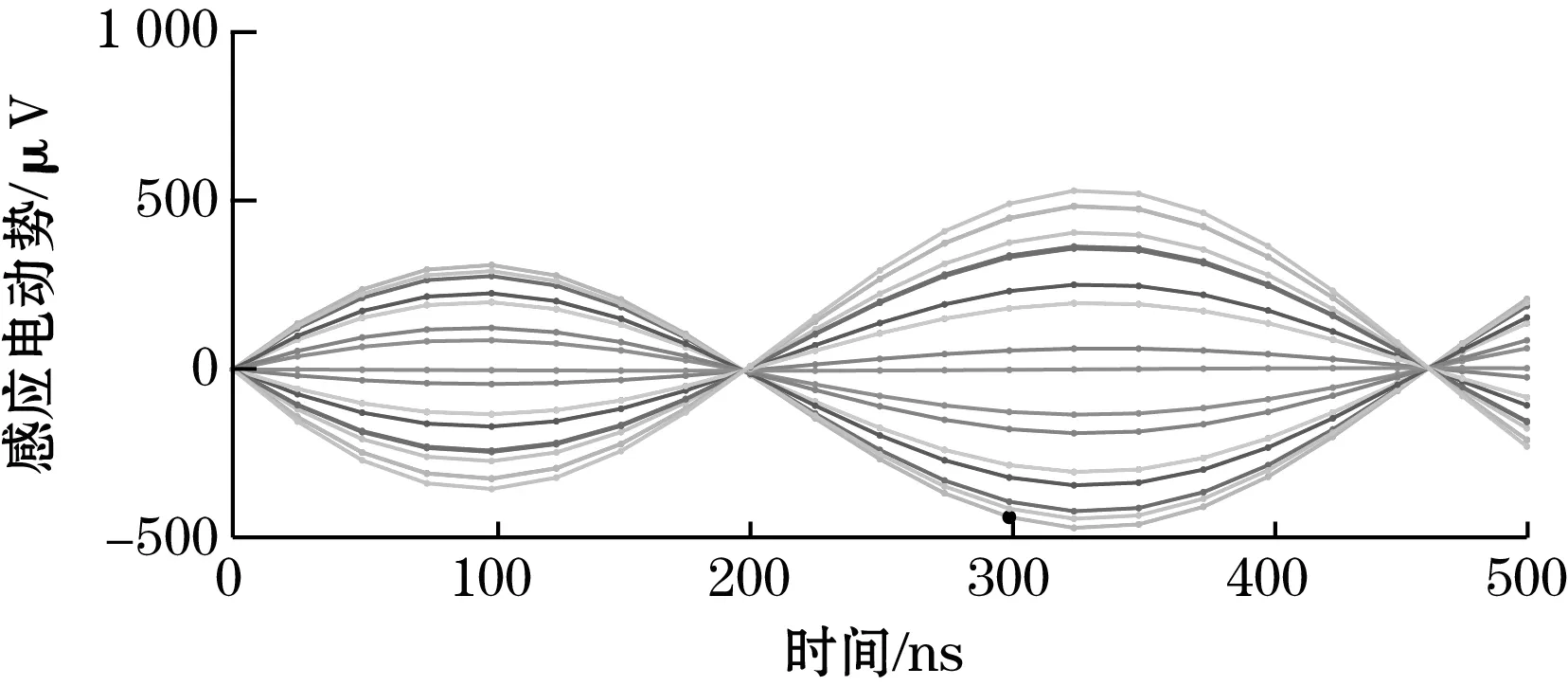
(b)感应线圈2的感应电动势图3 有限元电磁仿真原始曲线

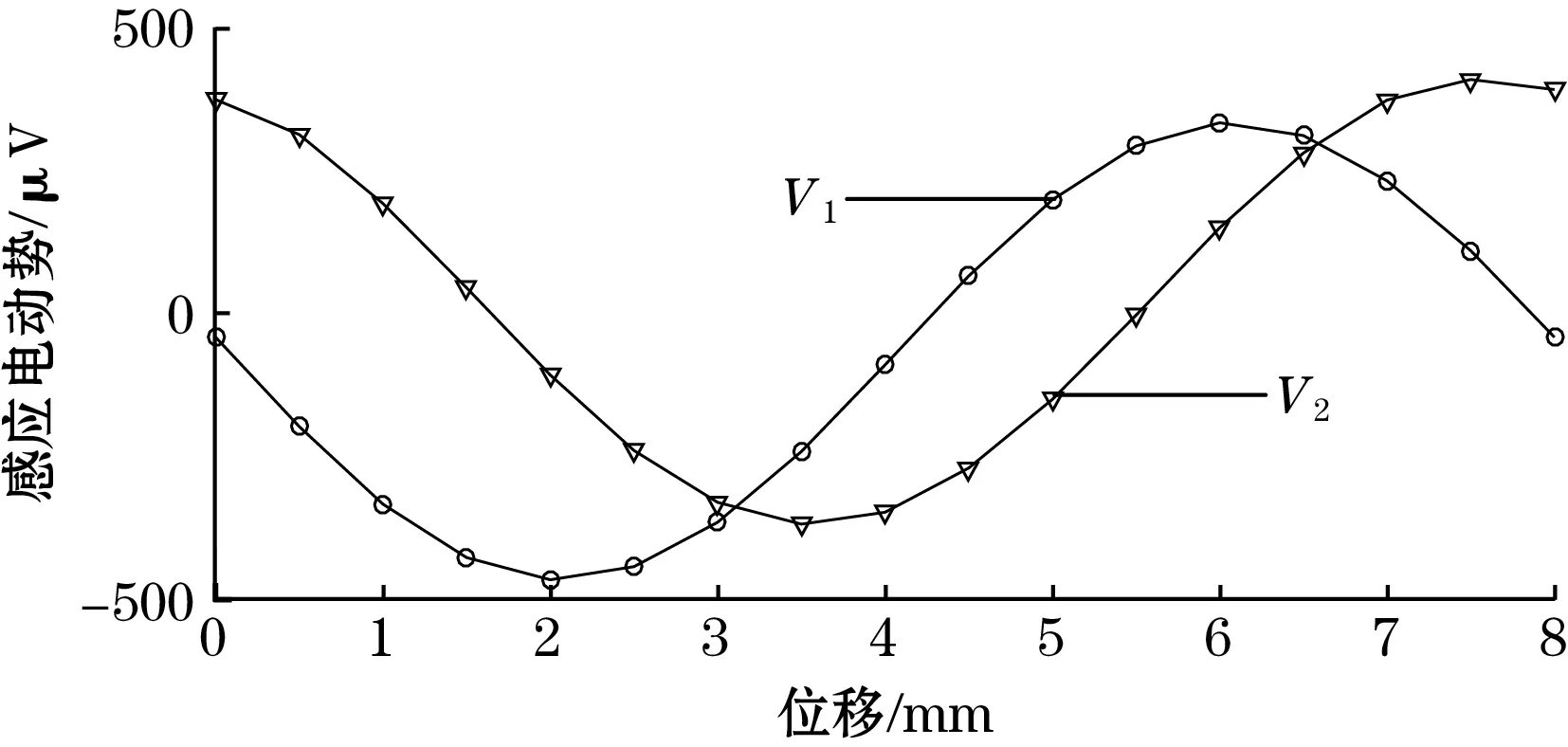
图4 感应电动势随动尺位移的变化

3 传感器样机与实验

由于PCB具有批量一致性高、便于批量生产、成本低、布线均匀等优点，很多电磁感应式位移传感器都采用PCB技术[15-16]。本文所研究的传感器样机也采用了PCB技术。将激励线圈和感应线圈印制在定尺PCB上，如图5(a)所示(另外一组感应线圈是为以后实现绝对式做准备)。动尺线圈印制在动尺PCB上，为了提高动尺线圈中的电流，使其产生更强的磁场，将动尺线圈与电容串联起来以产生串联谐振，如图5(b)所示。测试样机的实验平台如图6所示。动尺固定在3D打印的动尺基体上，动尺基体固定在导轨的运动部件上，定尺固定不动，并使2块动尺关于定尺平面对称，如图7所示。

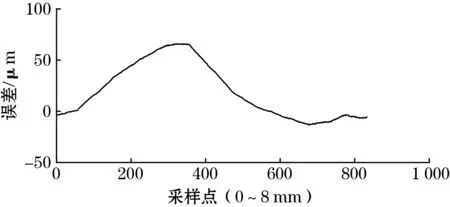
传感器样机的感应线圈结构周期长度与仿真相同，2块动尺与定尺的间隙均为0.8 mm。实验中，以光栅尺的位移为测量基准，检测传感器样机的位移测量误差。传感器样机在一个结构周期内的原始误差(短周期误差)峰峰值为79 μm，如图8(a)所示。

图5 动定尺实物图

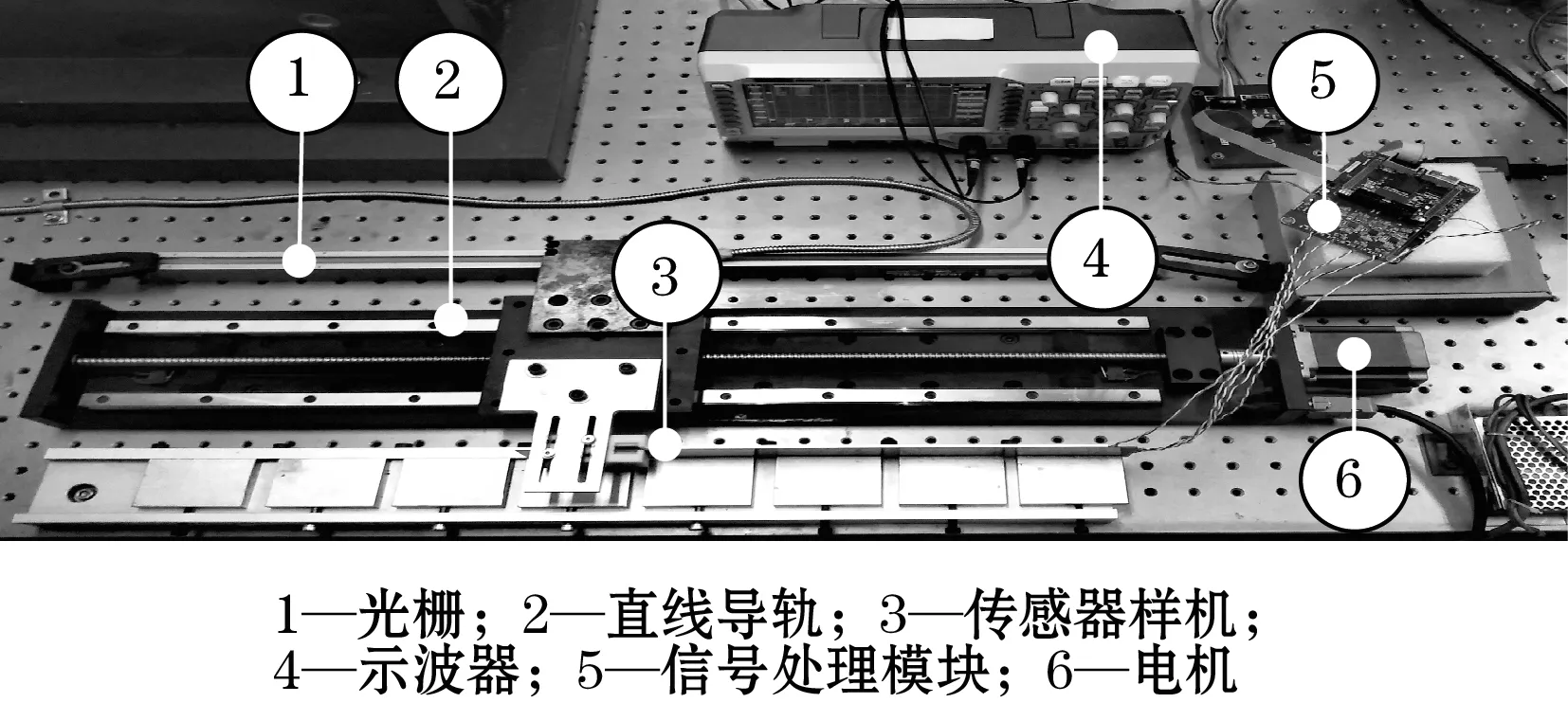
图6 传感器样机的实验平台

图7 动定尺实验安装图

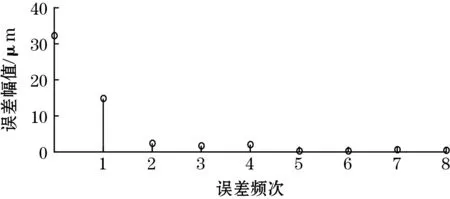
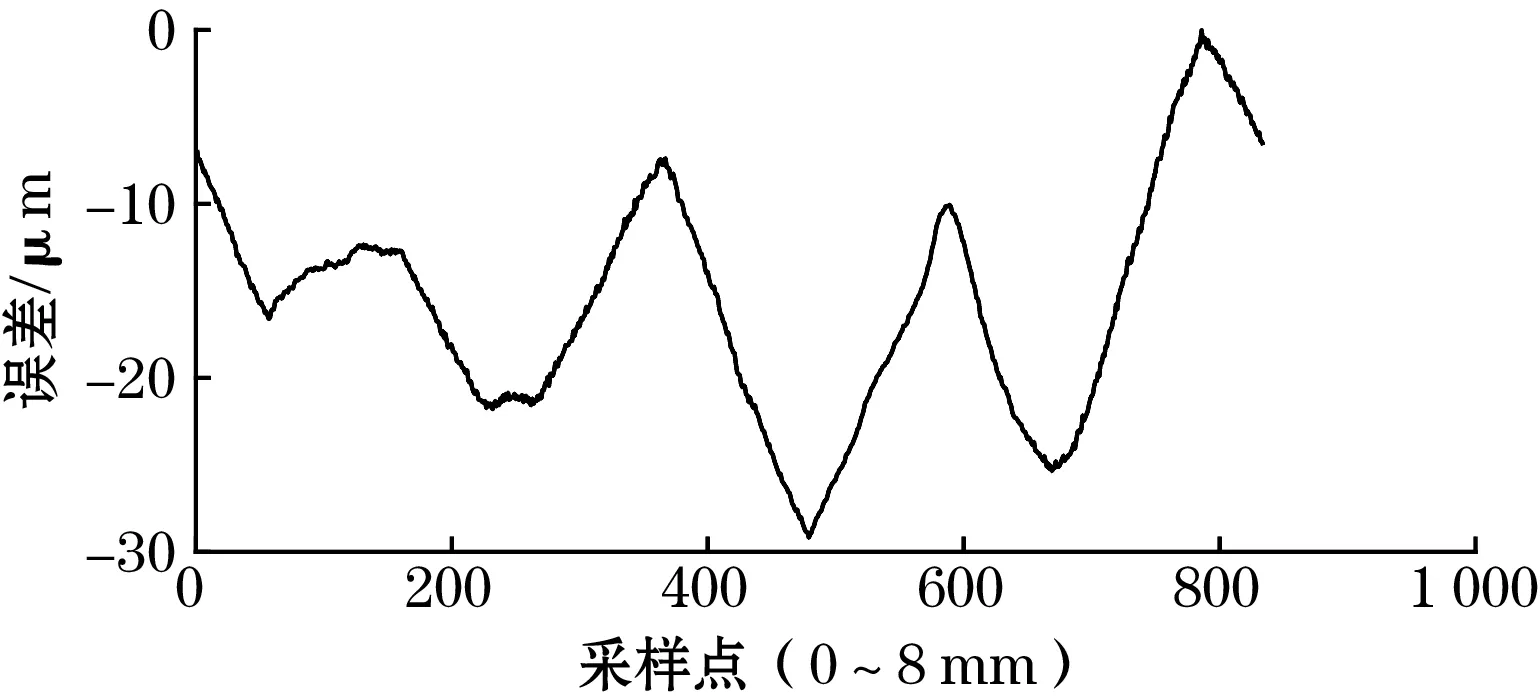
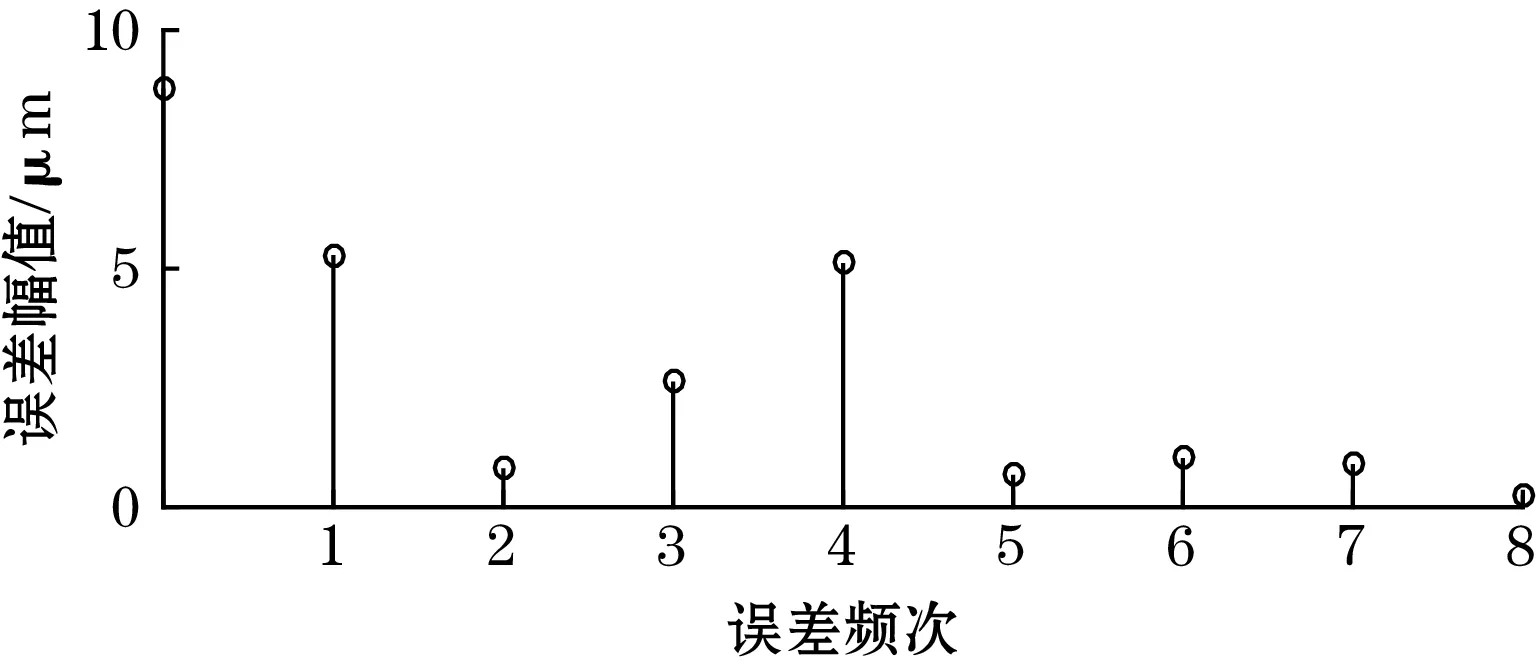
对该误差进行快速傅里叶变换(FFT)分析，得到如图8(b)所示的误差频次，从图8(b)可以看出，1次误差占主导，由文献[13]中的误差来源分析可知，该传感器的感应信号中具有较大的、与位移不相关的直流偏移量，这主要由激励信号中的噪声导致。为了减小噪声信号对传感器测量精度的影响，在激励部分使用了LC低通滤波器，使激励信号由原来频率为2 MHz的方波变为正弦波。再次测量，传感器的短周期误差峰峰值减小到29 μm，如图8(c)所示。再次FFT分析，得到如图8(d)所示的误差频次，其中4次误差占主导。根据文献[11]可知，减小结构周期长度或增加定尺与动尺的间隙，可以减小4次误差。考虑到传感器输出信号的信噪比，所以将感应线圈的周期长度减小至4 mm，重新设计并制造了定尺和动尺。不过，新样机的短周期误差减小并不明显，误差峰峰值为27 μm，如图8(e)所示。不同的是，此时的短周期误差成分发生了变化，如图8(f)所示，2次误差占主导。根据文献[13]中误差来源的分析，2次误差的产生与感应线圈没有严格空间正交(即相差1/4个结构周期)和正余弦感应信号幅值不等有关。因感应线圈在设计上已严格空间正交，但PCB制作环节可能会导致感应线圈没有严格空间正交且无法改变，故只能进行正余弦感应信号的幅值补偿，以减小二者幅值不等的影响。补偿幅值后，传感器样机的短周期误差显著减小，峰峰值为9 μm，如图8(g)所示。

(a)

(b)

(c)

(d)

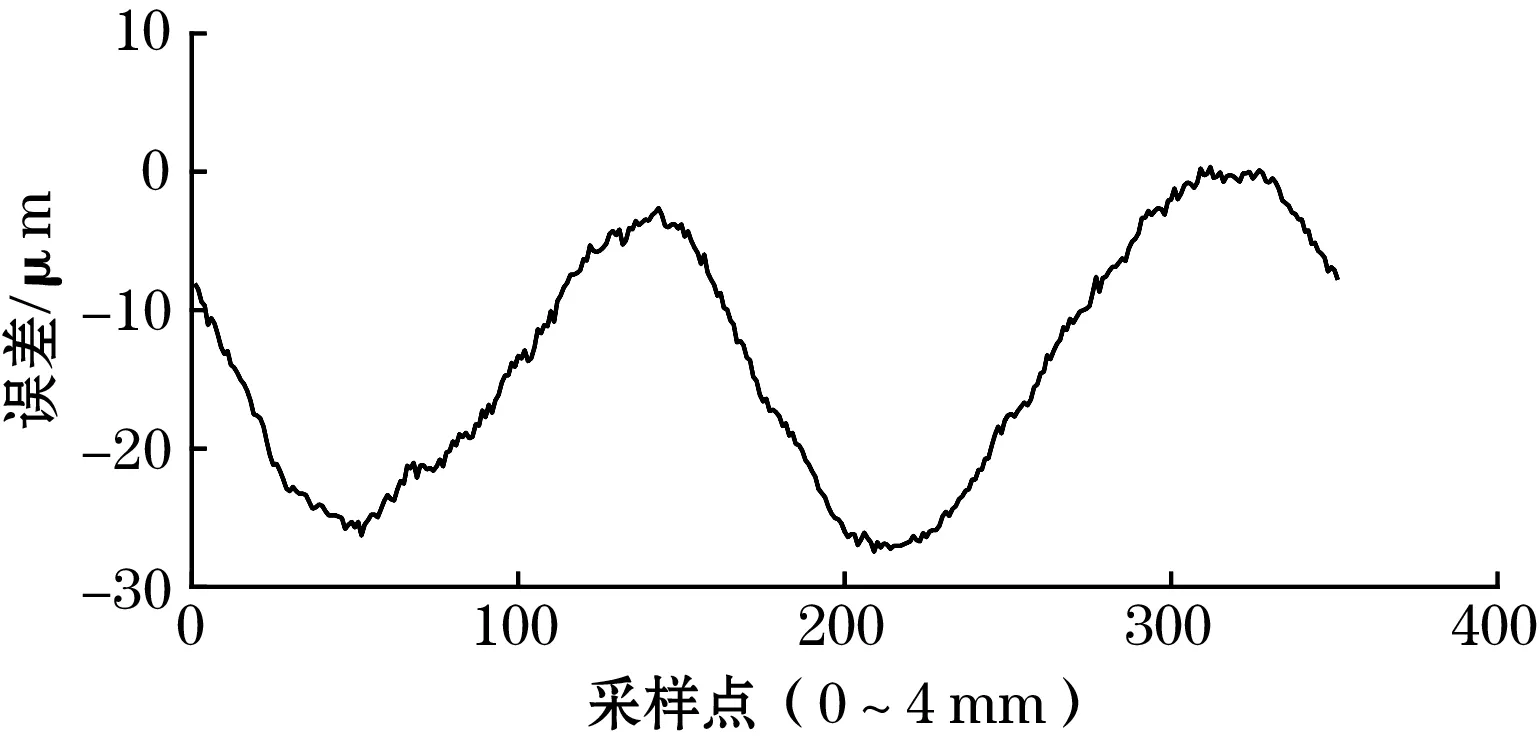
(e)

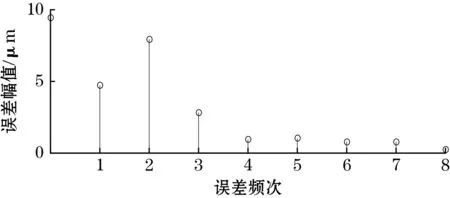
(f)

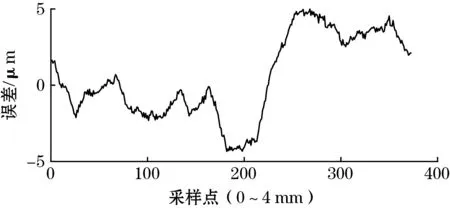
(g)图8 样机的短周期误差及误差频次

最后，进行了传感器样机长周期误差的测试。在300 mm的量程范围内，原始测量误差峰峰值为13 μm，误差曲线如图9所示。

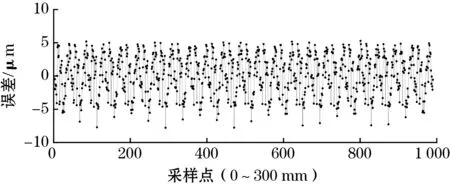
图9 样机的长周期误差

4 结束语

本文开展了一种互补谐振耦合型电磁式直线位移传感器研究。首先，对新型的传感器结构进行了介绍，并描述了其基本工作原理。然后，建立传感器的三维模型，并进行了电磁场有限元仿真，仿真验证了新型传感器结构和工作原理的可行性。最后，研制出传感器样机及其相应的信号处理电路，并完成了传感器的测试。测试实验表明，改进的传感器样机在一个周期内，原始测试误差峰峰值为9 μm，与文献[8]和文献[9]的传感器相比，测量精度分别提高了40%和91%。

该传感器借鉴和吸收了文献[8-10]所研究的传感器的优点。第一，在动尺无引线情况下，传感器可实现高精度位移测量；第二，动尺线圈采用谐振方式增强了感应信号，如同文献[10]；第三，采用与文献[8-9]类似的双边传感结构，增强了传感器对安装和使用问题的抑制能力。因此，通过对本文提出的传感器的进一步研究，有望能更好地发挥互补耦合型直线位移传感器的优势。