基于差分进化和聚类方法的入选原矿分类

周 冶 王庆凯 余 刚

(1.矿冶科技集团有限公司，北京102628；2.矿冶过程自动控制技术国家重点实验室，北京102628)

钽铌是耐高温、耐腐蚀、可塑性好的稀有金属，是国民经济和国防军工发展必不可少的重要原材料，目前钽铌广泛应用于电子、精密陶瓷和精密玻璃工业、电声光器件、硬质合金、生物医学工程、核工业、航天工业、超导工业、特种钢等产业[1]。钽铌选矿有自己的特点，钽铌矿多以伴生矿床为主，钽铌品位低，嵌布粒度细，矿物组成复杂，因此钽铌矿选矿多为多金属选矿，产品多且工艺流程复杂，选矿难度大[2]。

目前，我国经济发展进入新常态，去产能和供给侧改革成为国内众多生产制造企业的主旋律。全球矿山行业竞争加剧，新形势下越来越多的矿山企业认识到推进生产精细化、透明化，实现企业内外资源合理配置的迫切性与重要性。某钽铌矿是具有规模化采、选能力的大型钽铌矿山企业，是国内主要的钽铌、锂原料生产基地。经过几十年的开采，钽铌原矿品质整体在下降，钽铌选矿成本也不断提高。为了解不同入选原矿的选矿结果差异与变化趋势，更准确制定生产计划，合理进行生产调度，本文从钽铌选矿生产工艺流程考虑，进行物料平衡分析，运用差分进化算法分析计算每种原矿在各个生产环节中的物料变化情况，在此基础上结合聚类的方法对入选原矿进行分类。

进化算法(Evolutionary algorithms)是一类模拟自然界生物自然选择与自然进化的随机搜索算法，相较于传统方法在求解高度复杂的非线性问题上具有明显优势，且具有较好的通用性。选矿行业是典型的复杂流程工业，选矿过程伴随着物理变化和化学变化，过程机理复杂，具有多变量、非线性、大滞后和强耦合等特性[3]，进化算法也被广泛应用于选矿生产中。顾清华运用自适应的遗传算法求解基于采选流程的多金属多目标配矿优化数学模型，保证了矿石品位的均衡性以及矿石的可选性[4]；任宏阳运用改进的人工鱼群算法结合支持向量机回归原理对浮选精矿品位和回收率进行预测，为现场的实际操作提供指导，取得了较好的效果[5]。

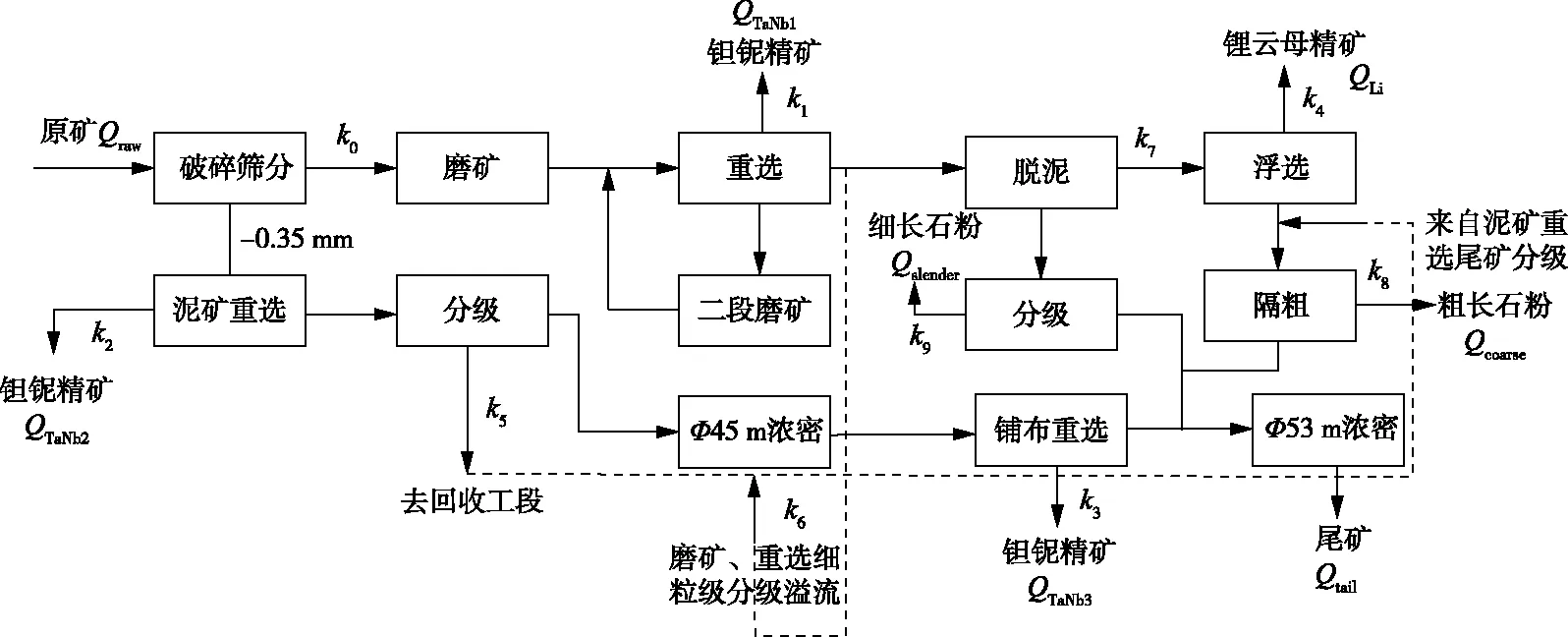
图1 选矿生产过程流程图Fig.1 Mineral processing flowsheet

1 最小化物料平衡误差目标模型

1.1 生产流程与物料平衡分析

钽铌矿选矿工艺复杂，选厂的产品主要为钽铌精矿、锂云母精矿和长石粉。选厂选矿生产分为破碎筛分、磨矿重选、综合回收三个工段，具体的选矿生产流程如图1所示。本研究中用物料变化系数k0、k1、k2、k3、k4、k5、k6、k7、k8和k9描述各个生产环节中的物料变化情况，每个系数都有实际的生产意义。k0是磨矿、重选入选比；k1是主厂房重选选矿比；k2是泥矿重选选矿比；k3是铺布钽铌精矿选矿比；k4是浮选选矿比；k5是重选尾矿分级进入回收工段的分级比；k6是主厂房重选尾矿中细粒级分级溢流比例；k7是重选尾矿脱泥比；k8是隔粗比；k9是细泥分级比。各个环节相关的指标与物料变化系数的理论推导关系见式(1～7)。

(1)

(2)

(3)

(4)

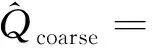
(1-k0)(1-k2)k5]k8Qraw

(5)

(6)

(1-k0)(1-k2)k5]Qraw+

[(1-k0)(1-k2)(1-k5)+

k0k6](1-k3)Qraw+

(1-k1-k6)(1-k7)(1-k9)k0Qraw

(7)

1.2 最小化物料平衡误差目标模型

在现有生产工艺下，各个环节中的物料变化系数是由原矿的性质决定的，根据生产报表原矿入选的物料变化系数k0、k1和k2可以直接计算。k3是由其余物料变化系数决定的，研究中需先确定其他物料变化系数，因此需要进一步研究计算的物料变化系数是k4、k5、k6、k7、k8和k9，传统的方程求解很难精准计算，本文采用进化算法寻找近似最优解。本文以k4、k5、k6、k7、k8和k9为决策变量，计算各产品的产量，将最小化每个理论产量与报表中的真实数据误差作为优化目标，即最小化物料平衡误差，建立目标模型见式(8)。

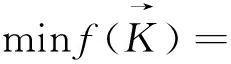
(8)

(9)

(10)

(11)

决策变量都是介于0和1之间的系数。此外，根据现场生产经验，铺布选矿流程的入选原矿主要来自于磨矿、重选细粒级溢流和泥矿重选尾矿，选矿难度最大，选矿比小于主厂房磨重工段的重选选矿比(具体见式(12～13))。

(12)

k4,k5,k6,k7,k8,k9∈[0,1]

(13)

根据生产工艺流程可知，细长石粉和锂云母精矿的总产量一定小于主厂房重选尾矿量，粗长石粉、细长石粉、锂云母精矿和尾矿的总量一定大于主厂房重选尾矿量，主厂房的钽铌精矿量远远小于锂云母精矿产量和长石粉产量(具体见式(14))，故可以忽略不计。

(14)

2 基于差分进化算法的物料变化系数计算

2.1 差分进化算法概述

差分进化算法(Differential evolution，简称DE)作为一种新型、高效的启发式并行搜索技术，是由Store和Price于1997年提出的一种基于群体差异的启发式并行搜索方法[6]，通过对现有优化方法进行大胆的扬弃，使其具有收敛快、控制参数少、设置简单、优化结果稳健等优点，对进化算法的理论和应用研究具有重要的学术意义[7]。

差分进化算法相对于遗传算法而言，相同点都是通过随机生成初始种群，以种群中每个个体的适应度值为选择标准，主要过程也都包括变异、交叉和选择三个步骤，具体的算法流程见图2。不同之处在于遗传算法是根据适应度值来控制父代杂交，变异后产生的子代被选择的概率值，在最大化问题中适应值大的个体被选择的概率相应也会大一些。而差分进化算法变异向量是由父代差分向量生成，并与父代个体向量交叉生成新个体向量，直接与其父代个体进行选择。相对于遗传算法，差分进化算法的逼近效果更加显著。

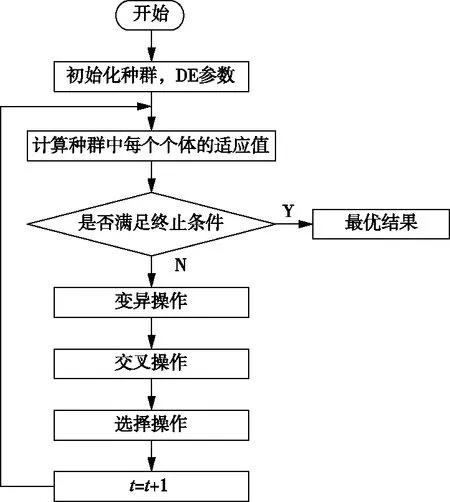
图2 差分进化算法流程Fig.2 Flowsheet of differential evolution algorithm

2.2 物料变化系数计算

本文研究中的实际生产数据以某种入选原矿在某生产周期内报表的统计为准。某入选原矿某段时间的相关生产指标数据汇总如表1所示。

表1 某周期内相关生产指标数据

结合表1中的数据，将其带入目标模型，使用差分进化算法进行物料变化系数的计算，并与传统经典遗传算法进行比较。模型的决策变量维数n为6，其中φ取0.05，遗传算法参数设置中，最大进化代数为100，种群规模M为50，变异概率为0.2，交叉概率CR为0.7；差分算法参数设置中，最大进化代数为100，种群规模M为50，缩放因子F为0.5，交叉概率CR为0.7；遗传算法与差分进化算法求解过程中种群个体平均目标值和种群最优个体目标值收敛情况如图3和图4所示。

图3 遗传算法进化过程种群个体目标值收敛情况Fig.3 Convergence of individual objective value in evolutionary process of GA

图4 差分进化过程种群个体目标值收敛情况Fig.4 Convergence of individual objective value in evolutionary process of DE

图3和图4对比可以看出，差分算法的表现明显优于传统遗传算法。差分进化最后一代种群中个体目标函数值接近0，标准差接近0，差分进化算法取得了较好的收敛性和稳定性，更为高效，40代左右就达到了最优。随机运算多次结果汇总如表2所示。

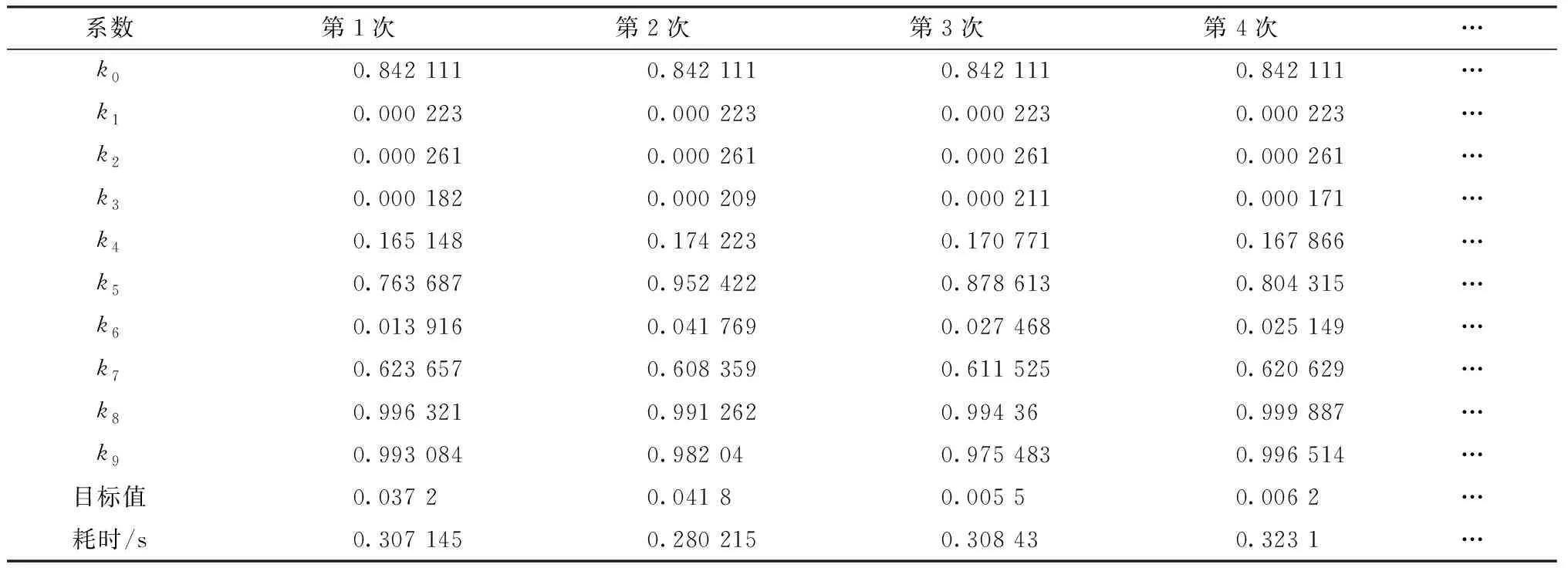
表2 随机运算多次数据结果

表2中每一次运算的目标值都接近0，即每一组都是一组最优解。所求物料变化系数中大多数系数都在很小的区间波动，只有系数k5在较大的范围波动，表2中系数k5最小值为0.763 687，最大值0.952 422，该系数表示泥矿入选尾矿分级进入回收工段生产粗长石粉的比例，矿石性质和各个环节人工作业对该系数的影响很大。系数波动的绝对区间越大，对分类结果影响越大，必须减少系数k5的波动对分类结果的影响，研究中将每种矿石的报表数据在该模型下求解100次，取100次求解结果中系数k5平均值，选取最接近k5平均值的一组求解结果作为该种矿石的物料变化系数。

将表1数据带入计算100次并算出物料变化系数k5平均值，求出系数k5的均值为0.843 823 2，全部输出结果按系数k5的均值误差从小到大进行排序，前5组数据汇总如表3所示，该入选原矿的物料变化系数即为第一组系数。重复以上方法计算已知14批入选原矿的物料变化系数，结果如表4所示。

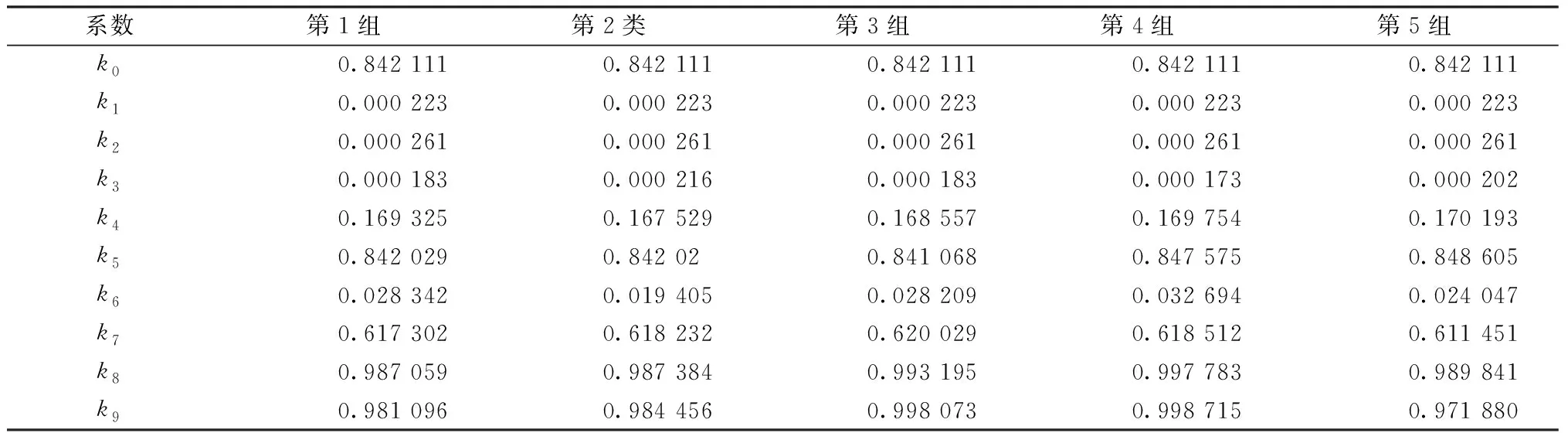
表3 结果排序前5组

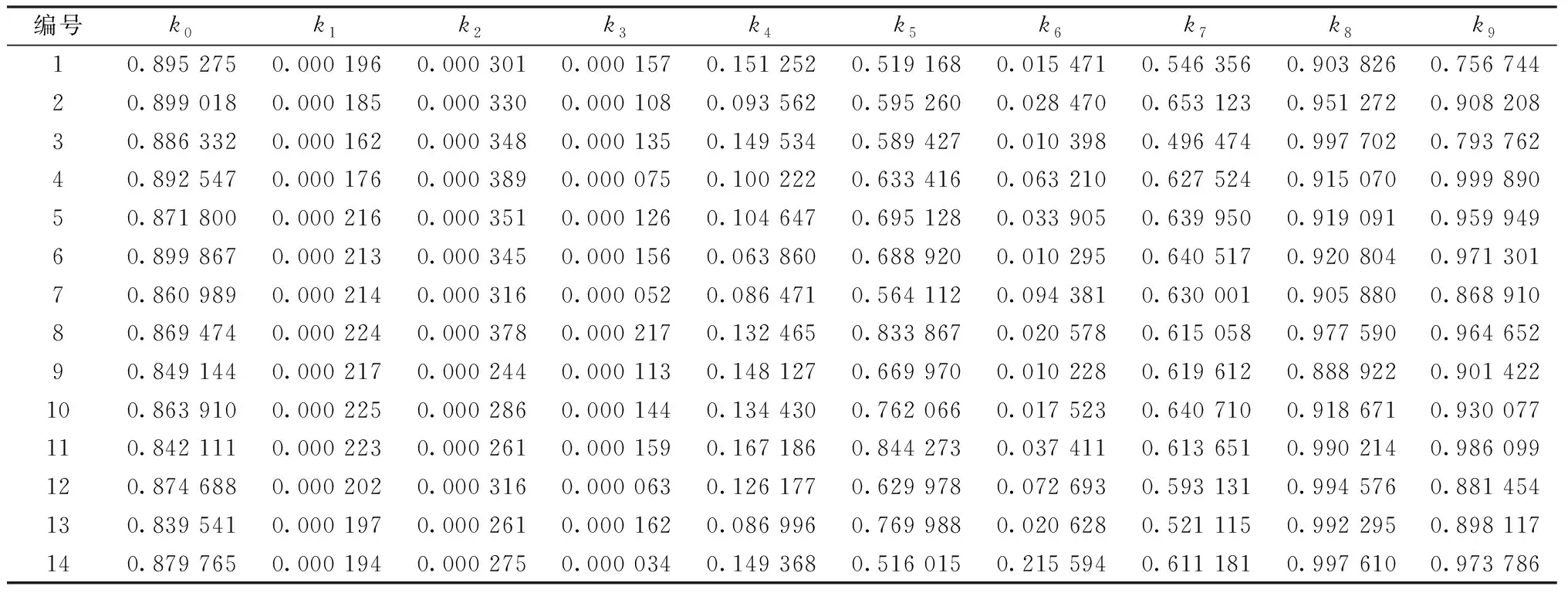
表4 14批入选原矿物料变化系数汇总

3 基于聚类方法的入选原矿分类

3.1 聚类方法和K-Means概述

聚类算法是经典的机器学习算法，有实用、简单和高效的特性。聚类过程为特征提取，根据数据之间相似度进行分簇，以达到同一簇中的数据对象相似度高、不同簇中的数据相似度低的目的。传统的聚类算法可分为：分区聚类、层次聚类、基于密度的聚类、基于模型的聚类和基于网格的聚类[8]。本文选取经典的K-Means算法进行原矿的分类研究。

K-Means是机器学习中最为经典和常用的聚类算法之一，是一种迭代求解的算法，通过样本点与聚类中心的距离衡量数据之间相似度，属于无监督算法[9]。K-Means是通过计算样本与聚类中心点之间的距离进行划分聚类。主要包含两层内容：初始中心点个数(计划聚类数)K和中心点到其他数据点距离的平均值means。先随机设置K个特征空间内的初始聚类中心，计算其他点到每个中心点的距离，最近的作为标记类别，然后重新计算每个类的新中心点，重复之前操作直至中心点不再变化。基于以上计算方法通过入选原矿的物料变化系数对原矿进行分类，本文中使用欧式距离度量，即n维空间内点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)之间的距离，其关系见式(15)。

(15)

K-Means聚类中需要注意的就是常数K的确定，即分多少类可以使用轮廓系数法确定最合理的K值。轮廓系数的计算方法见式(16)。

(16)

公式(16)中ai是样本i在同类别内到其它点的平均距离，bi是样本i到最近不同类别中样本的平均距离。平均轮廓系数的取值范围为[-1,1]，系数越大，聚类效果越好。簇内样本的距离越近，簇间样本距离越远。

3.2 原矿分类计算

研究中采用K-Means方法对物料变化系数进行分类，从而对原矿种类进行区分。轮廓系数法可以很好地确定合适的类别数，平均轮廓系数的取值范围为[-1,1]。类别数为1类或者14类就没有意义，类别过少会受到异常点的影响，类别过大会造成样本均衡问题。类别数最少为2类，最多为13类，这里将所有可能的类别数进行轮廓系数法循环计算。全部可能的类别数下的轮廓系数计算汇总如表5所示。

表5 不同类别数的平均轮廓系数

从表5可以看出，当类别数K为5时，平均轮廓系数(Average silhouette score)约等于0.339，是所有分类可能中的最大值。将表4中所有种类原矿的物料变化系数的汇总数据进行标准化处理，使用python的sklearn库可以迅速调用K-Means方法将所有入选原矿进行分类，分类结果如表6。

表6 分类结果

3.3 分类后物料变化系数计算

前面的研究工作中运用K-Means方法将原矿分为5类，分类后每一类入选原矿的物料变化系数需要重新确定。其中第3类的入选原矿只有一种原矿，其物料变化系数由所属的第14种原矿确定，不需要重新确定。其余类别的原矿物料变化系数求解的问题模型建立在1.2节中模型的基础上。假设其中某类所属原矿种类的集合为A，该模型的优化目标是最小化全部所属种类原矿在同一物料变化系数下的理论值与报表数据的误差和，即：

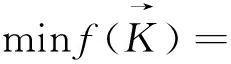
(17)

式中，

公式(17)中λi、λ1,i、λ2,i和λ3,i是放缩系数，Qk是常数，A是当前类别下所属原矿种类的集合。该类别下物料变化系数中k0、k1、k2、k3取全部所属种类原矿相应系数的平均值，决策变量仍然是k4、k5、k6、k7、k8、k9，约束条件则是该类别下每种原矿在同一物料变化系数下的理论值与报表数据的误差不超过φ。

对于任意i∈A，则有

(18)

(19)

(20)

决策变量都是介于0和1之间的系数，铺布选矿的入选原矿主要来自于磨重细粒级溢流和重选尾矿，选矿难度最大，选矿比小于主厂房磨重工段的重选选矿比(见式(22))。

k4,k5,k6,k7,k8,k9∈[0,1]

(21)

(22)

其中Qk设置为5 000，φ取0.05。再次沿用差分进化算法对分类后各类别原矿的物料变化系数求解，模型的维数n为6，差分算法设置最大进化代数为100，种群规模M为50，缩放因子F设置为0.5，交叉概率CR设置为0.7。在该模型下运算100次，取100次结果中系数k5平均值，选取系数k5最接近平均值的一组求解结果作为该种矿石的物料变化系数，最终确定所有类别原矿的物料变化系数，汇总如表7。

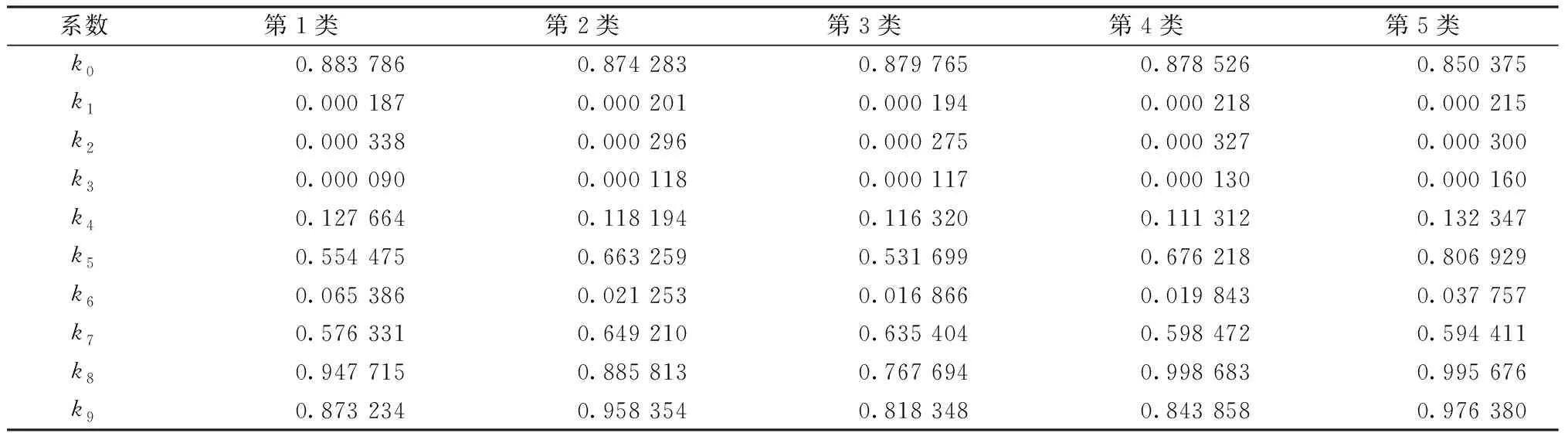
表7 各类别原矿物料变化分析系数

4 结论

为了更好了解不同批次入选原矿的情况，本文针对钽铌选厂不同入选原矿的选矿结果差异开展了入选原矿的分类研究。首先结合实际生产工艺流程开展物料与金属平衡分析，研究各个生产环节中的物料变化情况；然后以最小化物料平衡误差为目标建立求解各个环节物料变化系数的数学模型。对比传统经典遗传算法，差分进化算法明显具有更好的收敛性与稳定性；运用差分算法多次运算确定合适的物料变化系数，以物料变化系数作为分类指标，结合K-Means方法进行分类，再运用差分进化算法确定合理的各个类别的物料变化系数。通过对入选原矿的分类，调度人员可以很好地了解入选原矿的变化趋势，为制定采选生产计划、进行合理地生产调度提供参考。