超重力反应器内MEA-乙醇溶液用于沼气脱碳的优化传质模型

尹龙天， 李秀金， 张 良*， 常燕青

(1.北京化工大学 化学工程学院， 北京 100029； 2.维尔利环保科技集团股份有限公司， 江苏 常州 213125)

MEA溶液化学吸收法脱除CO2具有脱碳程度高、操作压力低等优点，因而获得了广泛的研究与应用[1-3]。近年来超重力反应器用于MEA化学吸收法脱碳进一步降低了溶液循环量和投资成本，有着极大的研究与应用前景[4-6]。而以乙醇代替水为MEA溶剂的MEA-乙醇溶液在吸收性能方面与MEA-水溶液相当，解吸性能方面远远优于MEA-水溶液，也具有很大的研究与应用潜力[7-8]。

超重力反应器是一种过程强化设备，通过转子的高速旋转可以使超重力反应器产生比重力强数百倍的离心力场，反应器中的流体在离心力场中可以被切割为液滴、液丝等微米级的微小颗粒，极大的增加了传质面积、提高了传质效率。超重力反应器一般为逆流式，其结构包括壳体、转子、填料、电机等[9-10]。

但目前超重力反应器与MEA-乙醇溶液化学吸收法结合用于脱碳的研究主要集中在低含量CO2脱除，而且多为实验研究，理论及模型研究还相对较少，关于沼气脱碳这种典型的高含量CO2脱除的模型研究更是几乎没有。MEA用于沼气脱碳是伴随化学反应的高含量气体吸收过程，传质过程中气相流量会产生较大变化，而且MEA与CO2的反应热较高，传质过程中的气液相温度也会产生较大变化，使传质过程变得极为复杂。传质模型的建立能够为工业设计提供指导，具有极为重要的意义，这方面的研究亟待加强。

针对上述问题，本文建立了超重力反应器内的MEA-乙醇溶液脱除沼气中高浓度CO2的传质数学模型，利用改进的气液平衡常数来描述化学反应过程；通过双膜理论建立了传质数学模型和描述反应器内气液温度变化的传热数学模型；通过模型预测传质结果，并与实验值进行对比分析，进一步对模型进行优化。

1 实验部分

本研究的实验分为MEA-乙醇溶液对CO2吸收能力测定实验和超重力反应器内MEA-乙醇溶液用于沼气脱碳的传质实验。

1.1 实验材料

沼气采用CH4高压钢瓶气与CO2高压钢瓶气配制而成，纯度为99.99%。MEA-乙醇溶液采用分析纯MEA与分析纯无水乙醇配制。

1.2 实验系统

MEA-乙醇溶液对CO2吸收能力测定实验的实验系统流程如图1所示，将装有一定量溶液的三口烧瓶置于天平上，向溶液中鼓入CO2，记录天平的示数变化，待示数稳定后计算溶液对CO2的吸收能力。

1.CO2钢瓶； 2.减压阀； 3.浮子流量计； 4.天平； 5.三口烧瓶； 6.温度计； 7.蛇形冷凝管； 8.尾气吸收

超重力反应器内MEA-乙醇溶液沼气脱碳的实验系统流程如图2所示，CO2和CH4的钢瓶气通过调节阀进行流量调节，配制成一定CO2浓度的沼气，经过稳压罐流入反应器(超重力反应器填料层参数见表1)。使用泵将MEA-乙醇溶液由贫液罐打入超重力反应器中，与沼气进行逆流接触传质，完成传质的富液储存在富液罐中，气体流入在沼气分析仪测定成分。

1.CO2钢瓶； 2.CH4钢瓶； 3.CO2浮子流量计； 4.CH4浮子流量计； 5.稳压罐； 6.进气流量计； 7.变频电机； 8.超重力反应器； 9.富液罐； 10.贫液罐； 11.柱塞计量泵； 12.进液流量计； 13.沼气分析仪

表1 超重力反应器填料层参数

1.3 实验设计

CO2吸收能力测定实验旨在确定MEA-乙醇溶液的吸收能力，为建立模型提供基础数据。固定CO2鼓入速率，分别测定MEA质量分数为10%、20%、30%的溶液的吸收能力，吸收能力通过饱和溶液的CO2负荷(单位摩尔量MEA吸收CO2的摩尔量，mol CO2·mol-1MEA)来评价。

超重力反应器内的传质实验旨在收集实验数据检测数学模型的可靠性。实验中的沼气成分为50%CH4、50%CO2，MEA-乙醇溶液浓度为4.92 mol·L-1。实验参数设计见表2。

表2 实验参数设计

1.4 实验结果与讨论

CO2吸收能力测定的实验结果如图3所示，传质实验的实验结果如图4～图6所示。

不同MEA浓度吸收剂的CO2吸收能力如图3所示，可见随着MEA浓度的上升富液负荷有所下降，这主要是由于吸收剂粘度增加而导致的。

图3 CO2吸收能力随MEA浓度的变化

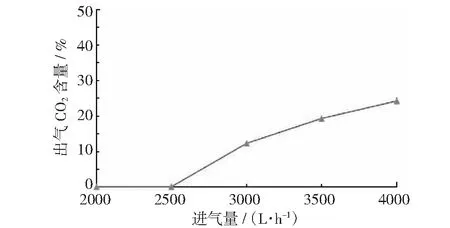
图4 不同进气量下的传质结果

图5 不同进液量下的传质结果

进气量、进液量、转子转速对传质的影响如图4～图6所示，可见出气CO2含量随进气量的升高而升高，随进液量的升高而降低，随转速的升高则是先变化不大，进而降低，最终稳定。

图6 不同超重力反应器转子转速下的传质结果

2 模型部分

2.1 模型假设

(1)根据相关文献资料[11-12]，超重力反应器内的大部分液体以液膜的形式存在；

(2)液体流动过程中没有轴向和径向上的返混；

(3)忽略端效应的影响；

(4)对填料微元，气液相流量为常量；

(5)对填料微元，传质系数为常量；

2.2 数学模型的建立

2.2.1 传质过程的数学模型

取超重力反应器填料层的填料微元作为研究对象，研究对象如图7所示。

L.液相流； G.气相流； r.微元环外半径； dr.微元环半径差

对于上述填料微元，其传质面积A可用公式(1)表示。

A=aeπ[r2-(r-dr)2]h

(1)

式中：A为填料微元传质面积，m2；ae为有效传质比表面积，m2·m-3；h为填料层高度，m，本研究为0.05 m；

传质面积表达式可简化为公式(2)。

A=2aehπrdr

(2)

填料微元内的单位时间传质通量Na以公式(3)表示。

Na=Gdy=Ldx=2JAaehπrdr

(3)

式中：Na为填料微元内单位时间的传质通量，kmol·s-1；G、L分别为气、液相流量，kmol·s-1；JA为局部传质速率，kmol·m-2s-1；x、y分别为液、气相摩尔分数，%。

局部传质速率JA计算式以公式(4)表示。

JA=Ky(y-ye)=Kx(xe-x)

(4)

式中：Kx、Ky分别为液、气相总传质系数(推动力以摩尔分数差表示)， kmol·m-2s-1；xe、ye分别为液、气相平衡摩尔分数，%。

对填料微元进行物料衡算，可得公式(5)。

G(y-yo)=L(x-xi)

(5)

联立公式(3)和式(4)引入气液平衡关系并积分，结合公式(5)可得公式(6)。

(6)

式中：xi、xo分别为流入、流出填料微元的液相溶质摩尔分数，%；yi、yo分别表示流入、流出填料微元的气相溶质摩尔分数，%；m表示气液平衡关系。

以上各式中的ae为有效传质比表面积，根据文献资料[13]，以公式(7)计算。

(7)

式中：dp为填料名义尺寸，dp=6(1-ε)/ap,m；φ为不锈钢丝网的丝径，mm；d0为不锈钢丝网的孔径，mm；νG为气体的运动粘度，m2·s-1；νL为液体的运动粘度， m2·s-1；ρL为液体密度，kg·m-3；ω为超重力反应器转子旋转的角速度，1·s-1。

本研究通过气液平衡关系来描述化学反应带来的影响，气液平衡关系可以理解为气体在液体中的溶解能力，通过前文CO2吸收能力测定实验的结果来确定气液平衡常数。

对于质量分数为w的MEA-乙醇溶液，其摩尔浓度可以用公式(8)表示、摩尔分数可以用公式(9)表示。

(8)

(9)

式中：MMEA、Methanol分别为MEA、乙醇的摩尔质量，g·mol-1；ρMEA、ρethanol分别为MEA、乙醇的密度，g·L-1。

CO2饱和的MEA-乙醇溶液的CO2负荷D(mol CO2·mol-1MEA)反映了溶液对CO2的溶解度，CO2摩尔分数与MEA摩尔分数的关系如公式(10)所示。

XCO2=DxMEA

(10)

在本研究的实验条件下，气相CO2摩尔分数为1，所以平衡常数的表达式为公式(11)。

(11)

根据吸收能力测定实验的实验结果可以由MEA-乙醇溶液的浓度确定饱和富液负荷D，进一步可以确定平衡常数。

由费克第二定律推导出CO2在液膜中的质量守恒式，如公式(12)。

(12)

式中：DL为CO2在溶液中的扩散系数，m2·s-1；c为液膜中CO2的摩尔浓度，mol·L-1；t0为扩散时间，s：rA为CO2的消耗速率(即MEA与CO2的反应速率)，kmol·m-3s-1；z为扩散距离，m。

双膜理论认为分子扩散为稳态，即浓度随时间是没有变化的，所以式(12)可写作公式(13)。

(13)

式中：k1为MEA与CO2的反应速率常数，m3·kmol-1s-1；cMEA为液膜中MEA的摩尔浓度，mol·L-1。

由双膜理论可知，传质发生在液膜中，气液界面浓度为ci，液相主体浓度为c，且不发生传质，无浓度梯度，设液膜厚度为δ(m)，那么公式(13)的积分边界条件为：

(13)

液膜内的局部传质速率定义式为公式(14)：

(14)

对公式(13)进行积分并联立公式(14)，可得液相传质系数表达式公式(15)：

(15)

根据文献资料[14-15]，k1通过公式(16)计算，液膜厚度通过公式(17)计算：

(16)

(17)

式中：T为液相温度，℃；Lv为液相流速，m·s-1。

根据文献资料，采用Onda等[16]提出的关联式计算气相传质系数，关联式如公式(18)。

(18)

式中：t为气相温度，℃；ap为填料比表面积，1·m-1；DG为CO2在气相中扩散系数，m2·s-1；μG为气体粘度，Pa·s；ρG为气体密度，kg·m-3；Gm为气相质量流速，kg·m-2s-1。

总传质系数用公式(19)表示。

(19)

式中：气液平衡关系H由公式(20)求取。

(20)

CO2在气、液相中的扩散系数由公式(21)计算。

(21)

式中：MA、MB分别为组分A、B的分子量，g·mol-1；VA为CO2的摩尔体积，cm3·mol-1；TCA、TCB为组分A、B的临界温度，K；VCA、VCB为组分A、B的临界容积，cm3·mol-1。

2.2.2 传热过程的数学模型

本研究中的传质过程为高浓度CO2的脱除，MEA吸收CO2产生的反应热较高，会带来气液相较为明显的温升，传质模型中的许多参数都与温度有着密切的关系，因此建立传热过程的数学模型非常重要。

传质过程中，MEA与CO2的反应热先造成溶液的升温，进而将热量传递给气体，因此传热的方向非常明确，是液相传递到气相。

传热过程中，假设气液界面温度等于液相温度，那么传热速率可以由公式(22)计算。

q=α(T-t)

(22)

式中：q为传热速率，kW·m-2；α为气相对流给热系数，kW·m-2℃；

以0 ℃作为焓的基本状态，那么气体的焓I可以由公式(23)计算。

I=Cgt

(23)

式中：Cg为气体比热容，kJ·kg-1℃。

上述内容为传热模型中的基本参数。仍以填料微元为研究对象，填料微元中的溶液蒸发量可以忽略，气液相流量看作恒定，第n层填料微元的热量衡算可以用公式(24)表示。

G(In-In-1)=LC1(Tn-Tn-1)

(24)

式中：Cl为液体比热容，kJ·kg-1℃。

热量衡算微分方程式为公式(25)。

GCgdt=α(T-t)2aehπrdr

(25)

将上述式子积分，可以得到传热过程的数学模型：热量衡算式为公式(24)，传热速率式为公式(26)。

(26)

2.2.3 数学模型的计算

将超重力反应器填料层径向等分100份，由填料内沿至外沿为第1到第100层，利用前文建立的填料微元模型从第1层逐层开始进行计算，第1层的有关未知参数先使用试差法进行赋值，算到第100层填料得到入口处的操作参数值，与实际操作值比较，如不同则重新赋值，直至得到的参数值与实际值相近。在固定沼气成分为50%CH4、50%CO2，溶液MEA浓度4.92 mol·L-1的条件下，利用上述计算方法分别对不同进气量、进液量和超重力反应器转速的传质结果(产品气CO2含量)进行预测。

2.3 模型的验证与改进

通过前文传质实验的实验结果对模型预测值进行验证，在进液量50 L·h-1、超重力反应器转速1000 r·min-1的条件下，不同进气量下的模型预测值与实验值的对比如图8所示。可见模型预测值与实验值较为吻合。

图8 不同进气量的模型预测值与实验值对比

在进气量4000 L·h-1、超重力反应器转速1000 r·min-1的条件下，不同进液量下的模型预测值与实验值的对比如图9所示。可见模型预测值与实验值非常接近。

图9 不同进液量的模型预测值与实验值对比

在进气量4000 L·h-1、进液量50 L·h-1的条件下，不同超重力反应器转速的模型预测值与实验值的对比如图10所示。可见转子转速的改变对模型结果基本没有影响，这是不符合实际的，说明本模型还存在一些问题。

图10 不同转速的模型预测值与实验值对比

针对模型出现的问题，对影响模型参数的因素进行分析，各模型参数的影响因素见表4。

表4 各模型参数对应的影响因素

模型参数中受转速影响的有超重力反应器传热速率、总传质系数、有效传质表面积、气体扩散系数、液膜厚度、MEA-CO2反应速率常数。但直接受转速影响的仅有效传质表面积和液膜厚度。根据相平衡常数，本过程属气膜控制的传质，液相传质系数的影响可以忽略，而液膜厚度主要影响液相传质系数，因此能影响到传质结果且受反应器转速影响的模型参数仅有效传质表面积。

根据前文的实验研究，超重力反应器转速对传质结果的影响是阶段性的，由实验数据可以看出，分界点在600、1000 r·min-1。低于600 r·min-1时传质结果较差且变化不大，高于1000 r·min-1时传质结果较好且变化不大。双曲正切函数可以正确地描述此现象，双曲正切函数(tanhx)的表达式如公式(27)所示。

(27)

其函数图像如图11所示，函数的值域为(-1,1)。

图11 双曲正切函数图像

引入双曲正切函数后的有效传质表面积表达式为公式(28)。

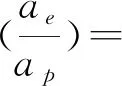
(28)

式中：dp为填料名义尺寸，dp=6(1-ε)/ap，m；φ为不锈钢丝网的丝径，mm；d0为不锈钢丝网的孔径，mm；νG为气体的运动粘度，m2·s-1；νL为液体的运动粘度，m2·s-1；ρL为液体密度，kg·m-3；ω为超重力反应器转子旋转的角速度，1·s-1。

利用修正后的模型重新进行计算，预测值与实验值的对比如图12所示。

图12 不同转速的修正模型预测值与实验值对比

修正模型预测值与实验值的整体对比如图13所示，可见本文建立的模型的预测值与实际值误差在15%以内。

图13 实验值与修正模型计算值的比较

3 结论

本文依据双膜理论建立了超重力反应器内MEA-乙醇溶液用于高含量CO2脱除传质过程的数学模型，以气液平衡常数来描述传质过程中发生的化学反应对传质带来的影响；并引入双曲正切函数对有效传质比表面积的关联式进行了优化。利用该模型对MEA-乙醇溶液在超重力反应器内用于沼气脱碳的脱碳效果进行了预测，通过实验结果验证了模型的预测值，发现模型值与实验值之间的误差在±15%以内，说明优化传质模型可以有效地预测传质结果，可以在一定程度上为工程设计起到指导作用。